Estructuras de acero: Problemas1 Clasificación de secciones
Anuncio

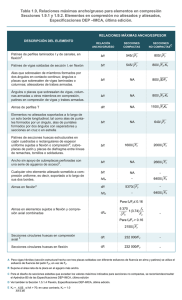
Estructuras de acero: Problemas1 Clasificación de secciones 1. Sección sometida a compresión: IPE 600 S-355 Datos fy = 355 N/mm2 ε = 235 fy = 0,81 h = 600 mm b = 220 mm tf = 19 mm tw = 12 mm r = 24 mm Clasificación del ala c = 0,5 ⋅ b = 110 mm c 110 = = 5,8 < 10 ⋅ ε = 8,1 → Clase 1 tf 19 1 tabla 5.4 Elementos Estructurales. Tomo 9. (1999). Instituto Técnico de la Estructura en Acero. San Sebastián Estructuras de acero. Problemas. Secciones. 1 Clasificación del alma d = h − 2 ⋅ t f − 2 ⋅ r = 600 − 2 ⋅ 19 − 2 ⋅ 24 = 514 mm c = d = 514 mm c 514 = = 42,8 > 42 ⋅ ε = 34,0 → Clase 4 tw 12 tabla 5.3 Por tanto, la sección es de Clase 4 2. Sección sometida a compresión: HEA 500 S-235 Datos fy = 235 N/mm2 ε = 235 fy =1 h = 490 mm b = 300 mm tf = 23 mm tw = 12 mm r = 27 mm Clasificación del ala c = 0,5 ⋅ b = 150 mm c 150 = = 6,5 < 10 ⋅ ε = 10 → Clase 1 tf 23 Estructuras de acero. Problemas. Secciones. tabla 5.4 2 Clasificación del alma d = h − 2 ⋅ t f − 2 ⋅ r = 490 − 2 ⋅ 23 − 2 ⋅ 27 = 390 mm c = d = 390 mm c 390 = = 32,5 < 33 ⋅ ε = 33 → Clase 1 tw 12 tabla 5.3 Por tanto, la sección es de Clase 1 3. Sección sometida a flexión: HEA 500 S-235 Se consideran dos casos distintos: a) Flexión por el eje y-y Las alas están sometidas a compresión o tracción uniforme, por lo que se clasifican así: c = 0,5 ⋅ b = 150 mm c 150 = = 6,5 ≤ 10 ⋅ ε = 10 → Clase 1 tf 23 tabla 5.4 El alma está sometida a flexión. Su clasificación es: c = d = 390 mm c 390 = = 32,5 ≤ 72 ⋅ ε = 72 → Clase 1 tw 12 tabla 5.3 Respecto a este eje, la sección es de Clase 1. b) Flexión por el eje z-z En principio, se supone que la sección está completamente plastificada en flexión pura. En este caso, las alas están sometidas a tensiones repartidas uniformemente, a compresión de un lado del alma y a tracción en el otro lado. Por tanto, la clasificación de las alas es: c 150 = = 6,5 ≤ 10 ⋅ ε = 10 → Clase 1 tf 23 Estructuras de acero. Problemas. Secciones. tabla 5.4 3 Respecto al eje z-z, en flexión pura puede despreciarse la posibilidad de pandeo por la oposición del alma respecto al eje neutro. Así, puede considerarse que la sección pertenece a la Clase 1. 4. Sección sometida a flexión y compresión: HEA 500 S-235 La sección está sometida a flexión respecto al eje y-y y a una fuerza de compresión axial de 400 kN. Clasificación del ala c 150 = = 6,5 < 10 ⋅ ε = 10 → Clase 1 tf 23 tabla 5.4 Clasificación del alma c = d = 390 mm c 390 = = 32,5 tw 12 Este valor es más bajo que el límite de c/tw en el caso de compresión uniforme del alma (33·ε=33), que es el caso de reparto de tensiones en el alma más 2. Así, el alma puede clasificarse de desfavorable 33 ⋅ ε, 72 ⋅ ε, 396 ⋅ ε ( ) ⋅ α − 13 1 Clase 1, independientemente del reparto de tensiones a que está sometida. Por tanto, la sección puede considerarse de Clase 1. 5. Sección sometida a flexión y compresión: IPE 600 S-355 La sección está sometida a flexión respecto al eje y-y y a una fuerza de compresión axial de 1200 kN. Clasificación del ala c = 110 mm c 110 = = 5,8 < 10 ⋅ ε = 8,1 → Clase 1 tf 19 2 tabla 5.4 Tabla 5.3. Casos de compresión, flexión simple y flexocompresión. Estructuras de acero. Problemas. Secciones. 4 Clasificación del alma c = d = 514 mm c 514 = = 42,8 tw 12 Este valor es más bajo que cualquier límite del alma en flexión pura (72·ε=58,3), pero supera el valor limite de la clase 3 en compresión pura (42·ε=34,0). La cuestión que se plantea es: ¿cómo es el reparto de tensiones, elástico o plástico? Supongamos en primer lugar una redistribución de tensiones totalmente plástica. Si se designa por cN la parte del alma que absorbe la compresión (profundidad de la fibra neutra), se tiene: NEd = c N ⋅ t w ⋅ f y → c N = α⋅c = α= NEd t w ⋅ fy c + cN 2 1 1 c ⋅ (c + c N ) = ⋅ 1 + N 2⋅c 2 c Introduciendo el valor de cN en esta expresión, se tiene: α= NEd 1 1200 ⋅ 10 3 1 = 0,774 ⋅ 1+ = ⋅ 1 + 2 t w ⋅ f y ⋅ c 2 12 ⋅ 355 ⋅ 514 Por tanto, ahora se pueden obtener los valores límites que definen la Clase de sección (tabla 5.3). Límite Clase 1: c 396 ⋅ ε ≤ = 33,8 t w 13 ⋅ α − 1 Límite Clase 2: c 456 ⋅ ε ≤ = 40,9 t w 13 ⋅ α − 1 Como c/tw supera este valor, habrá una distribución elástica de tensiones, y no plástica como se había supuesto. Estructuras de acero. Problemas. Secciones. 5 El reparto de tensiones en el alma que se considera es tal que la fibra extrema en compresión está en fluencia. La tensión debida al momento flector es igual a σb. Las tensiones en las fibras extremas del alma vienen dadas por las siguientes expresiones. fy = σb + Nw c ⋅ tw Nw c ⋅ tw ψ ⋅ f y = −σ b + siendo Nw la parte de esfuerzo axial que incide en el alma, igual a Nw = Aw ⋅ NEd , y A Aw el área del alma, de valor A w = c ⋅ t w y A el área de la sección. Por tanto, las expresiones anteriores pueden escribirse de la forma: fy = σb + NEd A ψ ⋅ f y = −σ b + NEd A Sumando estas expresiones se tiene: NEd A N f y ⋅ (1 + ψ ) = 2 ⋅ Ed A fy + ψ ⋅ fy = 2 ⋅ Estructuras de acero. Problemas. Secciones. 6 ψ= 1 2 ⋅ NEd ⋅ − 1 fy A ψ= 1 2 ⋅ 1200 ⋅ 10 3 ⋅ − 1 = 0,431 3 355 15,6 ⋅ 10 El valor límite de la Clase 3 es (tabla 5.3): 42 ⋅ ε 42 ⋅ 0,81 = = 41,9 0.67 + 0.33 ⋅ ψ 0,67 + 0,33 ⋅ 0,431 Como c = 48,8 > 41,9 → Clase 4 tw Por tanto, la sección pertenece a la Clase 4. 6. Sección soldada sometida a flexión y compresión Flexión alrededor del eje z-z y una fuerza de compresión axial de 300 kN. Datos fy = 355 N/mm2 ε = 235 fy = 0,81 h = 300 mm b = 300 mm tf = 12 mm tw = 8 mm a = 6 mm Estructuras de acero. Problemas. Secciones. 7 Clasificación de las alas Suponiendo un reparto plástico de tensiones, las alas están sometidas a una tensión uniforme igual a fy en la zona de compresión. c = 150 − 8 − 6 ⋅ 2 = 137,5 mm 2 c 137,5 = = 11,46 tf 12 c Este valor supera el valor límite de la Clase 3 ≤ 14 ⋅ ε = 11,34 , lo que tf significa que debe considerarse un reparto elástico. Se asume que en la fibra extrema en compresión está en fluencia. NEd σ2 300 ⋅ 10 3 ψ= = = = 0,09 σ1 A ⋅ f y 9408 ⋅ 355 k σ = 0,57 − 0,21 ⋅ ψ + 0,07 ⋅ ψ 2 = 0,55 tabla 5.4 c ≤ 21 ⋅ ε ⋅ k σ tf tabla 5.4 c = 11,46 < 21 ⋅ 0,81 ⋅ 0,55 = 12,6 → Clase 3 tf Clasificación del alma El alma está en compresión c = 300 − 2 ⋅ 12 − 2 ⋅ 6 2 = 259 mm c 259 = = 32,4 tw 8 Estructuras de acero. Problemas. Secciones. 8 c = 32,4 > 38 ⋅ ε = 30,78 → No es de Clase 2 tw tabla 5.3 c = 32,4 ≤ 42 ⋅ ε = 34,02 → Clase 3 tw Por tanto, la sección es de Clase 3 Estructuras de acero. Problemas. Secciones. 9