PAS - Sites
Anuncio
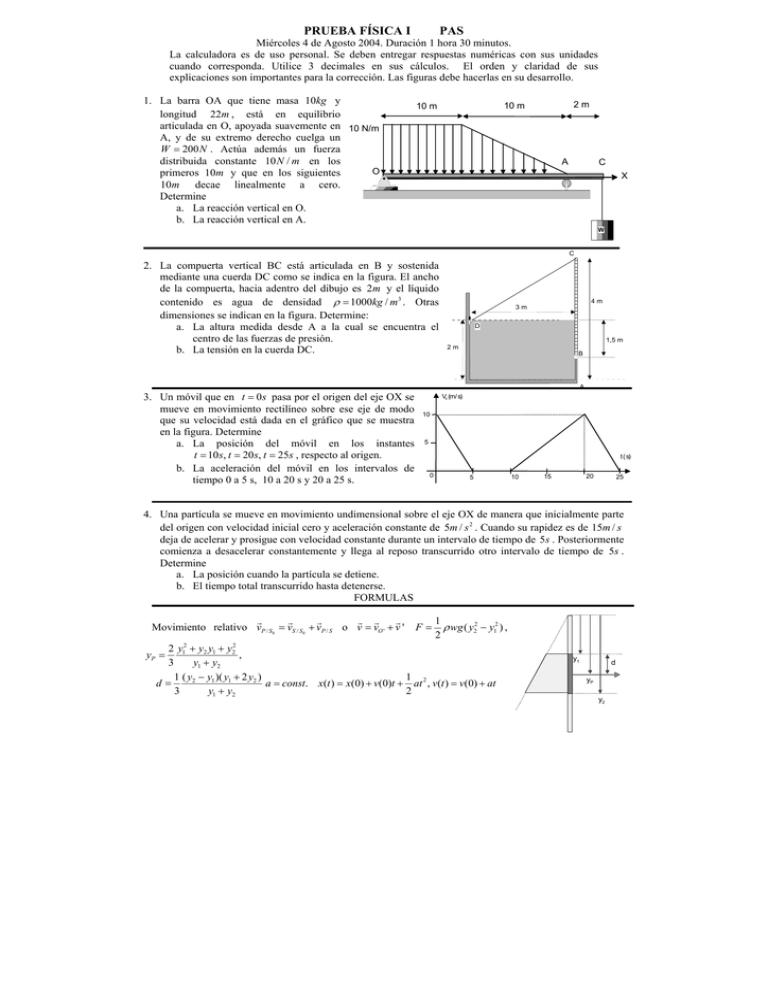
PRUEBA FÍSICA I PAS Miércoles 4 de Agosto 2004. Duración 1 hora 30 minutos. La calculadora es de uso personal. Se deben entregar respuestas numéricas con sus unidades cuando corresponda. Utilice 3 decimales en sus cálculos. El orden y claridad de sus explicaciones son importantes para la corrección. Las figuras debe hacerlas en su desarrollo. 1. La barra OA que tiene masa 10kg y longitud 22m , está en equilibrio articulada en O, apoyada suavemente en 10 N/m A, y de su extremo derecho cuelga un W = 200 N . Actúa además un fuerza distribuida constante 10 N / m en los O primeros 10m y que en los siguientes 10m decae linealmente a cero. Determine a. La reacción vertical en O. b. La reacción vertical en A. 2m 10 m 10 m A C X W C 2. La compuerta vertical BC está articulada en B y sostenida mediante una cuerda DC como se indica en la figura. El ancho de la compuerta, hacia adentro del dibujo es 2m y el líquido contenido es agua de densidad ρ = 1000kg / m3 . Otras dimensiones se indican en la figura. Determine: a. La altura medida desde A a la cual se encuentra el centro de las fuerzas de presión. b. La tensión en la cuerda DC. 3. Un móvil que en t = 0 s pasa por el origen del eje OX se mueve en movimiento rectilíneo sobre ese eje de modo que su velocidad está dada en el gráfico que se muestra en la figura. Determine a. La posición del móvil en los instantes t = 10s, t = 20s, t = 25s , respecto al origen. b. La aceleración del móvil en los intervalos de tiempo 0 a 5 s, 10 a 20 s y 20 a 25 s. 4m 3m D 1,5 m 2m B A Vx (m/ s) 10 5 t ( s) 0 5 10 20 15 25 4. Una partícula se mueve en movimiento undimensional sobre el eje OX de manera que inicialmente parte del origen con velocidad inicial cero y aceleración constante de 5m / s 2 . Cuando su rapidez es de 15m / s deja de acelerar y prosigue con velocidad constante durante un intervalo de tiempo de 5s . Posteriormente comienza a desacelerar constantemente y llega al reposo transcurrido otro intervalo de tiempo de 5s . Determine a. La posición cuando la partícula se detiene. b. El tiempo total transcurrido hasta detenerse. FORMULAS r r r r r r Movimiento relativo vP / S0 = vS / S0 + vP / S o v = vO ' + v ' F= 1 ρ wg ( y22 − y12 ) , 2 2 y12 + y2 y1 + y22 yP = , 3 y1 + y2 1 ( y2 − y1 )( y1 + 2 y2 ) 1 d= a = const. x(t ) = x(0) + v(0)t + at 2 , v(t ) = v(0) + at y1 + y2 2 3 y1 d yP y2 PAUTA PAS Física I Plan anual Hay un punto (1p), base en cada problema y se le suman los indicados. (Si hay algún error se arreglará). 1.- LA LONGITUD DE LA BARRA ES 22 m. Si lo hacen con 12 m por favor corriga Ud. La fuerza distribuida se reemplaza por una fuerza igual al área de la distribución 2m 10 m 10 m 10 N/m A O C X W 1 F = A1 + A2 = 10 × 10 + 10 × 10 = 150 N 2 el punto de aplicación puede calcularse 5 × 100 + (10 + x1 A1 + x2 A2 x= = A1 + A2 100 + 50 10 )50 3 = 70 = 7. 778 m 9 (1p) (1p) (o de la manera que lo expresen, si está bien) El diagrama de fuerzas queda como sigue: ahora, la tensión T es evidentemente el peso que cuelga de la cuerda es decir T = 200 N. La barra tiene un peso 100 N luego X ) Fy = VO + VA − 150 − 100 − 200 = 0 X (2p) − 100 × 11 − 200 × 22) k̂ = 0 ΓO = (20VA − 150 × 70 9 o 20VA − 20 000 =0 3 1 de aquí se obtiene 1000 = 333. 333 N 3 350 = 116. 667 N = 3 VA = VO 2 (b) 1 p) (a) 1p) 2.- De la figura tomando el eje y hacia abajo con origen al nivel del agua, se calcula con y1 = 0, y2 = 1.5 1 1 ρwg(y22 − y12 ) = 1000 × 2 × 10(1.52 ) = 22500.0 N (1p) 2 2 2 y12 + y1 y2 + y22 2 = = (1.5) = 1 m (1p) 3 y1 + y2 3 F = yP El ángulo α que forma la cuerda con a horizontal en D estará dado por = 1.0 4−2 tan α = ⇒ α = 33. 703o (1p) 3 2 (1.5) 3 C 4m 3m D 1,5 m 2m B A a) Medido desde A el centro de presión se encuentra a una altura h = 2 − 1 = 1m (1 p) b) Si llamamos T la tensión, haciendo torque respecto al punto B se obtiene X ΓB = (T × 3.5 × cos α − F (1.5 − 1))k̂ = 0 (1 p) de donde T = 3863. 09 N (1p) 3.- Respecto a la figura como inicialmente x(0) = 0, las posiciones futuras se obtienen agregando área bajo la curva.Así resulta 3 Vx (m/ s) 10 5 t ( s) 0 15 10 5 20 25 Figure 1: a) 1 10 × 5 = 25 m 2 1 1 x(20) = 10 × 5 + 10 × 10 = 75 m 2 2 1 1 1 x(25) = 10 × 5 + 10 × 10 + 10 × 5 = 100 m 2 2 2 b) las aceleraciones son x(10) = 0 − 10 = −2 m s−2 5 10 = 1 m s−2 a = 20 − 10 0 − 10 = −2 m s−2 a = 5 a = (1p) (1p) (1p) (1p) (1p) (1p) 4.- PUEDE HACERSE EN FORMA GRÁFICA, en ese caso Ud. evalúa. Para el primer tramo 1 2 5 2 at = t x(t) = 2 2 v(t) = at = 5t este tramo termina cuando v = 15 = 5t ⇒ t = 3 s 5 2 45 x = 3 = = 22. 5 m 2 2 4 (1p) luego avanza con rapidez constante durante 5 s recorriendo 5 × 15 = 75 m (1p) Ahora su velocidad llega a cero en otro intevalo de tiempo de 5 s, luego la aceleración en este tramo será a= 0 − 15 = −3 m s−2 5 (1p) y entonces recorrera otro espacio dado por 1 1 75 vt + at2 = 15 × 5 − × 3 × 52 = = 37. 5 m 2 2 2 (1p) La posición final será x = 22.5 + 75 + 37. 5 = 135.0 m (1p) t = 3 + 5 + 5 = 13 s (1p) y el tiempo total 5






