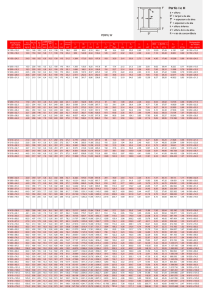
tf tf d bf tw - U
Anuncio
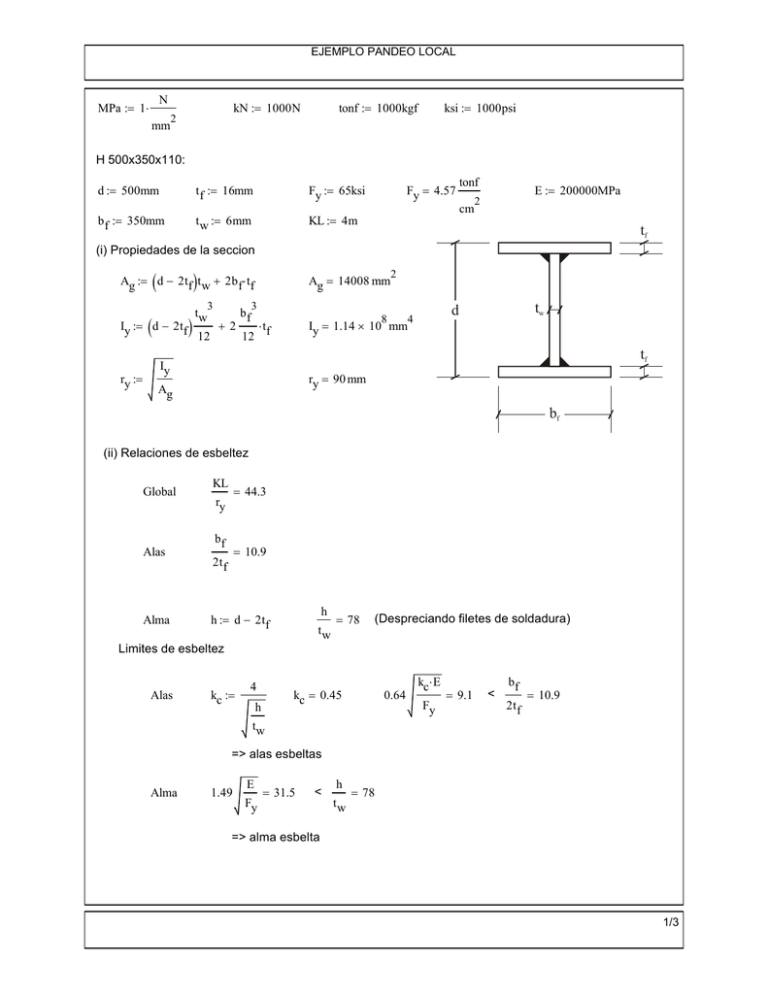
EJEMPLO PANDEO LOCAL N MPa := 1⋅ mm kN := 1000N 2 tonf := 1000kgf ksi := 1000psi H 500x350x110: d := 500mm t f := 16mm Fy := 65ksi b f := 350mm t w := 6mm KL := 4m Fy = 4.57 tonf cm E := 200000MPa 2 tf (i) Propiedades de la seccion ( ) Ag := d − 2tf t w + 2b f ⋅ tf 3 ( ) tw bf Ag = 14008 mm 3 8 Iy := d − 2tf +2 ⋅t 12 12 f ry := 2 tw d 4 Iy = 1.14 × 10 mm tf Iy ry = 90 mm Ag bf (ii) Relaciones de esbeltez Global Alas Alma KL = 44.3 ry bf = 10.9 2t f h h := d − 2tf tw = 78 (Despreciando filetes de soldadura) Limites de esbeltez Alas kc := 4 kc = 0.45 h 0.64 kc⋅ E Fy = 9.1 < bf 2t f = 10.9 tw => alas esbeltas Alma 1.49 E Fy = 31.5 < h tw = 78 => alma esbelta 1/3 EJEMPLO PANDEO LOCAL (iii) Resistencia nominal - Elementos no atiesados (alas), Qs 0.64 kc⋅ E Fy = 9.1 bf < = 10.9 2t f < kc⋅ E 1.17 bf Fy 2t f kc⋅ E Q s := 1.415 − 0.65 Fy = 16.6 Q s = 0.91 - Elementos atiesados (alma), Qa Necesitamos determinar f = Fcr (Q=1) KL ry = 44.3 E < 4.71 Fy = 99.5 2 Fe := π E KL r y 2 Fe = 1007 MPa Fy Fe Fcr := 0.658 ⋅ Fy h tw = 78 Fcr = 372 MPa > 1.49 E f = 34.5 E 0.34 ⋅ 1− b e := 1.92⋅ t w⋅ f h t w Aeff := 2b f ⋅ t f + b e⋅ t w Q a := Aeff Ag f := Fcr E f b e = 240 mm Aeff = 12641 mm < h = 468 mm 2 Q a = 0.9 2/3 EJEMPLO PANDEO LOCAL - Tension critica: Q := Q s⋅ Q a KL ry = 44.3 Q = 0.83 < 4.71 E Q ⋅ Fy = 109.5 Q⋅ Fy Fe Fcr := Q ⋅ 0.658 ⋅ Fy Fcr = 317 MPa - Resistencia nominal Pn := Fcr⋅ Ag Pn = 4444 kN Pn = 453 tonf 3/3