K-Nearest Neighbors - Gráficas, estadística y minería de datos con

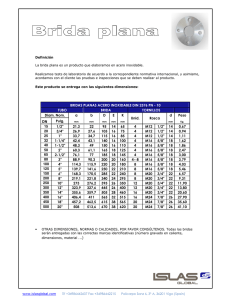
K-Nearest Neighbors
Gráficas, estadı́stica y minerı́a de datos con python
Miguel Cárdenas Montes
Centro de Investigaciones Energéticas Medioambientales y Tecnológicas,
Madrid, Spain
miguel.cardenas@ciemat.es
2-6 de Noviembre de 2015
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
1 / 29
Tabla de Contenidos
1
Objetivos
2
Introducción
3
Ejemplos Python
4
Ejemplos R
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
2 / 29
Objetivos
Conocer las diferencias entre los métodos de aprendizaje supervisado
impacientes y los métodos de aprendizaje supervisado perezosos.
Conocer algunas medidas de distancia.
Conocer métodos de aprendizaje con pesos.
Aspectos Técnicos
scikit-learn API
K-Nearest Neighbors
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
3 / 29
Introducción
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
4 / 29
KNN I
K-Nearest Neighbors (KNN) es
un método de clasificación
supervisado (como SVM)
También puede utilizarse en
regresión.
KNN sirve para estimar una
función de densidad F (x/Cj )
que predice el valor x para la
clase Cj .
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
5 / 29
KNN II
La idea que fundamenta este algoritmo
es que el nuevo objeto se clasificará en
la clase más frecuente de sus K vecinos
más próximos.
Para resolver los casos de empate, se
puede añadir alguna regla heurı́stica
como puede ser el vecino más próximo.
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
6 / 29
KNN III
Si k=3, entonces la predicción
del cı́rculo verde será un
triángulo rojo.
Si k=5, entonces la predicción
del cı́rculo verde será un
cuadrado azul.
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
7 / 29
KNN IV
Para clasificación con KNN, la tupla (punto) desconocida es asignado
a la clase más común de los k vecinos más próximos.
Si k=1, entonces se asignará al vecino más próximo.
Si k es demasiado pequeño, entonces el resultado es muy sensible a
puntos ruidosos. Pero si k es demasiado grande, entonces la vecindad
del punto desconocido incluirá muchos puntos de otras clases lejanas.
Regla: k debe ser grande para disminuir la probabilidad de una mala
clasificación, pero pequeño en comparación con el número de puntos.
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
8 / 29
KNN V
KNN pierde precisión si se utilizan datos ruidosos o con atributos
irrelevantes.
Entonces es interesante sopesar los vecinos con la distancia que lo
separa
P de la tupla desconocida, weighted k-nearest neighbors,
y= ki=1 wi · yi , con wi = d(xtest1 ,x )2 .
i
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
9 / 29
KNN VI
Si se utiliza KNN con datos categóricos, el algoritmo devuelve la
categorı́a a la cual deberı́a pertener la tupla desconocida.
Si se utiliza KNN con datos continuos, el algoritmo devuelve la media
de los valores de los vecinos.
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
10 / 29
KNN VII
El uso de KNN en clasificación se fundamenta en el uso del voto
(mayorı́a) para decidir el valor más adecuado. El voto puede ser con
pesos o sin ellos.
Observación: si la clasificación es binaria, entonces es preferiblemente
elegir k impar para evitar empates.
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
11 / 29
KNN VIII
La elección de la métrica de la distancia es crı́tica para el rendimiento
del algoritmo.
v
u n
uX
(1)
D(X1 , X2 ) = t (x1i − x2i )2
i=1
Además hay que tener cuidado si tiene atributos con rangos muy
grandes (por ejemplo, ingresos) y otros con rangos pequeños (por
ejemplo atributo binario), ya que unos enmascarará a los otros. La
solución es normalizar adecuadamente todos los atributos.
v′ =
M. Cárdenas (CIEMAT)
v − vmin
vmax − vmin
KNN
(2)
2-6 de Noviembre de 2015
12 / 29
KNN IX
Ejemplos de distancia usadas en regresión:
wi
wi
wi
wi
= k1
≈ 1 − ||xi − x0 ||
= ||xi − x0 ||
≈ k − rank||xi − x0 ||
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
13 / 29
KNN X
Distancia Hamming: Si los atributos son categóricos, entonces la
propuesta de sitancia puede ser: distancia 1 si son diferentes y 0 si
son iguales.
Ejemplos de distancia Hamming:
La distancia de toned a roses es 3.
La distancia de 1011101 a 1001001 es 2.
La distancia de 2173896 a 2233796 es 3.
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
14 / 29
KNN XI
Otros algoritmos clasificatorios basan la clasificación de cada nuevo
caso en dos tareas.
Primero se induce el modelo clasificatorio (inducción), y
posteriormente, se deduce la clase del nuevo caso (deducción).
Sin embargo, en KNN ambas tareas están unidas (transducción).
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
15 / 29
Lazy Learners
KNN pertenece a un tipo de clasificadores denominado lazy learner,
”vago”.
SVM pertenece a otro tipo denominado eager learner, ”impaciente”.
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
16 / 29
Eager vs Lazy Learners
Eager Este tipo de clasificadores construyen un modelo
(clasificación) antes de recibir ningún dato perteneciente a
conjunto de predicción.
Por ejemplo, SVM construye el modelo con el conjunto de
datos de entrenamiento.
Lazy En este tipo de clasificadores la construcción del modelo se
retrasa hasta que se demanda la predicción.
Mientras tanto solo almacena los datos suministrados.
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
17 / 29
Complejidad Computacional de KNN
La complejidad computacional de KNN cuando es usado tal y como
se ha presentado es de O[D × N]; siendo N el número de tuplas y D
su dimensionalidad (número de caraterı́sticas).
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
18 / 29
KNN XII
Ejemplo de datos (150 objetos)
perteniences a tres clases.
4.5
Estudiaremos la variación del
número de clasificaciones
correctas. Consecutivamente se
quita un objeto del conjunto, se
entrena KNN con el conjunto
restante y se predice la clase del
elemento sustraı́do.
M. Cárdenas (CIEMAT)
KNN
4.0
3.5
3.0
2.5
2.0
4.5
5.0
5.5
6.0
6.5
7.0
7.5
2-6 de Noviembre de 2015
8.0
19 / 29
KNN XIII
122
120
Estudiaremos la
variación del número de
clasificaciones correctas.
Consecutivamente se
quita un objeto del
conjunto, se entrena
KNN con el conjunto
restante y se predice la
clase del elemento
sustraı́do.
118
116
114
112
110
108
106
0
5
10
K vecinos
15
20
25
4.5
4.0
3.5
3.0
2.5
2.0
4.5
M. Cárdenas (CIEMAT)
KNN
5.0
5.5
6.0
6.5
7.0
7.5
8.0
2-6 de Noviembre de 2015
20 / 29
KNN XIV
44
42
Estudiaremos la
variación del número de
clasificaciones
incorrectas.
Consecutivamente se
quita un objeto del
conjunto, se entrena
KNN con el conjunto
restante y se predice la
clase del elemento
sustraı́do.
40
38
36
34
32
30
28
0
5
10
K vecinos
15
20
25
4.5
4.0
3.5
3.0
2.5
2.0
4.5
M. Cárdenas (CIEMAT)
KNN
5.0
5.5
6.0
6.5
7.0
7.5
8.0
2-6 de Noviembre de 2015
21 / 29
Ejemplos Python
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
22 / 29
Ejemplo I
import numpy as np
import pylab as pl
import matplotlib
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
# first training set
2-Class classification (k = 3, weights = 'uniform')
X = np.r_[’1,2,0’, \
[12.9, 13.3, 15.2, 14.2, 11.8, 21.4, 12., 31., 31., 30.5, 31., 32., 31., 33.2, 34.4, 32.9], \
[12.9, 15.1, 13.1, 15.0, 10.7, 22.6, 31., 11., 30., 31.5, 3025., 24., 32., 22.1, 31.3, 21.3] ]
Y = [0, 0, 0, 0, 0, 0, 0, 0, \
1, 1, 1, 1, 1, 1, 1, 1]
25
h = 1 # step size in the mesh
n_neighbors = 5
20
15
# Create color maps
cmap_light = ListedColormap([’#FFAAAA’, ’#AAFFAA’, ’#AAAAFF’])
cmap_bold = ListedColormap([’#FF’, ’#FF’, ’#FF’])
10
10
15
20
25
30
35
for weights in [’uniform’]:
...
...
...
pl.savefig(’knn-basic_1A.eps’)
pl.show()
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
23 / 29
Ejemplo II
for weights in [’uniform’]:
# we create an instance of Neighbours Classifier and fit the data.
clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
clf.fit(X, Y)
# Plot the decision boundary. For that, we will asign a color to each
# point in the mesh [x_min, m_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
2-Class classification (k = 3, weights = 'uniform')
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
30
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min,
y_max, h))
#print xx,yy
25
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
#print Z
pl.figure()
pl.pcolormesh(xx, yy, Z)
20
15
10
10
15
20
25
30
35
# Plot also the training points
pl.scatter(X[:, 0], X[:, 1], c=Y, cmap=cmap_light)
pl.title("3-Class classification (k = %i, weights = ’%s’)" % (n_neighbors, weights))
pl.axis(’tight’)
pl.savefig(’knn-basic_1A.eps’)
pl.show()
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
24 / 29
Ejemplo III
El factor K (número de vecinos) afecta a la apariencia del mapa, pero
el factor paso del muestreo también puede afectar.
Los usos de KNN son similares a SVM: además del uso para
clasificación, se puede usar para regresión.
2-Class classification (k = 3, weights = 'uniform')
2-Class classification (k = 5, weights = 'uniform')
2-Class classification (k = 9, weights = 'uniform')
30
30
30
25
25
25
20
20
20
15
15
15
10
10
10
10
15
20
25
M. Cárdenas (CIEMAT)
30
35
10
15
20
KNN
25
30
35
10
15
20
25
30
2-6 de Noviembre de 2015
35
25 / 29
Ejemplo IV
Añadir puntos de una nueva clase supone la reorganización
automática del mapa predictivo.
No hay lı́mite en el número de clases siempre y cuando tengan un
representación significativa.
2-Class classification (k = 5, weights = 'uniform')
30
25
20
15
10
10
M. Cárdenas (CIEMAT)
15
20
25
KNN
30
35
2-6 de Noviembre de 2015
26 / 29
Ejemplos R
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
27 / 29
Ejemplo I
# Clase A
A1=c(0,0)
A2=c(1,1)
A3=c(2,2)
# Clase B
B1=c(6,6)
B2=c(5.5,7)
B3=c(6.5,5)
# Matriz de datos de entrenamiento
train=rbind(A1,A2,A3, B1,B2,B3)
# Vector de etiquetas
cl=factor(c(rep("A",3),rep("B",3)))
# Objeto test
test=c(4, 4)
Salida (indica que el punto de test
pertenece a la clase B):
A B
0 1
# Cargar libreria
library(class)
# Entrenamiento y prediccion
summary(knn(train, test, cl, l = 0, k = 1))
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
28 / 29
Gracias
Gracias
¿Preguntas?
¿Más preguntas?
M. Cárdenas (CIEMAT)
KNN
2-6 de Noviembre de 2015
29 / 29