Ejercicio nº 6

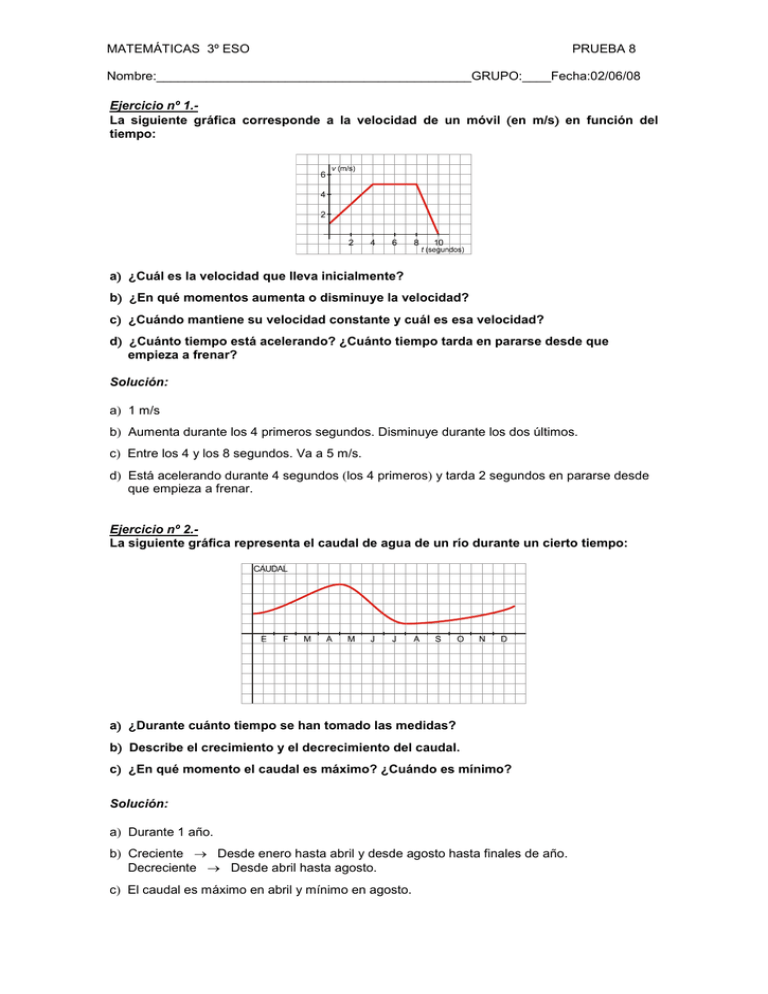
MATEMÁTICAS 3º ESO
PRUEBA 8
Nombre:____________________________________________GRUPO:____Fecha:02/06/08
Ejercicio nº 1.La siguiente gráfica corresponde a la velocidad de un móvil en m/s en función del
tiempo:
a ¿Cuál es la velocidad que lleva inicialmente?
b ¿En qué momentos aumenta o disminuye la velocidad?
c ¿Cuándo mantiene su velocidad constante y cuál es esa velocidad?
d ¿Cuánto tiempo está acelerando? ¿Cuánto tiempo tarda en pararse desde que
empieza a frenar?
Solución:
a 1 m/s
b Aumenta durante los 4 primeros segundos. Disminuye durante los dos últimos.
c Entre los 4 y los 8 segundos. Va a 5 m/s.
d Está acelerando durante 4 segundos los 4 primeros y tarda 2 segundos en pararse desde
que empieza a frenar.
Ejercicio nº 2.La siguiente gráfica representa el caudal de agua de un río durante un cierto tiempo:
a ¿Durante cuánto tiempo se han tomado las medidas?
b Describe el crecimiento y el decrecimiento del caudal.
c ¿En qué momento el caudal es máximo? ¿Cuándo es mínimo?
Solución:
a Durante 1 año.
b Creciente  Desde enero hasta abril y desde agosto hasta finales de año.
Decreciente  Desde abril hasta agosto.
c El caudal es máximo en abril y mínimo en agosto.
Ejercicio nº 3.Representa gráficamente las siguientes funciones:
a) y 
3
x 1
4
b 2x  3y  4
c y  3
Solución:
a Pasa por 0, 1 y 4, 2.
2x  4
3
Pasa por 2, 0 y 1, 2.
b) y 
c Paralela al eje X.
Ejercicio nº 4.Escribe la ecuación de cada una de las siguientes rectas:
a Pasa por los puntos P1, 9 y Q3, 7.
b
Solución:
a) m 
7   9 
3   1

7  9 16

4
3 1 4
Ecuación puntopendiente:
y  7  4  x  3

y  4x  5
b
Su pendiente es m 
1
.
2
Su ordenada en el origen es n  1.
Su ecuación será: y 
1
x 1
2
Ejercicio nº 5.Sabemos que 100 C equivalen a 80 Réaumur y que 20 C equivalen a 16 R.
a Obtén la ecuación de la recta que transforma los grados centígrados, x, en grados
en la escala Réaumur, y.
b Represéntala gráficamente.
c ¿A cuántos grados de la escala Réaumur equivalen 50 C?
Solución:
a Buscamos la ecuación de la recta que pasa por los puntos 100, 80 y 20, 16:
m
16  80 64

 0,8
20  100 80
Ecuación puntopendiente:
y  16  0,8  x  20

y  0,8x
b
c Si x  50 C, entonces: y  0,8 · 50  40 R
Ejercicio nº 6.Un ciclista sale a hacer ejercicio y pedalea a 15 km/h. Media hora más tarde sale en su
busca un motorista a 60 km/h.
a) Representa las funciones que dan el espacio recorrido por cada uno en función del
tiempo y escribe sus expresiones analíticas.
b) ¿Cuánto tardará el motorista en alcanzar al ciclista?
Solución:
a) Espacio recorrido por el ciclista (y )

  y  15 x
en función del tiempo, en horas, transcurrido (x ). 
Espacio recorrido por el motorista (y )

1

  y  60  x  
en función del tiempo, en horas, transcurrido (x ). 
2

Representamos ambas funciones:
1

y  15x
y  60  x    y  60x  30
2


x 0 1
y 0 15
x 12 1
y 0 30
b) El encuentro se producirá cuando ambos hayan recorrido la misma distancia, en este caso,
a los 40 minutos de salir el ciclista.