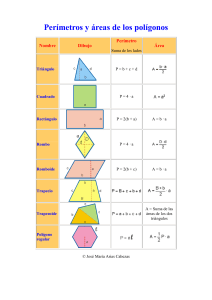
A(r,t) = Ao(r,t). e Φ= k.r - ωt - θ φ = (k2 - k1).r (división
Anuncio

PRINCIPIO DE LA INTERFEROMETRIA A DOS HACES Representación compleja de una componente del campo quasimonocromático (onda electromagnética) A(r,t) = Ao(r,t). ej( k.r - ω t - θ ) con Ao(r,t) amplitud de variación “lenta” respecto al término oscilante ej(ω t -kr - θ ). k ≡ 2π π /λ λ representa el módulo del vector de onda y λ la longitud de onda Función de fase óptica o simplemente fase de la onda Φ = k.r - ω t - θ Introducción de una diferencia de fase φ , retardo óptico τ o diferencia de camino óptico ∆ L entre dos ondas φ = (k2 - k1).r (división del frente de onda) φ = 2π π ∆ L/λ λ =ω ωτ ó (división de amplitud) ∆ L =ncττ, con n = índice de refracción del medio Rafael A. Escalona Z. Página 1 04/22/03 Superposición espacial y temporal de dos ondas ⇒ ⇒ INTERFERENCIA ! Atotal(r,t) = Ao1(r,t). ej( k1.r - ω 1t - θ 1) + Ao2(r,t). ej( k2.r - ω 2t - θ 2+ φ ) Detección cuadrática (energía) del campo resultante Intensidad luminosa I: < Atotal(r,t). Atotal*(r,t) >t donde (...)* es el complejo conjugado y < ... >t denota un promedio temporal Expresión general de la interferencia a dos haces I ∝ I1 + I2 + 2√ I1I2.Re[ γ 12(φ ) ] con I1 = <Ao1(r,t).Ao1(r,t)*>t y I2 = < Ao2(r,t).Ao2(r,t)*>t “Re” indica la parte real Rafael A. Escalona Z. Página 2 04/22/03 γ 12(r,θ θ 1,θ θ 2,φ φ ) ≡ ejφ [ < Ao1(r,t)ejθ 1 (Ao2(r,t)ejθ 2)*>t /√ √ I1I2 ] es la función de coherencia compleja normalizada de orden dos del campo total. Una expresión más simplificada es I ∝ I1 + I2 + 2√ √ I1I2 γ (0)cos(φ φ - α) en donde γ (0) es el grado de coherencia de orden 2 del campo y el ángulo α es el argumento de <A ejθ 1 (A ejθ 2)*> o1 o2 Referencias básicas mínimas acerca del fenómeno de interferencia: -) Principles of Optics, M. Born and E. Wolf, 5ta. edición, Pergamon Press (1975). -) Vibrations lumineuses et optique cohérente, Maurice Françon, ed. Dunod (1970). -) Progress in Optics, Vol. XXVI, K. Creath, pp 349-393, (1988). -) “Review of Phase-Measuring Interferometry”, H. P. Stahl, Proc. SPIE Vol. 1332, Pt. 2, pp 704-719 (1990). Rafael A. Escalona Z. Página 3 04/22/03