Tema 8 Interacción nuclear - Colegio Sagrado Corazón de Granada

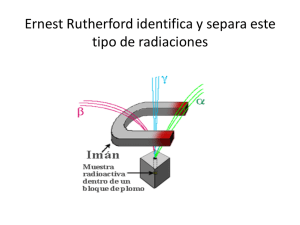
Tema 8
Interacción nuclear
8.1. Composición del núcleo atómico; nucleones.
8.2. Interacción nuclear fuerte.
8.3. Estabilidad nuclear: energía de enlace.
8.4. Radioactividad: emisiones radiactivas. Magnitudes y leyes.
8.5. Fusión y fisión nucleares.
8.6. Aplicaciones de la radiactividad y las reacciones nucleares.
8.7. Revisión de las interacciones fundamentales de la naturaleza.
8.1. Composición del núcleo atómico: nucleones.
8.1.1. Revisión de los modelos atómicos: núcleo y electrones.
La primera noción de átomo se debe a Demócrito en torno al año 400 a.C que supuso
que la materia estaba formada por pequeñas partículas indivisibles e inapreciables para los
sentidos. La palabra átomo significa indivisible en griego. Los descubrimientos de la
radiactividad (Becquerel) y del electrón (Thomson) a finales del siglo XIX pusieron de
manifiesto que realmente los átomos no eran indivisibles ya que se podían descomponer en
partículas menores.
En 1907 Thomson propuso un modelo en el que el átomo estaba formado por una
masa densa cargada positivamente y en la que los electrones estaban embebidos de manera
similar a como las pasas están distribuidas en el interior de un pastel.
Los
experimentos
partículas
α
realizados
por
por
láminas
Geiger
y
de
dispersión
metálicas
Marsden
de
delgadas
llevaron
a
Rutherford a proponer otro modelo de átomo en el
que toda la carga positiva y prácticamente toda la
masa se encontraban en un núcleo de dimensiones
muy reducidas (≈10−14 m), y los electrones en la
corteza del átomo (≈10−10 m). El experimento
Figura 8.1. Dispersión de partículas α por
una lámina delgada
Tema 8: Interacción nuclear
Física 2º Bachillerato
consistió en lanzar partículas α (núcleos de He) contra una lámina delgada de oro. La mayoría
de ellas seguían su trayectoria, unas pocas sufrían desviaciones de ángulo variable y algunas
experimentaban auténticos rebotes, saliendo despedidas hacia atrás. Se postuló entonces que
los átomos estaban formados por dos tipos de partículas subatómicas, los electrones con carga
negativa, situados en la corteza y con capacidad para abandonar el átomo dejándolo
convertido en un ión, y los protones de carga positiva fijos en el interior del núcleo y de una
masa entre mil y dos mil veces mayor que la del electrón. La carga de un protón es la misma
que la de un electrón por lo que, en un átomo neutro, deben coincidir el número de electrones y
protones.
Asumido este modelo surgió un problema con la masa de los núcleos atómicos.
Suponiendo que la masa de un átomo de hidrógeno era la de un protón, las masas del resto de
los átomos eran superiores a la suma de los protones que se suponía debían tener. Al principio
se supuso que en los núcleos habría más protones que deberían estar neutralizados por
electrones adicionales que también estarían situados en el núcleo, pero en 1934 Chadwick
detectó la presencia de una nueva partícula en el átomo. No tenía carga y su masa era
ligeramente mayor que la del protón, se la llamó neutrón.
Según el modelo de Rutherford los electrones estarían dispuestos en órbitas circulares
alrededor del núcleo. Más adelante Bohr estableció la cuantización de la energía de los
electrones y determinó que solamente eran posibles unas órbitas determinadas. Más adelante,
y aplicando la hipótesis de De Broglie y el principio de incertidumbre de Heisemberg los
electrones están representados por funciones de onda que representan la probabilidad que un
electrón se encuentre en una posición y se cambia el concepto determinista de órbita al
probabilístico de orbital.
8.1.2. Partículas nucleares; protón y neutrón.
La conclusión final es que los átomos están formados por un núcleo extremadamente
pequeño que contiene a los nucleones (protones y neutrones), y una corteza formada por
diferentes capas de orbitales donde se encuentran los electrones. Dado que los electrones son
unas 1840 veces más ligeros que los protones y neutrones, la masa de una átomo se puede
decir que es la masa de su núcleo. Como el núcleo es aproximadamente diez mil veces más
pequeño que el átomo, la densidad nuclear es muy elevada.
La densidad del núcleo puede ser considerada constante, por lo que el volumen
nuclear V es proporcional al número de nucleones A llamado número másico. Se puede
establecer una relación entre el radio nuclear y el número másico:
Tema 8-2
Colegio Sagrado Corazón
V =k⋅A
4
π ⋅r3 = k ⋅ A
3
r = k'⋅A 1/3
siendo k’ = 1.2 ·10-15m, aproximadamente constante para todos los núcleos. Este valor tan
pequeño motivó la conveniencia de definir una nueva unidad de longitud para las medidas de
núcleos, el fermi; 1fermi = 10−15m.
8.1.3. Número másico y número atómico. Isótopos. Representación.
Existen dos números que indican la composición del núcleo:
•
número másico (A); representa el número total de nucleones, es decir protones
más neutrones;
•
número atómico (Z); es el número de protones que coincide con el de electrones
en los átomos neutros.
La representación en el sistema internacional de un átomo cualquiera es la siguiente:
A +...+ / −...−
ZX
En función de Z y A se definen:
•
isótopos son los átomos que teniendo igual número atómico tienen diferente
número másico. Estos átomos tienen prácticamente las mismas propiedades
químicas ya que éstas dependen de los electrones de la corteza;
•
isótonos son los que tienen el mismo número de neutrones.
Para medir la masa de un nucleón, se toma como referencia la doceava parte del
isótopo 12 del carbono. A esta cantidad se la llama unidad de masa atómica (uma). Con esta
convención se establecen las masas de las partículas subatómicas tal como se muestra en la
tabla 1.
Partícula
nucleones
Carga (C)
Masa (uma)
electrón
−1.6 · 10-19
0,000549
corteza
protón
1.6 · 10-19
1,007277
núcleo
1,008665
núcleo
neutrón
0
Localización
Tabla 8.1. Características y localización de las partículas subatómicas.
8.2. Interacción nuclear fuerte
Como se ha visto, el núcleo atómico contiene a los protones y neutrones del átomo.
Los protones tienden a separarse debido a las fuerzas eléctricas de repulsión entre ellos sin
Tema 8-3
Tema 8: Interacción nuclear
Física 2º Bachillerato
embargo, la mayoría de los núcleos que se encuentran en la naturaleza son muy estables, es
decir, no se descomponen como consecuencia de estas intensas fuerzas repulsivas. Deben
existir otro tipo de fuerzas que mantienen unidos a los protones en el núcleo bastante más
intensas que las fuerzas eléctricas. Además, esta interacción se observa sólo cuando los
protones están muy próximos entre sí, por lo que deben ser de muy corto alcance. A esta
nueva interacción, que no es de origen gravitatorio ni eléctrico, se la denomina interacción
nuclear fuerte.
En las interacciones entre átomos y moléculas las fuerzas predominantes son las de
origen eléctrico (lo que incluye a las de tipo magnético) sin embargo, a nivel nuclear, las
fuerzas predominantes son las debidas a la interacción nuclear fuerte. Las características
importantes de esta nueva interacción son las siguientes.
1. Gran intensidad; unas 100 veces más intensas que las electrostáticas y 1040
veces más que las gravitatorias. Debido a esta diferencia, el orden de magnitud de
la energía es muy diferente cuando se estudian procesos atómicos y moleculares a
cuando se estudian procesos nucleares. Las energías involucradas en procesos
nucleares son del orden de los MeV, mientras que en procesos de la corteza del
átomo son de eV.
2. Corto alcance; menos de 10-13m. Por eso sólo se tienen en cuenta en el interior de
los núcleos y no en otros procesos.
3. Carácter atractivo a corta distancia y repulsivo a muy corta distancia; a corta
distancia es una interacción atractiva, y por eso los protones permanecen unidos
en el núcleo; pero a muy corta distancia debe ser repulsiva ya que, de no ser así,
los nucleones colapsarían en el núcleo.
4. Saturada; cada nucleón interacciona con un número determinado de nucleones,
por encima del cual no ejerce influencia sobre otros.
5.
Independiente de la carga; la interacción nuclear fuerte ocurre entre protones,
entre neutrones y entre protones y neutrones indistintamente.
F
F
r
Int. nuclear fuerte
Int. electrostática
(a)
r
Efecto total
(b)
Figura 8.2. (a) Representación de las interacciones electrostática y nuclear fuerte entre
dos protones. (b) Fuerza resultante de las dos anteriores. Las fuerzas positivas
representan repulsión y las negativas atracción.
Tema 8-4
Colegio Sagrado Corazón
Como se puede apreciar en la figura 8.2. para largas distancias (>10–13m) los protones
experimentan una fuerza de repulsión propia del efecto electrostático. A medida que se
acercan la repulsión aumenta hasta el punto que empiezan a actuar las fuerzas nucleares, que
predominan sobre las eléctricas al ser más intensas. A partir de un punto determinado los
protones dejan de sentir una fuerza total de repulsión y comienzan a atraerse hasta que están
muy próximos entre sí, momento en el cual la interacción fuerte los mantiene a distancia. La
gráfica de la figura 8.2 corresponde a la interacción protón-protón. En los casos protón-neutrón
y neutrón-neutrón solamente se tienen en cuenta la componente de fuerzas de la interacción
fuerte.
8.3. Energía de enlace y estabilidad nuclear.
8.3.1 Defecto de masa y energía de enlace
En la formación de los núcleos atómicos se da un fenómeno conocido como defecto
de masa que consiste en que la masa de un núcleo es menor que la suma de las masas
individuales de los protones y neutrones que lo forman.
El defecto de masa se calcula restando la masa por separado de los protones y neutrones
menos la masa del núcleo:
(
)
Δm = Z ⋅ m p + (A − Z ) ⋅ m n − Mnúcleo
Esta masa que falta equivale a la energía de enlace que es la que se liberaría si el
núcleo se formase a partir de sus nucleones:
E e = Δm ⋅ c 2
La expresión anterior establece una equivalencia entre dos magnitudes que hasta
ahora han sido independientes; la masa y la energía. La masa tiene una equivalencia en
energía y viceversa. El elevado valor de c implica que pequeñas cantidades de masa se
pueden convertir en grandes cantidades de energía. Por ejemplo, 1g de masa que se
desintegre completamente genera 9·1013J (90 billones de julios) más de la energía que genera
una central nuclear en un año de funcionamiento ininterrumpido.
La energía de enlace también se puede interpretar como la energía que es necesaria
para deshacer el núcleo en sus nucleones.
Tema 8-5
Tema 8: Interacción nuclear
Física 2º Bachillerato
La energía de enlace por nucleón se define como la energía de enlace entre el
número de nucleones del átomo.
E epn =
Δm ⋅ c 2
A
Esta energía representa de manera aproximada la energía necesaria para arrancar un
nucleón del núcleo.
8.3.2 Estabilidad nuclear
La estabilidad nuclear es la propiedad que tienen los núcleos de mantener constantes
sus números másico y atómico. Los núcleos poco estables tienden a fisionarse o a perder
nucleones con mucha facilidad. La energía de enlace por nucleón es un buen referente para
saber si un núcleo es estable. Como se puede apreciar en la gráfica de la figura 8.3, los
núcleos más estables (del orden de 9MeV/nucleón) corresponden a los números másicos en
torno a 60 (Fe, Co, Ni, Cu,...). Además se puede apreciar en la gráfica que determinados
núcleos son especialmente estables debido a su configuración nuclear (He, C, O y Al).
Figura 8.3. Energía media de enlace por nucleón en función del número másico
Si se representan en un plano Z-N (protones-neutrones) los diferentes núcleos
atómicos conocidos, se puede apreciar cómo la tendencia es que, a medida que aumenta el
número de protones, el número de neutrones aumenta más aún. La conclusión es que, en
principio, los neutrones dan estabilidad a los núcleos. Esta idea es razonable si se tienen en
Tema 8-6
Colegio Sagrado Corazón
cuenta algunas de las propiedades de la
interacción
fuerte;
muy
corto
alcance
y
saturación. En núcleos con gran número de
N
Línea de la
estabilidad
N=Z
nucleones las fuerzas nucleares fuertes que
mantienen unido al núcleo se saturan y, si el
tamaño del núcleo es grande, es posible que
las fuerzas eléctricas produzcan repulsiones
entre los protones más alejados por lo que los
núcleos masivos se vuelven inestables y es
necesaria
la
existencia
de
neutrones
adicionales que proporcionen estabilidad.
Z
Figura 8.4. Relación entre número de
protones y de neutrones de los núcleos
atómicos
Por otra parte, se observa cómo los núcleos más estables se encuentran formando la
llamada línea de la estabilidad, y los núcleos menos estables se encuentran alrededor de esa
línea. La tendencia de los núcleos inestables es aproximarse hacia la línea de la estabilidad
mediante emisiones radiactivas que modifican sus números másicos y atómicos. En la figura
8.4 se puede apreciar cómo la simple adición de neutrones no proporciona estabilidad, sino
que, además, debe existir una relación concreta entre protones y neutrones; no basta con
incluir más neutrones para proporcionar núcleos estables. Para que un núcleo sea estable
debe contener un número concreto de neutrones que generalmente es superior al de protones.
8.4. Radioactividad: emisiones radiactivas. Magnitudes y leyes.
8.4.1. Radiactividad natural y artificial
En 1895 Roentgen dio a conocer el descubrimiento de los rayos X y numerosos
científicos de la época comenzaron a investigar las propiedades y emisiones de este tipo de
radiación. En 1896 Antoine Henri Becquerel (Nobel en 1903) investigaba cómo sales de uranio
expuestas a la luz solar eran capaces de impresionar placas fotográficas cubiertas debido a la
emisión de rayos X. Becquerel interrumpió sus investigaciones durante varios días nublados y
guardó las placas fotográficas en un cajón junto a unas muestras de sales de uranio. Las
placas se impresionaron sin que el Sol incidiera sobre las sales de uranio por lo que Becquerel
dedujo que las sales debían de emitir radiación por sí mismas. Esta es la radiación natural,
debida a la transformación espontánea de un núcleo a otro en materiales que se encuentran en
la naturaleza. El matrimonio Marie y Pierre Curie (premios Nobel en 1903 y 1911) descubrieron
otros materiales que también emitían radiaciones Ra, Po,... en la actualidad se conocen unos
70 materiales naturales que emiten radiaciones.
Otras veces el hombre produce de forma artificial núcleos que no se encuentran en la
naturaleza. Si el núcleo producido no es estable se produce la radiación artificial. El primer
isótopo artificial fue producido por el matrimonio Joilot-Curie en 1934 (Nobel en 1935) al
Tema 8-7
Tema 8: Interacción nuclear
bombardear núcleos de
Física 2º Bachillerato
27
13 Al
con partículas α obteniendo
30
15
P, que es radiactivo y no se
encuentra en la naturaleza. Los términos radioactividad natural y artificial solamente hacen
referencia a si el material se encuentra en la naturaleza o es sintético, pero no existen
diferencias entre las radiaciones emitidas por ambos tipos de materiales.
8.4.2. Desintegración radiactiva; radiaciones alfa, beta y gamma
Se entiende por desintegración radiactiva la transformación de un núcleo en otro con
emisión de radiación o partículas. Presentan fenómenos radioactivos núcleos generalmente
pesados que se transforman en núcleos más ligeros.
Cuando tiene lugar una desintegración radiactiva se produce una emisión de partículas
o de energía que puede ser de tres tipos emisión alfa, beta o gamma.
1. Emisión alfa ( 24α + + ). Son núcleos de Helio; 2 protones y dos neutrones.
2. Emisión beta ( −10 β ). Son electrones a muy alta velocidad (hasta un 90% de la
velocidad de la luz).
3. Emisión gamma (γ). Radiación electromagnética de muy alta frecuencia, y por lo tanto
muy energética.
De cada tipo de radiación interesan conocer dos características, el poder de
ionización y el poder de penetración. El poder de ionización indica cuánto es capaz de
ionizar el medio por el que se propague la emisión y se mide en iones producidos por cm
recorrido. El poder de penetración es su capacidad para atravesar el medio por el que se
propague. Ambas magnitudes dependen de la masa, la carga y la velocidad de cada emisión.
La emisión alfa está formada por partículas pesadas y su velocidad de emisión es baja,
oscilando entre un 5% y un 7'5% de la velocidad de la luz. Su poder de ionización es el más
alto ya que tiende a captar electrones para convertirse en helio atómico y su poder de
penetración es muy bajo; unos 5cm en aire. La emisión beta son electrones a altas velocidades
cuya masa es menor que la de las partículas alfa, por lo tanto su poder de penetración es
mayor (1'5m de aire o 2mm de Pb). Su poder de ionización es menor. La emisión gamma es
radiación (fotones) y por tanto la más penetrante (semiabsorción en 0.5m de hormigón) y la
menos ionizante de las tres.
8.4.3. Leyes de la radiactividad; familias radiactivas
Cada una de las emisiones radiactivas corresponde a una transformación diferente del
núcleo atómico. En todas se cumplen varios principios fundamentales de conservación:
Tema 8-8
Colegio Sagrado Corazón
•
conservación del número total de nucleones;
•
conservación de la carga;
•
conservación de la masa-energía;
•
conservación de la cantidad de movimiento.
Además, y como consecuencia de algunos de los anteriores principios, todas las
emisiones radiactivas cumplen las leyes de desplazamiento radiactivo también conocidas
como las leyes de Soddy.
1. Cuando un núcleo emite una partícula alfa, su número másico decrece en cuatro
unidades y su número atómico en dos, convirtiéndose en un elemento situado dos
posiciones más a la izquierda en la tabla periódica
A
A −4
Z X→ Z − 2 Y
+α
2. Cuando un núcleo emite una partícula beta, su número másico no cambia y su
número atómico aumenta en una unidad, convirtiéndose en un elemento situado una
posición más a la derecha de la tabla periódica
A
A
Z X→ Z +1Y
+β+ν
3. Cuando un núcleo emite radiación gamma disminuye el contenido energético del
núcleo pero sigue siendo el mismo elemento.
A
A
Z X*→ Z X
+γ
La primera ley es evidente de la conservación de la carga y del número de nucleones.
La segunda ley se explica porque que un neutrón se descompone en tres partículas; un protón,
un electrón y un antineutrino (sin carga ni masa pero necesario para la conservación de la
cantidad de movimiento). El electrón y el antineutrino salen despedidos a alta velocidad del
núcleo y este experimenta un efecto de retroceso. El protón se queda dentro del núcleo
modificado. La tercera ley indica la transición a un estado de menor energía del núcleo
mediante la emisión de fotones.
Normalmente un núcleo no sufre una única desintegración, sino que se va
transformando en otros núcleos también inestables y vuelve a cambiar mediante alguna de las
emisiones vistas. Dado que las emisiones radiactivas solo pueden ser de tres tipos y,
únicamente dos de ellas tienen como resultado la transformación del núcleo, las posibles
desintegraciones nucleares están limitadas a cuatro series llamados series radiactivas. Esto
se debe a que, en cualquier emisión radiactiva, el número másico no cambia o disminuye en
cuatro unidades. Las series son secuencias de elementos por los que van pasando los
diferentes núcleos cuando se van desintegrando:
Tema 8-9
Tema 8: Interacción nuclear
Física 2º Bachillerato
•
Serie 4n, con un número másico múltiplo de 4. Serie del torio
•
Serie 4n + 1, con un número másico múltiplo de 4 más 1. Serie del neptunio
•
Serie 4n + 2, con un número másico múltiplo de 4 más 2. Serie del uranio
•
Serie 4n + 3, con un número másico múltiplo de 4 más 3. Serie del actinio
Cada serie comienza en el elemento que le da nombre y mediante los diferentes tipos
de desintegración van pasando por otros elementos e isótopos hasta acabar en algún isótopo
del plomo (206, 207 o 208) o en el bismuto 209. La figura 8.5 muestra las cuatro series
radiactivas indicando además el tipo de emisión, el periodo de semidesintegración (magnitud
que se verá en el siguiente apartado), y el porcentaje de núcleos que sufren cada
desintegración.
Serie
del
Torio
(4n)
232
Serie
del
Neptunio
(4n+1)
Th
10
α↓ 1.39·10 a
228
Ra
β↓ 6.7a
228
Ac
β↓ 6.13h
228
Th
α↓ 1.9a
224
Ra
α↓ 3.64d
220
Rn
α↓ 54.5s
216
Po (α+β) 0.16s
(∼100%) α Ë Ìβ (0.014%)
212
216
Pb
Al
10.6h β Ì Ëα 3·10–4s
212
Bi (β+α) 60m
(66.3%) βË Ìα (33.7%)
212
208
Po
Tl
–7
3·10 s αÌ Ëβ 3.1m
208
Pb
241
Pu
β↓ 10a
241
Am
α↓ 500a
237
Np
6
α↓ 2.2·10 a
233
Pa
β↓ 27.4d
233
U
5
α↓ 1.62·10 a
229
Th
3
α↓ 7·10 a
225
Ra
β↓ 14.8d
225
Ac
α↓ 10d
221
Fr
α↓ 4.8m
217
At
α↓ 0.018s
214
Bi (β+α) 47m
(96%) βË Ìα (4%)
213
208
Po
Tl
–6
4.2·10 s αÌ Ëβ 2.2m
209
Pb
β↓ 3.3h
209
Bi
Serie
del
Uranio
(4n+2)
238
U
9
α↓ 4.5·10 a
234
Th
β↓ 24.1d
234
Pa
β↓ 1.14m
234
U
5
α↓ 2.35·10 a
230
Th
4
α↓ 8·10 a
226
Ra
3
α↓ 1.62·10 a
222
Rn
α↓ 3.82d
218
Po (α+β) 3m
(99.96%) α Ë Ì β (0.4%)
214
218
Pb
At
26.8m β Ì Ëα 2s
214
Bi (β+α)19.7m
(99.96%) βË Ìα (0.4%)
214
210
Po
Tl
–4
1.4·10 s αÌ Ëβ 1.32m
210
Pb
β↓ 22a
210
Bi (β+α) 5d
(∼100%) βË Ìα (∼10−5%)
210
206
5d
Po
Tl
140d αÌ Ëβ 43.2m
206
Pb
Serie
del
Actinio
(4n+3)
U
7.07·108a
α↓
231
Th
24.6h
β↓
231
Pa
3.2·104a
α↓
227
Ac (β+α) 47m
(98.8%) β Ë Ì α (1.2%)
227
227
Th
Fr
18.9d αÌ Ëβ 21m
223
Ra
11.2d
α↓
219
Rn
3.92s
α↓
215
Po (β+α)1.8·10–3s
(∼100%) α Ë Ì β (∼5·10−4%)
211
215
Pb
At
–4
3.61m β Ì Ëα 10 s
211
Bi (β+α) 2.16m
(99.68%) β Ë Ì α (0.32%)
211
207
Po
Tl
–3
5·10 s αÌ Ëβ 4.76m
207
Pb
Figura 8.5 Series radiactivas; a=años, d=días, h=horas, m=minutos, s=segundos
Tema 8-10
235
Colegio Sagrado Corazón
8.4.4. Ley de la desintegración radiactiva; magnitudes y unidades
La desintegración en un núcleo concreto es un fenómeno que ocurre completamente al
azar. Se puede conocer la probabilidad de que ocurra en un intervalo de tiempo pero no el
instante preciso en el que se va a producir una desintegración radiactiva. Sin embargo, debido
al gran número de átomos existentes en cualquier muestra se pueden aplicar principios de
estadística con muy buena aproximación.
Si se tienen un número N de núcleos en un instante determinado t, cuando haya
transcurrido un intervalo de tiempo muy pequeño dt se habrán desintegrado una pequeña
cantidad de núcleos dN, valor que es proporcional al número de núcleos existentes N y al
tiempo transcurrido dt, luego se puede escribir:
dN = − λ ⋅ N ⋅ dt
Teniendo en cuenta siempre se pierden núcleos el signo de dN debe ser negativo. λ es
la constante de desintegración o constante radiactiva, que representa la probabilidad de
que un núcleo se desintegre en la unidad de tiempo. Un valor de λ grande representa una
elevada probabilidad de que un núcleo se desintegre y por lo tanto una muestra muy activa.
Operando la expresión anterior:
dN
= −λ ⋅ dt
N
N
∫
N0
t
dN
= − λ ⋅ dt
N
∫
0
N
t
lnN N = − λ ⋅ t 0
0
lnN − lnN0 = − λ ⋅ t
y aplicando las leyes de los logaritmos se obtiene la ley de desintegración radiactiva:
N = N0 e − λt
Siendo N0 el número de núcleos inicial, N el número de núcleos en el instante t y λ la
constante radiactiva. La representación gráfica de la desintegración radiactiva es una
exponencial decreciente. Un valor elevado de λ significa que la probabilidad de que un núcleo
sufra una desintegración es alta, y por lo tanto la muestra se desintegrará a un ritmo mayor.
La gráfica siguiente está calculada para N0=100 núcleos, tf=20s y tres valores
diferentes para λ.
Tema 8-11
Tema 8: Interacción nuclear
Física 2º Bachillerato
Desintegración Radiactiva
Núcleos restantes
120
100
80
60
40
20
λ=0.2 s–1
λ=0.5 s–1
λ=0.8 s–1
0
0
2
4
6
8
10
12
14
16
18
20
Tiempo
Figura 8.6. Evolución en el número de átomos en una muestra
Como se puede apreciar:
•
cuantos más núcleos existen en un instante determinado, mayor es el número de
desintegraciones;
cuanto mayor es el valor de λ, mayor es la probabilidad que un núcleo se desintegre
•
y, por consiguiente, el número de desintegraciones totales es mayor.
Se define el periodo de semidesintegración T1/2 (también llamado semivida) como el
tiempo necesario para que el número de núcleos disminuya hasta la mitad del valor inicial, es
decir cuando N = N0/2. Equivalentemente se puede decir que es el tiempo necesario para que
la masa disminuya a la mitad. En ese caso es fácil demostrar que;
T1/2 =
ln2
λ
Otro parámetro que no debe confundirse con el anterior es la vida media (τ) que se
mide en segundos y representa el promedio del tiempo de vida de los núcleos (la suma de las
vidas de todos dividido entre el número total de núcleos). La vida media de diferentes núcleos
puede variar entre menos de una millonésima de segundo para núcleos inestables y billones de
años para los más estables. Se puede demostrar que la vida media vale:
τ=
1
λ
Otra magnitud característica de las desintegraciones radiactivas es la actividad (A) que
representa la velocidad, en valor absoluto, a la que se producen las desintegraciones:
Tema 8-12
Colegio Sagrado Corazón
A=
dN
= λ·N
dt
La actividad depende del número de núcleos (y por lo tanto de la masa) de la muestra
por lo que varía con el tiempo. La actividad inicial es la actividad cuando no se ha producido
aún ninguna desintegración:
A 0 = λ ⋅ N0
y en cualquier instante la actividad se puede calcular de la siguiente manera:
A = A 0 e − λt
La actividad se mide en el sistema internacional en becquerels (Bq). Un Bq representa
una desintegración por segundo, lo cual no es una unidad apropiada para muestras muy
activas. En esos casos se emplea el curio, 1ci = 3'7·1010 Bq.
La ley de desintegración radiactiva ha quedado expresada en número de átomos, sin
embargo teniendo en cuenta la forma de la ecuación, ésta también se puede expresar modos:
En número de moles
En masa (Kg, g, ...)
En porcentaje
mmoles = mmoles 0 e − λt
m = m e − λt
x(%) = 100 e − λt
8.4.5. Datación mediante carbono 14
La datación mediante C-14 es un método para averiguar la antigüedad de muestras
orgánicas muy antiguas. El método consiste en comprobar la cantidad del isótopo 14 del
carbono existente en la muestra. Los seres vivos mantienen un porcentaje concreto de este
isótopo mientras permanecemos vivos. Al morir y dejar de alimentarse, no se renueva el C-14
del organismo, que sin embargo se pierde por desintegración con un periodo de
semidesintegración de 5370 años. La antigüedad de la muestra se puede calcular mediante la
expresión.
t=−
T1/2 ⎛ N
ln⎜
ln(2) ⎜⎝ N0
⎞
⎟⎟
⎠
Tema 8-13
Tema 8: Interacción nuclear
Física 2º Bachillerato
8.5. Fusión y fisión nucleares
En la mayoría de las reacciones nucleares un núcleo se transforma en otro. La energía
que se libera o se consume será la diferencia de energías entre el estado final y el estado
inicial. A la vista de la gráfica de energía de enlace por nucleón mostrada en la figura 8.7,
existen dos modos de extraer energía de una reacción nuclear:
ΔE (Fisión)
ΔE (Fusión)
Figura 8.7. Energía liberada por nucleón en las reacciones de fusión y fisión.
1. la fisión nuclear, que consiste en dividir núcleos pesados para obtener núcleos
intermedios, más ligeros que los originales y con mayor energía de enlace por nucleón;
2. la fusión nuclear, que es unir núcleos ligeros para obtener núcleos intermedios, más
pesados que los iniciales y también con mayor energía de enlace por nucleón.
En ambos casos se produce una liberación de energía correspondiente a la diferencia
de las energías de enlace por nucleón multiplicada por el número de núcleos que se
fisionan/fusionan.
Las reacciones nucleares se representan de modo parecido a las reacciones químicas.
En este tipo de reacciones se mantiene constante el número de nucleones y se debe prestar
especial atención las desintegraciones tipo β, en las que un neutrón se convierte en un protón
y un electrón. La nomenclatura de as mismas es:
A+a→X+x
o también;
A(a, x)X
donde ‘A’ es la partícula blanco ‘a’ es el proyectil y ‘X’ y ‘x’ son los productos obtenidos.
Tema 8-14
Colegio Sagrado Corazón
8.5.1. Fisión nuclear
Los núcleos más pesados se pueden descomponer para dar núcleos más ligeros.
Como se puede apreciar en la gráfica 8.7, hay una diferencia de energía de aproximadamente
1 MeV por nucleón. La energía liberada en la reacción se puede estimar multiplicando este
valor por el número de átomos que pueden intervenir en la reacción que es del orden del
número de Avogadro ≈1023, lo que da como resultado energías considerablemente altas. Las
reacciones de fisión son altamente exoenergéticas.
Figura 8.8. Esquema de reacción en cadena
La reacción de fisión se inicia con el bombardeo de los núcleos (generalmente de
uranio) con neutrones lentos. Si los neutrones son muy rápidos se producen colisiones
elásticas con los núcleos y no induce la fisión de los mismos. Los neutrones lentos son
momentáneamente absorbidos por el núcleo produciéndose a continuación la fisión. Durante la
reacción se produce pérdida de masa, que es el origen de la energía liberada. En algunas
reacciones la fisión del núcleo lleva consigo una emisión de neutrones que mantienen la
reacción, es lo que se conoce como reacción en cadena. Los neutrones emitidos suelen tener
una velocidad muy alta y deben ser frenados por otros núcleos hasta convertirse en neutrones
lentos. A la cantidad de masa necesaria para frenar los neutrones adecuadamente se le llama
masa crítica (o volumen crítico) y, para valores por debajo de ella, los neutrones no son
frenados, escapan de la muestra y no se produce la reacción en cadena.
Un ejemplo de reacción de fisión es la siguiente:
1
0n
+
235
92 U
→
135
51Sb
+
97
41Nb
+ 4 01 n
En los reactores nucleares se produce una reacción nuclear de fisión controlada, en
la que el número de neutrones lentos se regula mediante barras de control, que los absorben
en parte o en su totalidad. La energía liberada se emplea para calentar agua, que pasa a
estado de vapor y se aprovecha el cambio de volumen para mover una turbina conectada a
Tema 8-15
Tema 8: Interacción nuclear
Física 2º Bachillerato
una gigantesca bobina inmersa en un campo magnético. Ese movimiento induce una corriente
alterna en la bobina que se canaliza hasta su destino: hogares, industria, hospitales, etc.
Los inconvenientes de los reactores de fisión son los siguientes:
1. por un lado la gravedad de los accidentes en el caso de producirse, ya que,
además del efecto de una explosión termonuclear, los efectos contaminantes de
los residuos radioactivos afectarían a amplias zonas durante largos periodos de
tiempo;
2. el alto coste y peligrosidad en el transporte y almacenaje del combustible
nuclear, que generalmente es uranio enriquecido;
3. el transporte y, sobre todo, almacenaje de los residuos radiactivos, que
conservan su actividad durante cientos de años y son muy perjudiciales para la
salud y el medio ambiente;
4. el fuerte impacto ecológico de las centrales abiertas que necesitan cauces de
agua corriente en la pueden elevar significativamente la temperatura, con
importantes repercusiones en la flora y la fauna locales.
8.5.2. Fusión nuclear
Las reacciones de fusión consisten en unir núcleos ligeros para formar otros núcleos
más pesados y estables. En la figura 8.7, se puede apreciar que la cantidad de energía
liberada en un proceso típico de fusión es del orden de los 7Mev, un valor sensiblemente
mayor que en los procesos de fisión.
Esta reacción nuclear se produce de modo natural en el interior de las estrellas donde
se forman todos los átomos más pesados que el hidrógeno. Cuando una gran masa de
hidrógeno se condensa para formar una estrella, la presión en el núcleo debida la atracción
gravitatoria es tan grande que se inicia una reacción de fusión. Los núcleos de hidrógeno se
unen para formar deuterio, tritio y helio liberando grandes cantidades de energía que
mantienen la reacción. Más adelante se forman los núcleos más pesados (C, N, O, Fe...) que
son liberados al espacio cuando la estrella muere. Estos átomos forman nebulosas, polvo
cósmico, pequeños asteroides y por fin los planetas y los seres vivos.
Una de las posibles reacciones de fusión que puede aprovechar el hombre es unir
núcleos de hidrógeno (H), deuterio (2H) y tritio (3H) para formar núcleos de helio (He). Algunos
ejemplos de reacciones de fusión son:
411 H→ 42 He + 2e + γ + 25 Mev
2
2
3
1H + 1H → 2 He
Tema 8-16
+ n + 3.2Mev
Colegio Sagrado Corazón
Las ventajas de la fusión frente a la fisión son abrumadoras:
1. se produce mucha más energía;
2. los reactivos se encuentran fácilmente en la naturaleza; 30L de agua de
mar contienen 1g de deuterio capaz de liberar el equivalente a 10.000L de
gasolina;
3. el residuo de la reacción es He, que es completamente inerte y por lo tanto
se puede liberar en la atmósfera.
Los inconvenientes para el uso de las centrales nucleares de fusión son;
1. problema de los accidentes, que provocarían una explosión mucho más
devastadora que la de una central de fisión;
2. impacto ambiental, al igual que en las centrales de fisión;
3. actualmente no se puede conseguir la fusión de forma económica, es decir
cuesta más energía conseguir que se unan los núcleos que la energía que se
obtiene.
El principal problema es conseguir que los núcleos de hidrógeno, deuterio y tritio
colisionen y permanezcan unidos. Se requieren elevadas temperaturas y el confinamiento de
los núcleos en volúmenes reducidos. Es necesario el uso de las llamadas botellas magnéticas
que mantienen a los reactivos en estado de plasma de manera que tengan la suficiente energía
para fusionarse. Si se consiguiese rebajar la temperatura de activación (fusión fría) se podría
obtener una energía limpia, barata y relativamente segura.
8.6. Aplicaciones de la radiactividad y de las reacciones nucleares.
8.6.1. Utilización de los radioisótopos
Los isótopos radiactivos tienen otras muchas aplicaciones aparte de las puramente
energéticas;
•
medicina: diagnóstico y trazadores, radioterapia, esterilización de material
quirúrgico, etc.
•
industria: radiografía de piezas metálicas y de soldadura en elementos de
responsabilidad, medida precisa de espesores y niveles, trazadores, catalizadores
en reacciones químicas, irradiación de alimentos para su conservación, etc.
•
investigación: datación mediante el carbono 14, trazadores en bioquímica, etc.
•
doméstico: detectores de humos, pararrayos.
Una aplicación que desvirtúa totalmente los estudios y esfuerzos por entender y
manipular la energía nuclear es el uso militar. Las bombas atómicas usan la energía contenida
en los núcleos para la destrucción masiva de extensas zonas. Aparte de la explosión
termonuclear, dejan residuos radiactivos que producen enfermedades durante cientos o miles
de años. Las bombas lanzadas sobre Hiroshima y Nagasaki el 6 y 9 de agosto de 1945
Tema 8-17
Tema 8: Interacción nuclear
Física 2º Bachillerato
produjeron una bola de fuego de 3Km de diámetro, calcinaron totalmente la materia en un radio
de 20Km y originaron un embudo en el suelo de 100 m de profundidad y 4Km de radio, siendo
su potencia equivalente 50 megatones (50 millones de toneladas de TNT). Las bombas
causaron la muerte directa de 114.000 personas y secuelas directas o indirectas a los
descendientes que todavía perduran. Los misiles nucleares actuales son mucho más potentes
que las primeras bombas atómicas. Durante la Guerra Fría la Unión Soviética tenía armas de
destrucción masiva suficientes para arrasar toda vida sobre la tierra dos veces y los Estados
Unidos de América diez veces. Actualmente otros países como Francia, China o Corea del
Norte también disponen de armas nucleares.
8.6.2. Efectos biológicos de las radiaciones
Las radiaciones causan efectos diversos sobre los seres vivos. Los efectos de las
radiaciones dependen de varios factores:
•
del tejido u órgano irradiado;
•
del tiempo de exposición;
•
la intensidad de la radiación;
•
del tipo y energía de la radiación.
En pequeñas dosis controladas las radiaciones pueden ser beneficiosas; el ejemplo
más claro es la luz solar que produce la vitamina D en las personas. Las plantas aprovechan la
luz del sol para realizar la fotosíntesis. Determinados tipos de cáncer se pueden curar
aplicando radioterapia, que es la radiación intensa pero breve de las zonas afectadas para la
destrucción de las células cancerosas. Las radiografías permiten a los médicos observar
huesos u otras partes del organismo. Si las dosis son elevadas o prolongadas los efectos para
la salud pueden ser muy perjudiciales. Los órganos del cuerpo humano que contienen células
que se regeneran se ven afectados por las radiaciones que pueden interferir en los procesos
de división celular. Los efectos de un exceso de radiación en el cuerpo van desde las
quemaduras hasta la destrucción de las cadenas de ADN de las células con el consiguiente
riesgo de cáncer. Por último, las radiaciones más penetrantes son las emisiones gamma, por lo
que es necesario blindar los lugares donde se producen con gruesos muros de hormigón o
planchas de plomo. La radiación alfa, en cambio, es detenida fácilmente, de hecho ni siquiera
atraviesa la piel, pero si es ingerida en alimentos que permanecen en el cuerpo, como la leche
por ejemplo, puede ser muy peligrosa al estar directamente en contacto con las células.
8.7. Revisión de las interacciones fundamentales de la naturaleza. Teoría
del campo unificado.
El estudio de las fuerzas nucleares han sido posible gracias al uso de aceleradores de
partículas en los que se hacen colisionar núcleos atómicos a altas velocidades para analizar los
restos de estas colisiones. De este modo se ha descubierto que los átomos se descomponen
Tema 8-18
Colegio Sagrado Corazón
en protones, neutrones y electrones, los dos primeros a su vez están formados por quarks, de
los que se conocen seis tipos, y existen otras partículas como lo neutrinos y antineutrinos, etc.
Se ha visto en este tema que las fuerzas nucleares se ejercen en los núcleos atómicos y no se
pueden apreciar en fenómenos cotidianos. Así pues, todas las interacciones que se encuentran
en la naturaleza se pueden englobar dentro de cuatro categorías:
1. Interacción gravitatoria; todos los cuerpos experimentan fuerzas atractivas
debidas a su masa. Incluso las partículas cuya masa en reposo vale cero la
experimentan en condiciones extremas, los fotones son atraídos hacia el interior de
los agujeros negros.
2. Interacción electromagnética; las partículas cargadas experimentan fuerzas
eléctricas que pueden ser de carácter atractivo o repulsivo. Por extensión, los
cuerpos macroscópicos con desequilibrio entre el número de protones y electrones
experimentan estas fuerzas. Las fuerzas de tipo magnético se ejercen cuando las
partículas cargadas están en movimiento.
3. Interacción nuclear fuerte; estas fuerzas aparecen cuando los nucleones se
encuentran muy próximos entre sí. Son de carácter atractivo a corta distancia y
repulsivo a muy corta distancia.
4. Interacción nuclear débil; estas interacciones ocurren en la desintegración β y
son las responsables de la desintegración del protón y la emisión del electrón y el
antineutrino.
La tabla 8.2 resume las cuatro interacciones y sus principales características, alcance,
intensidad relativa, condiciones en que aparece y fenómenos relacionados. Los esfuerzos
actuales de los físicos se basan en unificar las cuatro interacciones en una sola que las
englobe a todas; es lo que se conoce como Teoría del Campo Unificado.
Intensidad relativa
Alcance
Se ejerce sobre...
Fenómenos
explicados
Nuclear fuerte
Muy fuerte (1)
Corto (10–15m)
Protones y
neutrones
Estabilidad
nuclear
Electromagnética
Fuerte (0.01)
Infinito ⎜
Protones y
electrones
Electricidad y
magnetismo
Nuclear débil
Débil (10–17)
Protones, neutrones,
electrones y
antineutrinos.
Emisión β
Materia
Gravedad,
universo.
Gravitatoria
Muy débil (10-40)
⎛ 1⎞
⎟
⎝ r2 ⎠
Muy corto (10–17m)
⎛ 1⎞
⎟
⎝ r2 ⎠
Infinito ⎜
Tabla 8.2. Comparación entre las cuatro interacciones de la naturaleza.
Tema 8-19
Tema 8: Interacción nuclear
Física 2º Bachillerato
Relación de ejercicios.
COMPOSICIÓN DEL NÚCLEO ATÓMICO: NUCLEONES
1. Defina número másico, número atómico y masa atómica. ¿Cuál de ellos caracteriza a un
elemento químico?¿Puede haber varios núcleos diferentes con el mismo número atómico y
distinto número másico? ¿Y con el mismo número másico y distinto número atómico?
Razone la respuesta y de algunos ejemplos.
2. Si se expresa 141Ba ¿queda bien definido el átomo? ¿Bastaría con indicar 141? ¿Y si sólo
se expresa Ba?
3. ¿Por qué fue necesario postular la existencia del neutrón?
4. ¿Cuántos átomos hay en 10g de Al-27? ¿Cuánto pesan 5·1025 átomos de Helio?
mAl=26.981u, mHe=4.003u.
Sol. N = 2.23·1023átomos, m = 332g
5. Deduzca el número de protones, neutrones y electrones que tiene un átomo de
27
13 Al
ESTABILIDAD NUCLEAR: ENERGÍA DE ENLACE
6.
a) ¿Cuál es la interacción responsable de la estabilidad del núcleo? Compárela con la
interacción electromagnética.
b) Comente las características de la interacción nuclear fuerte.
7. La masa de un núcleo atómico no coincide con la suma de las masas de las partículas que
lo constituyen. ¿Es mayor o menor? Justifique la respuesta.
8. Explique cualitativamente la dependencia de la estabilidad nuclear con el número másico.
Considere dos núcleos pesados X e Y de igual número másico. Si X tiene mayor energía
de enlace, ¿cuál de ellos es más estable?
9. Explique qué es el defecto de masa y calcule su valor para el isótopo 157 N . Calcule su
energía de enlace por nucleón.
c = 3·108ms–1; m(p) = 1,007276u; m(n) = 1,008665u; m(N-15) = 15,0001089u;
1u = 1,67·10–27kg.
Sol. Δm = 0.12u = 2.01·10–28Kg, Eepn = 1.20·10–12J/n.
10. Demuestra la siguiente relación 1u = 931MeV.
11. La masa del isótopo 16 del oxígeno es 15,9949u. Sabiendo que el oxigeno tiene 8 protones
calcula la energía de enlace por nucleón de un átomo de O.
m(p) = 1,007276u; m(n) = 1,008665u.
Sol. Eepn = 1.25·10–12J/n.
12. Considera la reacción nuclear siguiente:
α +105 B→136 C + p
Haz un balance energético de la reacción y explica si es endoenergética o exoenergética.
c = 3·108ms–1, mB = 10.01610u, mC = 13.00749u, mα = 4.0026u, mp = 1,007276u.
Sol. Δm = 3u = 5·10–27Kg, es exoenergética.
EMISIONES RADIACTIVAS
13. Describa las características de los procesos de emisión radiactiva alfa, beta y gamma. Uno
de ellos consiste en la emisión de electrones. ¿Cómo es posible que un núcleo emita
electrones? Razone su respuesta.
Tema 8-20
Colegio Sagrado Corazón
14. ¿Qué cambios experimenta un núcleo atómico al emitir una partícula alfa? ¿Qué sucedería
si un núcleo emitiese una partícula alfa y después dos partículas beta?
15. El 210
83 Bi emite una partícula beta y después una partícula alfa. Indica los isótopos que se
forman tras ambas emisiones.
16. Si se bombardea Li-6 con un neutrón y se emite una partícula alfa ¿cuál es el residuo?
17. Complete las siguientes ecuaciones de reacciones nucleares, indicando en cada caso las
características de X:
9
4
12
4 Be + 2 He→ 6 C + X
27
1
4
13 Al+ 0 n→ 2 He +
X
18. Indica cuántas emisiones alfa y beta hacen falta para pasar de 235U a 207Pb.
19. Completa las ecuaciones de desintegraciones nucleares siguientes:
214
210
→ 209
84 Po→ 82 Pb +
83 Bi + α
234
234
90 X → 91Y
+
210
85 At
→
+γ
20. Razone cuáles de las siguientes reacciones nucleares son posibles:
1
3
4
1H+ 2 He→ 2 He
224
219
4
88 Ra→ 86 Rn+ 2 He
4
27
30
1
2 He + 13 Al→ 15 P + 0 n
21. Algunos átomos de nitrógeno ( 147 N ) atmosférico chocan con un neutrón y se transforman
en carbono ( 146 C ) que, por emisión β, se convierte de nuevo en nitrógeno. Escriba las
correspondientes reacciones nucleares.
22. El
12
5B
se desintegra radiactivamente en dos etapas: en la primera el núcleo resultante es
12
6C *
(* = estado excitado) y en la segunda el 126 C * se desexcita, dando 126 C (estado
fundamental). Escriba los procesos de cada etapa, determinando razonadamente el tipo de
radiación emitida en cada caso.
23. Complete las siguientes reacciones nucleares:
59
27 Co
+ ____ →
124
51 Sb
→
124
52Te
56
4
25 Mn+ 2 H
+ ____
24. Explique en qué se diferencian las reacciones nucleares de las reacciones químicas
ordinarias.
Tema 8-21
Tema 8: Interacción nuclear
Física 2º Bachillerato
LEY DE DESINTEGRACIÓN RADIACTIVA
25.
a) Enuncie la ley de desintegración radiactiva e indique el significado físico de cada uno
de los parámetros que aparecen en ella.
b) ¿Por qué un isótopo radiactivo de período de semidesintegración muy corto (por
ejemplo, dos horas) no puede encontrarse en estado natural y debe ser producido
artificialmente.
c) Supuesto que pudiéramos aislar un átomo de la muestra anterior discuta, en función
del parámetro apropiado, si cabe esperar que su núcleo se desintegre pronto, tarde o
nunca.
26. Un núcleo tiene un periodo de semidesintegración de un año ¿Significa eso que en dos
años la masa habrá desaparecido completamente?
27. A partir de la ecuación de desintegración demuestra el valor de T1/2.
28. Contesta si la actividad depende o no depende de:
a) el tiempo;
b) la masa;
c) la constante radiactiva;
d) el número de átomos.
29. Dos muestras A y B del mismo elemento radiactivo se preparan de manera que la muestra
A tiene doble actividad que la B.
a) Razone si ambas muestras tienen el mismo o distinto período de desintegración.
b) ¿Cuál es la razón entre las actividades de las muestras después de haber trascurrido
cinco períodos?
30. Justifique la veracidad o falsedad de las siguientes afirmaciones:
a) Cuanto mayor es el período de semidesintegración de un material, más deprisa se
desintegra.
b) En general, los núcleos estables tienen más neutrones que protones.
31. Indique el significado de: período de semidesintegración, constante radiactiva y actividad.
¿Cómo cambiaría una muestra de un radionúclido transcurridos tres períodos de
semidesintegración?
32. ¿Qué porcentaje de la cantidad inicial de un cierto elemento se ha desintegrado
transcurridos cuatro periodos de semidesintegración? ¿Cuánto queda?
Sol. 93.75% desintegrado, 6.25% queda.
33. ¿Cuánto valdrá la actividad de una muestra a las 60h si la actividad inicial es 4000 desint/s
y el periodo de semidesintegración vale 15h?
Sol. A = 250 desint/s
34. Una muestra de 6e15 átomos tiene una vida media de 20días. ¿Cuántos átomos quedarán
de la muestra tras un año?
Sol. 7.12·107 átomos.
35. ¿Cuánto tarda una muestra de T1/2 = 5 días en disminuir su masa al 25%?, ¿y al 1%?
Sol. 10 días, 33.22días.
36. Se tiene una muestra de Rn-222 de 10g con T1/2=3.82d.
a) ¿Cuánto queda después de 3.82 días?, ¿7.64 días?, ¿11.46 días?
b) ¿Cuánto queda después de 5 días?, ¿10 días?, ¿15 días?
Sol. a) 5g, 2.5g, 1.25g; b) 4.04g, 1.63g, 0.66d
37. Una muestra de isótopo radiactivo recién obtenida tiene una actividad de 84s–1 y, al cabo
de 30 días, su actividad es de 6s–1.
a) Explique si los datos anteriores dependen del tamaño de la muestra.
b) Calcule la constante de desintegración y el porcentaje de núcleos que se han
desintegrado después de 11 días.
Sol. b) λ = 0.08797s–1, 62%.
Tema 8-22
Colegio Sagrado Corazón
38. El período de semidesintegración del Ra-226 es de 1620 años.
a) Explique qué es la actividad y determine su valor para 1g de Ra-226.
b) Calcule el tiempo necesario para que la actividad de una muestra de Ra-226 quede
reducida a un dieciseisavo de su valor original.
NA = 6,02·1023mol–1
Sol. a) 3.62·1010 desint/s; b) t = 6480 años.
39. El 244
94 Pu se desintegra, emitiendo partículas alfa, con un periodo de semidesintegración de
45,7 días.
a) Escriba la reacción de desintegración y determine razonadamente el número másico y
el número atómico del elemento resultante.
b) Calcule el tiempo que debe transcurrir para que la actividad de una muestra de dicho
núclido se reduzca a la octava parte.
Sol. b) t = 137.1 días
40. El núcleo radiactivo 235
92 U se desintegra, emitiendo partículas alfa, con un período de
semidesintegración de 72 años.
a) Escriba la ecuación del proceso de desintegración y determine razonadamente el
número másico y el número atómico del núcleo resultante.
b) Calcule el tiempo que debe transcurrir para que su masa se reduzca al 75% de la masa
original.
Sol. b) t = 29.88 años.
222
41. El 226
88 Ra se desintegra radiactivamente para dar 86 Rn .
a) Indique el tipo de emisión radiactiva y escriba la correspondiente ecuación.
b) Calcule la energía liberada en el proceso.
c = 3·108ms–1; m(Ra) = 225,9771u; m(Rn) = 221,9703u; m(He) = 4,0026u;
1u = 1,67·10–27kg
Sol. b) E = 6.31·10–13J.
42. Los restos de animales recientes contienen mayor proporción de 146 C que los restos de
animales antiguos. ¿A qué se debe este hecho y qué aplicación tiene?
43. ¿Cuánto tiempo hace que murió una planta fosilizada a la que le queda el 12.5% de C-14
que tenía cuando estuvo viva?.
T1/2 (C-14) = 5370 años
Sol. t = 16110 años.
44. El isótopo del hidrógeno denominado tritio ( 31H ) es inestable (T1/2= 12,5 años) y se
desintegra con emisión de una partícula beta. Del análisis de una muestra tomada de una
botella de agua mineral se obtiene que la actividad debida al tritio es el 92% de la que
presenta el agua en el manantial de origen.
a) Escriba la correspondiente reacción nuclear.
b) Determine el tiempo que lleva embotellada el agua de la muestra.
Sol. b) t = 1.5 años.
45. En una muestra de la madera con que está hecho un sarcófago antiguo ocurren 13536
desintegraciones de C-14 por gramo en un día, mientras que en una muestra de un gramo
de la misma madera recién cortada ocurren 920 desintegraciones por hora. El período de
semidesintegración del 14C es de 5370 años.
a) Establezca la edad del sarcófago.
b) Determine la actividad de la muestra del sarcófago dentro de 1000 años.
Sol. a) 3791 años; b) A = 0.1377 desint/s.
FUSIÓN Y FISIÓN NUCLEARES
46. Dibuje de forma aproximada la gráfica que representa la energía de enlace por nucleón en
función del número másico e indique qué puede deducirse de ella en relación con la
estabilidad de los núcleos. Razone, a partir de la gráfica, cuál de los dos procesos, la fusión
o la fisión nucleares, proporciona mayor energía por nucleón.
Tema 8-23
Tema 8: Interacción nuclear
Física 2º Bachillerato
47. ¿Qué ventaja presenta usar neutrones para bombardear núcleos atómicos? ¿Qué ventaja
tienen los protones?
48. Sea el siguiente proceso nuclear:
y
235
140
x U + n→ 54 Xe+ 38 Z
+ 3n
Establece los valores de X, Y y Z (usa una tabla periódica). Explica si se trata de un
proceso adecuado para una reacción nuclear en cadena.
49. Comenta las características de las reacciones de fusión siguientes indicando
razonadamente cuál te parece más adecuada para una central nuclear. Sugerencia:
plantea las ventajas e inconvenientes de cada una.
411H→ 42 He + 2e + γ + 25 Mev
2
2
3
1H + 1H → 2 He
+ n + 3.2Mev
50. En la reacción de fisión del 235
92 U , éste captura un neutrón y se produce un isótopo del Kr,
de número másico 92; un isótopo del Ba, cuyo número atómico es 56 y 3 neutrones.
Escriba la reacción nuclear y determine razonadamente el número atómico del Kr y el
número másico del Ba.
51. En la bomba de hidrógeno se produce una reacción termonuclear en la que se forma helio
a partir de deuterio y de tritio.
a) Escriba la reacción nuclear.
b) Calcule la energía liberada en la formación de un átomo de helio y la energía de enlace
por nucleón del helio.
c = 3·108ms–1 ; m( 42 He ) = 4,0026u ; m( 31H ) = 3,0170u; m( 21H ) = 2,0141u; mp = 1,007276u;
mn = 1,008665u; 1u = 1,67·10–27kg.
Sol. b) Eform = 2.98·10–12J, Eepn = 1.10·10–12J/n.
52. En la explosión de una bomba de hidrógeno se produce la reacción:
2
3
4
1
1 H+ 1 H→ 2 He+ 0 n
Calcule:
a) El defecto de masa entre el He y sus partículas constituyentes.
b) La energía liberada en la formación de 10g de helio según la reacción.
m(H-2) = 2,0141u ; m(H-3) = 3,0170u; m(He-4) = 4,0026u; m(n) = 1,0087u; mp = 1,0073u
c = 3·108ms–1; 1u = 1,66·10–27kg
Sol. a) Δm = 0.029u = 4.91·10–29Kg, b) E10g = 4.48·1012J.
53. En una reacción nuclear se produce un defecto de masa de 0,2148u por cada núcleo de
U-235 fisionado.
a) Calcule la energía liberada en la fisión de 23,5 g de 235-U.
b) Si se producen 1020 reacciones idénticas por minuto, ¿cuál será la potencia disponible?
1u = 1,67·10–27kg; c = 3·108ms–1; NA = 6,02·1023 mol–1
Sol. a) E = 1.94·1012J; b) P = 5.38·107w = 53.8Mw
54. Calcule la energía liberada en la reacción de fusión:
2
2
4
1H + 1H → 2 He
8
–1
–27
c = 3 ·10 ms ; 1u = 1,66·10 kg; m(He-4) = 4,0026u ; m(H-2) = 2,0141u
Sol. E = 3.85·10–12J
55. Suponga una central nuclear en la que se produjera energía a partir de la siguiente
reacción nuclear de fusión:
4 42 He→168 O
a) Determine la energía que se produciría por cada kilogramo de helio que se fusionase.
b) Calcule en cuál de los dos núcleos (He-4 y O-16) anteriores es mayor la energía de
enlace por nucleón.
c = 3·108ms–1; 1u = 1,66·10–27kg; m(He-4) = 4,0026u; m(O-16) = 15,9950 u
Tema 8-24
Colegio Sagrado Corazón
Sol. a) E = 8.71·1013J; b) Eepn He = 1.10·10–12J/n, Eepn O = 1.25·10–12J/n.
56. En el proceso nuclear siguiente determina la cantidad diaria de tritio que hace falta para
obtener una potencia de 2000MW, si el rendimiento de la central es del 20%, la energía
liberada en la reacción son 17.6 MeV y la masa atómica del tritio son 3.017 umas.
2
3
4
1 H+ 1 H→ 2 He
+n
Sol. 1.54Kg/día de H-3.
57. Considere la reacción nuclear:
235
1
133
99
1
92 U + 0 n →
51Sb + 41Nb + 4 0 n
a) Explique de qué tipo de reacción se trata y determine la energía liberada por átomo de
Uranio.
12
b) ¿Qué cantidad de 235
95 U se necesita para producir 3.6·10 J ?
c = 3·108ms–1; NA = 6,02·1023mol–1; m(U) = 235,128u;
m(Sb) = 132,942u; m(Nb) = 98,932u; m(n) = 1,0086u; 1u = 1,66·10–27kg
Sol. a) E = 3.43·10–11J; b) m = 41g = 0.041Kg.
Tema 8-25