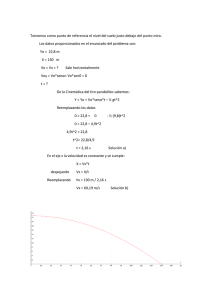
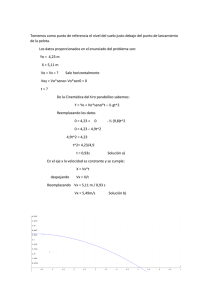
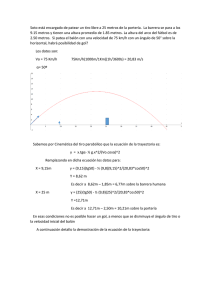
Ymax = Vo^2
Anuncio
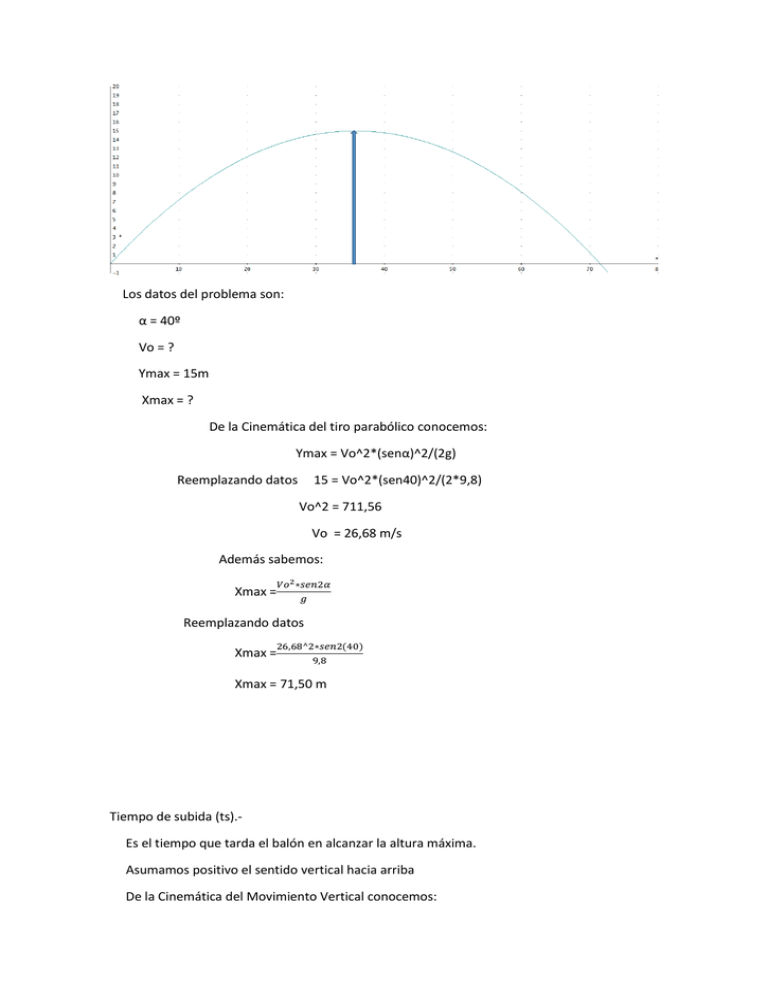
Los datos del problema son: α = 40º Vo = ? Ymax = 15m Xmax = ? De la Cinemática del tiro parabólico conocemos: Ymax = Vo^2*(senα)^2/(2g) Reemplazando datos 15 = Vo^2*(sen40)^2/(2*9,8) Vo^2 = 711,56 Vo = 26,68 m/s Además sabemos: 𝑉𝑜2 ∗𝑠𝑒𝑛2𝛼 𝑔 Xmax = Reemplazando datos 26,68^2∗𝑠𝑒𝑛2(40) 9,8 Xmax = Xmax = 71,50 m Tiempo de subida (ts).Es el tiempo que tarda el balón en alcanzar la altura máxima. Asumamos positivo el sentido vertical hacia arriba De la Cinemática del Movimiento Vertical conocemos: Vy = Voy – gt Cuando el balón llega a su punto más alto ymax su velocidad vertical es cero Vy = 0 y el tiempo que tarda en alcanzarlo es ts. Reemplazando estos valores en (1) y despejando ts: 0 = Vo*senα- g*ts ts= Vo∗senα g (1) Tiempo de vuelo (tv).- El tiempo de vuelo es el tiempo que ha permanecido el balón en el aire y por simetría es igual a: tv = 2*ts tv = 2Vo∗senα g (2) En el eje x el movimiento es uniforme MU x = Vox* t x = Vo*cosα *t (3) Cuando t =tv ----- x= Xmax Xmax = Vo*cosα *tv Xmax = Vo*cosα *2Vo*senα/g Xmax = Vo^2 *2senαcosα/g 𝑉𝑜2 ∗𝑠𝑒𝑛2𝛼 𝑔 Xmax = Pero sen2α= 2senαcosα (4) La altura máxima Ymax.- En el punto más alto de la trayectoria la componente vertical de la velocidad es cero y su altura se conoce como Ymax. De la cinemática del tiro parabólico sabemos: y = Vo*senα*t – ½ gt^2 reemplazamos ts (1) en esta última expresión Ymax = Vo*senα*Vo*senα/g – ½ g(Vo*senα/g)^2 Ymax = Vo^2*(senα)^2/g – ½ Vo^2*(senα)^2/g Ymax = Vo^2*(senα)^2/(2g) (5)