Ejercicios de circuitos magnéticos

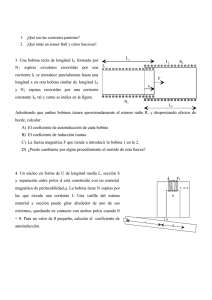
Problemas Circuitos Magnéticos
Página 1 de 6
Problemas de Circuitos Magnéticos
1-1. Determinar la intensidad en corriente continua que debe circular por la bobina de
la Fig. 1-35 para que en la rama central del nuc1eo exista un flujo de 7,5 X 10-4 weber.
Despréciese la dispersión magnética, el efecto de bordes y la reluctancia del hierro.
Fig. 1-35. Reactancia con entrehierro.
Si se alimenta la bobina con corriente alterna senoidal de 120 V de tensión eficaz, en
lugar de hacerlo con corriente continua como en el caso anterior. Determínense las
pérdidas en el hierro y el valor eficaz de la corriente magnetizante. Despréciense la
influencia de los armónicos y la caída de tensión en la resistencia de la bobina.
1-2. Las bobinas del circuito magnético de la Fig. 1-36 se conectan en serie de tal forma
que las f.m.m. en A y B tienden ambas a dirigir el flujo hacia el ramal central C en la
misma dirección. El material es acero y el volumen útil ocupado por el (factor de relleno)
es de 0,94 del volumen total. Despréciese el efecto de bordes y la dispersión.
Sección recta de A y de B = 1250 mm2. Secci6n recta de C = 2500 mm2. Longitud de la
rama A = 150 mm. Longitud de la rama B = 150mm. Longitud de la rama C = 50 mm.
Entrehierro = 3,7 mm.
Fig. 1-36. Circuito magnético del problema 1-2
a. Determinar la intensidad en ampere necesaria para que la densidad de flujo sea de 0,6
weber/m2
Prof. Alexander Bueno
07-May-04
Problemas Circuitos Magnéticos
Página 2 de 6
b. ¿Cual será la energía en joule almacenada en el campo magnético del entrehierro?
1-3. A un devanado sin resistencia, de 1000 espiras, bobinado sobre un núcleo de hierro
cerrado de 10-3 m2 de sección recta, se le aplica una tensión alterna de forma cuadrada de
frecuencia 50 Hz. Los serniciclos positivo y negativo son iguales y de amplitud E volt.
a. Trazar las curvas de tensiones y flujos en función del tiempo.
b. Hallese el máximo valor permisible para E para que la densidad máxima de flujo no
supere 1,00 weber/m2.
1-4. Los datos de la mitad superior de la curva de histéresis simétrica correspondiente al
núcleo del problema 1-3 son los siguientes:
B webers/m2
0
0.2
0.4
0.6
0.7
0.8
0.9
1.0
H
ampvueltas/m
48
52
58
73
85
103
135
193
0.9
5
80
0.9
0.8
0.7
0.6
0.4
0.2
0
42
2
-18
-29
-40
-45
-48
La longitud media del recorrido del flujo en el núcleo es de 0,30 m.
Hallense gráficamente las pérdidas por histéresis, expresadas en watt, siendo la densidad
máxima de flujo de 1,00 weber/m2 y la frecuencia 50 Hz.
1.1. Calcular la intensidad que debe aplicarse a la bobina del circuito magnético de la
Figura P.l.l. para establecer en la columna derecha un flujo de 10-3Wb. La permeabilidad
relativa se supone que es constante en todos los puntos y de valor µr.=400, Y la sección S
= 10 cm2 es la misma en toda la estructura, excepto en la columna izquierda, que vale 20
cm2. La longitud l es igual a 10 cm. Calcular también el flujo en el brazo central.
Figura P.1.l.
[Resp.: I= 9,95 A; Φ= 2,2 mWb.]
1.2 Un circuito magnético tiene una sección uniforme de 8 cm2 y una longitud magnética
media igual a 0,3 metros. Si la curva de magnetizaci6n del material viene expresada
aproximadamente por la ecuación:
1.6 H
B=
B: Teslas; H: Av/m
77 + H
Prof. Alexander Bueno
07-May-04
Problemas Circuitos Magnéticos
Página 3 de 6
Calcular la c.c. en amperios que debe introducirse en la bobina de excitación, que tiene
100 espiras, para producir un flujo en el núcleo de 8 . 10-4Wb.
[Resp.: 0,42 A]
1.3. Calcular la corriente necesaria en la bobina de la Figura P.1.2 para producir una
densidad de flujo en el entrehierro igual a 0,8 Teslas. El núcleo esta hecho de un material
cuya curva de imanaci6n viene dada por:
1.6 H
B=
B: Teslas; H: Av/m
75 + H
[Resp.: 6,83 A]
Figura P.I.2.
1.4. En la estructura magnética mostrada en la Figura P. 1.3, la densidad de flujo en el
ntrehierro de la derecha es de 1 Wb/m2. El núcleo está hecho de un material cuya curva
de imanación viene dada por:
1.5 H
B=
B: Teslas; H: Av/m
1000 + H
Figura P.l.3.
la longitud l =10 cm y la sección transversal es uniforme y vale 5 cm2. Calcular las
corrientes I 1 e I 2 que deben circular por las bobinas para que el flujo en el entrehierro
izquierdo sea nulo. [Resp.: I1 ≈ 28 A; I 2 ≈ 8 A]
Prof. Alexander Bueno
07-May-04
Problemas Circuitos Magnéticos
Página 4 de 6
1.5. La estructura magnética mostrada en la Figura P. 1.4 está construida con un material
cuya curva de imanación se expresa por:
1.5 H
B=
B: Teslas; H: Av/m
100 + H
Figura P.l.4.
La longitud de la trayectoria magnética media en el núcleo es igual a 0,75 m. Las
medidas de la sección transversal son de 6 x 8 cm2.La longitud del entrehierro es de 2
mm y el flujo en el mismo es igual a 4 mWb (en el sentido indicado en la Fig. P.1.4).
Determinar el número de espiras de la bobina B. [Resp.: NB ≈ 1.237 espiras.]
1.6. EI núcleo magnético mostrado en la Figura P.1.5 tiene una secci6n transversal
uniforme igual a 100 cm2. La bobina A tiene 1.000 espiras, circulando una c.c. de 0,5 A
en la dirección indicada. Determinar la corriente IB, para conseguir un flujo nulo en el
brazo central. La permeabilidad relativa es µ,= 200. [Resp.: 18= 1,25 A]
Figura P.1.5.
Prof. Alexander Bueno
07-May-04
Problemas Circuitos Magnéticos
Página 5 de 6
1.7. EI circuito magnetico de la Figura P.1.6 esta construido con un material, cuya curva
de magnetizaci6n viene dada por:
1.5 H
B=
B: Teslas; H: Av/m
50 + H
Figura P.l.6.
La sección de la columna central vale 50 cm2 y en el resto es uniforme y de valor 25 cm2.
Si N1 =N2 =360 espiras, calcular el valor de I1 = I2 para producir un flujo de 5 . 10-3Wb
en el entrehierro. [Resp.: 11,32 A]
1.8. La estructura magnética de la Figura P.1.7 esta fabricada con dos tipos de materiales,
cuyas curvas de magnetización vienen expresadas por las ecuaciones:
1.1 H 1
2.1 H 2
B=
, B=
B: Teslas; H: Av/m
5000 + H 1
2000 + H 2
Figura P.1.7.
Calcular la intensidad I que debe circular por la bobina para producir un flujo de 1,5.10-4
Wb, si la sección es uniforme y vale 15 cm2. [Resp.: 1 A.]
1.9. Una estructura magnética homogénea tiene una longitud magnética media igual a 50
cm; y tiene una sección uniforme de 10 cm2. Si la bobina tiene 100 espiras y la curva de
magnetización viene expresada por:
Prof. Alexander Bueno
07-May-04
Problemas Circuitos Magnéticos
Página 6 de 6
1.5 H
B: Teslas; H: Av/m
100 + H
Cuando circula por la bobina una intensidad de 0,1 A se pide el valor del coeficiente de
autoinducción calculado por los tres procedimientos siguientes: a) Empleando la formula:
L = N dΦ di . b) Utilizando la expresion: L = N Φ i .c) Calculando la energía magnética.
[Resp.: a) 2,08 H; b) 2,5 H; c) 2,34 H.]
B=
1.10. Una bobina con núcleo de hierro, tiene 500 espiras, siendo su resistencia
despreciable. La sección del núcleo es uniforme y vale 25 cm2, siendo la longitud
magnética media igual a 80 cm. La curva de imanación del material es:
2H
B=
, B: Teslas; H: A.v/m
150 + H
Si la tensión aplicada es alterna y de 220 V eficaces y la frecuencia es de 50 Hz, calcular:
a) Circuito equivalente de la bobina. b) Corriente de excitación.
NOTA: Se conoce, por la información proporcionada por el constructor, que a la tensión
nominal de 220 V Las perdidas en el núcleo son de 5 W/kg. El peso específico del
material es igual a 7,8 kg/dm3. [Resp.: a) RFe= 620,5Ω ; Xµ= 1.972 Ω; b) 0,372 A.]
Bibliografía
• Jesús Fraile Mora. “Máquinas Eléctricas”. Quinta Edición. McGraw
Hill 2003.
• Kingsley, Kusko y Fitzgerald. “Teoría y Análisis de las Máquinas
Eléctricas”. Segunda Edición. Editorial Hispano Europea. Barcelona.
España. 1984.
Prof. Alexander Bueno
07-May-04