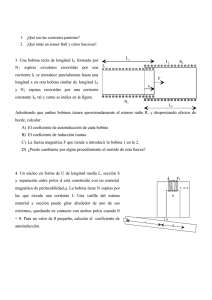
Características de una Inductancia en un Circuito RL SERIE

Laboratorio de Electricidad
PRACTICA - 10
CARACTERÍSTICAS DE UNA INDUCTANCIA EN UN CIRCUITO RL SERIE
I - Finalidades
1.- Estudiar el efecto en un circuito de alterna, de una inductancia y una resistencia conectadas en
serie.
2.- Determinar la reactancia inductiva (XL) y la autoinducción (L) de una inductancia en las
condiciones de funcionamiento.
3.- Comprobar el desfase existente entre la tensión y la corriente en un circuito RL.
II - Material necesario
1
1
1
1
1
1
1
1
1
2
1
1
Panel universal de conexión P-110
Fuente de alimentación: Tensión alterna aislada, 6'3 V (eficaces) 50 Hz.
Multímetro electrónico digital
Multímetro electrónico analógico
Osciloscopio
Resistencia carbón
4'7 K? , 1/2 W
Resistencia carbón
250 ? ,
1W
Inductancia (self) T-7
Interruptor a bola
Puentes P-442
Cable, 600 mm, color rojo
Cable, 600 mm, color negro
Nº ________
Nº ________
Nº ________
Nº ________
III - Generalidades
En los circuitos de continua, las resistencias limitan la corriente. De igual manera, las resistencias
se oponen al paso de la misma en los circuitos de alterna. Existen, además, otros componentes,
denominados reactivos, que se oponen al paso de la corriente en los circuitos de alterna: las
inductancias (bobinas de autoinducción) y los condensadores. Los efectos reactivos de estos
componentes no pueden ser determinados directamente por medio del óhmetro.
La propiedad que tiene una bobina de oponerse a cualquier variación de la corriente que la atraviesa,
es la denominada autoinducción (L). La unidad de autoinducción es el henry.
Para determinar la corriente alterna que circula por una bobina, habrá pues, que hallar la
autoinducción, la misma, además, de su resistencia en corriente continua.
Práctica nº 10
Pág. 59
Laboratorio de Electricidad
La oposición que presenta una inductancia a la corriente alterna se denomina reactancia inductiva,
su valor se expresa en ohmios y viene dada por la fórmula:
X L ? ? ? L ? 2 ? ? f ?L
(1)
donde 2? es constante (6'28 aprox.); f es la frecuencia de la tensión (y la corriente) expresada en Hz
y L es la autoinducción en henry.
De la fórmula (1) deducimos fácilmente que para la corriente continua (donde f=0), la XL de una
inductancia es cero. De esta forma, la única oposición que una bobina ofrece al paso de la corriente
continua es su resistencia, la cual puede medirse directamente con el óhmetro.
De (1) se deduce asimismo, que la XL de una inductancia es directamente proporcional a la
frecuencia de la corriente alterna que la atraviesa, es decir, la reactancia aumenta o disminuye en
función de la frecuencia.
La ley de Ohm se hace extensible a los circuitos de alterna. Sea el circuito de la figura, suponiendo
que la bobina L tenga una resistencia nula, la corriente en el circuito estará limitada únicamente por
la XL de la misma.
U
6,3 V ef.
50 Hz
I?
En este caso,
L
10 H
U
XL
y siendo L=10 H, f=50 Hz y V=6'3 V
I?
6' 3
6' 3
?
? 0' 002 A ? 2mA
2 ? ?50 ?10 3140
Si la bobina está en serie con una resistencia de, por ejemplo, 5 K? , el valor de la corriente será
inferior a 2 mA. En el circuito de la siguiente figura se aprecia la disposición de la inductancia y la
resistencia en serie.
U
6,3 V ef.
50 Hz
L
10 H
R
5 K?
Práctica nº 10
Pág. 60
Laboratorio de Electricidad
En este circuito la corriente viene dada por:
I?
U
Z
(2)
donde la impedancia Z, es la oposición total que presentan a la corriente la XL y la R del circuito. El
valor de Z viene dado por la fórmula:
Z?
R2 ? X L 2
(3)
La expresión (3), lleva implícita que la dependencia entre R y XL no es simplemente aritmética. Es
decir, R y XL son las componentes vectoriales de Z (vector resultante).
? =2 ? f
?
Z
U
XL
UL
UR
R
0
0
Las tensiones existentes en bornes de L(UL) y R(UR), pueden determinarse utilizando las fórmulas:
U
?X L
Z
U
U R ? ?R
Z
UL ?
(4)
(5)
Idénticamente, UL y UR no pueden sumarse aritméticamente para obtener la tensión aplicada U. La
dependencia entre estos valores viene dada por:
U ? U R2 ? U L2
(6)
Si la corriente I y la tensión U son conocidas, es posible determinar la impedancia total Z del circuito,
por sustitución en la expresión (2). Si se conoce, además UL, es decir, la tensión en bornes de L, es
posible determinar ZL sustituyendo UL e I en la fórmula:
ZL ?
UL
I
(7)
Suponiendo que el valor de la resistencia pura de la bobina sea muy pequeño comparado con el de
ZL, ésta será prácticamente igual a XL, y la fórmula (7) se transforma en:
XL ?
UL
I
(8)
Una vez determinada XL es fácil hallar L, sustituyendo los valores conocidos de XL y f:
L?
Práctica nº 10
XL
2? ? f
(9)
Pág. 61
Laboratorio de Electricidad
En esta práctica determinaremos la corriente I en un circuito RL. Dicha corriente puede medirse
utilizando un miliamperímetro de alterna. Puede también hallarse fácilmente, midiendo la tensión UR
existente en bornes de R y luego sustituyendo los valores conocidos de UR y R en la fórmula:
I?
UR
R
(10)
Determinado el valor de I, podemos hallar XL, midiendo la tensión UL en bornes de la bobina de
autoinducción y aplicando la fórmula (8), en el supuesto de que Z L ? X L .
En esta práctica efectuaremos medidas de tensión utilizando un voltímetro electrónico y un
osciloscopio. De ellos, este último es el que menos efecto de carga produce en el circuito.
Las lecturas de los valores cresta a cresta tomados con el osciloscopio habrá que convertirlas en
valores eficaces, aplicando la relación:
Vef ?
U CC U CC
?
2 2 2' 82
IV - Procedimiento
1.- Medir y anotar el valor de la resistencia RL de la bobina de autoinducción cuya inductancia L es
desconocida.
2.- Conectar el circuito de la figura (lámina 10.1). Ajustar la tensión de alimentación a 6'3 Vef.
S
A
T7
RL
U
6,3 V ef.
50 Hz
L
250 ?
R
C
4'7 K?
B
3.- Construir una tabla con tres columnas: Tensión medida con voltímetro (valor eficaz), tensión
medida con osciloscopio (cresta a cresta) y valor cresta a cresta convertido en eficaz.
4.- Medir con el multímetro y anotar en la tabla el valor eficaz de las tensiones en bornes de R (UR),
L (UL) y la tensión aplicada al circuito (U).
5.- Medir con el osciloscopio las tensiones cresta a cresta UR, UL,y U. Anotar sus valores en la
tabla. Dibujar la tensión U y medir la frecuencia.
6.- Convertir los valores cresta a cresta en valores eficaces y anotarlos en la columna
correspondiente.
Práctica nº 10
Pág. 62
Laboratorio de Electricidad
7.- Aplicando la fórmula (10) calcular la corriente en el circuito. Con la fórmula (8) calcular la
reactancia inductiva XL y despejando L en la fórmula (1) obtener el valor de la autoinducción de
la bobina.
8.- En el punto anterior se ha calculado el valor de L considerando que la inductancia es pura
despreciando su resistencia. En el punto 1 se ha comprobado que una inductancia real tiene un
valor de resistencia RL que hay que tener en cuenta. En este caso después de obtener el valor
de la corriente con la fórmula (10), calcular el valor de la impedancia de la bobina ZL con la
fórmula (7) y despejar L de la fórmula:
ZL ?
R2L ? X L ?
2
b g
R2L ? ? ?L
2
9.- Conectar una sonda del osciloscopio para medir la tensión de alimentación U (entre A y C), y la
otra sonda para medir la tensión en la resistencia UR (entre B y C). Dibujar un periodo completo
de cada forma de onda.
10.- Con las formas de onda anteriores calcular el desfase existente entre ambas.
11.- Desconectar la bobina del circuito y reemplazarla por una resistencia cuyo valor sea el mismo
que el de la bobina (valor medido en la operación nº 1).
12.- Repetir las operaciones nº 9, 10 y 11.
Práctica nº 10
Pág. 63
Laboratorio de Electricidad
Volts/Div=
Time/Div=
Volts/Div=
Time/Div=
Volts/Div=
Time/Div=
Práctica nº 10
Volts/Div=
Time/Div=
Volts/Div=
Time/Div=
Volts/Div=
Time/Div=
Pág. 64
Laboratorio de Electricidad
Práctica nº 10
Pág. 65