Una empresa se dedica a la producción de dos tipos de tejidos A y
Anuncio

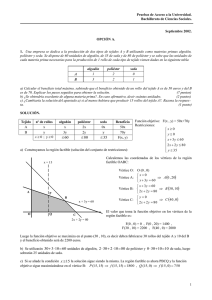
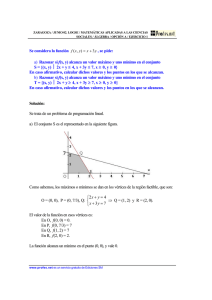
ZARAGOZA / SEPTIEMBRE 02. LOGSE / MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES / ÁLGEBRA / OPCIÓN A / EJERCICIO 1 Una empresa se dedica a la producción de dos tipos de tejidos A y B utilizando como materias primas, algodón, poliéster y seda. Si dispone de 60 unidades de algodón, de 35 de seda y de 80 de poliéster y se sabe que las unidades de cada materia prima necesarias para la producción de 1 rollo de cada tipo de tejido vienen dadas en la siguiente tabla: algodón poliéster seda A 1 2 0 B 3 2 1 a) Calcular el beneficio total máximo, sabiendo que el beneficio obtenido de un rollo de tejido A es de 50 euros y del B es de 70. Explicar los pasos obtenidos para obtener la solución. b) ¿Se obtendrá excedente de alguna materia prima? En caso afirmativo, decir cuántas unidades. c) ¿Cambiaría la solución del apartado a) si al menos hubiera que producir 15 rollos de tejido A? Razonar la respuesta. Solución: Con los datos anteriores se obtiene: Cantidad Algodón A x x B y 3y Disponibilidades 60 Poliéster 2x 2y 80 Seda 0 y 35 El objetivo es maximizar el beneficio. Esto es: Maximizar B(x, y) = 50x + 70y restringido por: x + 3y ≤ 60 (unidades de algodón) 2x + 2y ≤ 80 (unidades de poliéster) y ≤ 35 (unidades de seda) x ≥ 0; y ≥ 0 Estas restricciones generan la región factible dada en la siguiente figura. www.profes.net es un servicio gratuito de Ediciones SM Beneficio 50x 70y ZARAGOZA / SEPTIEMBRE 02. LOGSE / MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES / ÁLGEBRA / OPCIÓN A / EJERCICIO 1 Los vértices son: x + 3 y = 60 ⇒ Q = (30, 10) y R = (40, 0). O = (0, 0), P = (0, 20), Q: 2 x + 2 y = 80 Como sabemos, la solución buscada se encuentra en alguno de esos vértices. Los beneficios para esos niveles de producción son: En O, En P, En Q, En R, B(0, 0) = 0. B(0, 20) = 1400 B(30, 10) = 2200. Es la solución buscada. B(40, 0) = 2000. El beneficio máximo se obtiene produciendo 30 rollos de A y 10 de B. b) Se gastan todas las unidades de algodón y de poliéster. Hay un excedente de 35 − 10 = 25 unidades de seda. c) En este caso se añade una restricción más: x ≥ 15. La región factible cambia (como se puede observar en la figura siguiente) pero la solución óptima no varía. www.profes.net es un servicio gratuito de Ediciones SM ZARAGOZA / SEPTIEMBRE 02. LOGSE / MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES / ÁLGEBRA / OPCIÓN A / EJERCICIO 1 Los nuevos vértices son: O´ = (15, 0), P´= (15, 15), Q y R. El beneficio mayor sigue dándose en Q = (30, 10). www.profes.net es un servicio gratuito de Ediciones SM