Curso de Procesamiento Digital de Imágenes

Curso de
Procesamiento Digital de Imágenes
Impartido por: Elena Martínez
Departamento de Ciencias de la Computación
IIMAS, UNAM, cubículo 408
http://turing.iimas.unam.mx/~elena/Teaching/PDI-Mast.html
elena.martinez@iimas.unam.mx
Programa del Curso
1.
2.
3.
4.
Introducción.
Fundamentos de la imagen digital.
Realce de la imagen en el dominio espacial.
Realce de la imagen en el dominio de la
frecuencia.
5. Restauración de la imagen.
6. Representación del color.
7. Compresión de imágenes.
3. Relace de la imagen en el
dominio espacial
a) Antecedentes.
b) Algunas transformaciones básicas de niveles
de gris.
c) Procesamiento del histograma.
d) Realce de la imagen utilizando operaciones
artméticas/lógicas.
e) Filtros espaciales básicos.
f) Filtros espaciales de suavizamiento (smooth).
g) Filtros espaciales de realce (sharp).
Procesamiento del Histograma
 El histograma de una imagen digital con valores de gris
dentro del rango [0, L-1] es una función discreta h(rk)=nk,
donde rk es el k-ésimo nivel de gris y nk es el número de
pixeles de la imagen que tienen el nivel de gris rk.
 Es práctica común normalizar el histograma dividiendo
cada uno de sus valores por el número total de pixeles en la
imagen, denotado como n, como sigue: p(rk)=nk/n .
 En términos generales, p(rk) es un estimado de la
probabilidad de ocurrencias del nivel de gris rk. La suma de
todos los componentes de un histograma normalizado es = 1
Procesamiento del Histograma
 El histograma es la base de numerosas técnicas de
procesamiento de la imagen en el dominio espacial. La
manipulación del histograma puede utilizarse eficazmente
para el realce de la imagen, como se mostrará aquí.
 Además, veremos más adelante que la información
inherente en el histograma también puede ser utilizada en
otras aplicaciones útiles como compresión de imágenes y
segmentación. Los histogramas son muy fáciles de calcular
por lo que es una herramienta candidata a ser calculada en
tiempo-real.
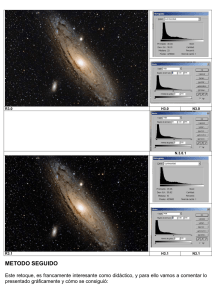
Procesamiento del Histograma
Imagen de granos de polen 700x
Al lado derecho de cada imagen
se muestra su histograma. El eje
horizontal corresponde a los
valores de niveles de gris rk. El
eje vertical corresponde a los
valores de h(rk)=nk o bien,
p(rk)=nk/n si los valores están
normalizados.
Procesamiento del Histograma
 Las imágenes cuyos pixeles tienden a ocupar el rango
dinámico entero de posibles valores de niveles de gris, y
además, tienden a estar distribuídos de manera uniforme,
tendrán una apariencia de mejor contraste y exhibirán una
gran variedad de tonos de gris.
 Es posible desarrollar una función de transformación que
pueda automáticamente realizar este efecto, basado sólo en
la información disponible en el histograma de la imagen de
entrada. Para lo anterior existen 3 tipos de procesos:
Ecualización, Especificación y Realce local.
Ecualización del Histograma
 Supongamos una función continua, y sea la variable r la
que representa los niveles de gris en la imagen a ser
realzada. r está normalizada en el intervalo [0,1] , con r=0
representando el negro y r=1 representando el blanco. Más
tarde consideraremos el caso discreto donde los valores de
los pixeles toman valores en el intervalo de [0,L-1].
 Para cualquier r que satisface lo anterior, definimos la
transformación: s=T(r) , 0  r  1, que produce un nivel s
para cada pixel de valor r de la imagen original.
Ecualización del Histograma
 La transformación s=T(r) , cumple con las siguientes
condiciones:
(a) T(r) es de valor único y monotónicamente
creciente en el intrevalo 0  r  1; y
(b) 0  T(r)  1 para 0  r  1.
 La condición de valor único garantiza que la
transformación inversa exista y el que sea monotónicamente
creciente preserva el orden de los valores de salida de negro
a blanco. La condición (b) garantiza que los niveles de gris
de la imagen de salida estarán en el mismo rango que los de
la imagen de entrada.
Ecualización del Histograma
 La siguiente figura muestra un ejemplo de transformación
que cumple con las dos condiciones mencionadas
anteriormente:
Ecualización del Histograma
 Los niveles de gris de una imagen pueden ser vistos como una
variable aleatoria en el intervalo de [0,1]. Uno de los
descriptores fundamentales de las variables aleatorias es la
función de densidad de probabilidades (PDF).
 Una función de transformación de varibles aleatorias de
particular importancia en el procesamiento de imágenes es la
función de distribución acumulada (CDF). Como las PDF son
siempre positivas, y recordando que la integral de la función es el
area bajo la curva, esta función de transformación es de valor
único y monotónicamente creciente, además que mantienen el
rango de [0,1]. Satisface las condiciones (a) y (b).
Ecualización del Histograma
 Para valores discretos trabajamos con probabilidades y
sumatorias en lugar de funciones de densidad de
probabilidad e integrales. La probabilidad de la ocurrencia
de un nivel de gris rk en una imagen se aproxima como:
nk
pr (rk ) 
n
k  0, 1, 2, ..., L  1
donde n es el número total de pixeles de la imagen, nk es el
número de pixeles que tienen el nivel de gris rk, y L es el
número total de posibles niveles de gris en la imagen.
Ecualización del Histograma
 La versión discreta de la función de transformación (es
decir, de la función de distribución acumulada) es:
k
sk  T (rk )   pr (rj )
k
sk  
nj
j 0
k  0, 1, 2, ..., L  1
n
La imagen procesada (salida) se obtiene mapeando cada pixel
con valor rk de la imagen de entrada a su correspondiente nivel
sk en la imagen de salida. A esta transformación se le llama
ecualización del histograma o linearización del histograma.
La cual satisface las condicionas (a) y (b).
j 0
Ecualización del Histograma
 El resultado de la ecualización del histograma es similar
a la expansión del contraste pero ofrece la ventaja de ser
totalmente automático sin necesidad de dar ningún
parámetro adicional, ya que la ecualización del histograma
automáticamente determina una función de transformación
para producir una nueva imagen con un histograma siempre
uniforme (en la práctica cercano a ser uniforme), ps(s)
(imagen de salida), independientemente de la forma de pr(r)
(imagen de entrada).
Ecualización
del Histograma
La mejora se ve claramente en
las 3 primeras imágenes. La
cuarta no sufre casi cambios
debido a que su histograma
original ya estaba extendido a lo
largo del rango dinámico. Estos
ejemplos muestran el poder de la
ecualización de histograma como
una herramienta de realce
adaptativa.
Especificación del Histograma
 La ecualización del histograma determina
automáticamente la función de transformación y busca
producir una imagen de salida que tenga un histograma
uniforme. El método es simple de implementar.
 Sin embargo, existen aplicaciones en las que intentar
producir histogramas uniformes no siempre es la mejor
opción. En particular, es útil algunas veces tratar de
especificar la forma del histograma de la imagen de salida, a
esta técnica se le conoce como especificación del
histograma (histogram matching).
Especificación del Histograma
 Suponga los niveles de gris continuos r y z (variables
aleatorias continuas), y sea pr(r)y pz(z) sus correspondientes
funciones de densidad de probabilidad. r y z denotan los
niveles de gris de la imagen de entrada y de salida
respectivamente.
 Se puede estimar pr(r) de la imagen de entrada, y pz(z) es
la función de densidad de probabilidad especificada que
deseamos que tenga la imagen de salida.
Especificación del Histograma
PROCEDIMIENTO:
(1) Sea s una variable aleatoria discreta que define una
transformación:
k
sk  T (rk )   pr (rj )
k
nj
j 0
n
sk  
j 0
k  0, 1, 2, ..., L  1
donde n es el número total de pixeles de la imagen, nj es el
número de pixeles que tienen el nivel de gris rj, y L es el
número total de posibles niveles de gris en la imagen.
Reconocemos esta ecuación como la ecualización del
histograma.
Especificación del Histograma
PROCEDIMIENTO:
(2) Del histograma especificado pz(zi), i=0, 1, 2, …, L-1 se
obtiene la función de transformación G(z):
k
vk  G ( z k )   p z ( z i )  s k
k  0, 1, 2, ..., L  1
i 0
Estamos buscando valores de z que satisfagan esta ecuación.
De las dos últimas expresiones sigue que G(z)=T(r). La
variable vk se añadió por claridad con la discusión que sigue.
Especificación del Histograma
PROCEDIMIENTO:
(3) Obtener la función de transformación inversa G-1:
z k  G -1[T(r k )] k  0, 1, 2, ..., L  1
z k  G -1 (s k ) k  0, 1, 2, ..., L  1
Estas dos últimas ecuaciones son el fundamento de la
especificación del histograma.
Especificación del Histograma
 La ecuación del paso (1) es el mapeo de los niveles de gris
de la imagen original a los correspondientes niveles sk
basados en el histograma de la imagen original. La ecuación
del paso (2) calcula la función de transformación G del
histograma especificado pz(z) dado. Y finalmente, las
ecuaciones del paso (3) nos dan una aproximación de los
niveles deseados de la imagen con ese histograma.
 Los dos primeros pasos pueden ser calculados fácilmente
debido a que son datos conocidos, el tercero requiere
explicación adicional.
Especificación del Histograma
NOTAS PARA IMPLEMENTACION:
(1) Cada conjunto de niveles de gris {rj}, {sj} y {zj}, j=1, 2,
…, L-1, es un arreglo unidimensional de L x 1.
(2) Todos los mapeos de r a s y de s a z son simples tablas
lookup entre un valor de pixel dado y estos arreglos.
(3) Para cada uno de los elementos del arreglo, por ejemplo
sk, el subíndice k denota la localización del elemento
dentro del arreglo, y s denota el valor en esa localidad.
(4) Trabajaremos sólo con valores enteros. Esto implica que
los valores de los niveles de gris están en el intervalo [0,
L-1] en lugar de los valores normalizados de [0,1].
Especificación del Histograma
A. s=T(r) de
una imagen.
B. Función de
transformación
hipotética G(z)
C. vk=sk, para
cada z:
G(zk)=sk, o
(G(zk)-sk)=0
Especificación del Histograma
 Como no tenemos las z (encontrarlas es justamente el
objetivo de la especificación del histograma) , debemos
realizar un esquema iterativo para encontrar z de s.
 Para encontrar un valor de zk correspondiente a sk,
debemos iterar para valores de z que cumplan con la
ecuación G(zk)-sk=0, para k=1, 2, …, L-1. No tenemos que
encontrar la inversa de G porque vamos a iterar en z. Como
estamos trabajando con enteros, empezamos con el valor más
pequeño del intervalo zk= ẑ para cada k de manera que:
(G ( zˆ) - s k )  0 k  0, 1, 2, ..., L  1
Especificación del Histograma
RESUMEN PARA IMPLEMENTACION:
(1) Obtener el histograma de la imagen dada.
(2) Ecualizar el histograma para encontrar el mapeo del
nivel rk al nivel sk.
(3) Obtener la función de transformación G del histograma
dado pz(z).
(4) Precalcular zk para cada valor de sk utilizando el
esquema iterativo descrito.
(5) Para cada pixel de la imagen original, si el valor de un
pixel es rk, mapear ese valor a su correspondiente nivel
sk; y luego mapear el nivel sk al nivel final zk. Utilizar los
pasos (2) y (4) para estos mapeos.
Especificación del Histograma
Imagen de la luna de Marte: Fobos tomada por la NASA.
Especificación del Histograma
A. s=T(r) de la
imagen (EH).
B. Imagen
ecualizada
(deslavada).
C. Histograma
de la imagen en
B.
Especificación del Histograma
 El problema de la función de transformación (EH) de la
imagen anterior es causado por la gran concentración de
pixeles en niveles de gris cercanos a 0.
 Una manera de resolverlo sería modificando el histograma
de la imagen de manera que no tenga esta propiedad. Se
necesita una función especificada manualmente que preserve
la forma general del histograma pero que tenga una
transición más suave de niveles en regiones oscuras de
niveles de gris.
Especificación
del
Histograma
Curva 1: función
G(z) obtenida del
histograma
especificado.
Curva 2: función
inversa G-1(s)
obtenida por el
método iterativo.
Especificación del Histograma
 La especificación del histograma es una tarea que se realiza a
ensayo y error. Se pueden utilizar guías aprendidas del problema
en cuestión como el que se presentó anteriormente.
 Podrían haber casos en que sea posible formular un especie de
histograma “promedio” de cómo debería ser el histograma de
una imagen, y utilizar éste como la especificación. En ese caso la
especificación del histograma resulta en un proceso sencillo.
 Sin embargo, en general no existen reglas para especificar
histogramas y uno debe basarse en el análisis de caso por caso.
Realce Local
 Los métodos de procesamiento del histograma discutidos
anteriormente son globales, en el sentido de que los pixeles
se modifican por funciones de transformación basadas en el
contenido de niveles de gris de la imagen entera. Aunque el
realce global es adecuado para una mejora general, existen
casos en los que es necesario realzar detalles sobre areas
pequeñas de una imagen.
 Las técnicas vistas anteriormente son fácilmente adaptables
para hacer realce local.
Realce Local
 El procedimiento consiste en definir una vecindad
cuadrada o rectangular y mover el centro de esta área pixel
por pixel. En cada posición, se calcula el histograma del área
en cuestión y se realiza la ecualización o la especificación
del histograma del vecindario. Esta función de mapeo
finalmente se aplica sólo al pixel central del vecindario. El
pixel central se mueve a la siguiente posición y el esquema
se repite.
Realce Local
(a) Imagen original que ha sido ligeramente suavizada para
reducir el ruido (veremos el suavizamiento después).
(b) Ecualización global del histograma.
(c) Ecualización local de vecindarios de tamaño 7 x 7.
Instituto de Investigaciones en
Matemáticas Aplicadas y en Sistemas
(IIMAS)
http://turing.iimas.unam.mx/~elena/Teaching/PDI-Mast.html