El pórtico ABCD de la figura es de sección rectangular de 30
Anuncio

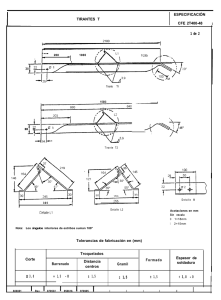
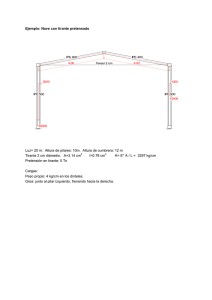
El pórtico ABCD de la figura es de sección rectangular de 30 cm de ancho y 60 cm de canto, y el módulo de elasticidad del material del que está fabricado es 20 GPa. Entre las secciones A y D hay un tirante de acero de 2 cm2 de sección y 210 GPa de módulo de elasticidad, cuya longitud puede variar por medio de un manguito roscado. En el dintel del pórtico actúa una sobrecarga uniforme de 15 kN/m. Antes de aplicar la sobrecarga, y por medio del manguito roscado, se acorta la longitud AD del tirante lo preciso para que, al aplicar la sobrecarga, la distancia AD vuelva a ser 16 m. Determinar el valor de la tensión en el tirante y de las máximas tensiones de tracción y compresión en la sección H (sección media del dintel). q B C H 8m A D 6m 4m 6m q B C 8m A F F 6m 4m D 6m El desplazamiento horizontal de D, al aplicar la sobrecarga, debe ser nulo. q B C = A F F D q B C B C + A D ESTADO 1 A F F ESTADO 2 D Estado 1: q B A C D 4q/2 4q/2 Calcularemos el desplazamiento horizontal de D considerando: a) la reacción vertical en D b) la sobrecarga en el dintel Estado 1(a): (4q/2)10 (4q/2)10 (4q/2)6 (4q/2)16 (4q/2)6 B A C D 4q/2 4q 4q ⎡ ⎤ + 10 6 ⎢ ⎥ 1 1 4q 2 1 4q 1 4q r 2 2 ⋅ ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ u D ( reacción en D ) = 8 10 6 8 10 10 4 10 6 8 4 ⎢ ⎥= EI ⎢ 2 2 2 2 3 2 2 3 ⎥ ⎣ ⎦ 1792q = EI Estado 1(b): 8q 4q.2=8q q C B 32q A D r 1 ⎡1 1 1 ⎤ u D ( sobrecarga ) = − ⎢ 4 ⋅ 8q ⋅ 8 + 10 ⋅ 24q ⋅ 8 + 10 ⋅ 8q ⋅ 4⎥ = EI ⎣ 3 2 3 ⎦ 725 ,33q =− EI Estado 2: 8F 8F 8F 8F C B F F r u D ( fuerza =− 682 ,66 F EI F )=− 1 EI D ⎡ ⎛1 ⎤ 2 ⎞ 2 + ⋅ ⋅ = ⋅ ⋅ 10 8 F 8 4 8 F 8 ⎜ ⎟ ⎢ 2 ⎥ 3 ⎠ ⎣ ⎝ ⎦ r 1792q 725 ,33q 682 ,66 F uD = − − = 0 ⇒ F = 23 ,4375 kN EI EI EI Tensión en el tirante: 23437 ,5 σ= = 117 ,19 MPa −4 2 ⋅ 10 Tensiones en la sección H: Esfuerzo axil (compresión): 23,4375 kN Momento flector: (4q/2)8-2q-F.8=22,5 kN.m σcompresión = H σ traccíón H 23437 ,5 22500 ⋅ 0 ,3 + = 1,38 MPa 0 ,3 ⋅ 0 ,6 1 0 ,3 ⋅ 0 ,63 12 23437 ,5 22500 ⋅ 0 ,3 =− + = 1,12 MPa 1 0 ,3 ⋅ 0 ,6 0 ,3 ⋅ 0 ,63 12