1 IntroducciQn
Anuncio
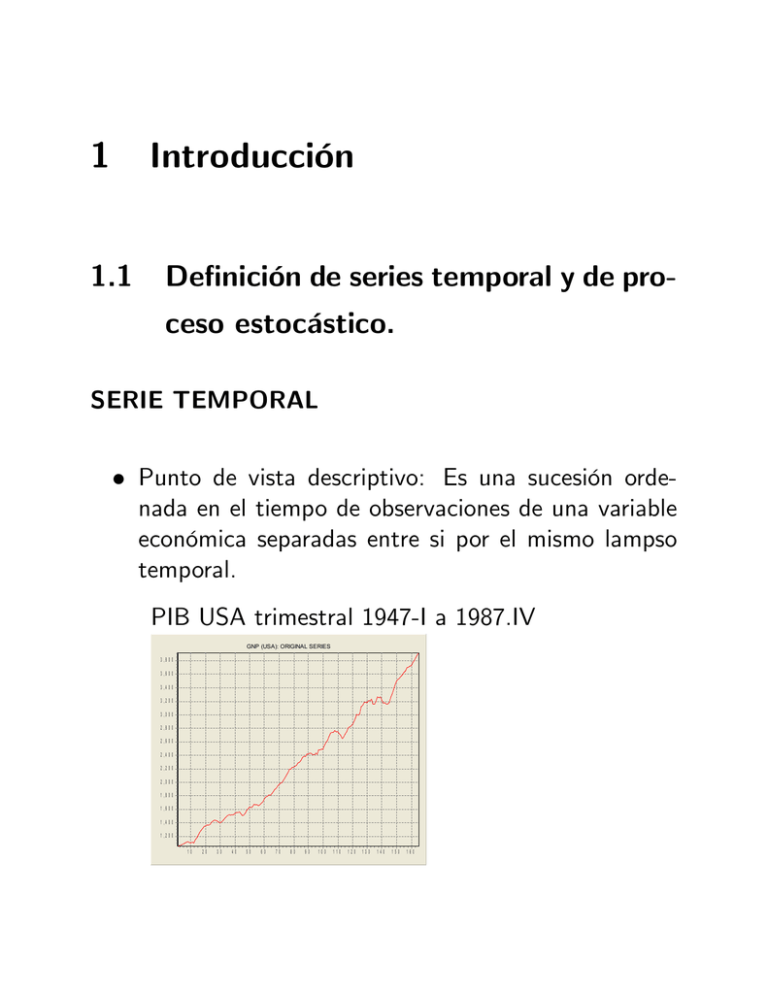
1 1.1 Introducción De…nición de series temporal y de proceso estocástico. SERIE TEMPORAL Punto de vista descriptivo: Es una sucesión ordenada en el tiempo de observaciones de una variable económica separadas entre si por el mismo lampso temporal. PIB USA trimestral 1947-I a 1987.IV GNP (USA): ORIGINAL SERIES 3,800 3,600 3,400 3,200 3,000 2,800 2,600 2,400 2,200 2,000 1,800 1,600 1,400 1,200 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 Las series la podemos clasi…car por tanto desde este punto de vista en cuanto a su periodicidad en anuales, trimestrales, mensuales, ... Existen básicamente dos enfoques para el tratamiento de series temporales el enfoque determinta y el enfoque estocástico. En primer lugar describiremos brevemente el enfoque determinista y con posterioridad nos centraremos en el enfoque estocástico. 1.2 Enfoque determinita de series temporales. En esta aproximación se suele suponer que la serie analizada puede ser expresada como la agregación de sus componentes no observables. Los economistas tienden a clasi…car los movimientos o oscilaciones de las series económicas diferenciando entre componentes tendencial, ciclíco, estacional e irregular. Se les conoce como componentes no observables, dado que se man…estan de forma conjunta en la serie temporal, pero no son observables por separado. Tradicionalmente los economistas han considerado como componentes de interés la tendencia y el cíclico. Y los componentes estacional e irregular como provocados por factores exógenos e independientes a los factores económicos. Tendencia y tendencia ciclo: El comportamiento tendencial de las series temporales está asociado a oscilaciones con período de repetición superior a 5 años. Por lo que respecta a al componente cíclico se identi…ca con aquellas oscilaciones asociadas a períodos de repeticción compredidos entre 5 años y un año. El límite entre componente tendencial y cíclico es arbitrario, por lo que en la práctica se suele hablar de componente tedencia-ciclo, que se identi…ca con oscilaciones que se repiten con un período de repetición compredidio entre in…nito y un año. Es decir, el componente ciclo-tendencia se identi…ca con las oscilaciones de medio y largo plazo. Componente estacional: Se identi…ca con las oscilaciones de caracter períodico o cuasi-periodico de duración anual o inferior a la anual. Componente irregular: Se identi…ca a oscilaciones no asociadas a los componentes tendencia-ciclo y estacional. En este enfoque se asume que la serie temporal es el resultado de combinar todo los componentes no observables: Adtivo Multiplicativo xt = Tt + St + It: xt = Tt St It: El metodo más extendido en este enfoque son los alisados exponenciales. Existen varios métodos dependiendo de si la serie temporal presenta tendencia y estacionalidad. El método más completo es de Holt-Winters que permite obtener predicciones de series temporales que presenten estacionalidad. 1.3 Enfoque estocástico. Punto de vista estocástico: Una serie temporal es la realización de un proceso estocástico. Proceso estocástico: Un proceso estocástico es un conjunto ordenado de variables aleatorias que depende de un indicador. En el caso de lasn series temporales el indicador es el tiempo t fxtg ; xt1 ; xt2 ; xt3 ; :::; xtn g. Tambíén se puede decir que un proceso estocástico es una sucesión de v.a. ordenadas en el tiempo (sólo válido para ST). Por tanto, una serie temporal es una muestra T -dimensional de tamaño 1, o lo que es lo mimo, una serie temporal es una realización de tamaño muestral 1 de cada una de las variables aleatorias que integran el proceso estocástico. Como sólo vamos a disponer de una única realización muestral por v.a., será necesario asumir que se cumplirán un conjunto de supuestos para poder trabajar con las series temporales para poder extraer conclusiones a partir de la información de la series temporal (muestra) que sean válidas para el proceso estocástico (población). Estos supuestos o propiedades serán básicamente la estacionariedad y la ergodicidad. 1.4 Ergodicidad y estacionariedad. Dado que un proceso estocástico es un conjunto de variables aleatorias y que las v.a. se caracterizan através de sus funciones de distribución y densidad y de sus momentos poblacionales (valor esperado, varianza, covarianzas, ...), caracterizemos los procesos estocásticos através de la Función de Distribución Conjunta del proceso estocástico y de los momentos poblacionales: F xt1 ; xt2 ; xt3 ; :::; xtn h i h i E xt1 ; E xt2 ; :::; E [xtn ] h i h i V AR xt1 ; V AR xt2 ; :::; V AR [xtn ] h i h i COV xt1 xt2 ; COV xt1 xt3 ; ::: Por ejemplo, supongamos que estamos analizando la serie temporal del PIB USA del grá…co anterior, como disponemos de 165 observaciones para caracterizar el proceso estocástico deberíamos sacar conclusiones sobre las v.a.’s integrantes del proceso estocástico a partir de realizaciones muestrales de tamaño 1. Es decir, por ejemplo a partir de una única observación obtener conclusiones sobre el valor esperado E [ ] y varianza V AR [ ]de una variable aleatoria. Estacionariedad en sentido estricto: Un proceso estocástico se dice que es estacionario en sentido estricto o fuerte si para un subconjunto ft1; t2; ::; thg se cumple: F xt1 ; xt2 ; :::; xth = F xt1+k ; xt2+k ; :::; xth+k : Es decir, que la función de distribución conjunta es invariante ante deplazamientos en el tiempo. Por lo tanto, también será invariante ante desplazamientos en el tiempo todos los momentos poblacionales, dado que estos se de…nen a partir de la función de densidad. Esta propiedad es muy difícil de comprobar o casi imposible. Estacionariedad en sentido débil: Se dice que un proceso estocástico es estacionario en sentido débil o de segundo orden, cuando se cumplen simultáneamente las tres siguientes condiciones: E [x t ] = E x t k = V AR [xt] = V AR xt k = 2 h i h i COV xt1 ; xt2 = COV: xt1 k ; xt2 k 8k = 1; 2; :: La estacionariedad en sentido estricto implica estacionariedad en sentido débil, pero la existencia de estacionariedad en sentido débil sólo implica estacionariedad en sentido estricto cuando el proceso estocástico sigue una ley normal. En la práctica se trabaja con el concepto de estacionariedad en sentido débil que implica que el valor esperado y la varianza son constantes y que la covarianza entre v.a.’s asociadas a distintas observaciones sólo depende del lapso temporal que las separa. Ergodicidad: La condición su…ciente (pero no necesaria) de ergodicidad para un proceso estacionario consiste en que se cumpla: 0 1 lim @ T !1 T T X k=1 1 COV xt; xt k A = 0: La ergodicidad permite limitar el grado de dependencia temporal y nos permite modelizar la dependencia temporal de un proceso estocástico utilizando un conjunto …nito de parámetros. Se introduce para eliminar la dependencia de xt de valores pasados muy lejanos. La ergodicidad es un supuesto que no es contrastable a partir de una sola realización del proceso estocástico, por lo tanto, es una hipótesis que se asume pero no se contrasta. 1.5 Funciones de autocovarianzas, autocorrelación simple y parcial. Para caracterizar los procesos estocásticos estacionarios ergódicos utilizaremos las funciones de autocorrelación, que nos permiten medir la asociación entre las variables aleatorias de un proceso estocástico separadas entre si por un lapso temporal. A la covarianza entre dos variables aleatorias integrantes de un mismo proceso estocástico la llamaremos autovarianza k y dado que asumiremos que los procesos son estacionarios k se re…ere al lapso temporal que separa a las dos observaciones: k donde = COV xt; xt k = E (xt E [xt]) xt k = E ( xt ) xt k E xt k : E [x t ] = E x t k = : Para los procesos estacionarios se cumplen las siguientes propiedades: 2>0 = V AR [ x ] = t 0 k = k 1: k+i k 8i Al conjunto de todas las autocovarianzas que se pueden calcular para una serie temporal o proceso estocástico se le llama función de autocovarianzas 0; 1; 2 ; :::; k ; k+1 ; ::. A partir de la autocovarianza de order k ( k ) se de…ne la autocorrelación de order k ( k )como: k = : k 0 Y es fácil ver que se cumple: = 1 k = k 1: k+i k 8i 1 1 k 0 (1) Al conjunto de todas las autocorrelaciones que se pueden calcular se le llama función de autocorrelación simple (FAS) 1; 2; :::; k ; k+1; ::. también es de utilidad de…nir los coe…cientes de autocorrelación parcial como: k;k h i = Corr xt; xt k jxt 1; :::; xt (k 1) : Es decir, estos coe…cientes, a diferencia de los coe…cientes de correlación simple k que miden la correlación entre dos v.a.’s separadas entre si por k períodos, miden las correlacion entre xt y xt k pero descontando el efecto de xt 1; :::; xt (k 1). Una forma sencilla de entender la idea es através de la siguiente regresión: xt = xt 1 k;1 + xt 2 k;2 + ::: + xt k k;k + ut El parametro que medirá el efecto que tiene una variación de xt k sobre xt, descontando el efecto de las observaciones intermedias es k;k . Si multiplicamos la expresión anterior por xt j y tomamos esperanzas (asumiendo que E [xt] = 0) es fácil ver que: xt j xt = xt j xt 1 k;1 + ::: + xt j xt k k;k +xht j ut i i h i h E xt j xt = E xt j xt 1 k;1 + ::: + E xt j xt k k;k h i + E xt j u t j = j 1 k;1 + j 2 k;2 + ::: + k j k;k j = j 1 k;1 + j 2 k;2 + ::: + k j k;k ; asumiendo que E xt k ut = 0. Por lo tanto, existe una relación entre los coe…cientes de autocorrelación simple j y parcial j;j . Dando valores a j obtenemos el sistema: = 2 = 1 k = + 1 k;2 + ::: + k 1 k;k 1 k;1 + k;2 + ::: + k 2 k;k k;1 ... k 1 k;1 + k 2 k;2 + ::: + k;k Que permite obtener la siguiente relación: 1;1 = 1 1 k;k = ::: k 1 1 ::: k 2 1 1 ::: k 3 2 1 ... ... ... ... ... 1 k 1 k 2 k 3 ::: : (2) 1 ::: 1 1 2 1 ::: 2 1 1 1 ::: 3 2 1 ... ... ... . . . ... k 1 k 2 k 3 ::: k 1 2 1 Al conjunto de todos los coe…cientes de autocorrelación parcial se le llama función de autocorrelación parcial (FAP). Tal y como iremos viendo las funciones autocorrelación simple y parcial se representan grá…camente, lo que recibe el nombre de correlograma. Nosotros identi…caremos el tipo de proceso estocástico que sigue una serie en base a analizar el correlograma de dicha serie. Pero utilizaremos los correlogramas muestrales que son fáciles de obtener una vez que estimamos las autocovarianzas muestrales utilizando: ^k = 1 X T k 1X ^0 = ( xt T 1X x = xt ; T ( xt x) xt k x x) 2 entonces es inmediato obtener los coe…cientes de la FAS y la FAP utilizando (1) y (2), pero sustituyendo j por ^ j y j por ^j . 1.6 Procesos de Ruido Blanco y Paseo Aleatorio. Se dice que una serie sigue un proceso de ruido blanco cuando responde al siguiente esquema: xt = "t "t iid 0; 2" donde iid 0; 2" signi…ca idénticamente e independientemente distribuidos con valor esperado 0 y varianza 2" . Es fácil ver que para un ruido blanco se cumple: E [xt] = E ["t] = 0 2 = V AR [ x ] = V AR [ " ] = t t 0 " k = COV xtxt k = COV "t"t k = 0 k =0 k = 0 8k 1: Por lo tanto presenta un correlograma con todos los coe…entes iguales a cero. Este proceso es el proceso estacionario más sencillo de todos y, a partir del cual de…niremos en resto de procesos que analizaremos. Se dice que una serie sigue un proceso de paseo aleatorio cuando responde al siguiente esquema: xt = xt 1 + "t "t iid 0; 2" : (3) Tal y como veremos a continuación es el proceso no estacionario más sencillo que se puede de…nir. Si sustituimos recursivamente en (3) es fácil ver que: xt = xt 1 + "t = (xt 2 + "t 1) + "t = (xt 3 + "t 2) + "t 1 + "t ... xt = x0 + t X "t i=1 Donde x0 es una observación inicial, entonces tenemos: 2 E [xt] = E 4x0 + t X i=1 3 "t5 = x0 + E ["1 + "2 + + "t] = x0 + E ["1] + E ["2] + + E ["t] = x0 + 0 + 0 + Y en cuanto a la varianza: + 0 = x0 : 2 V AR [xt] = V AR 4x0 + t X i=1 3 "t5 = V AR ["1 + "2 + + "t] = V AR ["1] + V AR ["2] + = 2 " + 2" + + V AR ["t] + 2" = t 2" : Por lo tanto no es estacionario, dado que, la varianza depende del período temporal en el que nos encontramos. Si añadimos una deriva , pasariamos a tener: xt = + xt 1 + "t "t iid 0; 2" : Si sustituimos recursivamente: xt = + xt 1 + "t = + ( + xt 2 + "t 1) + "t = 2 + ( + xt 3 + "t 2) + "t 1 + "t ... xt = x0 + t + t X "t i=1 entonces tenemos: 2 E [xt] = E 4x0 + t + t X i=1 3 "t5 = x0 + t Y en cuanto a la varianza: 2 V AR [xt] = V AR 4x0 + t + = t 2" : t X i=1 3 2 "t5 = V AR 4 t X i=1 3 "t5 En este caso, tanto el valor esperado como la varianza depende del período temporal en el que nos encontramos.