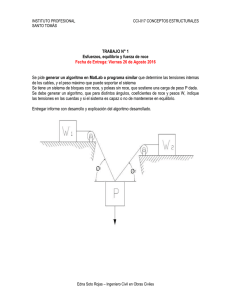
1 a) Medir los coeficientes de roce: estático μe y, dinámico μd, para

3
1.- OBJETIVOS
a) Medir los coeficientes de roce: estático e y, dinámico d, para varias superficies en
contacto.
b) Verificar que los coeficientes de roce solo dependen del tipo de superficies en contacto
c) Comprobar que para un mismo par de superficies en contacto; d  e
2.- MATERIALES





Plano con inclinación variable y transportador con plomada
Regla graduada y cinta métrica
Polea con contrapeso
Bloques de madera de diferentes tamaños
Hojas de papel bond, cinta adhesiva y tijeras
3.- TEORÍA
Si para deslizar un cuerpo pesado sobre una alfombra se aplica una fuerza pequeña, el
cuerpo no se moverá, esto se debe a que, con esa fuerza no se puede vencer la resistencia
que opone la fuerza de fricción. Si se aumenta lo suficiente la fuerza aplicada el cuerpo
comienza a deslizar, y, a partir de ese momento se necesita aplicar una fuerza menor
para mantenerlo en movimiento. Una vez que se detiene es necesaria una fuerza
mayor para ponerlo en movimiento otra vez. Naturalmente, todo esto es más fácil si el
cuerpo es liviano y la fuerza de contacto entre él y la superficie donde se encuentra es
pequeña. También sería más sencillo moverlo sobre un piso de cerámica que sobre la
alfombra.
1
Este ejemplo ayuda a recordar varias propiedades importantes de la fricción:
 La fricción actúa en forma distinta entre superficies estacionarias (fricción
estática o adherencia), que entre superficies deslizantes (fricción cinética).
 Hasta cierto límite superior, la fricción estática entre las superficies tiene la
magnitud necesaria para evitar que esas superficies deslicen entre sí.
 El límite superior de la fricción estática aumenta a medida que la fuerza
perpendicular a las superficies en contacto aumenta, o sea, la fuerza que une las
superficies en contacto de los cuerpos.
 La fricción cinética también aumenta con la magnitud de la fuerza normal entre
las superficies deslizantes, pero, no tiene un rango de valores por debajo de un
límite superior, sino; un único valor.
Experimentalmente se ha demostrado que en la mayoría de los casos el valor máximo
de la fuerza de roce estático está dado con muy buena aproximación, por:
fmax = sN
(1)
donde s, es una constante que depende únicamente del tipo de superficies en contacto, y
N, la fuerza normal entre ellas. La fuerza de roce estático, de tal manera, satisface la
relación:
fs  sN
(2)
También se encuentra que para una amplia gama de aplicaciones la fuerza de roce
cinético, está dada por una relación similar:
fk = kN
(3)
Donde k, es el coeficiente de roce cinético, el cual, al igual que s, depende
únicamente de las superficies en contacto. Para todos los materiales se ha encontrado que:
k  s
(4)
Las ecuaciones (1), (2) y (3), son leyes empíricas que describen el comportamiento de
las fuerzas de fricción en muchas condiciones. Aunque estas formulas son muy útiles para
muchos propósitos prácticos, no tienen el status de estamentos matemáticos que representen
principios físicos generales. De hecho hay casos en los cuales no son una buena
aproximación. Por ejemplo en superficies lubricadas o, cuando las superficies deslizan a
altas velocidades.
MEDIDA DEL COEFICIENTE DE ROCE ESTÁTICO:
s
Para medir el coeficiente de roce estático s se usará un método sencillo, pero, algo
delicado. Se coloca un bloque sobre una superficie rugosa la cual está adosada a un plano
2
de inclinación variable (Figura 1). Una vez colocado el bloque sobre el plano, se aumenta
lentamente el ángulo  hasta que el bloque comience a deslizar. Este ángulo crítico c, para
el cual se rompe el equilibrio entre la fuerza de roce y la componente del peso en dirección
del plano, cumple con la relación:
 S  tng C
(5)
Así; si se mide este ángulo c se puede determinar el coeficiente de roce estático
Fig. 1
MEDIDA DEL COEFICIENTE DE ROCE CINÉTICO:
k
Fig. 2
Para medir el coeficiente de roce cinético k se hará uso del teorema del trabajo y la
energía. La figura 2 muestra dos cuerpos de masas MA y MB, vinculados por medio de una
cuerda de masa despreciable, que pasa por una polea de masa mp.
3
El sistema se coloca inicialmente en reposo con los cuerpos A y B en los puntos
denotados con “1”, de modo que B se encuentra a una altura H del suelo. Al dejar caer el
cuerpo B, las masas se aceleran desde la posición “1” hasta la posición “2”, donde el cuerpo
B se detiene. El desplazamiento de ambas masas en esta primera etapa del movimiento es
igual a H y, un instante antes de detenerse el cuerpo B, ambas tienen velocidad V.
Aplicando el teorema del Trabajo y la Energía, igualamos el trabajo hecho por la
fuerza de roce a la variación de la energía mecánica.
Trabajo(roce) = E cinética + E potencial
1
(6)
M A  M B   V 2  1 I 2  M B gH
2
2
1
Donde el término: I 2 es la energía cinética rotacional de la polea. Al sustituir en
2
1
esta expresión el momento de inercia de la polea: I  m p  R 2 ( m p  masa de la polea y
2
V
1 2 1
R = radio), y la velocidad angular:   Se tiene que:
I = m p  V 2 y la ecuación
4
2
R
(6) adopta la expresión:
1
1
(7)
  k M A gH  M A  M B   V 2  m p  V 2  M B gH
2
4
  k M A gH 
En la segunda etapa del movimiento (ver figura 3), el cuerpo B permanece en reposo,
mientras el A se mueve desde el punto “2” hasta el punto “3”, donde se detiene después de
haber efectuando un desplazamiento adicional “D”.
Fig. 3
Entonces, por el teorema del Trabajo y la Energía se tiene:
1
  k M A gD   M AV 2
2
(8)
4
De las ecuaciones: (7) y (8) se deduce:
k 
MBH
(9)
1


M A H  D  M A  M B   m p 
2


En conclusión, para medir  k es suficiente con medir las masas, mp, MA, MB y las
distancias H y D.
4.- ACTIVIDADES PREVIAS A LA SESIÓN DE PRÁCTICA
Elabora un preinforme con el siguiente contenido:
1.
2.
3.
4.
5.
Define los objetivos específicos de la práctica
Describe brevemente los dispositivos experimentales que usarás
Indica las magnitudes físicas y otras cantidades que medirás directamente
Indica las magnitudes físicas y otras cantidades que medirás indirectamente
Indica cuales son las cantidades de mayor interés en el experimento
5.- PARTE EXPERIMENTAL
El análisis y procesamiento de los datos se hará en el libro de Excel: “ROZAMIENTO”
ACTIVIDAD 1
MEDIDA DEL COEFICIENTE DE ROCE ESTÁTICO:
s
1.- Medida de s para las superficies papel sobre acetato.
1.
Si lo consideras necesario, vuelve a forrar los dos bloques de madera cambiando el
papel bond. La lámina de acetato debes fijarla con chinches sobre la superficie de
corcho del plano inclinado.
2.
Coloca el bloque MA1 forrado con el papel bond, sobre la superficie de acetato del
plano inclinado y, lentamente, aumenta el ángulo de inclinación del plano hasta que el
bloque empiece a deslizar, anota el valor de este ángulo en la tabla indicada de la hoja
de cálculo. Disminuye la inclinación del plano.
3.
Repite diez veces el paso 2.
4.
Para cada ángulo, calcula el valor del coeficiente de roce estático entre las superficies
de papel sobre acetato, ecuación (5) de la parte teórica.
 s( p a) M 1  tng C
5.
Encuentra la desviación estándar de los valores del coeficiente de roce:
 s ( p a ) M 1
5
6. Reporta como valor de
de su error estadístico:
 s ( p a ) M 1
 s ( p a ) M 1 
el promedio de los 10 valores medidos, acompañado
3 s ( p a ) M 1
10
7. Repite este procedimiento (pasos del 2 al 6) usando el otro bloque: MA2, de diferente
masa y área de contacto.
8. Calcula la magnitud de la diferencia entre los dos coeficientes encontrados:
 s ( p a ) M 1   s ( p a ) M 2
9. Analiza (en la hoja de análisis) si de acuerdo con la teoría, estos coeficientes son
iguales dentro de sus respectivos errores, esto es:
a) Si la magnitud de la diferencia entre los dos coeficientes es menor que el menor de
los errores; entonces: los coeficientes son iguales.
b) También: si al sumarle su error al coeficiente menor y restarle su respectivo error al
coeficiente mayor, el orden de tamaño se invierte; los coeficientes son iguales.
2.- Medida de s para las superficies: papel sobre papel.
10. Cubre la superficie del plano inclinado con una cinta de papel bond. Fíjala al corcho
con chinches, y procede a medir el coeficiente de roce estático para las superficies:
papel sobre papel µs(p-p). Como en el caso anterior tienes que hacerlo para los dos
bloques, siguiendo los pasos del 2 al 8, anotando las medidas, cálculos, y análisis, en
los lugares indicados de las hojas de cálculo.
MEDIDA DEL COEFICIENTE DE ROCE CINÉTICO:
k
Se medirá el coeficiente de roce cinético para las superficies: papel sobre papel, por
medio del arreglo que se describe en las de la parte teórica.
11. Forra con papel bond la superficie de la mesa por donde se desplazarán los bloques de
madera identificados como MA en las figuras 2 y 3. Si ya está forrada, pero, lo
consideras necesario, cambia el papel. Seguramente necesitarás colocar más de una
hoja de papel, colócalas de modo que los bloques al deslizar no tropiecen con los
cantos de las hojas.
12. Debes colocar en el piso un tope de cartón donde caerá el bloque MB. Ubícalo en el
lugar apropiado para que el contrapeso no se dañe al golpear con el piso, ni dañe el
piso
6
Los valores de las masas de cada bloque de madera corresponden a la masa “M A” tanto
en las figuras 2 y 3, como en la ecuación (9). La masa del contrapeso corresponde a la masa
“MB”. Los valores de estas masas, así como el valor de la masa de la polea “mp” están
indicados en la hoja de cálculo.
13. Toma el bloque MA1 y únelo al contrapeso por medio de la cuerda. Pasa la cuerda por
la polea que se encuentra en el borde de la mesa, y, desliza el bloque sobre la mesa
hasta que la cuerda se tense sin que el contrapeso se levante del suelo, marca con lápiz
el lugar del borde delantero del bloque, esta es la posición donde la tensión se anula y
el contrapeso deja de acelerar los bloques (corresponde a la posición “2” en las figuras
2 y 3).
14. Desde la posición que marcaste como de “tensión cero”, desliza el bloque hacia atrás
18 cm. en consecuencia, el contrapeso se levantará una altura H de 18 cm. Sin mover
el bloque marca sobre el papel el borde delantero del mismo. Esta será la posición
inicial desde donde soltarás los bloques. Es recomendable que uses una misma altura
H para todas las medidas, por lo tanto, ésta, que marcaste, será la posición inicial para
todos los desplazamientos, tanto de la primera masa coma de la segunda. Anota este
valor de H en la celdas correspondientes de la hoja de cálculo
15. Ahora, procede a tomar las medidas. Vuelve a colocar el bloque MA1 con su borde
delantero en la posición inicial y suéltalo para que deslice sobre la mesa, mide la
distancia entre la posición de “tensión cero” y el punto donde se detiene, esta es la
distancia D de la figura 3 y de la ecuación (9). Anota la medida en el lugar
correspondiente de la hoja de cálculo.
Nota: no sueltes MA1 si el contrapeso está oscilando. Debes detener las oscilaciones
antes de soltarlo.
16.
Repite el paso anterior doce veces.
17.
Calcula para cada distancia D, el coeficiente de roce dinámico µk(M1)
k 
MBH
1


M A H  D  M A  M B   m p 
2


(9)
18. Calcula la desviación estándar σk(M1) de los valores de µk(M1)
19. Reporta como valor de µk(M1) el promedio de los 12 valores medidos, acompañado de
su error estadístico:
 k ( M 1) 
3 k ( M 1)
12
7
20. Repite los pasos del 15 al 19, esta vez con el bloque MA2, para volver a medir el
coeficiente de roce dinámico entre las mismas superficies, pero, con un bloque de masa
y superficie de contacto, diferentes: µk(M2).
21. Calcula la magnitud de la diferencia entre los dos coeficientes encontrados:
 k ( M 1)   k ( M 2)
22. Analiza si de acuerdo con la teoría, estos coeficientes son iguales dentro de sus
respectivos errores, esto es:
c) Si la magnitud de la diferencia entre los dos coeficientes es menor que el menor de
los errores; entonces: los coeficientes son iguales.
d) También: si al sumarle su error al coeficiente menor y restarle su respectivo error al
coeficiente mayor, el orden de tamaño se invierte; los coeficientes son iguales.
ANÁLISIS
1. ¿Los valores obtenidos corroboran que el coeficiente de roce estático entre las
superficies: papel y acetato, es independiente del área de contacto?. Explica claramente.
2. Contesta la pregunta anterior para el coeficiente de roce estático, entre las dos
superficies de papel.
3. ¿Los valores obtenidos corroboran que el coeficiente de roce dinámico entre las dos
superficies de papel, es independiente del área de contacto? Explica claramente
basándote en los valores y sus respectivos errores de  k 1 y  k 2  .
4. ¿Los resultados experimentales, corroboran que el coeficiente de fricción cinética es
menor que el de fricción estática?. Explica claramente.
5. ¿Si tu respuesta a la pregunta anterior no es afirmativa. ¿A qué crees que se debió esta
discrepancia con la teoría?
8