Guia-III - Electrónica Aplicada II
Anuncio

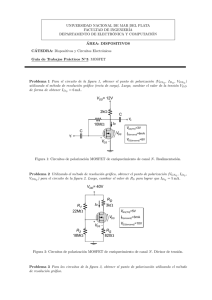
Problema 30 Analizar el amplificador JFET fuente común de una etapa que se muestra en la figura 2. Determinar: AV, Ai, RiA y RoA. IDSS=2mA, Vp=-2V, rds=100K, RG=30K, RD=10K, RL=2,67K, RS1=100Ω, RS2=300Ω Análisis estático: VGS ID = IDSS ⋅ 1 − Vp 2 VGS = − ID ⋅ ( RS1 + RS 2) ID = 1mA Con este primer valor itero VGS=-0,4V ⇒ ID=1,28mA ID=1,2mA ⇒ VGS=0,48V ⇒ ID=1,15mA finalizando la iteración se llega a: ID=1,17mA ⇒ VGS=0,468V hallo VDS: VDS = VDD − ID ⋅ ( RD + RS1 + RS 2) = 7 ,832V supongo VDD=20V Análisis dinámico: rds g Vi gm = − vgs s gm.vgs 2 ⋅ IDSS ID ⋅ = 1,53mS RG Vp IDSS RS1 d RD RL 169 vo Aplicando la expresión de ganancia para RS sin puentear: AV = − gm ⋅ Rd = −2 ,8 1 + gm ⋅ RS1 se supone rds muy grande Rd = RL RD = 2 ,1K Resistencias: Ri ≅ ∞ Ro = ro ⋅ (1 + gm ⋅ RS1) = 115K RiA ≅ RG = 30K RoA = Ro RD = 9200Ω Ros = RoA RL = 2065Ω Problema 31 Diséñese un amplificador JFET que tenga una: RL=10K, VDD=12V, RiA=500K y AV=-2. Utilizar el circuito de la figura 1. Para el punto de trabajo VGSQ=-1V e IDQ=1mA la trasconductancia del transistor tiene un valor de 2,5mS. Análisis de contínua: VDD R1 VGS ID = IDSS ⋅ 1 − Vp RD gm = −2 ⋅ R2 RS IDSS VGS ⋅ 1 − Vp Vp IDSS = 5mA Vp = −1,8V Adopto IDQ=3mA VGSQ = 1 − IDQ ⋅ Vp = −0,405V IDSS 170 2 RG VDSQ = 7V VGG VGS RD + Rs = gm = 2 ⋅ RS se elige haciendo un gráfico a escala de ID=f(VDS) VDD = VDSQ + IDQ ⋅ ( RS + RD) VDD − VDS 12V − 7V = = 1,67 K ID 3mA IDSS VGS ⋅ 1 − = −4,3mS Vp Vp AVs = − gm ⋅ Rd = −2 1 + gm ⋅ RS Itero: RD RL = 464 ,15Ω 1 + gm ⋅ Rs RD + Rs = 1670Ω Adopto: esta ecuación es flexible y puede variar RD=1,8K y Rs=470Ω VGG = VGS + ID ⋅ RS = 1V VGG ⋅ R1 = VDD ⋅ R1 = R2 ⋅ R1 R1 + R 2 VDSQ = 5,2V VDD ⋅ RG = 6 MΩ VGG VDSQ > Vp − VGS 1 1 1 + = R1 R 2 500K R2 = 545K Entonces adopto: R1=6M2 y R2=560K Verifico: RG=513K y AVs=2,17 171 Problema 32 Diséñese un amplificador JFET drenaje común con las siguientes especificaciones: Ai=12, RL=400Ω, VDD=12V. Las características del transistor disponible son: IDSS=20mA y Vp=-7V. Utilizar la configuración de la figura 3. Calcular RoA del circuito resultante. Análisis estático: IDQ = 0,6 ⋅ IDSS = 12 mA VGS ID = IDSS ⋅ 1 − Vp gm = − ⇒ IDQ VGS = − 1 ⋅ (−Vp ) = −1,58V IDSS 2 VDSQ = 8V VDSQ = VDD − IDQ ⋅ Rs 2 ⋅ IDSS 1 IDQ ⋅ = 4,43 ⋅ 10−3 Vp IDSS Ω ⇒ fijada haciendo un gráfico de ID=f(VDS) ⇒ Rs = 330Ω ⇒ VDSQ = 8,04V VGG = VGS + IDQ ⋅ Rs = 2,38V Análisis dinámico: Rd = RS RL = 180,82Ω 1/gm RG Vi gm.vi RS RL Vo R′d = Rd 1 = 100,4Ω gm Vo = gm ⋅ Vi ⋅ R′d AV = IL = Vo = gm ⋅ R′d = 0,445 Vi Vo R ′d ⋅ Vi = − gm ⋅ RL RL Ai = Ii = IL gm ⋅ Vi ⋅ R ′d RG =− ⋅ RG = − AV ⋅ Ii RL ⋅ Vi RL Vi RG 172 Ai = 12 = AV ⋅ RG RL ⇒ RG = 10786,5Ω ⇒ R1 = 54386Ω ≅ 56K Para hallar R1 y R2: R1⋅ VGG = VDD ⋅ RG R2 = 1 = 13360Ω 1 1 − RG R1 ⇒ R 2 = 15K Verficación: RG = R1 R 2 = 11,83K VGG=2,53V gm = 4 ,51 ⋅ 10−3 S ⇒ IDQ=12,47mA Ai = AV ⋅ AV=0,45 RoA = RG = 13,3 RL 1 rd Rs ≅ 130Ω gm Problema 33 Diséñese un amplificador JFET drenaje común como el mostrado en la figura 4 que cumpla las siguientes condiciones: Ai=15, RiA=400K, VDD=12V, RL=20K. Para un punto de trabajo IDQ=2mA y VGSQ=-0,5V , gm=3,33mS. RiA ≅ R1 R 2 = RG Rd = RS1 RL Ii Ai = 15 Vi g s RG 400K gm.vgs d 173 RS1 RL Io 0,5 0,002 = IDSS ⋅ 1 + Vp Vi Ii = RG gm = 3,33mS = − 2 2 ⋅ IDSS 0,5 ⋅ 1 + Vp Vp RS1 Io = − gm ⋅ Vgs ⋅ RS1 + RL IDSS = 4 mA Vp = −1,7V RS1 gm ⋅ RG ⋅ RS1 + RL Ai = − 1 + gm ⋅ ( RS1 RL) ⇒ RS1 RL = − RL ⋅ Ai = 900,9Ω gm ⋅ RG + RL ⋅ gm ⋅ Ai RiA = RG = R1 R 2 = 400K Adopto IDQ ≥ 0,6 ⋅ IDSS : ⇒ IDQ = 2 ,5mA gm = 3,7 mS VGS = −0,36V VDSQ = VDD − IDQ ⋅ ( RS1 + RS 2) Elijo VDSQ = 7V VDD − VDSQ RS 2 = − RS1 ID IDQ ⋅ ( RS1 + RS 2) = 5V ⇒ RS1 + RS 2 = 2 K VGG = VGS + ID ⋅ ( RS1 + RS 2) = 4,36V ⇒ RS1 = 414Ω ≅ 390Ω VGG = VDD ⋅ RS1 RL = 405,4Ω RS 2 = 1,5K R2 R1 + R2 R2 = 0,363 R1 + R2 R1 ⋅ R 2 = 400K R1 + R 2 y R2 ≅ 620Ω R1 ≅ 11 , MΩ 174