1 - Instituto Nacional de Ecología y Cambio Climático
Anuncio

Instituto Nacional de Ecología
Libros INE
CLASIFICACION
AE 003001
LIBRO
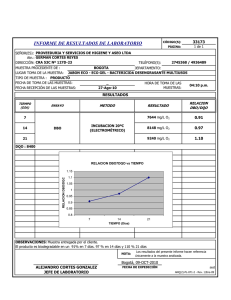
Metodología para determinar las
constantes de desoxigenación (Kd),
remoción de DBO (Kr) y
reoxigenación (K2) en una corriente
TOMO
1111111111111111111111111111111111111111111111111111111
AE 003001
SECRETARIA
DE
AGRICULTURA Y RHUMB_ HIDRA_ ULICOS
SUBSECRETARIA -DE : :PLANEA .CION
DIRECCION GENERAL 'DE
PROTEC. CION Y ORDENACION ECOLOGICA
--~: ~ :'~
DIRECCION GENERAL DE PROTECCION Y ORDENACION ECOLOGICA
Metodología para determinar las constantes de
desoxigenación ( Kd ) , , remoción de DBO ( Kr ) y' reoxige
nación (K 2 ) en una corriente .
1 9 7 7
1
1.
, . . . .E ..2 . .L .sb4á
á
r '
METODOLOGIA PARA DETERMINAR LAS CONSTANTES DE
DESOXIGENACION (KD) ;REMOCION DE DBO(KR) ; Y
REOXIGENACION (K2) EN UNA CORRIENTE
Introducci6n
Dentro de la planeación de la calidad del agua se han desarrolla
do y aplicado modelos que simulan el comportamiento de una corriente - que recibe aguas residuales, El modelo de calidad de agua cubre un amplio ámbito de análisis con variaciones en la cantidad de agua, - condicio - nes de la corriente y variaciones en el tiempo.
Uno de los modelos más ampliamente usados en estudios de ca lidad de agua en corrientes es el de Streeter & Phelphs con algunas modificaciones que complementan el comportamiento real del desecho en el -agua .
Las fórmulas generales del modelo son:
L = Lo ( 1 — é
D : Do e
2'
KRt
/
2
En donde:
D
= Déficit de oxigeno disuelto en el tiempo t . (mg/1)
Do = Déficit de OD inicial (mg/1)
= DBO última
al inicio (mg/1)
K2
= Tasa de reoxigenación (día. -1)
KD
= Tasa de desoxigenación (día -1 )
KR
= Tasa de remoción de DBO (día -1)
t.
= tiempo (dia)
L
= DBO en el tiempo t.
La determinación de las - constantes que componen el modelo es la si
suiente:
2.
Constante de desoxigenación (KD).
Esta constante se refiere a la tasa de degradación combina
da de materia orgánica carbonosa y nitrogenada . La utilización de
oxigeno disuelto en el río sigue una reacción de primer orden cpmo
es el caso de la utilización de OD en el frasco de DBO o en un garra
fón . Por consiguiente la remoción de DBO por bio-oxidación exclusi
vamente, en un tramo determinado de río con características qufmi
cas y biológicas semejantes, se puede determinar en el' laboratorio
haciendo las suposiciones siguientes:
a) La desoxigenación es constante a lo largo del tramo de lacorriente .
/
3
b) La reacción en la corriente y en los frascos es de primer orden.
c) La DBO última es la medición de la materia orgánica total
presente en el tramo de la corriente.
d) Se conservan "condiciones fijas", (Steady State), a lo largodel tramo considerado.
En base a lo anterior se pueden emplear alguno de los meto
dos disponibles que el analista considera más accesible. Todos los
métodos en general se basan en la determinación de la Demanda Bio
química de Oxígeno a intervalos de tiempo iguales que permita cono
cer los incrementos y manejarlos mediante procedimientos matemd
ticos adecuados.
Método de los momentos de
2 .1
Moore, Thomas
y Snow.
Este método ajusta los valores medidos con una curva de primer orden que tiene sus primeros dos momentos
y ;
mty -'
iguales a los de los puntos experimentales . Las ecuaciones que
ex- . .
presan esta condición para una serie de valores (n) de "y" (DBO) son:
n
i=o
n
yiL
QI
e +K D t i
=(n+ 1) L—L
i=o
i=o
_ KDti
n
n
Lti I
(tiyi)
i =0
I—
i =0
n
Lti —
i=0
n
L
ti
i=0
e
K Di
)
dividiendo los momentos se eliminan las L y tenemos:
n
n
yi
n—m
i-0
n
n
(
i :o
e — Ka ti
y i )'
n — K .,t_]
[ti e
ti —
1 =0
Substituyendo en la ecuación anterior para la serie de tiem
i =o
po de 1, 2, 3, 4 y 5 , días y para diferentes valores de KD se obtienen valores diferentes para el miembro del lado derecho ó sea se -obtienen diferentes valores de m yi/ M (tiyi).
De la ecuación (1,) si se elimina el término t=o, y=o y se
expresa
n
yi en términos de L se obtiene.
Í=
n —
n
i=i
e
K°t
Se observa que se puede calcular el término del lado dere - cho para una serie de tiempo de 1, 2, 3, 4, 5, días y para diferentes
valores de KD . Haciendo lo anterior se puede encontrar dos curvas
para esta secuencia de cinco días que permite posteriormente conocer los valores de KD y L . (las curvas se presentan en la gráfica No . 1)
Ejemplo:
Los valores encontrados para la DBO de una muestra a 20°C,
en el laboratbrio, son los siguientes.
Y
(DBO en mg/1)
(días)
ty
82
82
112
224
3
153
459
4
163
652
176
880
686
= 2300.
n
~ yi
686 / 2300 = 0 :299
n
M (tiyi)
Con este valor se entra a la gráfica. No. 1 y se encuentra 1
KD = 0 .23 (en base 10) . De donde KD, = 2.3 ( 0 .23) = 0 .529 (en
base e) .
..
Con el valor de KD obtenido se entra otra vez a la gráfica
y se obtiene el valor de:
=
de donde:
~ y/ L
3 .67
L = 686/3 .67 = 187 mg/1
El mismo procedimiento puede hacerse para una serie de -1, 2, 3, 4, 5, 6, y 7 días . Las caos series mencionadas son las reco
mendadas para su empleo. Estas gráficas se presentan anexas .
2 .2 .
Método simplificado de Thomas Jr.
Cuando no se disponga de las gráficas se puede emplear este-
método, basado en la similitud de las funciones:
I-e Kal= Kt
I-
D
Kt/2 + (
D
K D t ( I-K D t/6) =.~Dt
KD
)2/6--(KDt)3/24+ ..
I-KDt/t ( K r:0 2/6 -(KDt)3/2 .1 .6f. .:
Por consiguiente la ecuación de la DBO puede aproximarse a
la relación:
(
y = L K D t (1 + KD t/ 6) -3
que toma la forma de la recta :
1/3
(t/y
-1/3
=(K
DL )
2/3
1/3
KD / 6 L
+
Si se traza (t/y )1/3 como ordenada contra t como abscisa
el valor de la intersección sobré la ordenada será:
a = (KDL) -1/3
y el valor de la pendiente de la linea recta construida será:
b KD2 /3 / 6 L1/3
Se concluye por tanto que:
KD
-
6 b/a
y
L=
n
7
C.~1
~a 3
f
L .,,,
.4. .0
t~it
~~9 : . «. ~'.~i'a~i11e
.. ..~r.~:
.•, n•
~,
+
. ~
.i li'u
~atM{~
m'-cci.ac+a~a.
Con este método se debe tener cuidado de no usar valores de "y" mayores de 0 .9 L porque la desviación se hace significativa
cuando se ha ejercido el 90 % de la DBO.
Ejemplo:
Tomando los mismos datos anteriores.
t
y
t/ y
(t /y) 1/3
1
.82
0.0122
0 .23
112
0.0179
0.26
153
0 .0196
0 .27
163
0 .0246
0 .29
3
Se grafican y se obtiene a = 0.215 ; b = 0 .02
KD = 0 .56 díá
2 .3 .
-1
; . L = 178 mg/1 . (ver gráfica No . 3)
Método gráfico basado en la remoción de DBO.
Para la aplicación de este método es necesario medir la con
centración de la DBO5 en por lo menos tres puntos de cada segmento,
asr como la velocidad y kilometraje entre cada uno de ellos . Estos datos se grafican en un papel semilogaritmico, teniendo como ordena
das la DBO5 y comp abscisas los kilometrajes o tiempos de paso . Se
ajusta la recta visualmente y se procede al cálculo de KD . En elsi =
guiente ejemplo se ilustra el uso del método .
A
Ejemplo:
Punto
DBO55
( mg/1)
Kilometraje
Velocidad.
(m/ s)
51 .5
0 .21
•
A
12 .0
B
9 .6
43 .3
0.21
8,1
37 .0
0 .21
En la gráfica. No. 4 se presenta la recta ajustada.
a). Pendiente de la recta.
Pend . = Log. 12.0 - Log. 8 .1 = 1, 079 - 0 .9085
14 .5
51 .5
37 .0
= 0 .1705
14 .5
1
Km.
b). Cálculo de KD
U=0 .21 m/s
KD
= 0.21
= 2 .3 0 .1705
14 .5
x 86 400 / 1000
18 .14
Km
KD .= 0.49 día 1 „( en base e )
= 18 .14
Km
día
x Km
.49 día -1
fa = 0
Constante de remoción de DBO (KR ).
3
Cuando la remoción de DBO es producida por otros mecanis.
mos aparte del de biooxidación como son: sedimentación y adsorción,
se debe incluir en el modelo la constante KR . En general KR KD
K3 en donde' la K3 es la tasa de remoción debida
a sedimentación y/o
adsorción . Cuando los fenómenos mencionados no existen la K R es igual a la KD.
El cálculo de la KR se realiza graficando por lo menos tres
valores de DBO 5 por segmento contra el kilometraje o tiempo de pasó.
Ejemplo:
Punto
DBO5
Kilometraje
( mg/1 )
Velocidad
( m/ s )
A
24 .0
62 .8
0 .21
B, .
15 .3 , ,
55 .6
0. 21
C
12.0
51 .5
0 .21
'Se grafica en papel semilogaritmico, se obtiene la recta y se
calcula la pendiente ( ver gráfica No . 5)
Vel . = 0 .21 m/s = 18 .14 Km
dfa
KR = 2.3 Clog 24 .0 - log 12 .0
K R = 1 .1 dfa -1
18 .14 =' 1 .1
11 .3
10
4:
/
Constante de Reaeración (K 2)
La reaeración del agua de un río es un proceso natural de - -
transferencia de masa . La tasa de transferencia de masa de oxígeno
en un río depende de las características del agua, temperatura, del gradiente de oxígeno y del gradiente de presiones parciales, así como
del aire del segmento donde' la transferencia ocurrió . Esta transfe - - .
rencia es del tipo de difusión molecular.
La forma general deducida en base a la primera. Ley Fick es:
K 2 = a Um H -n
en dónde :
U y H = Velocidad y profundidad media respectivamente.
K2
. = Coeficiente de reaeración
a, my n = Parámetros característicos de cada río en párticu
lar.
Para los fines presentes se utilizará la ecuación general de sarrollada por O'Connor, checándose que los valores sean congruentes o cercanos con los valores recomendados para las diferentes ca racterfsticas geométricas de un río.
Fórmula propuesta por O'Connor para una temperatura de 20° C.
= 4 .-0 Ul/2
H3/2
11
en donde :
U = velocidad media en m/s
H
profundidad media en m
Se deberá tener especial cuidado en que las constantes sean
siempre valores de base e para poder utilizar el modelo matemáticodescrito .
y
Ejemplo:
Datos:
Tramo A Velocidad = 0 .21 m/s
Tirante medio = 1 .65 m
1/2
K2 = 4 x (0 .21)
(1, 65) 3/ 2
= 0 .865
Corrección por temperatura
La temperatura es uno de los más importantes factores encualquier sistema biológico . Los cambios de temperatura producen aumento o reducción en la velocidad de reacción así como en la trans
ferencia de oxígeno.
Tanto la prueba estándar dé la DBO como el cálculo de la tasa de reoxigenación se realizan a temperaturas estándar de 20° C .Por consiguiente cuando se quiere conocer las tasas de reacción y --
12
reoxigenación a diferentes temperaturas se emplea la expresión propuesta por Van't Hoff-Arrhenius:
K
-_
20 (
T-20
$ )
Los valores típicos para 6 son:
KD tasa dé desoxigenación:
$ = 1,047
K2 tasa de reoxigenación :
$ = 1,024
KR tasa de remoción de DBO :
1,047
Ejemplos:
= 0 .3 día
-1
(cálculo con alguno de los métodos descritos)
T = 25°C
KD(25) = 0 .3 (1 .047)25-20 = 0 .3 (1 .047) = 0 .3x1 .258=0 .377d1a -1
K2 = 0.86 día -1 (para 20°C); si T=25 °C
K2 = 0 .86 (1 .024) 25-20
0
.97
Corrección por volumen de escurrimiento
Los diferentes volúmenes de escurrimiento afectan a la autopurificación mediante la relación con la tasa de reacción (K2) . In -vestigaciones llevadas a cabo en relación a lo anterior han dado por resultado la ecuación siguiente :
13
/
En donde la tasa de reaeración varía directamente proporcional a una constante "a" y en forma potencial a una constante "b"
para cada río en especial,
Para obtener las constantes mencionadas se debe contar - con un mínimo de tres valores de K2, calculados como se mencionóanteriormente, para tres diferentes Q . En esa forma se puede establecer la ecuación,
log K2 = log a + b log . Q
Los tres valores diferentes se grafican en papel log-log y
se determina los valores de a y b ,
Por consiguiente sé puede calcular el valor de K 2 para di
ferentes gastos de escurrimiento.
7.
Valores recomendados para las constantes
a) Para las constantes de desoxigenación se recomiendan'
valores de 0 .8 a 0.2 dfa- 1 en. base e,
b) Para la tasa de remoción de DBO por sedimentación y
otros valores promedio encontrados son : 3 .0 - 1 .0 - día 4 en base e .
14
c) Para la tasa de reoxigenación se tienen valores promedio de 0 .5 a 12 .2 día- 1 y nunca se toma un valor mayor
de15.
Aplicacion del modelo
Con el fin de aplicar el modelo descrito, es necesario conocer todos los parámetros que lo componen, tales como :DBO5, - I=u, KD, KR, K 2 , oxigeno disuelto, temperatura ambiente y del
agua, velocidades, tiempo de paso, características ffsicas de la corriente y otros valores . Para la obtención de los parámetros reque
ridos es conveniente realizar lo siguiente:
8,1 Trabajos de campo. - El trabajo de campo es de primordial importancia y debe desarrollarse con la mayor exactitud posible .
8.1 .1 .
O
Reconocimiento de la zona . - Se debé recorrer la zona en
una visita preliminar para determinar en forma de croquis
las características hidráulicas y ffsicas que presenta la co
rriente en estudio . ' Se levantarán croquis de presas, caidas, , cambios de sección, puentes, estaciones de aforo, accesos, sección .transversal aproximada, pendiente y = cambios de volumen hidráulico como, descargas de aguaresidual, canales de extracción y afluentes .
15
$ .1 . ~.
/
Localización de descargas de agua residual .- En base a los
datos recopilados y al reconocimiento de zona, se procede a localizar en un plano a escala manejable, todas las descar
gas de agua residual en forma más exacta, mediante mediciones directas relacionadas con puntos fijos de fácil identi
ficación en el plano . Se anotarán también todas las caracte
rfsticas encontradas en el reconocimiento, que no aparez - can en el plano base . Se anotará el Kilometraje existente en cada uno de los datos recabados.
8 .1 .3.
Toma de muestras y mediciones de caudal . - La selecciónde las estaciones de muestreo se efectuará con el criterio
siguiente:
a) En el sitio determinado como inicio del estudio para co nocer las condiciones iniciales.
b) Antes, sobre y después de cada descarga de agua residual.
c) Antes, sobre y después de cada afluente a la corriente en estudio..
d) Antes y después de cada cambio de sección ó de pen - diente.
e) Ala entrada de las presas.
f) A la salida de las presas
g) Antes y después de cada canal de extracción
16
h) En dos puntos intermedios de cada segmento
i) Antes y después de segmentos con actividad fotosintética.
En todos los puntos de muestreo seleccionado se tomarán -muestras de agua y se transportarán bien refrigeradas (4°C
6 menor) para su análisis en el laboratorio . En el campo se determinará : la temperatura ambiente y del agua, oxfge
no disuelto, pH, conductividad, altitud, volumen de escurri
miento, velocidad y tirante del agua.
Para cada segmento del río seleccionado se debe medir sus
condiciones físicas cómo son sección transversal, tirante
de agua y ancho promedio de la corriente . Estas caracte -rfsticas se consideran uniformes en todo el segmento selec
cionado.
8 .2
Análisis de Laboratorio . - Existe un gran número de ele -
mentos y substancias qufmicas que pueden o no alterar las condici - nes físicas y químicas de un agua natural . Gran porcentaje de los - compuestos químicos que se encuentran en un curso de agua nato - - ral, así como en las aguas residuales, corresponden a compuestos
orgánicos . Estos compuestos pueden ser oxidables química y bac - teriológicamente o no oxidables dentro de períodos prácticos del - ingeniero.
El efecto e importancia de los contaminantes más significa-
17
tivos en los cuerpos de agua se pueden encontrar ampliamente desarrollados en diversas publicaciones ; por lo que esta metodología se
limita a las condiciones-de descarga de materia orgánica producidapor localidades e industrias que disponen sus residuos directamente
en una corriente . Por consiguiente los parámetros de laboratorio que se medirán en el laboratorio son : pH, DBO5 , DBO última, tasa
de desoxigenación (KD), DQO y sólidos totales volátiles.
8 .3 Duración de los muestreos y análisis . - Los muestreos y aforos de la corriente en estudio se efectuarán durante un período mínimo de 6 semanas con dos tomas semanales por estación . Lo - anterior nos proporcionará 12 resultados los que son factibles de -analizarse estadísticamente y evaluarse con mayor precisión.
En las descargas de agua residual doméstica e industrial -se recomienda además de los muestreos y aforos rutinarios cada se
mana durante los tres meses, un muestreo de 24 horas con intervalos de 4 horas en donde se analizarán las muestras individuales y la
compuesta . El muestreo de 24 horas se deberá realizar en un día de trábajo o funcionamiento normal.
r
/
18
Cálculo de parámetros que intervienen en el modelo
9 .1 .
Oxígeno Disuelto
El valor de oxígeno . disuelto que se emplee en el modelo será
el determinado estadísticamente por el percentil 25 en base a los da - tos obtenidos en el campo.
Ejemplo: Datos de los 12 muestreos (mg/1) : e . 2; 5 .4 ; 7 .1 ; 6 .5 ; 7 .2 ; 6.4 ; 5 .9; 6 .8; 6.6 ; 7 .0; 6 .8; 6 .6.
Se ordenan en forma ascendente.
5 .4,
Numero de datos.
6 .2
6 .4
6 .5
6 .6
6 .6
6 .8
6 .8
7 .0
7 .1
7 .2
Percentil 25 =
5 .9
9 .2
Valor del P25
=
12
12
x 25
100
= 6 .2 mg/ l
Demanda Bioquímica de Oxígeno
La . Demanda *Bioquímica de Oxígeno que se utiliza en
el modelo
es la llamada de término largo o DBOu . En virtud de lo anterior se de
be obtener la relación de DBOu
a DBO5 cuando se determine la K D .
Este valor se empleará después con el valor de DBO 5 seleccionado - que será para cada punto a analizar, el Percentil 75 de los válores de campo medidos.
19
Ejemplo:
1)
En la determinación de la KD se encontró una DBO5 = 50 mg/1
y una DBOu = 64 mg/1. Relación DBOu/DBO5 1 .28
Datos de campo : (DBO5 de los 12 muestreos tomados)
52, 47, 40, 71, 58, 49, 51, 10, 46, 50, 54, 48, mg/1.
Se ordenan:
12
10
Percentil 75 =
x 75
40
100
46
49 El valor del Percentil 75 = 52 mg / 1
48
49
DBO 5 = 52 mg /1r (valor a emplear en el modelo)
50
51
DBOu = 25 x 1 .28 = 66 .5 mg/1 (valor a emplear en el modelo)
52
54
58
71
9 .3
Volumen de escurrimiento
El gasto utilizado en el modelo depende de la etapa que se rea
lice del. mismo . Para la calibración del modelo se utiliza el gasto me
dio durante la etapa de muestreo y mediciones de campo . Lo anterior
sirve para ajustar las constantes tanto de desoxigenación, remoción de DBO 6 reoxigenación . Una vez calibrado el modelo se puede em- plear en condiciones críticas de escurrimiento . Para fijar condiciones
particulares 6 cualquier otro estudio de evaluación, se debe emplear el promedio de los gastos mínimos diarios de cada mes registrados en
los boletines hidrológicos durante los últimos cinco años .
/
20
Efecto de la carga bental.
10.
Cuando el agua residual lleva muchos sólidos `en suspensión capaces de sedimentarse, se efectúa una remoción más rápida de la DBO por este fenómeno y se obtiene la tasa
KR
en ese tramo . Sin -
los sólidos sedimentados ejercen una DBO en el agua que es -
embargo
curre encima de ellos.
Esta carga debe ser considerada y agregada al modelo cuan,
do este fenómeno sucede . El . término que se agrega en forma de suma es :
HK2'
I
en donde :
DSB
= Déficit originado por la carga bental
= Tasa de reoxigenación
SB
.
= Demanda de los lodos bentales en grs 0 2
m2 x dfa
t
= Tiempo
Profundidad
media de la
corriente
Cuando ,el fenómeno de sedimentación descrito tiene lugar en una corriente la ecuación general se cs nvierte en:
–K2t
D = Doe +
K o ~o
K2-K R
-KR'
- K 2t
e —e
+
SB
K2H
El ámbito de valores encontrados para la demanda de lodos -bentales
es :
21
Consumo de Oxígeno
s B = gr de 02
m2 x día
Tipo de Lodos
11 .
/
Ambito
Promedio
Lodos municipales
2 - 10
4
Lodos municipales "viejos"
1 -2
1 .5
Fibra de celulosa
4 - 10
6
' Otros parámetros
Existen otros parámetros que afectan las concentraciones de
oxígeno en una corriente . En cada uno de los casos el ingeniero ambiental debe de utilizar su criterio y experiencias para incorporarlos
a la ecuación general en caso de que éstos se presenten en la corrieñ
te y sean significativos para el comportamiento de las característi-ca.s de calidad de la corriente . Los fenómenos que se pueden presen
tar
son la fotosíntesis y respiración de plancton y la demanda bioquí
mica de la materia orgánica nitrogenada.
11 .1 . Demanda bioquímica de la materia nitrogenada
Cuando este fenómeno se presenta el déficit de oxígeno ocasionado se calcula con la expresión.
4. . 57
Kn No
22
en donde:
Kn
= Tasa de desoxigenación de la materia orgánica nitrogenada.
No
= Concentración de materia orgánica nitrogenada inicial
Tiempo
Tasa de reoxigenación
Fotosíntesis y respiración
11 .2.
La solución general para estos dos fenómenos es:
DF :
Pa :
en donde :
(R— Pa
r1_ ~ '•
2
K2
fp24 x
1T
P
max .
DF
= Déficit de oxígeno por efecto de fotosíntesis y respiración.
R
= Consumo de -oxígeno por la respiración del plancton . (mg/1
x día).
P
max=
P- roducción máxima de oxígeno por efecto de la fotosíntesis
(mg/1 x día)
K2
=- T
asa de reoxigenación
tp de producción
Tiempo
t
12 .
=- T
iempo de paso
Ejemplo práctico
Una industria descarga agua residual en un río . La norma -
de calidad indica que el nivel mínimo de oxígeno disuelto no puede ser
menos dé 4 .0 mg/1 en condiciones de estiaje . Se requiere determinar
23
el nivel de tratamiento actual y el futuro para una expansión de la indus
tria del 60 % en su producción . Datos del muestreo intensivo de 12 da
tos (12 semanas, 1 vez por semana ; 6 6 serranas 2 veces por semana).
12 .1 .
Características de la corriente : datos medidos en campo.
A
Estaciones de
Muestreo
B
C
D
E
F
!
~Iw
bp
ir)
M
~)
d
IiT
G
1
Punto 0
~
w.
~
1f)
co
gasto ( A - E )
= 2 .17 m3/s
gasto T
= 1 .13 m3 /s
Temperatura media
= 25° C
'Oxfgeno de
saturación
1!{T
ti
M PM M
i
ti
_
= 8 .2 mg/i
Profundidad ( A - G ) = 1 .65 m
Demanda de lodos
bentales = 2
gr
m2 x día
DBOu = 1 .43 DBO5
Altura sobre el nivel del mar: 10 m
Aguas Arriba (punto 0):
DB05
= 1 .8,1 .5,2 .0,2 .1,2 .0,1 .9,1 .7,1 .8,2 .0,1 .9,2 .1,2 .0
OD
= 7 .5,7 .0,7 .4,7 .2,7 .4,7 .8,7 .5,7 .4,7 .8,7 .5,7 .6,7 .8
Kilometraje
24
Percentil 75 de la DBO5 : Se ordenan los datos en forma progresiva
1 .5
-1 .7
1 .8
1 .8
1 .9
1 .9
2 .0
2 .0
2 .0
2 .1
2 .1
3 .0
P75 .
P75
DBO5
= 12x_75/ 100
= 2 .0 m/ 1
= 2 .0 mg/ 1
=
9
Percentil 25 del OD : Se ordenan los datos en forma progresiva
7 .0
7 .2
7 .4
7 .4
7 .4
7.5
7 .5
7 .5
7 .6
7 .8
7 .8
7 .9
P25
P25
OD
=12x25/100=3
= 7 .4m / 1
= 7 .4 mg/ 1
De acuerdo al recorrido realizado y a los criterios descritos se
seleccionaron 3 tramos o segmentos de la corriente . Tramo A - C;
Tramo C-T; Tramo T-G . De la misma forma se seleccionaron- 8 pun
tos de muestreo sobre las corrientes y otras sobre la descarga indus
trial. .Los valores obtenidos en cada punto se analizaron en la misma
forma que la estación original y los percentiles 75 para la DBO5 y - los percentiles 25 para el OD, fueron los siguientes:
Pu n to
DBO5
( mg/i )
OD
( mg/1 )
Kilometraje
A
B
C
D
E
T
F
G
24 .0
15 .3 .
12 .0
9 .6
8 .1
0 .0
4 .8
3 .8
7.0
2 .1
1 .0
0 .8
1 .0
8 .2
3 .8
4 .6
62 .8
55 .6
51 .5
43 .3
37 .0
36 .7
30 .8
17 .7
Vel
(m /
:
-
0. 21
0.21
0 .21
0 .21
0.21
0.32
0 .32
25
12.2 .
Datos de condiciones de estiaje
Gastos mínimo anual (A - E) = 1 .42 m 3 /` s
Gasto T = 0 .71 m3/s
Profundidad (A - C) = 1 .16
Temperatura
30°C (OD = 7 .6)
Altura sobre nivel del mar =_10m
12 .3 .
Datos de la descarga
Muestreo cada 3 hr durante 24 hr . (8 resultados) gasto en lps:
Q Ips
D
80
::;;H":;~'
6
Q medio = 100
DBO5
12
18
lps
(promedio) = 500 mg/1
OD=0 .0mg/1
24
600
DB0 5
400 mg/ I
200
Hr
.
3
92
6
134
9
129
12
112 .
15
88
18
83
21
82
26
12 .4 .
Determinación de constantes (K D , KR , K2)
a) En papel semi-logarítmico graficar los valores de DBO5 en el eje de ordenadas (escala logarítmica) y los kilometrajes ep
las abscisas.
L = Lo .e KRt= Loe —KR
log L — Log Lo
K R = 2 :3
= KR
u
f
log Lo - log L
+
Tramo A - C
Lo
= 24 .0 mg/ l
= 12 .0 mg/1
= 62 .8 - 51 .5 = 11 .3 Km
U
= 0 .21m/s = 0 .21x86400x10 -3
= 18 .14Km/día
= 2 .3 og 24 .0 - log 12.!x 18.14
11 .3
L
1 .11 día. -1
Tramo C -E
KD
= 2 .3 log 12 .0 - log 8 .1 x 18 .14 = 0 .49 día -1
Tramo F - G
KD
= 2 . 3 Fog 4 . 8- log 3 . 8 x 27 . 65
13.1
0 .49 día - 1
27
Tasa
12 . 5 .
4U
K2
de reoxigeriación
1/2
H 3/2
Tramo A - E
x 0 .4582 = 0 .865 día71(á 200 C)
.1194
x(0 .21)1/2
K2
2(1 .65) 3/ 2
=
=
Tramo
F-
G
K2 ` 4x(0. 32)
1/2
= 1 . 067
día -1
(1 . 65)3/2
12 .6
Corrección por temperatura:
temperatura 25 ° C
-1
KR
= 1 .11 (1 .047) 25-20
= 1 .38 d1a
25-20
K2
0 .864 (1 .024)
. = 0 .97 día -1
Tramo A - C
Tramo C - E
KD
K2
= 0 .49 (1 .047) 25-20
= 0.61 día -1
0 .97 día -1
Tramo F - G
KD
_ 0 .49 (1 .047)25 -20
K2
1 .067 (1 .024) 25-20
= 0 .61 día -1
= 1 .20 día -1
28
Calibración del modelo
12 .7 .
Cálculo de Do
Concentración de OD en la mezcla
ODM
=
= 7.4x2.17+0 .1x0
= 7 .07mg/ 1
2 .27
Do
8 .2 - 7 .07 '= 1 .13 mg/ 1
Cálculo de Lo
DBOS =
Qw DBOSw +Qo DBO$
Qw , + Qo
DBOS = 0 .100x500 +2 .17x2 .0 = 23 .938 mg/ l
2 .17 + 0 .1
= 1 .43 x 23 .9 = 34 .2 mg/1
Con estos datos se obtienen los valores' del déficit mediante el
empleo del modelo matemático planteado.
DBO en el punto C
L
= Lo e —
K R + = 34 .2 x 0 .423
14 .46
Do = 7 .09
En el punto T
L
=
Loe K R
ú ' =14 .46x0.61 = 8 .63
OD = 1 ..2 mg/ l
Balance de masa al entrar el afluente T
8 .63 x 2.27 + 0x 1 .13
2.27+ 1 .13
= 5 .76 mg/1
29
1 .2x2 .27+8 .2x1 .13 = 3 .52 mg/1
2 .27+ 1 .13
Do = 8 .2 - 3 .5 = 4 .7 mg/ l
Ob =
Todos los valores calculados por el modelo se presentan en la
tabla No . 1 y se comparan con los datos de campo en la gráfica No . 6.
Condiciones particulares
12 .8.
a)
Datos de estiaje
Caudal A - E = 1 .42 m3/seg
Gasto T = 0 .71 m3/seg
Profundidad (AG)
= 1 .16 m.
Velocidad (AE)
= 0 .18 m/s = 15 .55 Km/día
Temperatura = 30° C
OD saturación = 7.6 mg/1
b)
Corrección de constantes por temperatura
Tasa de remociónK R . - En virtud de que cuando se trate el
agua no habrá sólidos en suspensión que puedan sedimentarse
=
KR
KD
1
=
KR
KD
,= 0 .69 (1 .047) 30-20 = 0.77
día
(30)
(30) ,
Tasa de reaeraci6n K2
K2
=
4 (0 .18)1/2
= 1 .36
1
día
(1 .16)3/2
K2
(3Ó)
= 1 .36 (1 .024) 30-20
1 .72
1
día
30
c) Cálculo. de DBOu permisible
Por tanteos se determina el tiempo crítico (te) para ser sustitui
do en la ecuación de la DBOu (Lo)
ler . Tanteo; hacer D° = 0 .15
Lo
tC
IL _ Do
_
.K2_KR L n
KR
K2-KR
Lo
KD
Aplicando los valores obtenidos y Do/ L o = 0 .15 (ver tabla, No. 2)
se obtiene:
= 0 .628 día
Xc = Vxt c = 15 .55 dfa x0 .628 día =9 .76 Km
I
Por lo que el déficit crítico se presenta en el Kilómetro:
62.8 - 9 .7 = 53 .1 Km
Para mantener una concentración de OD = 4 .0 mg/1 se tiene que
el valor de Dc es igual a:
= Cs - 4 .0=7 .6 -4 .0=3 .6mg/l
1
Restando el déficit originado por las condiciones iniciales.
Dc
Dc
= Doe -K2tc
=1
.13 e-1' 72 x 0 .628
= 0 .383 mg/ l
2
Por lo que :
Dc
= 3 .6 -0 .38 =3 .,22 mg/ 1
31
/
/
Sustituyendo estos valores en la ecuación de la DBOu
K2
Dc
_ 1 .72 x 3 .22
= 11•.658 mg/1
-KDtc
-0 . 77 x O . 628
KDe
0 .77 xe.
Se calcula Do / Lo para comprobar:
Do
Lo
1 .13
11 .658
0.097 < 0 .15
Este valor es menor que el 0 .15 del primer tanteo por lo que
se procede al 2o . tanteo con Do/ Lo = 0.1 y se obtiene tc =
0 .704 día (ver tabla No . 2) ; 'Cc = 15 .55 x 0.704 = 10.94 Km y
la distancia a la cual se presenta el déficit critico 51 .9 Km.
Dc= 3 .6 =1 .13e
Lo =
-1 . 72 x 0.704
=3 .26
1
día
1 .72 x 3 .26
= 12 .52 . mg/1
-0 . 77 x 0 . 704
0 .77. x e
Segunda comprobación
Do
Lo
_ 1 .13 = 0 09 0
.10 Se acepta
12 .52
'
La DBOu de la mezcla es por tanto de 12 .52 mg/1
La DBO5 de ' la mezcla es : 12 .52/1 .43 = 8 .75 mg/l
La carga permisible al río en el punto de la descarga y en términos de DBO5 es :
/
32
3
8
6,400
.seg
(8 . 75 - 2 . 0) LL x i2 . ms x 103m 3
1
día
x 10 -6 Kg= 828 Kg /día
mg
Lo que da una DBO5 permisible en la descarga de:
DBO5 x 100 x 86, 400 x 10 -6 = 828 d
a
n
DBO
828 = 95
.83 mg/1 (máxima permisible en la descarga)
5 = 8. 4
carga orgánica actual que tira la industria:
w = 500 x 100 x 86,400 x 10-6 = 4 320 Kg/día
Porcentaje de remoción necesario para la' carga actual.
remoción = (4 320 = 828)
80 .8
x 100 =
4320
Este porcentaje obliga a un tratamiento secundario . Por consi-guiente, la base para los demás parámetros es lo que remueva un
tratamiento secundario de` esta magnitud.
Para las condiciones futuras:
Porcentaje de expansión 60 %
carga orgánica futura.
w = 4320 + 0 .6 (4320) =6912 1Kg/día
_
de remoción = (6912 828)x 100 = 88 %
6912
Para el futuro necesita un tratamiento secundario que pueda remo
ver el 88 % .
Fig ura Ns 1
.242
6 .00
:238
5 .60
.234
5 .20
my/aty
4 .80
.230
.226
4.40
3EY/atY
.222
4 .00
.218
3 .60
.214
3 .20
.210
2 .80
.206
.05
.10
.15
CONSTANTE
.20
DE
VELOCIDAD
.25
.30
.35
2 .40
DE REACCION " K "
Valores de " K " y de la DBO última para series, de pruebas de la DBO por
1,2,314 1516 y 7 días (según Moore, Thomas y Snow )
Figura- N° 2
.310
420
.306
380
f y/L
.302
E y /f y
340
.298
200
EY /~t y
.294
f
y/L
260
.290
220
.286
1 .80
.282
1 .40
.278
05
.10
_
15
CONSTANTE
Valores
. 20
.25
DE VELOCIDAD DE REACCION
.30
35
K"
de " K " y de la DBO última para series de pruebas de la DBO por
1,2,3,4, y 5 días
(según
Moore, Thomas y Snow )
DETERMINACION DE K D y L POR EL METODO SIMPLIFICADO DE THOMAS J
Gráfica N2 3
DATOS
(t/y)'13
t
.30
I
2
.29
0.2 3
'0 .26
0 . 27
0 .29
3
4
.28
.27
.26
'(t/y~
.25
a=
.24
b = 0 .02
.23
K D=
0 .215
6b =
a
1
.22
KD a 3
.21
.20
I
2
3
5
t (
diaS )
6x0.02/0 .215=0.56 día -1
=
1
0.56x ( .215)3
=
178 my/ I.
100
90
80
Gráfico N $ 4
70
CALCULO DE KD
60
50
40
30
20
Punto A
5
DATOS
4
OB05
12 .0
9.6
8.1
3
KMS.
51 .5
43.3 37.0
= 0 .49 día —1
2
K0=2 .3
L log 12 .0 — log 8 .1 1 x18 .14=049 día-1
51 .5—37 .0
1
55
50 ,
40
30
KILOMETROS
20
100
90
.80
Gráfica N 5
70
KR
CALCULO DE
60
~ `. ..`F7_1 . ..
50
40
~ _._. ._~
. .<..~. .
:
~.
~
.
T
}~T ~
t
YdC~
u
-w
30
20
Punto C
8
7
6
5
DATOS
4
Punto
DBO~
KMS .
VEL.
Pendiente
A
B
C
3
24.0
15 .3
12.0
629
55 .6
51 .5
0 .21
0 .21
0 .21
=
log 24 - log 120 ]
0 .301
62.8 - 51 .5
K R =' 2 .3x
0 .301
11 .3
I
km.
x 18 .14 = I .I día —1
11 .3
2
Para convertir la . K R de base 10 a K R base e
se multiplica por 2 .3
65
60
55
50
KILOMETROS
Gráfica N°6
CALIBRACION DEL MODELO
io —
CURVAS DEL MODELO
O
'l
60
1
A
50
B
. PUNTOS DEL MUESTN®
t
\
40
C
30
ET
KILOMETRAJES
F
20
6
TABLA N 2
1
2
3
TRAMO
K R
K D
4
5
6
1 RESULTADOS DEL MODELO
. 7
8
K2
.
.
( km)
,
km/ día
K R
u
9
t-
K2
10
fi
It
e -K R
ú
éK2
12
ú
13
14
é KRú e -K2
Lo
KoLo
'AB
1 .38
0. 61
0. 97
7. 2
18 .14 0 . 397
0.54
0 .385
0 .582
0 . 68
- 0 .098
34 .0
20 .74 ,
BC
1 .38
0,61
0 .97
11 .3
18 .14 0 .623
0 .86
0 .60
0 .423
0.54
-0.117
34 ;0
20 .74
CD
0.61
0.61
0 .97
8 .2
18 .14 0 .452
0 .275 0.438
0 .759
0.645
0.114
14 .46
8 .82
DE
0 .61
0.61
0 .97
14 .5
18 .14 0 .80
0 .488 0 .776
0 .613
0 .46
0 .153
14 .46
8 .82
ET
0 .61 ,
0 .61
0 .97
14 .8
18 .14 0 .81
0.494 0 .785
0 .61
0.456
0.154
14 .46
8 .82
TF
0.61
0 .61
1 .20
5 .9
27 .65 0.213
0 .13
0.285
0.878
0.775
0 .103
5.76
3 .51
FG _
0.61
0 .61
1 .20
19 .0
27 .65 0 .687
0 .419 0 .824
0 .657
0 .438
0 .219
5 .76
3 .51
15
TRAMO K 2 -K R
16
K2-KR
17
18
19
12 x I6
Do
II x 18
20
I- e K 2
AB
-0 .41
-50 .58
4 .98
1 .13
0.77
0 :32
BC
-0 .41
-50 .58
5 .91
1 .13
0 .62
0.45
CD
0.36
24.5
2.79
7.09
DE
0 .36
24 .5
3 .74
ET
0 .36
24 .5
TF
0 .59
FG
0 .59
21
ú
SB
HK2
22
23
24
D SB
D
17 + 19 + 22
0D
mg / 1
20 x 21
25
Punto
1 .25
0.40
6.15
2.05
B
1 .25 _
0.56
7 .09
1 .1
C
4 .57
7.36
0 .84
D
7.09
3 .26
7 .00
1 .2
E
3 .77
7.09
3 .23
7 .00
1 .2
T
5 .95
0 .612
4.7
3 .62
4 .23
3 .97
F
5.95
1 .30
4 .7
2 .05
3 .35
4 .85
G
_
TABLA N 2 2 CALCULO DE LA DEMANDA BIOQUIMICA DE OXIGENO PERMISIBLE
N° de
K
2
K
R = KD
TANTEO
2
1
- KR
K2 —K R
~
Do
K2- K R
K R
Lo
KD
Do
D
K 2- K R
L0O
K
~
-0
lo x©
In
II
~
0
tc
12
días
1 .72
0 .77
0.95 1 .052
2.23
0 .15
1 .233
0.185
0 815
1 81
~
•
~ . :
1 .72
0.77
0.95 1 .052
2 .23
0.10
1 .233
0 .123
0 .877
1 .955
0.67
0 .704
NACIONAL