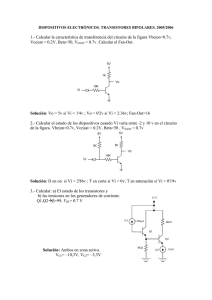
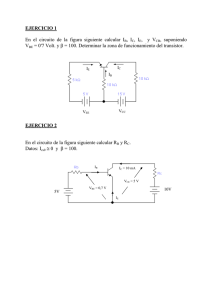
EJERCICIO 2 En el circuito de la figura siguiente calcular RB y RC

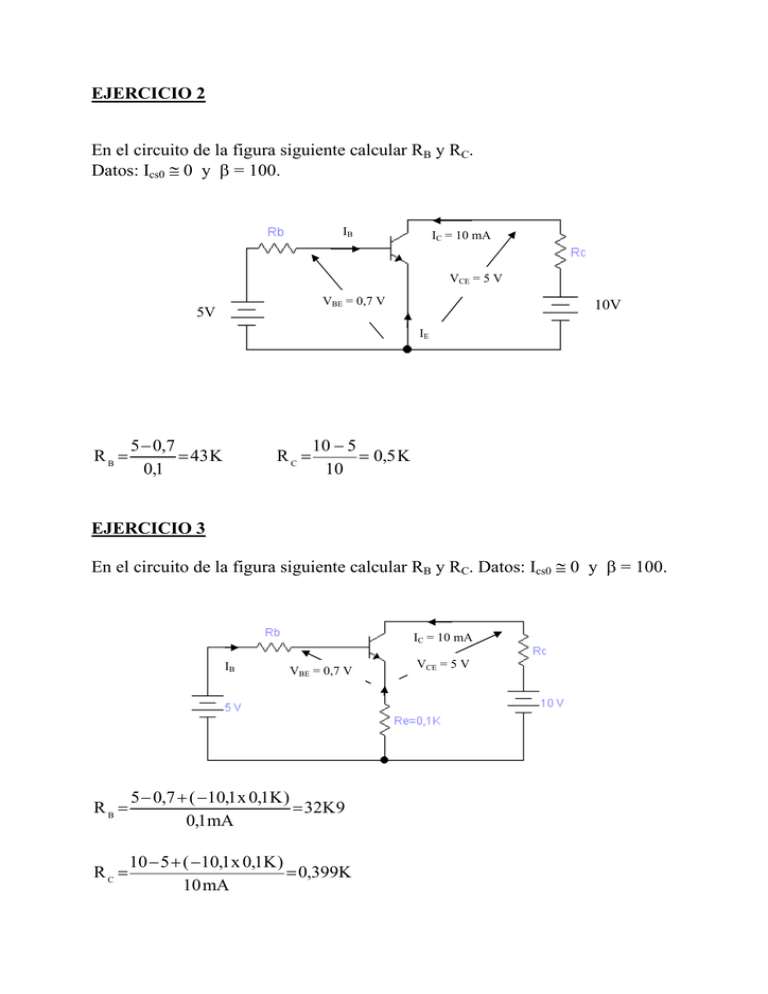
EJERCICIO 2
En el circuito de la figura siguiente calcular RB y RC.
Datos: Ics0 ≅ 0 y β = 100.
IB
IC = 10 mA
VCE = 5 V
VBE = 0,7 V
5V
10V
IE
RB =
5 − 0,7
= 43 K
0,1
RC =
10 − 5
= 0,5 K
10
EJERCICIO 3
En el circuito de la figura siguiente calcular RB y RC. Datos: Ics0 ≅ 0 y β = 100.
IC = 10 mA
IB
VBE = 0,7 V
RB =
5 − 0,7 + ( −10,1 x 0,1K )
= 32K 9
0,1mA
RC =
10 − 5 + ( −10,1 x 0,1K )
= 0,399K
10 mA
VCE = 5 V
EJERCICIO 4
En el circuito de la figura siguiente calcular la tensión colector base si α = 0,98
y consideramos despreciables VEB y ICs0.
IE
IC
VCB
VCB = - 18 + 3,92 x 3k = - 6,24 V
EJERCICIO 5
En el circuito de la figura siguiente calcular la tensión de salida VS suponiendo
despreciable ICs0 y siendo VEB = 0,7V y α = 0,98.
IC
IE
VEB
VCB
IB
VS = IC . RC – 12 = 4 . 1,4 mA – 12 = - 6,4 Volt.
VS
EJERCICIO 6
En el circuito de la fig. siguiente calcular el valor de R1 si ICs0 = 0, VEB = - 0,7V,
α = 0,98 e IE = 3 mA.
C
IR1
IC
B
IB
IE = 3mA
VBE
IR2
R1 =
M
VR1
7,86 V
=
= 62,3 k
I R1 0,126 mA
EJERCICIO 7
El transistor de la fig. siguiente es de silicio. Calcular corrientes, tensiones y
potencias. α = 0,99, ICS0 = 10-6 mA.
IB
IC
VCE
VBE
IE
IB =
− VBB − VBE −1− (− 0,7 )
=
= − 0,15 mA
RB
2
I C = 99 . (− 0,15) − (1 + 99 ).10 −6 = − 14,85 mA
IE = - IC – IB = - ( - 14,85) – (- 0,15) = 15 mA
VCE = - 6,51 Volt.
VCB = VCE – VBE = = - 5,81 Volt.
PBB = VBB X IB = 1 X 0,15 = 0,15 mW
Potencias cedidas
PCC = VCC X IC = 8 X 14,85 = 118,8 mW
PRB = RB X IB2 = 2 X 0,152 = 0,045 mW
PRL = RL X IC2 = 0,1 X 14,852 = 22,052 mW
Potencias consumidas
PJ1 = VBE X IE = 0,7 X 15 = 10,15 mW
PJ2 = VCB X IC = 5,81 X 14,85 = 86,27 mW
EJERCICIO 8
El transistor de circuito de la fig. siguiente es de silicio y tiene una β = 100.
Calcular: IB, IC, IE, VCE y VCB. Determinar la zona de trabajo del transistor.
IE
VEB
IC
IE
VCB
VBC = - 6,73 Volt.
El transistor está en la zona activa, pues:
a) La unión de emisor está polarizada directamente pues VBE > 0
b) La unión de colector está polarizada inversamente pues VBC < 0
EJERCICIO 9
Determinar el valor de las resistencias R1, R2 y R3 en el circuito de la fig.
Datos:
I1
IB
VCC = 20 Volt.,
I1 = 13,75 mA
VZ = 12 Volt.,
rz = 22 Ω
VEC = 4 Volt.,
IE = 2,5 mA
VEB = 0,7 Volt.,
β = 99
ICS0 = 0,
VCE(Sat) = 0
IE
IZ
IC
R1 =
VCC − VB 20 −12,3
=
= 0,56K
I1
13,75
R2 =
VCC − VB − VEB 20 −12,3 − 0,7
=
= 2K8
IE
2,5 mA
R3 =
VCC − I E . R 2 − VEC 20 − 2,5 mA . 2,8K − 4
=
= 3636 Ω
βI B
99 . 25.10 −3
EJERCICIO 10
En el circuito de la fig. siguiente, hallar la zona de funcionamiento del transistor.
DATOS:
VBE = 0,7 Volt β = 100
I
VCE = 10 – 1,252 – 2,48 = 6,267 V
Como VCE > 0 el transistor trabaja en la zona activa.
EJERCICIO 12
Comprobar si el transistor T1 del circuito de la fig. siguiente está saturado y
calcular las tensiones y corrientes del transistor T2. Suponer hFE(min) = 40,
VBE = 0,7 y VCE(Sat) = 0,2 V.
IC1 = 9,8 < 40 . 0,28 = 11,27 mA = hFEmin x IB lo que demuestra que el transistor
T1 está saturado.
Al estar T1 saturado y como VCE(Sat) es una tensión inferior a los 0,7 V que
necesita T2 para conducir, este permanecerá al corte. Por lo tanto tenemos que:
IB = 0
IC2 = 0
VBE2 = 0,2 V
VCE = VCC = 10 V
EJERCICIO 13
Diseñar el circuito de la fig. siguiente para que el transistor funcione entre corte
y saturación cuando se aplique una señal cuadrada cuyos valores extremos sean
de 0 Volt. y – 5 Volt.
Datos:
VBE (Sat.) = - 0,7 V
VCE (Sat.) = 0 V
IC (Sat.) = 20 mA
hFE = β = 90
0V
-5 V
RC =
VCC − VCE (Sat )
RB ≤
IC
≈
VCC
IC
=
−5
20.10 −3
= 250 Ω
90 . 4,3
=19350 Ω
20 .10 −3
por lo tanto, cualquier valor de RB por debajo de 19350 Ω saturará al transistor.
EJERCICIO 14
Calcular el valor de la tensión en V0 en las dos posiciones del circuito de la fig.
siguiente.
B
A
Datos: hFE = 100, VBE = 0,7
VCE (Sat.) = 0,2 V
T1 = T2
POSICION A:
V0 = VCE 2 − VBB = VCE (sat ) − VBB → V0 = 0,2 − 3 = − 2,8V
POSICION B
T1 está saturado, D Z no conduce y T2 está trabajando al corte, por lo que en
estas condiciones V0 = VCC = 12 Volt.
EJERCICIO 15
En el circuito de la fig. determinar la zona de trabajo del transistor en los
siguientes casos:
a) E = 0,4 Volt.
b) E = 10 Volt.
Datos:
IC
IB
IE
VCE Sat. = - 0,2 Volt.
VBE = - 0,7 Volt.
β = 50
a)
Como VBE < VEBγ = 0,7 Volt. el transistor trabaja al corte.
b)
El transistor está en la zona activa.
EJERCICIO 16
Analizar los dos circuitos siguientes, e indicar si se encuentran trabajando en la zona activa o
en saturación.
Datos: hFE = 100, VCE(Sat) = 0,2 Volt., VBE(Sat)= 0,8 Volt., Rb = Amarillo-Negro- Naranja
Rc = Rojo - Rojo – Rojo Re = Verde – Negro - Rojo
Circuito (A)
Circuito (B)
SOLUCION:
Circuito (A):
El transistor está saturado, pues la corriente real de base del transistor es mayor que la
corriente de base en saturación 0’1 mA > 0’044 mA
Circuito (B):
El transistor no está saturado, pues la corriente real de base del transistor es menor que la
corriente de base en saturación , 0’007 mA < 0’0136 mA
EJERCICIO 17
Para el circuito de la fig. siguiente, calcular el mínimo valor de RC para que el transistor
permanezca en saturación
12 V
RC
RB
VBB
Solución
El valor mínimo de RC = 5K7
Datos.Transistor de silicio
VBE Sat. = 0,8 Volt.
VCE Sat. = 0,2 Volt.
β = 90
VBB = 7 Volt.
RB = Rojo - Violeta - Amarillo
EJERCICIO 18
En el circuito de la fig. siguiente, el transistor es de silicio, siendo su βcc = 80. Calcular la
corriente por el zener así como la potencia disipada por el transistor.
Zx10
IZ = 14,7 – 7,75 = 6,95 mA
1) Pdt = 6,56 W
EJERCICIO 19
En el circuito de la fig. siguiente, calcular los valores de RB y R1 de manera que el transistor
I
esté saturado con una relación C = 20, si la corriente por el LED es de 20 mA.
IB
Datos:
Rele (12 V, 200 Ω)
LED (VLED = 2 V)
Diodo (Vγ = 0,6 V)
Transistor (VBE = 0,6 V, β = 120)
RB = 1,1 K
R1 = 500 Ω
EJERCICIO 20
En el circuito de la fig. siguiente, calcular el valor de RC que situa al transistor en la frontera
entre la zona activa y saturación.
Datos:
VB = 6 V
RE = 200 Ω
Transistor (VBE = 0,6 V, β = 89)
RC = 0,539 KΩ