Articulo P3 G9NL24
Anuncio

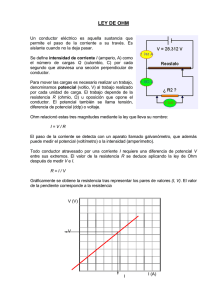
Fundamentos de Electricidad y Magnetismo, Mayo de 2010 Diferenciación de resistencias de acuerdo a sus propiedades y características Differentiation of resistance according to their properties and characteristics Henry Mauricio Ortiz Osorio cód. 200853 G9NL24 Universidad Nacional de Colombia, Bogotá, Col. 26 de Mayo de 2010 Resumen El presente documento pretende realizar una explicación clara del concepto de resistencia eléctrica y su asociación con la conductividad eléctrica, además de establecer la relación que existe entre un material y su resistencia eléctrica, mencionando los diferentes factores que influyen en la resistividad, tomando como eje central la diferenciación entre las resistencias óhmicas y las no óhmicas, ilustrando el modelo físico que vincula la corriente con el voltaje en este tipo de resistencias. Palabras Claves: resistencia no óhmica, temperatura. Abstract This document is intended to make a clear explanation to the concept of electrical resistance and its association with electrical conductivity as well as establishing the relationship between a material and its electrical resistance, noting the various factors affecting the resistivity, on the central axis differentiation between the ohmic and non-ohmic resistances, illustrating the physical model that links the current with voltage in this type of resistance. Keywords: non-ohmic resistance, temperature. En Electricidad y Magnetismo, la resistencia se define como la propiedad física de un conductor que mide la oposición que presenta este mismo al paso a su través de un flujo de electrones, las unidades que se usan para denominar la resistencia en el Sistema Internacional de Medidas son los Ohmios, y estos son definidos a su vez como la resistencia de una porción del circuito entre cuyos extremos existe una diferencia de potencial de un voltio, cuando la intensidad de corriente que lo atraviesa es de 1 amperio, lo inverso de la resistencia es denominado conductancia. Con lo que se tiene que para que la resistencia sea constante no sólo es preciso que el conductor conserve su forma y dimensiones, sino que debe estar colocando en las mismas condiciones físicas, especialmente a la misma temperatura [1]. Debido a lo anterior se sabe que la resistencia de un conductor aumenta con su temperatura, debido al aumento del número de choques entre los electrones y los átomos. Ésta es la condición general para la mayoría de los metales. Sin embargo, compuestos como el carbono y el vidrio poseen un coeficiente de temperatura negativo, razón por la cual su resistencia varía en sentido contrario a su temperatura. Para los diferentes compuestos se tiene una resistencia específica denominada resistividad que viene determinada por la estructura molecular del material y por su temperatura. En el Sistema Internacional de Medidas, esta característica está expresada cuantitativamente en Ohmios por metro, por lo cual la resistencia de un conductor homogéneo, de longitud “l” y sección constante “s” se puede calcular por la expresión que establece la segunda ley de Ohm también denominada ecuación de Pouillet [2]. En cuanto a la cuantificación de las resistencias, estas cuentan con un valor nominal que va desde algunos Ohmios hasta algunas decenas de mega-ohmios, también cuentan con una estabilidad que es el valor que se refiere a los posibles cambios que puede tener el valor óhmico de la resistencia con respecto al valor nominal debido, entre otras cosas, a los 1 que si por el contrario se trata de una pérdida o disminución, se habla de una caída de potencial. Para determinar la relación entre el voltaje y la corriente eléctrica, suponemos que tenemos un conductor de longitud l y sección transversal A tenemos que bajo la acción de un campo eléctrico la energía intercambiada por una carga dq en su movimiento a través de dicho conductor viene dada por: diferentes cambios de temperatura a los que están sometidas cuando presentan actividad eléctrica. En términos de electricidad el voltaje puede ser descrito como la presión que empuja las cargas a lo largo de un conductor, mientras que la resistencia eléctrica de un conductor es la medida en la cual existe cierta dificultad para empujar las cargas. Utilizando la analogía del flujo, la resistencia eléctrica es similar a la fricción, para el agua que fluye por un tubo largo y estrecho la resistencia será mayor a la que pasa por un tubo corto y ancho. En muchos materiales, la tensión y la resistencia están conectadas por la Ley de Ohm que relaciona la proporcionalidad entre voltaje, resistencia y corriente. V = IR La conexión entre el voltaje y la resistencia es más complicada en algunos materiales que se denominan no óhmicos. En la expresión anterior se asume que el campo eléctrico es constante en el interior del conductor. Tenemos también que la relación entre el campo eléctrico y la densidad de corriente es: Dado esto podemos calcular el voltaje como: Si se considera un conductor de área transversal A que conduce una corriente I. la densidad de corriente J en el conductor se define como la corriente por unidad de área. Puesto que la corriente I=nqvA, la densidad de corriente esta dad por: Y volvemos a deducir que la tensión entre los extremos del conductor es directamente proporcional a la corriente establecida, este factor de proporcionalidad se puede llamar también resistencia estática del conductor y también responde a la ley de ohm. [4]. Ahora para las resistencias que por sus características no responden a la ley de ohm por sus características térmicas, tenemos que para un intervalo limitado de temperatura, la resistividad de un compuesto cambia aproximadamente de forma lineal con la temperatura, de acuerdo a la expresión. A partir de esta ecuación se ve que la densidad de corriente está en dirección de del movimiento de la carga de los portadores de carga positiva y en dirección contraria de los portadores de cargas negativas. Una densidad de corriente J y un campo eléctrico E se establecen en un conductor cuando se mantiene una diferencia de potencial a través del conductor. Si esta diferencia de potencial se mantiene constante, la corriente también lo hará, y para los materiales denominados óhmicos la corriente será proporcional al campo eléctrico: Donde ρ es la resistividad a cierta temperatura T (en Cº), ρ₀ es la resistividad a una temperatura de referencia T₀, y α es el coeficiente de temperatura de resistividad. De acuerdo con la ecuación anterior se puede entonces expresar es coeficiente de temperatura de resistividad como: Donde la constante de proporcionalidad σ recibe el nombre de conductividad del conductor. Si un material obedece a esta ecuación se dice que cumple la ley de ohm [3]. Donde Δρ = ρ-ρ₀ es el cambio de resistividad en el intervalo de temperatura ΔT=T-T₀. Por lo tanto en este tipo de materiales la resistividad puede escribirse como: Por otra parte se tiene que el voltaje entre dos puntos de un conductor se puede definir como la energía que se intercambia por la unidad de carga al atravesar la distancia que separa dichos puntos: R = R₀ [1 – α (T - T₀)] El uso de esta propiedad permite hacer mediciones de temperatura precisas. [5] Si en dicho intercambio existe energía aportada desde el exterior, la tensión se denomina también fuerza electromotriz (fem), mientras 2 Las resistencias que responden al anterior modelo se denominan resistencias no óhmicas, el ejemplo más cotidiano es el bombillo. la diferencia de potencial con la intensidad en un punto concreto de operación, la dinámica relaciona los incrementos de ambas magnitudes en torno a un punto de operación (Q). [6] A partir de la ley de ohm se tiene entonces que: Conclusiones Dependiendo del tipo de compuesto, una resistencia podrá actuar dentro en un rango de temperatura. La elección del material depende fundamentalmente de la aplicación a que se destina. Una resistencia se denomina óhmica cuando ésta, en cierto rango de (T) mantiene una resistencia constante. En una resistencia óhmica, la gráfica de corriente vs. tensión es una recta y la pendiente de esa recta es el valor óhmico de la resistencia. Por lo general, las resistencias óhmicas operan dentro de un rango de temperatura bastante limitado. Y se sabe también que la resistividad es un parámetro que depende, en términos generales, del compuesto, de la temperatura y del campo eléctrico. Para el caso de conductores ideales o superconductores, la dependencia con el campo eléctrico es nula. Entonces se verifica la ley de Ohm, por la cual se plantea que la diferencia de potencial es directamente proporcional a la corriente que circula, con independencia de la corriente o el campo. Grafico 1 (Comportamiento de un material Óhmico). En aquellas resistencias que no son óhmicas, o no lineales, el coeficiente de (T) es bastante mayor, Por lo tanto la varía en cierto grado al variar la temperatura. Debido a que la temperatura de trabajo en estas resistencias es por lo general mucho más alta que la temperatura ambiente, su resistencia debe variar considerablemente con la temperatura. El valor óhmico de estas resistencias puede variar en un porcentaje considerable, sobre su valor a temperatura normal, cuando estas tienen su temperatura de trabajo, así mismo la gráfica de corriente vs. tensión, para estas resistencias es una curva, cuya pendiente, aumenta al incrementarse la corriente. Grafico 1 El comportamiento óhmico es característico de los materiales conductores como se demostró anteriormente. En cambio, como ya se había mencionado, existen otros materiales en los que la relación entre el voltaje y la intensidad tiene una dependencia en cuanto al punto de trabajo. Para estas situaciones, el valor de R no es constante, sino que es funcional en cada puto de trabajo específico. Grafico 2 (comportamiento de un material no-óhmico). Bibliografía [1] FLEURY, p. y MATHIEU, J.: Electrostática, corrientes continuas. Magnetismo. Ed. Paraninfo. Madrid. 1964 p. 6 a 9. [2] FLEURY, p. y MATHIEU, J.: Electrostática, corrientes continuas. Magnetismo. Ed. Paraninfo. Madrid. 1964 p. 170. [3] SERWAY, R. Física (Tomo II) (2000); 5ta. Edición; McGraw-Hill, México. [4] KANE, J.W. D; STERNHEIM, M. M. Física. 2º edición.Ed. Reverté. [5] SERWAY, R.; FAUGHN, J. (2001); 5ta. Edición; Pearson Educación, México. [6] Hemenway, Henry, Caulton, Física Electrónica. Editorial Limusa, 1992. Grafico 2[6] Para caracterizar a estos materiales se emplea un parámetro más que se denomina resistencia dinámica (r). Si la resistencia estática relaciona 3