Bloque 1

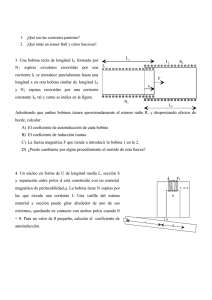
Bloque 1
Conceptos fundamentales de
los circuitos eléctricos
Teoría de Circuitos
1.1. Magnitudes básicas. Criterio de
signos. Lemas de Kirchhoff
Introducción
• Electromagnetismo: Estudia los
campos eléctricos y magnéticos y
su interacción
• Teoría de circuitos: Estudia las
relaciones entre corrientes y
tensiones de un circuito
Basadas en las
mismas
observaciones
experimentales
Circuito eléctrico
• Conjunto de elementos combinados de modo que se
pueda producir una corriente eléctrica
• Elementos activos: suministran energía eléctrica
• Elementos pasivos: consumen energía eléctrica
Excitación
CIRCUITO
ELÉCTRICO
(constante/variable)
Respuesta
Magnitudes básicas
•
•
•
•
Carga eléctrica
Corriente eléctrica
Tensión o diferencia de potencial
Potencia eléctrica
Carga eléctrica
•
•
•
•
•
•
Es la base para describir los fenómenos eléctricos
Propiedad de la materia presente en todos los cuerpos
Es de naturaleza bipolar (+ ó -)
El trasvase de carga entre unos cuerpos y otros es el origen de
cualquier fenómeno eléctrico.
Unidad SI: [C] qe=-1,6. 10-19C
El signo de las cargas es arbitrario, pero de él depende la
interacción entre ellas.
+
+
+
-
-
-
-
+
Corriente eléctrica
• Se produce por el desplazamiento de las cargas en
un material
dq
i=
dt
• Unidad SI [A]
Variación de carga por unidad de
tiempo en la sección transversal
de un conductor
Corriente eléctrica
CONVENIO DE SIGNO
Se considera que la corriente eléctrica es un
movimiento de cargas positivas
La conducción se debe a un desplazamiento de
electrones
-
-
Es equivalente suponer
un desplazamiento de
electrones en un
sentido
+
+
+
Que suponer un
desplazamiento de una
cantidad de carga +
equivalente en sentido
opuesto
Tensión o diferencia de
potencial
• Trabajo que se debe suministrar para mover una
carga entre dos puntos de un circuito
dw
u=
dq
[J ]
Unidad SI: [V ] =
[C ]
A
B
uA= potencial eléctrico en A
uB= potencial eléctrico en B
uAB= uA- uB = difencia de potencial entre A y B
uAB>0 A está a mayor potencial que B (al pasar de A a B las
cargas pierden energía)
uAB<0 A está a menor potencial que B (al pasar de A a B las
cargas ganan energía)
Tensión o diferencia de
potencial
SIMIL GRAVITATORIO
Ep=mgh
m
..... A
..... B
• Al pasar de A a B la masa pierde
energía potencial
• Al pasar de B a A la masa gana
energía potencial
Tensión o diferencia de
potencial
NOTACIÓN
• Punto de mayor potencial se denota +
• Punto de menor potencial se denota A
A
+
o bien
B
uAB>0
-
B
uAB>0
Potencia eléctrica
• Trabajo realizado por unidad de tiempo
dw
dq
p (t ) =
= u (t )
= u (t )i (t )
dt
dt
dw
u=
dq
• Unidades SI: [W]=[J]/[s]
Potencia eléctrica
CONVENIO DE SIGNO
A
+
dipolo
B
-
Dipolo absorbe potencia p>0 (ej. resistencia)
Dipolo cede potencia p<0 (ej. generador)
COHERENCIA DE LOS CRITERIOS DE SIGNOS DE U, I Y P
(p=ui)
A
+
dipolo i>0
B
A
uAB>0, i>0 =>p>0
Las cargas pierden
energía el dipolo la
consume
dipolo
+
i>0
B
uBA<0
I>0
p<0
Resumen convenio de signos
• Corriente:
– i>0 en el sentido del movimiento de las cargas +
• Tensión:
– uAB >0 A a mayor potencial que B
– uAB <0 A a menor potencial que B
• Potencia
– p>0 dipolo absorbe potencia
– p<0 dipolo cede potencia
i>0
i<0
A
A
uAB>0
B
uAB>0
B
Lemas de Kirchhoff
Definiciones topológicas
• Rama: Elemento que presenta dos terminales
• Nudo: Punto de confluencia de varias ramas
• Malla: Conjunto de ramas que forman un camino
cerrado y que no contienen ninguna otra línea
cerrada en su interior.
er
1
lema de Kirchhoff
La suma algebraica de las corrientes entrantes a un nudo
es nula en todo instante
Σ i(t) = 0
(Ley de conservación de la carga)
Ejemplo
i1
i1 + i2 − i3 + i4 − i5 = 0
i2
i3
i5
i4
Se consideran las
corrientes entrantes +
y las corrientes
salientes -
2º lema de Kirchhoff
La suma algebraica de las tensiones a lo largo de
cualquier línea cerrada en un circuito es nula en todo
instante.
Σ u(t) = 0
(Ley de conservación de la energía)
Ejemplo
+ u1
+
u5
q
u2
u4
+
+
+ u3
u1 − u 2 − u 3 + u 4 − u 5 = 0
Se consideran las
caídas de tensión + y
las elevaciones -
1.2. Elementos pasivos 1.
Resistencia
Elementos pasivos
Consumen o almacenan energía eléctrica
– Resistencias: disipan energía en
forma de calor
R
– Bobinas: almacenan y liberan energía
en forma de campo magnético
L
– Condensadores: almacenan y liberan
energía en forma de campo eléctrico
C
Elementos pasivos
• En general consideraremos:
– Elementos ideales
– Parámetros concentrados (=el efecto que se produce al
conectar una fuente se propaga instantáneamente)
– Conectados por conductores que no absorben potencia
(R=0, L=0, C=0)
Resistencia
• Elemento del circuito en el que se disipa potencia en
forma de calor
En general consideraremos resistencias ideales
Resistencia real
R
L
efecto resistivo + efecto inductivo
Resistencia ideal
R
se desprecia el efecto
inductivo
Resistividad
Material
Resistividad a 23°C
en ohmios - metro
Plata
1.59 × 10-8
Cobre
1.72 × 10-8
Oro
2.20 × 10-8
Aluminio
2.65 × 10-8
Tungsteno
5.6 × 10-8
Hierro
9.71 × 10-8
Acero
7.2 × 10-7
Platino
1.1 × 10-7
ρ= resistividad
Plomo
2.2 × 10-7
L=longitud del conductor
Nicromio
1.50 × 10-6
Carbón
3.5 × 10-5
Germanio
4.6 × 10-1
Silicio
6.40 × 102
Piel
humana
Vidrio
5.0 × 105 aproximadamente
Hule
1013 aproximadamente
Sulfuro
1015
• La resistencia que opone
un conductor al paso de
corriente depende de su
conductividad y de su
geometría
R=
l
l
=ρ
σS
S
ρ=
1
σ
S= sección del conductor
σ= conductividad
1010 to 1014
Fuente: Wikipedia
Resistencia
• La resistencia depende de la temperatura
R2 = R1 [1 + α (θ 2 − θ1 )]
α= coeficiente de variación
de resistencia con la
temperatura
Resistencia desde el punto de
vista del circuito
R
i
+
u
u = Ri
-
En la resistencia se produce una caída de
tensión. Las cargas pierden energía que se
disipa en forma de calor
Ley de Ohm
i
•Característica u/i de una resistencia
u
1
G=
R
conductancia
•Unidades en el SI:
[V ]
[Ω] =
[ A]
[1]
[S ] =
[Ω]
Potencia y energía
• Potencia disipada
2
u
p (t ) = u (t ) ⋅ i (t ) = R ⋅ i =
≥0
R
2
R
i
+
u
-
En una R la potencia se disipa en forma de calor
•Energía disipada
2
u
(τ )
2
w(t ) = ∫ Ri (τ )dτ = ∫
dτ ≥ 0
R
t0
t0
t
t
Asociación de resistencias en
serie
• Se dice que dos o más elementos están en serie si
por ellos circula la misma intensidad
i
u
+
R1
+ u - +
1
R2
u2 -
i
u
-
....
+
+
RN
uN -
i
Req
-
u = u1 + u2 + ... + un = iR1 + iR2 + ... + iRn = i ( R1 + R2 + ... + Rn ) = iReq
Req = R1 + R2 + ... + Rn
Divisor de tensión
• La tensión que cae en cada resistencia es una
porción de la tensión total
i
R1
u1
R2
RN
....
u2
uN
u
u k = Rk i = Rk
R
u
= k u
R1 + R2 + ... + R N Req
Asociación de resistencias en
paralelo
• Se dice que dos o más elementos están en paralelo si
están sometidos a la misma tensión
+
u
i1
i2
R1
R2
iN
...
RN
i
+
u
-
o bien
i = Geq u
1
1
1   1 
+ ⋅ ⋅ ⋅ ⋅ + u =
i = i1 + i2 + ... + iN =  +
u


Rn   Req 
 R1 R2
1
1
1
1
=
+
+ ..
Req R1 R2
Rn
G eq = G1 + G 2 + ... + G N
i
+
Req
u
-
Divisor de corriente
• Un divisor de corriente es una asociación de
resistencias en paralelo. La corriente que atraviesa
cada resistencia es una porción de la corriente total
i1 = uG1
u=
i
G1 + G2 + .... + Gn
i1 =
G1
i
G1 + G2 + .... + Gn
1
R
G
ik = k i = k i
1
Geq
Req
• Caso particular de dos resistencias en paralelo
i2
i
i1
R2
R1
R2
i1 =
i
R1 + R2
i2 =
R1
i
R1 + R2
Equivalencia estrella triángulo
Para que las dos configuraciones sean equivalentes, deben
proporcionar la misma respuesta ante la misma excitación=
debe presentar la misma resistencia vista desde cada par de
terminales
1
1
R1Y
R
R 3∆
R 3Y
3
2Y
2∆
R
•
2
3
R1∆
2
Resistencia entre cada par de
terminales
Resistencia entre 1 y 2:
(1)
R1Y
R 3Y
•
R3∆ ( R1∆ + R2 ∆ )
R1∆ + R2 ∆ + R3∆
Resistencia entre 2 y 3:
1
=
•
R1∆ ( R2 ∆ + R3∆ )
R1∆ + R2 ∆ + R3∆
(2)
1
Resistencia entre 3 y 1:
R2 ∆ ( R3∆ + R1∆ )
(3)
R
R
+
=
( 1∆ 3∆ )
R1∆ + R2 ∆ + R3∆
R
R2∆
=
R 3∆
2∆
3
3
R1∆
R1∆
2
1
R3∆
R3Y + R1Y = R2 ∆
2
2
3
R2Y + R3Y = R1∆ ( R2 ∆ + R3∆ ) =
R1Y
R2Y
2Y
R1Y + R2Y = R3∆ ( R1∆ + R2 ∆ ) =
1
R
•
2
Transformación triángulo estrella
•
Conocemos R1∆, R2∆ y R3∆ del una configuración en triángulo y
queremos calcular R1Y, R2Y y R3Y de la estrella equivalente
(1)+(3)-(2)
2 R1Y =
R3∆ ( R1∆ + R2 ∆ ) + R2 ∆ ( R3∆ + R1∆ ) − RA ( RB + RC )
2 R3∆ R2 ∆
=
R1∆ + R2 ∆ + R3∆
R1∆ + R2 ∆ + R3∆
R1∆ R2 ∆
R3∆ R2 ∆
R3∆ R1∆
R
=
R1Y =
(6)
(4) R2Y =
(5) 3Y
R1∆ + R2 ∆ + R3∆
R1∆ + R2 ∆ + R3∆
R1∆ + R2 ∆ + R3∆
Transformación estrella triángulo
•
Conocemos R1Y, R2Y y R3Y del una configuración en estrella y
queremos calcular R1∆, R2∆ y R3∆ del triángulo equivalente
Dividiendo 2 a 2 las relaciones anteriores (4), (5), (6)
R2Y R1∆
=
R1Y R2 ∆
R3Y R1∆
=
R1Y R3∆
R R + R2Y R3Y + R3Y R1Y
R1∆ = 1Y 2Y
R1Y
R3∆ =
R3Y R2 ∆
=
R2Y R3∆
Sustituyendo en (6) y
operando se llega a
R1Y R2Y + R2Y R3Y + R3Y R1Y
R2 ∆ =
R2Y
R1Y R2Y + R2Y R3Y + R3Y R1Y
R3Y
Resumen
RiY
Re sistencias _ conectadas _ nudoi∆
∏
=
∑R + R + R
1∆
Ri∆
2∆
3∆
Pr oductos _ binarios _ resistenciasY
∑
=
RiY
1.3. Elementos pasivos 2.
Condensadores y bobinas
Condensadores
Un condensador es un elemento pasivo capaz de
almacenar energía eléctrica
-
q
+ + + + + + + +
E
- - - - - - - -q
-
• Dos placas metálicas separadas
una distancia d y con un dieléctrico
entre ellas que impide un flujo de
carga
i
+
u
• Al aplicar una ddp entre ambas
placas aparece un trasvase de
carga entre ellas
• Se establece un campo eléctrico
en el que se almacena la energía
suministrada por la fuente
Capacidad
• La carga desplazada es proporcional a la tensión
aplicada
q = Cu
C = Capacidad
SI: [F]=Faradios
C
• La capacidad de un condensador depende de su
geometría
A
C = ε 0ε r
d
donde
ε 0 = 8,85
pF
m
Condensadores
R
• Los condensadores
reales suelen
presentar pérdidas
C
• Consideraremos
condensadores
ideales
C
Relación u/i
q = Cu => dq = C du
dt
dt
i (t )
=>
+
du
i (t ) = C
dt
i
u
-
C
• Si u=cte i=0 => En corriente continua un condensador se comporta
como un circuito abierto
t
t
t
du
1
∫t dt dt = C t∫ i(t )dt
0
0
=>
1
u (t ) − u (t0 ) = ∫ i (t )dt
C t0
• La tensión en un condensador no puede variar bruscamente
Potencia y energía
du
p (t ) = u (t )i (t ) = uC
dt
La potencia puede ser > ó < que 0 =>
el condensador absorbe o cede
potencia
•Energía almacenada entre 0 y t
t
t
du
1 2
W = ∫ p(t )dt = ∫ Cu
dt = Cu ≥ 0
dt
2
0
0
(Suponiendo que u(0)=0)
La energía almacenada es siempre mayor o igual que cero. Si el
condensador cede potencia lo hace a expensas de la energía
previamente almacenada => Es un elemento pasivo
Asociación de capacidades en
paralelo
i1
C1
+
i2
in
C.2 . .
Cn
u
i
i = i1 + i2 + .... + in
du
ik = Ck
dt
-
du
du
du
du
du
i = C1
+ C2
+ .... + Cn
= (C1 + C2 + ... + Cn ) = Ceq
dt
dt
dt
dt
dt
Ceq = C1 + C2 + .... + Cn
Asociación de capacidades en
serie
C1
+
C2
+ - + u1
u2
i
Cn
+
-
-
u = u1 + u2 + .... + un
un
u
duk
1
i
=
dt
Ck
dun 1
du du1 du2
1
1
i + ... +
i=
=
+
+ .... +
= i+
dt
dt
dt
dt C1
C2
Cn
 1
1
1 
=  +
+ ... + i = Ceq i
Cn 
 C1 C2
1
1
1
1
=
+
+ .... +
Ceq C1 C2
Cn
Bobinas
Una bobina es un dispositivo capaz de almacenar
energía magnética
Φ
• Al circular corriente por la bobina
aparece un flujo magnético
• Φ depende de la corriente
NΦ = Li
L=Coeficiente de autoinducción de la
bobina (o inductancia propia)
i
SI:[H]=Henrios
2
N 2 N S fe µ
=
L=
R
l fe
Relación u/i
• Si i que recorre la bobina es variable en el tiempo =>
Φ es variable => Se induce una f.e.m. que se opone
al flujo (Faraday Lenz)
+
di
dΦ
u = −e = N
=L
dt
dt
i
u
di
dΦ
N
=L
dt
dt
-
t
Si i=cte u=0 => En
corriente continua
una bobina se
comporta como un
cortocircuito
t
di
1
∫t dt dt = L t∫ u (t )dt
0
0
t
=>
1
i (t ) − i (t0 ) = ∫ u (t )dt
L t0
La corriente en una
bobina no puede
variar bruscamente
Bobinas
Una bobina es un dispositivo capaz de almacenar
energía magnética
Φ
• Al circular corriente por la bobina
aparece un flujo magnético
• Φ depende de la corriente
NΦ = Li
L=Coeficiente de autoinducción de la
bobina (o inductancia propia)
i
SI:[H]=Henrios
2
N 2 N S fe µ
=
L=
R
l fe
Relación u/i
• Si i que recorre la bobina es variable en el tiempo =>
Φ es variable => Se induce una f.e.m. que se opone
al flujo (Faraday Lenz)
+
di
dΦ
u = −e = N
=L
dt
dt
i
u
di
dΦ
N
=L
dt
dt
t
Si i=cte u=0 => En
corriente continua
una bobina se
comporta como un
cortocircuito
t
di
1
∫t dt dt = L t∫ u (t )dt
0
0
t
=>
1
i (t ) − i (t0 ) = ∫ u (t )dt
L t0
La corriente en una
bobina no puede
variar bruscamente
Potencia y energía
di
p (t ) = u (t )i (t ) = Li
dt
La potencia puede ser > ó < que 0 =>
la bobina absorbe o cede potencia
•Energía almacenada entre 0 y t
t
t
di 1 2
W = ∫ p (t )dt = ∫ Li = Li ≥ 0
dt 2
0
0
(Suponiendo que i(0)=0)
La energía almacenada es siempre mayor o igual que cero. Si la
bobina cede potencia lo hace a expensas de la energía previamente
almacenada => Es un elemento pasivo
Asociación de bobinas en
serie y en paralelo
u2
u1
i
....
u
uN
N
Leq = L1 + L2 + ...... + LN = ∑ Lk
k =1
i1
i2
iN
i
u
1
1 1
1
= + + ... +
Leq L1 L2
LN
Bobinas acopladas
• Un par de bobinas están acopladas entre sí, cuando
las tensiones en cada una de ellas dependen no sólo de
la corriente que circula por cada bobina sino también de
las corrientes que circulan por las demás bobinas
acopladas a ellas.
di1
di2
+M
u1 = L1
dt
dt
u 2 = L2
M=coeficiente de inducción mutua
(inductancia mutua)
di2
di
+M 1
dt
dt
SI: [H] =Henrios
Terminales correspondientes
•
Se dice que dos terminales de dos bobinas son
correspondientes entre sí si una corriente que entre por uno de
los terminales en la bobina 1 induce en la bobina 2 una tensión
del mismo sentido que la que induciría una corriente que
entrase por el terminal correspondiente de dicha bobina 2.
u1 (t ) = L1
di1 (t )
di (t )
+M 2
dt
dt
u2 (t ) = M
di1 (t )
di (t )
+ L2 2
dt
dt
Ejemplo: 3 bobinas acopladas
u1 (t ) = L1
di (t )
di1 (t )
di (t )
+ M 12 2 + M 13 3
dt
dt
dt
u3 (t ) = M 13
di (t )
di1 (t )
di (t )
− M 23 2 + L3 3
dt
dt
dt
u2 (t ) = −M12
di (t )
di1 (t )
di (t )
− L2 2 + M 23 3
dt
dt
dt
Potencia y energía
p(t ) = u1i1 + u2i2 = L1i1
di1 (t )
di (t ) 
di (t )
 di (t )
+ M 12 i1 2 + i2 1  + L2i2 2
dt
dt 
dt
 dt
w(t ) =
1
1
L1i12 + M 12 i1i 2 + L2 i 22 ≥ 0
2
2
Resumen elementos pasivos
• Resistencia
u (t ) = Ri(t )
i (t ) = Gu(t )
• Bobina
t
di (t )
u (t ) = L
dt
1
i = i (t0 ) + ∫ u (t )dt
L t0
• Condensador
t
1
u (t ) = u (t0 ) + ∫ i (t )dt
C t0
du (t )
i (t ) = C
dt
1.4. Elementos activos
Elementos activos
• Son los encargados de suministrar energía eléctrica
al circuito (fuentes o generadores)
•Ideales
•
Fuentes de tensión
•Reales
•Ideales
•
Fuentes de corriente
•Reales
•Independientes
•Dependientes
•Independientes
•Dependientes
•Independientes
•Dependientes
•Independientes
•Dependientes
Fuentes de tensión ideales
• Dispositivo que proporciona energía eléctrica con una
determinada tensión que es independiente de la
corriente que pasa por él
• El signo + se pone en el punto a
mayor potencial
+
+
o bien
ug
i
ug
i
•Si se conecta una carga al
generador de tensión ideal, éste
suministrará corriente al circuito.
i
• Característica u/i del dispositivo
ug
u
Potencia entregada por una
fuente de tensión ideal
La potencia eléctrica suministrada por el generador
de tensión será
ug
+
P
i
R
pg = u g i =
u g2
R
= u g2 G
La potencia
entregada a una R=0
(cortocircuito) es
infinita !!
R
Fuente de corriente ideal
• Dispositivo que proporciona energía con una
determinada corriente que es independiente de la
tensión en bornes
• La flecha indica el sentido de
circulación de la corriente
+
u
ig
-
•La tensión en bornes de la fuente
depende de la carga conectada a
ella (no tiene por qué ser 0!!!)
i
• Característica u/i
ig
u
Potencia entregada por una
fuente de corriente ideal
La potencia eléctrica suministrada por el generador
de corriente será
P
+
ig
R
u
-
p g = uig = Rig =
2
ig2
G
R->inf
R->0
G
Asociación de fuentes ideales
en serie
• Fuentes de tensión ideales en serie
u1
u2
ueq = u1 − u2 + ... + u N
+
...
+
+
+
• La corriente que circula por un conjunto de elementos en
serie es igual en todos ellos.
• Por tanto no es posible conectar en serie fuentes de
corriente de distintos valores en serie
un
N
ueq = ∑ u k
k =1
ueq
Asociación de fuentes ideales
en paralelo
• Fuentes ideales corrientes paralelo
– La tensión en un conjunto de elementos en paralelo es igual
en todos ellos.
– Por tanto no es posible conectar en paralelo fuentes de
tensión de distintos valores
i1
i2
...
in
ieq
N
ieq = i1 − i2 + ... + iN
ieq = ∑ ik
k =1
Fuente de tensión ideal en
paralelo con un elemento
• En lo que respecta a cálculos en el resto de la red
la presencia de un elemento en paralelo a la fuente
puede omitirse.
i1
+
i
+
ug
A
+
i
+
A
ug
R
i2
-
B
-
B
• Si se solicitan los valores internos i1 e i2 hay que
volver al circuito inicial.
Fuente de corriente ideal en
serie con un elemento
• En lo que respecta a cálculos en el resto de la red
la presencia de un elemento en serie con la fuente
puede omitirse.
R
+
+
ig
u2
A
+
-
A
+
+
ig
u
u1
u
-
•
B
-
B
Si se solicitan los valores de u1 y u2 hay que volver al circuito
inicial.
Fuentes dependientes
• La magnitud de la fuente dependiente está ligada a otra
magnitud de un elemento determinado del circuito
• Cuatro tipos de fuentes
+
ug=αu
circuito
+
u
-
F. TENSIÓN
controlada
por TENSIÓN
circuito
i
F. TENSIÓN
controlada
por CORRIENTE
+
ug=µi
circuito
+
u
ig=αu
circuito
i
-
F. CORRIENTE
controlada
por TENSIÓN
F. CORRIENTE
controlada
por CORRIENTE
ig=µi
Fuente de tensión real
• Elemento de un circuito que proporciona energía
eléctrica con una determinada tensión u(t) que
depende de la corriente que pasa por él
+
•Se representa mediante una
resistencia interna Rg de la fuente
i
+
ug
Rg
u
-
R
• Cuanto mayor sea la corriente que
atraviesa la fuente mayor será su
caída de tensión interna
u = e g − Rg i
Fuente de tensión real
• Curva u/i
u
eg
Circuito abierto (i=0)
Cortocircuito (u=0)
eg/Rg
i
Potencia entregada por una
fuente de tensión
• Al conectar R se genera una corriente
+
i=
i
+
ug
Rg
u
eg
u = Ri = R ⋅
Rg + R
R
p = ui = R ⋅
(R
eg
2
+ R)
2
g
eg
Rg + R
Parte de la potencia
entregada por la
fuente se consume en
su resistencia interna
pg = Rg ⋅
-
g
• Rendimiento de la fuente
η=
(R
eg
p
R
=
p + pg R + Rg
η →1
R→∞
2
+ R)
2
Transferencia de máxima
potencia
• La transferencia de potencia depende tanto de
Rg como de R
• La máxima transferencia se obtiene cuando
eg
2
dp
= 0 ⇒ R = Rg ⇒ Pmax =
dR
4R
P
Pmax
En este caso el rendimiento es del 50%
η=
R
= 50%
R + Rg
Rg
R
Fuente de corriente real
• Elemento que proporciona energía eléctrica con
una determinada i(t) que depende de la tensión en
bornes
• Curva u/i
i
+
ig
Rg
R
u
i
ig
Cortocircuito (u=0)
Circuito abierto (i=0)
-
i = i g − u / Rg
ig/Gg u
Potencia entregada por una
fuente de corriente real
• Al conectar una carga (resistencia R) , se genera una
corriente
i
+
i = ig −
ig
Rg
u
= ig − Gg u
Rg
u
p = ui = G ⋅
(G
ig
u=
2
+ G)
2
g
P
• Potencia máxima
Pmax
2
ig
dp
= 0 ⇒ G = Gg ⇒ Pmax =
dR
4Gg
Gg
R
ig − i
Gg
Fuentes reales equivalentes
•
Dos fuentes reales son equivalentes (de cara al resto de la red) si
para cualquier tensión aplicada suministran la misma corriente
i
i
+
+
Ri
ig
+
R
u
ug
Ru
u
-
-
i = ig − u / Ri
ig =
R
ug
Ru
y
Ru = Ri
u = u g − Ru i