31.- Calcular la flecha máxima y la σx máxima que resultan con el

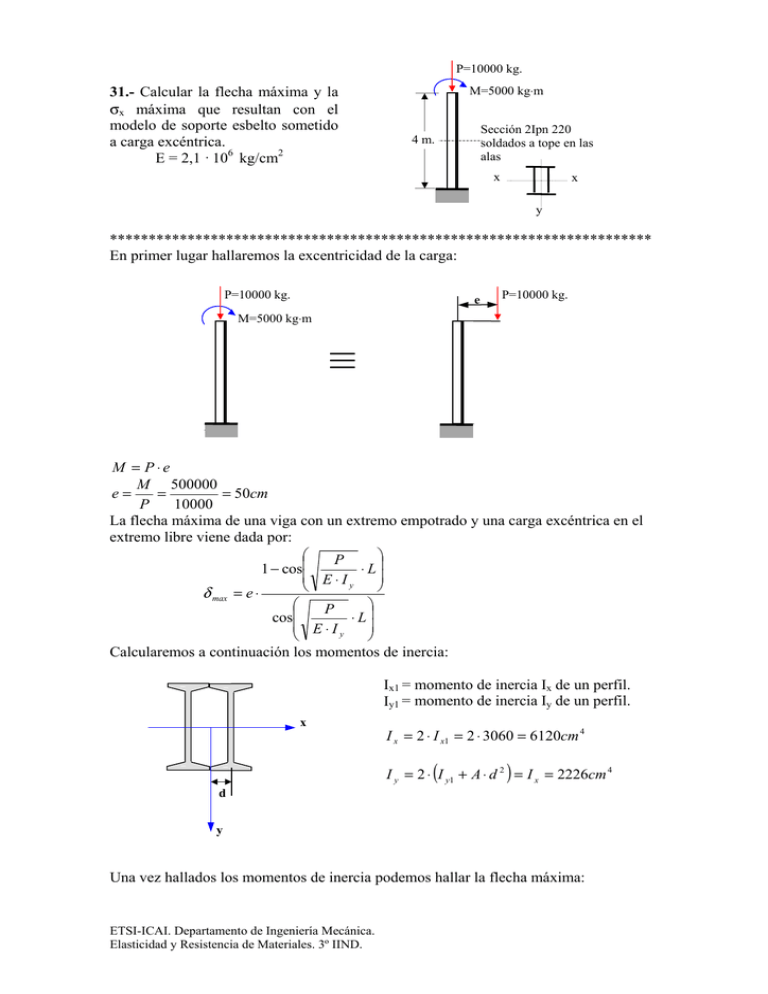
P=10000 kg.
31.- Calcular la flecha máxima y la
σx máxima que resultan con el
modelo de soporte esbelto sometido
a carga excéntrica.
E = 2,1 · 106 kg/cm2
M=5000 kg⋅m
Sección 2Ipn 220
soldados a tope en las
alas
4 m.
x
x
y
**********************************************************************
En primer lugar hallaremos la excentricidad de la carga:
P=10000 kg.
e
P=10000 kg.
M=5000 kg⋅m
M = P⋅e
M 500000
e=
=
= 50cm
P
10000
La flecha máxima de una viga con un extremo empotrado y una carga excéntrica en el
extremo libre viene dada por:
⎛
⎞
P
1 − cos⎜
⋅ L⎟
⎜ E⋅Iy
⎟
⎝
⎠
δ max = e ⋅
⎛
⎞
P
cos⎜
⋅ L⎟
⎜ E⋅Iy
⎟
⎝
⎠
Calcularemos a continuación los momentos de inercia:
Ix1 = momento de inercia Ix de un perfil.
Iy1 = momento de inercia Iy de un perfil.
x
I x = 2 ⋅ I x1 = 2 ⋅ 3060 = 6120cm 4
(
)
I y = 2 ⋅ I y1 + A ⋅ d 2 = I x = 2226cm 4
d
y
Una vez hallados los momentos de inercia podemos hallar la flecha máxima:
ETSI-ICAI. Departamento de Ingeniería Mecánica.
Elasticidad y Resistencia de Materiales. 3º IIND.
δ max
⎛
⎞
⎛
⎞
P
10000
⋅ L⎟
1 − cos⎜
⎜
⎟
−
⋅
400
1
cos
⎜ E⋅Iy
⎟
⎜ 2,1 ⋅ 10 6 ⋅ 2226
⎟
⎝
⎠ = 50 ⋅
⎝
⎠ = 9,97cm
= e⋅
⎛
⎞
⎛
⎞
10000
P
⋅ 400 ⎟⎟
cos⎜⎜
⋅ L⎟
cos⎜
6
⎜ E⋅Iy
⎟
⎝ 2,1 ⋅ 10 ⋅ 2226
⎠
⎝
⎠
b) La σx máxima se producirá en el empotramiento y será la
suma de la tensión provocada por la flexión más una compresión
uniforme.
σx =
My
Iy
⋅ x max +
P
A
donde x max = b siendo b el ancho del ala de un perfil.
x max = b = 4 ,9cm.
A = 79,2cm 2
M y = P ⋅ (e + δ max ) = 10000 ⋅ (50 + 9,97 ) = 599700kg ⋅ cm
Sustituyendo en la ecuación anterior obtenemos:
599700
10000
σx =
⋅ 4,9 +
= 1446 kg cm 2
2226
79,2
ETSI-ICAI. Departamento de Ingeniería Mecánica.
Elasticidad y Resistencia de Materiales. 3º IIND.
δmax
32.- ¿Cuál es la longitud de pandeo, en el plano de la figura, en los casos siguientes? En
todos los pórticos se supone el dintel infinitamente rígido. Supóngase que solo es
posible el pandeo en el plano de la figura.
a
2a
a
**********************************************************************
Debido a que la unión del dintel con los pilares es rígida, en todos los casos se debe
conservar el ángulo en la unión de éstos con el dintel.
En este caso no hay nada que impida el desplazamiento
lateral.
La deformada será:
La longitud de pandeo es la distancia entre dos inflexiones de la deformada (sinusoide).
lp = 2L
P
33.- Dimensionar la sección del pilar
biempotrado de la figura con el criterio:
N ⋅ω
1730 kg/cm2 ≥
A
Datos: P = 30000 kg
Acero A-42 E = 2,1·106 kg/cm2
Sección 2 Upn
Soldados en
cajón
6m
P
**********************************************************************
Debido a que el pilar es biempotrado, su longitud de pandeo lp es:
L
= 300cm.
2
Para determinar la dirección en la que pandeará necesitamos calcular el radio de giro
mínimo. Debemos proceder por tanteos; el esquema de cálculo es el siguiente:
lp =
Suponer
perfil
imin
λ
tablas
Supongamos UPN-180, los datos de un perfil son:
d
x
y
σ
ω
A1 = 28 cm2
Ix1 = 1350 cm4
Iy1 = 114 cm4
d = 5,08 cm
Para el conjunto de ambos perfiles:
I x = 2 ⋅ I x1 = 2700cm 4
(
)
I y conj = 2 ⋅ I y1 + A1 ⋅ d 2 = 1673,16cm 4
Al ser Iy < Ix pandeará de forma que la sección del pilar rote sobre el eje y; es decir: el
plano de pandeo es perpendicular a y.
El radio de giro mínimo será por tanto:
I y conj
imin = i y conj =
= 5,466cm
2 ⋅ A1
La esbeltez será:
lp
300
λ=
=
≈ 55
i y conj 5,466
Una vez hallado λ podemos obtener ω a partir de tablas: ω = 1,17
La tensión con dos UPN-180 en cajón es:
N ⋅ ω 30000 ⋅ 1,17
σ=
=
= 627 kg cm 2
2 ⋅ A1
2 ⋅ 28
Como la tensión es muy inferior a 1730 kg/cm2 podemos elegir un perfil menor.
Probaremos con UPN-120, los datos de un perfil son:
d
x
A1 = 17 cm2
Ix1 = 364 cm4
Iy1 = 43,2 cm4
d = 3,9 cm
Para el conjunto de ambos perfiles:
I x = 2 ⋅ I x1 = 728cm 4
(
y
)
I y conj = 2 ⋅ I y1 + A1 ⋅ d 2 = 603,5cm 4
Al ser Iy < Ix pandeará de forma que la sección del pilar rote sobre el eje y; es decir: el
plano de pandeo es perpendicular a y.
El radio de giro mínimo será por tanto:
I y conj
imin = i y conj =
= 4,213cm
2 ⋅ A1
La esbeltez será:
lp
300
λ=
=
≈ 71
i y conj 4,213
Una vez hallado λ podemos obtener ω a partir de tablas: ω = 1,36
La tensión con dos UPN-120 en cajón es:
N ⋅ ω 30000 ⋅ 1,36
σ=
=
= 1200 kg cm 2
2 ⋅ A1
2 ⋅ 17
Como la tensión es muy inferior a 1730 kg/cm2 podemos elegir un perfil menor.
Supongamos UPN-100, los datos de un perfil son:
A1 = 13,5 cm2
d
Ix1 = 206 cm4
Iy1 = 29,3 cm4
d = 3,45 cm
x
y
Para el conjunto de ambos perfiles:
I x = 2 ⋅ I x1 = 412cm 4
(
)
I y conj = 2 ⋅ I y1 + A1 ⋅ d 2 = 380cm 4
Al ser Iy < Ix pandeará de forma que la sección del pilar rote sobre el eje y; es decir: el
plano de pandeo es perpendicular a y.
El radio de giro mínimo será por tanto:
I y conj
imin = i y conj =
= 3,752cm
2 ⋅ A1
La esbeltez será:
lp
300
λ=
=
≈ 80
i y conj 3,752
Una vez hallado λ podemos obtener ω a partir de tablas: ω = 1,51
La tensión con dos UPN-100 en cajón es:
N ⋅ ω 30000 ⋅ 1,51
σ=
=
= 1678 kg cm 2
2 ⋅ A1
2 ⋅ 13,5
Como la tensión es ligeramente inferior a 1730 kg/cm2 elegimos:
UPN – 100
Los cálculos anteriores se pueden presentar en forma de cuadro para no tener que repetir
el razonamiento en cada iteración.
En el presente ejercicio los tanteos efectuados se pueden expresar mediante el siguiente
cuadro de cálculo.
UPN
180
120
100
b
7
5,5
5
c
1,92
1,60
1,55
A
28
17
13,5
Iy1
114
43,2
29,3
Iy conj
1673,2
603,5
380
iy conj
5,466
4,213
3,752
λ
55
71
80
ω
1,17
1,36
1,51
σ
627
1200
1678
En este caso el dintel no se puede desplazar
horizontalmente.
La deformada de la estructura será:
lp = 0,7L
En este caso no hay nada que impida el desplazamiento
lateral.
La deformada será:
La longitud de pandeo:
lp = L
Ambos pilares se encuentran biempotrados.
La deformada de la estructura será:
lp = L/2
a
2a
En los extremos del pilar está permitido el desplazamiento
lateral pero está impedido el desplazamiento vertical y el
giro.
La deformada de la estructura será:
a
lp = 2a
lp = 2a