fundamentos físicos de la ingeniería cuarta sesión de prácticas

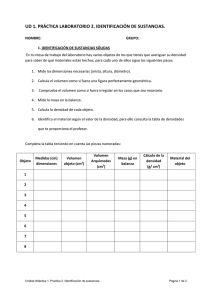
DEPARTAMENTO DE FÍSICA APLICADA
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS AGRÓNOMOS Y DE MONTES
UNIVERSIDAD DE CÓRDOBA
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA
CUARTA SESIÓN DE PRÁCTICAS
6.- Principio de Arquímedes. Aplicación a la
determinación de densidades de sólidos y líquidos
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA
Guión de prácticas
6.- Principio de Arquímedes. Aplicación a la
determinación de densidades de sólidos y líquidos
Objeto:
Verificar el principio de Arquímedes. Determinar la densidad de un
sólido mediante doble pesada. Determinar la densidad de un líquido
respecto a otro de referencia.
Material:
Balanza de 1 g de precisión. Dinamómetro. 2 vasos de precipitado
conteniendo uno agua destilada y el otro agua salina. 2 probetas de
0.5 l con los mismo líquidos. Densímetro. Un sólido cuya densidad
vamos a determinar.
Fundamento:
Principio de Arquímedes
Cuando un objeto sumergido se pesa
suspendiéndolo de un dinamómetro, la
lectura del dinamómetro (peso aparente) es
inferior al peso del objeto (Figura 6-1). Esto
se conoce como Principio de Arquímedes,
que puede enunciarse como:
Todo cuerpo parcial o totalmente
sumergido en un fluido experimenta
una fuerza ascensional igual al peso
del fluido desplazado.
El principio de Arquímedes
deducirse determinando el empuje
debido a la presión, que el fluido
sobre la superficie que delimita el
(Figura 6-2).
Figura 6-3
puede
total,
ejerce
sólido
Figura 6-1
El diagrama de cuerpo libre del sólido
sumergido se representa en la Figura 6-3, donde
P es el peso real del sólido, el medido con el
dinamómetro al aire; Pa es el peso aparente y E
el empuje. El equilibrio de fuerzas que existe nos
permite escribir:
Fy  0  Pa  E  P  0  E  P  Pa
6.1
Figura 6-2
(6.1)
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA
Guión de prácticas
El empuje del líquido
puede determinarse mediante
la doble pesada indicada en la
Figura 6-1.
Consideremos
ahora
un
recipiente con un líquido
sobre una balanza (Figura
6-4a). Si introducimos en él
un sólido (Figura 6-4b) la
lectura de la balanza aumenta
en una cantidad igual al peso
del líquido desalojado y por
lo tanto igual al empuje.
Figura 6-4
E   L2  L1  g
(6.2)
Densidad de sólidos
Como es bien sabido la densidad de un cuerpo, , es el cociente entre su masa y
el volumen que ocupa.

m
V
(6.3)
Cuando el sólido tiene una forma regular puede calcularse su volumen a partir de
las medidas de sus dimensiones, en caso contrario puede determinarse dicho volumen
utilizando el principio de Arquímedes.
Teniendo en cuenta el enunciado hecho anteriormente:
E
f
Vs g
(6.4)
siendo f la densidad del fluido, Vs el volumen del sólido y g la aceleración de la
gravedad.
Teniendo en cuenta también la expresión (6.1) el volumen del sólido será
P  Pa
E

fg
fg
Vs 
(6.5)
y la densidad:

P
P  Pa
6.2
f
(6.6)
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA
Guión de prácticas
Densidad de líquidos
La densidad relativa de un líquido puede determinarse utilizando el principio de
Arquímedes. Para ello no hay más que medir el peso aparente de un sólido cualquiera en
el líquido de referencia (generalmente agua destilada) y en el líquido problema.
El empuje en el líquido de referencia será:
E0 
Vg
(6.7)
Vs g
(6.8)
0 s
y en el líquido problema
E
Dividiendo (6.8) entre (6.7)
E

E0
Vs g
0Vs g


0
E
E0
(6.9)
Siendo la densidad del líquido:

0
E
E0
(6.10)
Densímetro
El densímetro es un sencillo aparato que se basa en el principio de Arquímedes y
sirve para medir densidades de líquidos. Consta de un bulbo de vidrio lastrado con
perdigones, que termina en un vástago con una escala previamente calibrada. Con el
lastre se asegura que el centro de gravedad del densímetro queda por debajo del centro
de cárena y por lo tanto se asegura la verticalidad del aparato cuando flota en un líquido.
El aparato se calibra marcando sobre la varilla
la posición de la superficie libre cuando flota en un
líquido de densidad conocida. El aparato se hundirá
una distancia h cuando se introduzca en un líquido
menos pesado y al contrario, emergerá al introducirlo
en un líquido menos denso.
Estableciendo el equilibrio del densímetro en
ambos líquidos puede deducirse la relación entre la
distancia entre las marcas de la escala y las densidades
de los líquidos.
h
0
Figura 6-5
Sea:
V0
el volumen sumergido del densímetro en el líquido de referencia
S
la sección externa del vástago
0
y
las densidades del líquido de referencia y el líquido problema,
respectivamente
Consideremos en primer lugar el densímetro en el líquido de referencia. El peso del
densímetro ha de ser igual al empuje del líquido:
mg
Vg
0 0
6.3
(6.11)
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA
Guión de prácticas
Considerando ahora el densímetro en el líquido problema:
mg
V0 hS g
(6.12)
Obteniéndose:
h
m 1
S
1
0
(6.13)
y por lo tanto

m
Sh
0
0
m
(6.14)
Método:
Determinación de la densidad de un sólido
(i)
Determinar la masa del sólido con la balanza y anotarla.
(ii)
Colgarlo del dinamómetro y observar como cambia la lectura en el mismo al
sumergir el sólido en un líquido.
(iii) Colocar sobre la balanza el vaso con agua destilada y poner a cero el aparato.
(iv) Introducir cuidadosamente el sólido en el líquido, sin que toque el fondo ni las
paredes, y anotar la lectura de la balanza.
(v)
Determinar la fuerza del empuje del agua destilada sobre el sólido.
(vi) Determinar la densidad del agua destilada a la temperatura del laboratorio
interpolando en la TABLA I
(vii) Calcular el volumen del sólido y su densidad.
Determinación de la densidad de un líquido
(viii) Repetir los pasos (iii) (iv) y (v) con el líquido problema (agua salina).
(ix) Determinar la densidad del líquido problema utilizando la ecuación (6.10) y el
valor de la densidad del agua destilada calculada en (vi).
(x)
Comprobar el resultado obtenido con el densímetro.
6.4
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA
Guión de prácticas
TABLA I
Densidad del agua destilada en función de la temperatura.
(g/cm3 )
T(º C)
T (º C)
(g/cm3 )
0
0,9998
45
0,9902
5
1,0000
50
0,9881
10
0,9997
55
0,9857
15
0,9991
60
0,9832
20
0,9982
65
0,9806
25
0,9970
70
0,9778
30
0,9956
75
0,9749
35
0,9941
80
0,9718
40
0,9922
TABLA II
Densidades de algunas sustancias
Sustancia
Agua
Aceite
Gasolina
Plomo
Acero
Mercurio
Madera
Aire
Butano
Dióxido de carbono
Densidad en kg/m3
1000
920
680
11300
7800
13600
900
1,3
2,6
1,8
6.5
Densidad en
g/c.c.
1
0,92
0,68
11,3
7,8
13,6
0,9
0,0013
0,026
0,018
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA
Guión de prácticas
Resultados:
Masa del sólido: m =
Lectura de la balanza con el sólido en agua destilada: L0 =
Fuerza de empuje en agua destilada: E0 =
Temperatura: t =
Densidad del agua destilada:
0
=
Volumen del sólido: V =
Densidad del sólido:
s
=
Lectura de la balanza con el sólido en el agua salina: L1 =
Fuerza de empuje en el agua salina: E1 =
Densidad del agua salina, Eq. (6.10):
1
=
Lectura del densímetro:
Cuestiones:
(1) ¿Qué indicaría la lectura de la balanza utilizada en la práctica si el sólido se deja
depositado sobre el fondo del vaso que contiene el agua?
(2) Un densímetro de 55 g de masa acaba en un tubo de 0.5 cm2 de sección. Si se
sumerge en agua el nivel del líquido alcanza la señal indicada con 1.00. Al sumergirlo
en otro líquido el densímetro se sumerge 1.5 cm. ¿Cuál es la densidad de este líquido?
(3) Un sólido está suspendido de un dinamómetro y tiene una masa de 150 g. Cuando se
introduce el sólido en agua destilada la lectura del dinamómetro es 120 g. Determinar el
volumen y la densidad del sólido en unidades del S.I.
6.6