Unidad 2.2
Anuncio
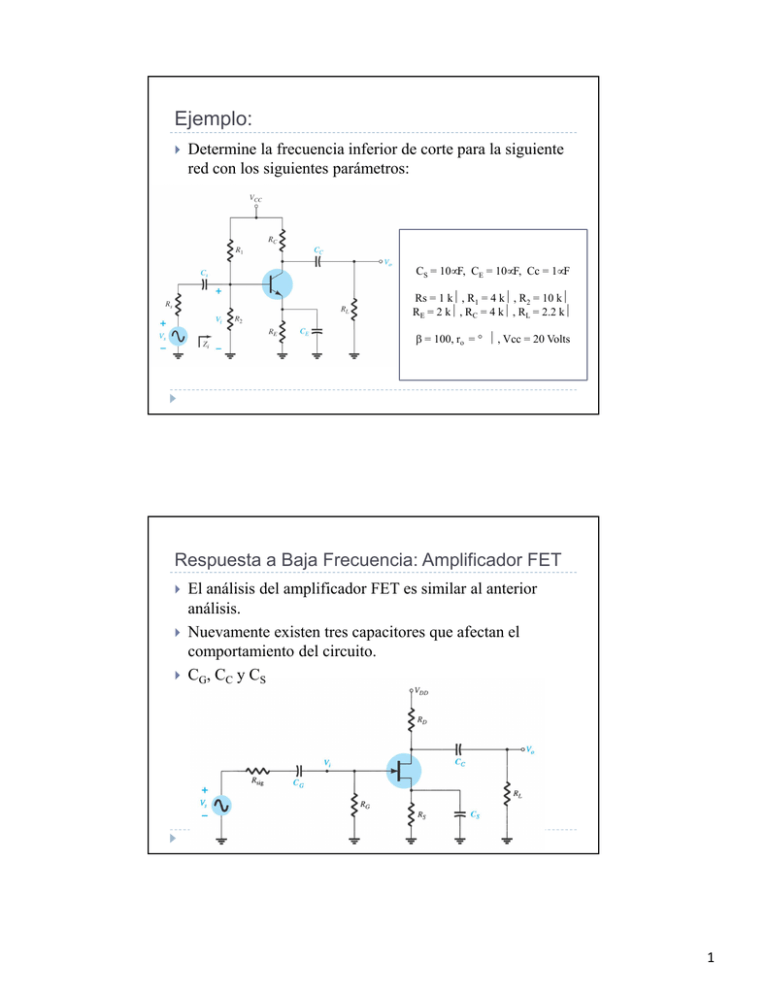
Ejemplo: Determine la frecuencia inferior de corte para la siguiente red con los siguientes parámetros: CS = 10µF, CE = 10µF, Cc = 1µF Rs = 1 kΩ, R1 = 4 kΩ, R2 = 10 kΩ RE = 2 kΩ, RC = 4 kΩ, RL = 2.2 kΩ β = 100, ro = ∞ Ω, Vcc = 20 Volts Respuesta a Baja Frecuencia: Amplificador FET El análisis del amplificador FET es similar al anterior análisis. Nuevamente existen tres capacitores que afectan el comportamiento del circuito. CG, CC y CS 1 El capacitor CG de acoplamiento entre la fuente y el transistor puede ser modelado como se indica en la siguiente red: f LG = 1 2π (Rsig + Ri )CG Se observa que Ri = RG . Es común tener una impedancia de entrada grande comparada con la resistencia de la fuente, lo cual RG y CG determinarían la frecuencia de corte. El capacitor CC de acoplamiento entre la carga y el transistor puede ser modelado como se indica en la siguiente red: 1 f LC = 2π (Ro + RL )CC Ro = RD || rd Para capacitor CS de la fuente la resistencia equivalente se 1 muestra como: f = LS 2πRecCS RS Rec = 1 + RS (1 + g m rd ) (rd + RD || RL ) Rec = RS || 1 gm rd ≅ ∞Ω 2 Ejemplo Determine la frecuencia inferior de corte para la red del siguiente circuito: CG = 0.01 µF, CC = 0.5 µF, Cs = 2µF Rseñal = 10 kΩ, RG = 1 MΩ, RD = 4.7 kΩ, RS = 1 kΩ, RL = 2.2 kΩ IDSS = 8 mA , Vp = -4 Volts, rd = ∞ Ω, VDD = 20 Volts Capacitancia de Efecto Miller Como veremos en la próxima sección, las capacitancias internas debido al dispositivo son las que resultan de suma importancia. Sin embargo para amplificadores inversores, la capacitancia de entrada y salida se ve afectada al nivel de la capacitancia internas del dispositivo, así como la ganancia del amplificador. Esta capacitancia esta definida como Cf 3 De la anterior figura se realiza el siguiente análisis: I i = I1 + I 2 Ii = Vi , Zi Vi Vi Vi (1 − Av ) = + Z i Ri XCf ⇒ I1 = Vi Ri I2 = Vi − V0 Vi − AvVi Vi (1 − Av ) = = XCf XCf XCf XCf 1 1 1 1 = + ⇒ = Z i Ri X C f (1 − Av ) 1 − Av ω (1 − Av )C f Donde el termino (1-Av)Cf resulta la capacitancia CM XCf 1 − Av = 1 = X CM ωCM ⇒ 1 1 1 = + Z i Ri X CM La impedancia de entrada esta constituida por una resistencia Ri y una capacitancia de retroalimentación que es multiplicada por la ganancia Cualquier capacitancia interna al dispositivo en la entrada del amplificador sera considerada en paralelo con Ri. Quedando definida la capacitancia de efecto Miller como: CM i = (1 − Av )C f De la figura de retroalimentacion nos damos cuenta que el efecto Miller incrementara la capacitancia de salida. 4 Un analisis similar se lleva acabo en la salida del amplificador I o = I1 + I 2 I1 = Vo , Ro I2 = Vo − Vi XCf Considerando Ro como una resistencia muy grande tendriamos Io = I2 Vi = Vo Av Io = XCf Vo − Vo Av I 1 − 1 Av Vo ⇒ o = ⇒ = XCf Vo XCf I o 1 − 1 Av Vo 1 1 = = I o ωC f (1 − 1 Av ) ωCM o ⇒ 1 CM o = 1 − C f ⇒ Av >> 1⇒ Av CM o = C f Respuesta a Alta Frecuencia: Amplificador BJT Los efectos de las capacitancias en alta frecuencia seran analizados. Los principales factores que afectan al amplificador son Capacitancias parasitas Capacitancias introducidas Además de la dependencia a la frecuencia de hfe(β). Para el análisis de alta frecuencia, la red RC será analizada. 5 Para frecuencias crecientes la reactancia Xc disminuye en magnitud, generando un efecto de corto circuito y una disminución en la ganancia. Av = 1 1 + j( f f2 ) Capacitancias parasitas debido a los materiales Capacitancias debido a los cables de conexión. Capacitancia Miller de entrada/salida CMi , CMo 6 Para el análisis en alta frecuencia los capacitores de acoplamiento y de bypassing serán considerados como corto circuitos, teniendo así el circuito equivalente siguiente: 7




