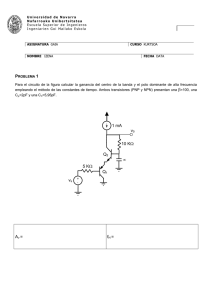
Av = 100 V/V fH = 4,88 MHz Q1 Q2 ∞ vs 5 KΩ 10 KΩ v0 1 mA
Anuncio

Universidad de Navarra Nafarroako Unibertsitatea Escuela Superior de Ingenieros Ingeniarien Goi Mailako Eskola ASIGNATURA GAIA CURSO KURTSOA NOMBRE IZENA FECHA DATA PROBLEMA 1 Para el circuito de la figura calcular la ganancia del centro de la banda y el polo dominante de alta frecuencia empleando el método de las constantes de tiempo. Ambos transistores (PNP y NPN) presentan una β =100, una Cµ=2pF y una Cπ=5,95pF. 1 mA v0 10 KΩ Q2 ∞ 5 KΩ Q1 vs Av = 100 V/V + - fH = 4,88 MHz SOLUCIÓN i b1 VS RS rπ 1 C µ1 B1 + vπ1 - E1 Cπ 1 E2 β ⋅ i b1 ib 2 rπ 2 β ⋅ i b2 Cπ 2 C2 V0 Rc C µ2 RS VS C µ1 rπ 1 + vπ1 - Cπ 1 g m 2 vπ 2 rπ 2 g m1 vπ 1 + vπ 2 - ⋅⋅⋅ Cπ 2 1 gm2 Ganancia en el centro de la banda β + 1i vs = Rs + rπ 1 + rπ 2 // 1 b1 g m 2 i b1 = vs R s + rπ 1 + (rπ 2 // 1 g m2 )(β + 1) (β + 1) ⋅ i vπ 2 = rπ 2 // 1 b1 g m 2 Rc C µ2 v0 = Rc g m 2 vπ 2 (β + 1) Rcg m 2 rπ 2 // 1 g m 2 v0 ∆v = = = 100V V vs (β + 1) R s + rπ 1 + rπ 2 // 1 g m2 rπ 1 = rπ 2 = 2500Ω οC µ 1 Rs = 5000Ω (β + 1) ≅ 2500Ω Rµ 1 = R s // rπ 1 + rπ 2 // 1 g m 2 οCπ 1 β = 100 g m 2 = 0,04 1 + Rs g m ≅ 1253Ω Rπ 1 = rπ 1 // 2 g m οCπ 2 Rπ 2 = rπ 2 // 1 g m2 //(rπ 1 + Rs ) // rπ 1 + Rs g m rπ 1 οC µ 2 Rµ 2 = Rc = 10000Ω f p1 = 1 1 = 4,88MHz 2π C µ1 R µ1 + Cπ 1 Rπ 1 + C µ 2 Rµ 2 + Cπ 2 Rπ 2