EFECTO DOPPLER v

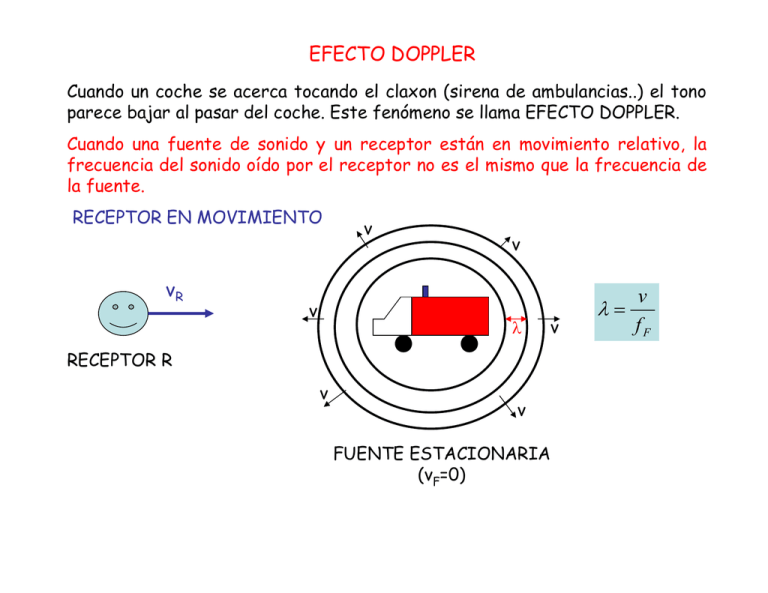
EFECTO DOPPLER
Cuando un coche se acerca tocando el claxon (sirena de ambulancias..) el tono
parece bajar al pasar del coche. Este fenómeno se llama EFECTO DOPPLER.
Cuando una fuente de sonido y un receptor están en movimiento relativo, la
frecuencia del sonido oído por el receptor no es el mismo que la frecuencia de
la fuente.
RECEPTOR EN MOVIMIENTO
vR
v
v
v
λ
v
RECEPTOR R
v
v
FUENTE ESTACIONARIA
(vF=0)
λ=
v
fF
La fuente emite una onda sonora con frecuencia fF y longitud de onda λ=v/fF.
Las crestas de onda se acercan al receptor con rapidez de propagación relativa
al receptor de v+vR. La frecuencia con que llegan al receptor es:
fR =
v + vR
λ
v + vR  v + vR 
 vR 
=
=
 f F = 1 +  f F
v / fF  v 
v 

Un receptor que se mueva hacia la fuente (vR > 0) oye una frecuencia más
alta (tono más agudo) que un receptor estacionario.
Un receptor que se aleja de la fuente (vR < 0) oye una frecuencia más baja
(tono más grave) que un receptor estacionario.
FUENTE EN MOVIMIENTO Y RECEPTOR EN MOVIMIENTO
v
v
vR
vF
v
λ
λ
v
RECEPTOR R
v
v
FUENTE EN MOVIMIENTO
Si la fuente también se mueve con velocidad vF, la rapidez de la onda
relativa al medio (aire) sigue siendo v, pero la longitud de onda no es igual a
v/fF. El tiempo que tarda en emitirse un ciclo de la onda es el periodo
T=1/fF. Durante este tiempo, la onda viaja una distancia vT=v/fF y la fuente
se mueve de una distancia vFT=vF/fF. La longitud de onda depende del
desplazamiento relativo entre la fuente y la onda, es diferente adelante y
atrás de la onda.
v
vR
v
vF
v
λ
λ
v
RECEPTOR R
v
v
FUENTE EN MOVIMIENTO
La longitud de onda adelante de la fuente es:
λ=
v vF v − vF
−
=
fF fF
fF
En la región a la izquierda de la fuente:
λ=
v vF v + vF
+
=
fF fF
fF
fR =
v + vR
λ
v + vR
=
(v + v F ) / f F
v + vR
fR =
fF
v + vF
Fuente móvil, receptor móvil
EJEMPLO 16.16 Una sirena policiaca emite una onda senoidal con frecuencia
fF=300 Hz. La rapidez del sonido es de 340 m/s. a) Calcule la longitud de
onda del sonido si la sirena está en reposo en aire. b) Si la sirena se mueve a
30 m/s (108 km/h), calcule λ para las ondas adelante y atrás de la fuente.
a) Cuando la fuente está en reposo:
λ=
v 340m / s
=
= 1.13m
fF
300 Hz
b) Delante de la sirena:
λ=
v − vF (340 − 30)m / s
=
= 1.03m
fF
300 Hz
Detrás de la sirena:
λ=
v + vF (340 + 30)m / s
=
= 1.23m
fF
300 Hz
EJEMPLO 16.18 Si la sirena está en reposo y el receptor se mueve hacia la
izquierda a 30 m/s, ¿qué frecuencia oye?
v
vR
v
λ
v
RECEPTOR R
v
v
FUENTE ESTACIONARIA
(vF=0)
La dirección positiva es del receptor hacia la fuente:
fR =
v + vR
(340 + (−30)m / s
(300 Hz ) = 274 Hz
fF =
v
340m / s
EJEMPLO 16.19 Si la sirena se está alejando del receptor con una rapidez de
45 m/s relativa al aire, y el receptor se mueve hacia la sirena con una rapidez
de 15 m/s relativa al aire, ¿qué frecuencia oye el receptor?.
v + vR
(340 + 15)m / s
fR =
fF =
(300 Hz ) = 277 Hz
v + vF
(340 + 45)m / s
EJEMPLO 16.20 La patrulla con su sirena de 300 Hz se mueve hacia una
bodega a 30 m/s, intentando atravesar su puerta. ¿Qué frecuencia escucha
el conductor reflejada de la bodega?
En este caso, hay dos cambios Doppler. En el primero, la bodega es
el “receptor” estacionario. La frecuencia del sonido que llega a la
bodega, fB, es mayor que 300 Hz porque la fuente se acerca. En el
segundo, la bodega actúa como fuente de un sonido con frecuencia
fB y el receptor es el conductor de la patrulla, quien oye una
frecuencia mayor que fB porque se acerca a la fuente.
fB =
v
340m / s
fF =
(300 Hz ) = 329 Hz
v + vF
(340 + (−30)m / s
v + vR
(340 + 30)m / s
(329 Hz ) = 358Hz
fR =
fB =
v
340m / s
16.38 En el planeta Arrakis, un ornitoide macho vuela hacia su compañera a 25
m/s mientras canta a una frecuencia de 1200 Hz. La hembra estacionaria oye
un tono de 1240 Hz. Calcule la rapidez del sonido en la atmósfera de Arrakis.
El receptor no se mueve, vR=0:
v + vR
v
fR =
fF =
fF
v + vF
v + vF
f R (v + vF ) = vf F
v( f R − f F ) + f R vF = 0
Fuente hacia la izquierda
vF < 0
− f R vF − (1240 Hz )(−25m / s )
v=
=
= 775m / s
fR − fF
(1240 − 1200) Hz
16.42 Al nadar, un pato patalea una vez cada 1.6 s produciendo ondas
superficiales con ese periodo. El pato avanza con rapidez constante en un
estanque en el que la rapidez de las ondas superficiales es de 0.32 m/s, y las
crestas de las olas adelante del pato están espaciadas de 0.12 m. a) Calcule la
rapidez del pato. b) ¿Qué tan separadas están las crestas detrás del pato?
λ
a)
0.12m
vF = v − = 0.32m / s −
= 0.25m / s
1.6s
T
b)
λ=
v + vF (0.32 + 0.25)m / s
=
= 0.91m
fF
1 /(1.6 s)
El tracto vocal humano es un tubo que se extiende unos 17 cm de los labios a
los pliegues vocales (también llamados “cuerdas vocales”). La garganta se
comportan como un tubo cerrado. Estime las primeras tres frecuencias de
onda estacionaria del tracto vocal, con v=344 m/s.
FORMULARIO – SEGUNDO PARCIAL
Péndulo de torsión:
MAS
x = A cos(ωt + ϕ )
T = 2π
v = dx / dt = −ωA sin(ωt + ϕ )
a = dv / dt = −ω 2 A cos(ωt + ϕ )
Disco:
1 2 1 2 1 2
kA = kx + mv
2
2
2
T = 2π
L
g
Péndulo físico:
T = 2π
I0
Mgd
v=
Momentos de inercia:
Energía MAS
Péndulo simple:
I0
k
Anillo:
1
MR 2
2
MR
2
Teorema de ejes paralelos:
I = I cm + Md 2
y = A cos(kx + ωt )
2π
λ
; ω = 2πf =
ω = kv; v = λf
τ
m
; µ = ;τ tensión
µ
L
Ondas sonoras:
y = A cos(kx − ωt )
p = BkA cos(kx − ωt )
pmax = BkA; B = v 2 ρ
2
pmax
1
I=
Bρ ω 2 A2
=
2 ρv 2
I
β = 10dB log ;
I0
I 0 = 10 −12W / m 2
Ondas en cuerdas:
k=
Rapidez en una cuerda
Ondas estacionarias
2π
T
y = 2 A sin( kx) sin(ωt )
Modos normales en una cuerda:
fn =
nv
n τ
=
2L 2L µ
λ=
2L
n
n = 1,2,3..
Modos normales en un tubo:
Tubo abierto:
Tubo cerrado:
2L
n
n
fn =
v n = 1,2,3..
2L
λ=
4L
2n − 1
n
fn =
v n = 1,2,3..
4L
λ=