Cap. 16: Superposición y ondas estacionarias
Anuncio

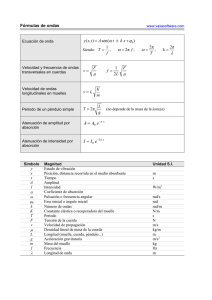
Cap. 16: Superposición y ondas estacionarias Principio de Superposición: Cuando dos o más ondas se combinan, la onda resultante es la suma algebraica de las ondas individuales. Este principio es consecuencia de la linearidad de la ecuación de onda: ∂ y 1 ∂ y = 2 2 2 v ∂t ∂x 2 2 Interferencia de ondas armónicas y1 = A sin ( kx − ω t ) , y2 = A sin ( kx − ω t + φ ) y = y1 + y2 = A sin ( kx − ω t ) + A sin ( kx − ω t + φ ) ⎛ ⎞ ⎛ ⎞ y = A sin ⎜ kx − ω t ⎟ + A sin ⎜ kx − ω t + φ ⎟ ⎜ ⎟ ⎜ ⎟ α ⎝ ⎠ ⎝ β ⎠ Usando la siguiente identidad ⎛α − β sin α + sin β = 2 cos ⎜ ⎝ 2 ⎞ ⎛α + β ⎞ ⎟ sin ⎜ ⎟ ⎠ ⎝ 2 ⎠ tenemos: φ⎞ ⎛ φ⎞ ⎛ y = ⎜ 2 A cos ⎟ sin ⎜ kx − ω t + ⎟ 2⎠ ⎝ 2⎠ ⎝ La onda resultante es otra onda armónica de igual número de onda y frecuencia. La amplitud de la onda resultante es 2Acos(φ/2) y la constante de fase es φ/2. Si φ = 0, entonces la amplitud es 2A y la interferencia es constructiva. Si φ = π, entonces la amplitud es cero y la interferencia es destructiva. Ver ejemplo 16.6. Ondas estacionarias Considera una cuerda atada a ambos extremos (ejemplo: cuerda de guitarra). Las ondas viajando a la izquierda interfieren con las que viajan a la derecha y para ciertas frecuencias, forman el patrón de onda estacionaria ilustrado en la figura. y1 ( x, t ) = A sin ( kx − ωt ) y2 ( x, t ) = A sin ( kx + ωt ) y = y1 + y2 = A sin (kx − ωt ) + A sin (kx + ωt ) Usando 1 1 sin α + sin β = 2 cos (α − β) sin (α + β) 2 2 tenemos y = [2A sin kx ] cos ωt Vemos que la ecuación predice que existe un nodo en x = 0, lo cual es correcto. Vemos que en x = L hay otro nodo, por lo tanto sin kL = 0 ∴ kL = n π 2π 2L L = n π ∴ λn = λ n v n = fn = v λn 2L n T fn = 2L µ Ejemplo: Una cuerda se estira entre dos soportes fijos distantes 0.70 m entre sí y se ajustan hasta que la frecuencia fundamental de la cuerda es 440 Hz. Calcula la velocidad de las ondas transversales en la cuerda. Ejemplo: Una cuerda de 3 m de longitud, y densidad lineal 0.0025 kg/m, está sujeta por ambos extremos. Una de las frecuencias de resonancia es 252 Hz. La siguiente frecuencia de resonancia es 336 Hz. ¿Qué armónico corresponde a los 252 Hz? Calcula la frecuencia fundamental y la tensión en la cuerda.