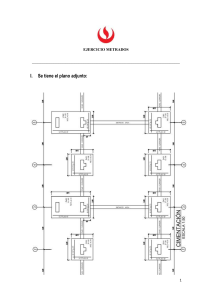
zapatas aisladas
Anuncio

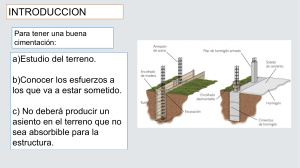
ZAPATAS AISLADAS • Económicas < de 30% del área • Profundidad mínima • Reemplazo • Trabajo independiente • Vulnerable a asentamientos diferenciales ENSANCHAMIENTO DE COLUMNAS ZAPATAS COMBINADAS ISE EN ZAPATAS Asentamiento Uniforme = Reacción no Uniforme METODO “RIGIDO” Cimentación Rígida Ks = q/δ q PONER EL DOBLE DE ACERO ! Carga admisible igual para todas las zapatas P q = 2 ⇒B= a B P qa B 1.4B P 2P 2B 4P 4p P B 2B δ L 2L PL q a L δ= = EA E P q = cte δ = cte 1 B VIGAS DE FUNDACION VIGAS DE FUNDACION Funciones Secundarias Funciones Principales • Control asentamientos diferenciales • Disminución de esbeltez de columnas • Estabilidad solicitaciones horizontales • Arriostramiento en laderas • Zapatas medianeras • Atención excentricidades no consideradas CONTROL DE ASENTAMIENTOS DIFERENCIALES Las Vigas de fundación disminuyen los asentamientos diferenciales ? Cimentación bien diseñada Asentamientos con V F 30x30 (mm) B Sin estructura Con estructura sin V F Con estructura V F no apoyada δ δ m δ 1.6 ∆ 77 14 74 ∆ δ 12 73 ∆ 51 61 60 57 20 2.3 ∆ Con estructura V F apoyada 11 62 Cimentación mal diseñada Asentamientos con V F apoyada Sección cm Sin 30x30 ∆ mm 29 22 ∆ /L 1/227 1/303 30x60 15 1/455 30x90 9 1/746 ESTABILIDAD SOLICITACIONES HORIZONTALES • Mayor dimensión ≥ L /20 para DES L /30 para DMO L /40 para DMI • Tensión ó compresión = 0.25 Aa Pumax • Refuerzo longitudinal continuo • Refuerzo transversal a h/2 ó 30 cms REVISION DE RESISTENCIA Tensión φPn = 0.9 Fy As Compresión φPn = 0.8 φ ( 0.85 f’c Ac) φ= 0.7 Asmin = 0.01 Ac Si las vigas reciben momentos deben cumplir con requisitos para vigas DES, DMO y DMI ATENCION EXCENTRICIDADES NO CONSIDERADAS • La misteriosa desaparición del momento P ? • Diseñar zapata a flexión biaxial P Mu ARRIOSTRAMIENTO EN LADERAS PARA Cimentaciones para Geotecnistas ir a Cimentaciones Especiales DISEÑO DE ZAPATAS AISLADAS CONCENTRICAS 1. Calcular lado: B = Ps qa P de servicio sin zapata ni lleno qa = 1.33 qa si P es con W ó E. 2. Mayorar: Pu = F.C. x P (F.C= 1.5 para cargas verticales normales) 3. Suponer d> 150mm +70 en suelo 40 en lleno hmin = 220mm 4. Cortante Bidireccional (punzonamiento) ν ubd ν ubd Pu (B2 - (b1 + d) (b2 + d)) = 2 B 2 (b1 + d + b2 + d) d αs = 40 columna interior zapata 30 columna en el borde 20 columna en la esquina φ < φ φ f' c 3 f' c αs d (1 + ) 6 2 bo f' c 2 (1 + ) 6 βc βc = b1/ b2 b0 = Perímetro b1 > b 2 5. Cortante Unidireccional (acción de viga) B b B b1 B - 1 - d - d 2 2 = PU 2 2 Bd d B2 ν uud = PU B2 ν uud φ f' c < 6 b1 < b2 Con: φ = 0.85 6. Calcule momento y hierro 2 Pu B B b1 Pu B b1 Mu = 2 - - = 2B 2 2 B 2 2 2 Asmin= 0.0018 B d 2 7. Revisar el aplastamiento Es más importante con columnas de acero PEDESTALES Pasar 4 Barras As min=0.005Ac Ld a compresión a ambos lados • Aumentar recubrimiento • Mejorar anclaje de hierro de vigas de fundación Ejemplo: placa 50 x 50 sobre pedestal 60 x 60 DISEÑO DE ZAPATAS AISLADAS CON FLEXION UNIAXIAL Si e < L / 6 qmax = P 6eP P 6e + = 1 + 2 BL B L BL L 6e P 6eP P qmin = − = (1 ) 2 BL B L BL L Si e > L / 6 3 qmB P= 2 1.- DIMENSIONAMIENTO. L> 6e 6e P B= (1 + ) qa L L≈B ó 2.- Mayorar ≈ 3.- Punzonamiento L ≈ 1 .5 ó 2 B Pu < φ fc / 3 b0d 4. Cortante Unidireccional vud = Vu <φ Bd fc / 6 5.- Acero largo, Mu 6.- Acero corto > 0.0018 Ld casi siempre EJEMPLO ZAPATA UNIAXIAL Valla Publicitaria Patología de Vallas por viento ZAPATAS CON FLEXION BIAXIAL (Caso General) ex = ey = My P Mx P ≤ L/6 ≤ B/6 6 ex 6 ey P q= ( 1± ± ) < qa BL L B ≥0 REVISAR LOS MISMOS CONCEPTOS QUE EN LOS OTROS CASOS