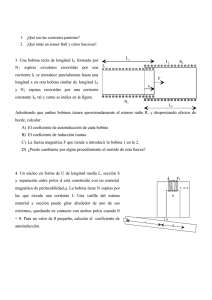
Apuntes de Física IV - CECyT No. 1

INSTITUTO POLITÉCNICO NACIONAL
Centro De Estudios Científicos Y Tecnológicos No. 1
“GONZALO VÁZQUEZ VELA”
APUNTES DE FÍSICA
IV
(Basados en RAP´s)
PROF. EDUARDO ALFARO MIRANDA
1
P R O L O G O
Los presentes APUNTES DE FÍSICA IV , están diseñados de acuerdo a los objetivos
previamente establecidos en el Programa de estudios de la asignatura Física IV, que
se imparte en el sexto semestre en los Centros de Estudios Científicos y Tecnológicos
de Área Ciencias Físico -Matemáticas pertenecientes al INSTITUTO POLITÉCNICO
NACIONAL y tienen el objetivo de apoyar al estudiante como un material de auto
estudio.
Estos apuntes no intentan ser los únicos materiales de consulta; el alumno deberá
realizar esfuerzos por ampliar sus conocimientos de la materia consultando otras
bibliografías escritas y de carácter electrónico.
Construyendo fundamentalmente el principio básico de la educación en el nuevo
modelo educativo que contiene, con un esfuerzo que intenta inducir hacia la búsqueda
de otros conocimientos, y no pretenden se totalizador en el sentido de que los
alumnos puedan considerar que todos los conocimientos tienen una relación con la
asignatura y otras ciencias.
Deseo agradecer a la Academia de FÍS ICA T.V. su valiosa colaboración, disposició n,
contribución, sugerencias y mejoras en la elaboración de estos apuntes.
“La Técnica al Servicio de la Patria”
Ing. Eduardo Alfaro Miranda
2
Í N D I C E
D E
L A
U N I D A D
F Í S I C A
D E
A P R E N D I Z A J E
I V
TEMAS
PÁG.
6
ELECTROMAGNETISMO
G e nera lid ad e s
I ma ne s
T eo rías d el ma g ne ti s mo
Fl uj o ma g n ét ico
Mat eria le s ma g n é tico s
13
Fuerzas entre masas magnéticas
Le y d e Co u lo mb p ar a e l ma g n et i s mo
Co mp ar ac ió n d e f u er za s
Campos magnéticos generados por corriente eléctrica
21
Exp eri me n to s d e Oer s te d
Le y c irc ui ta l d e A mp e r e
Le y d e B io t - Sa v ar t
Ind uc ció n ma g né ti ca d e u na b o b i na
Ex ci tac ió n ma g n ét ica
P er meab i lid ad ma g n ét ic a
P er meab i lid ad ma g n ét ic a d e u n se le no id e
Ind uc ció n Ma g n éti ca d e u n to r o id e
C ur va d e ma g n et iza ció n
Ci clo d e hi s tér e s is
40
Fuerzas magnéticas
F uerz a s so b r e u na car g a en mo vi mi e n to
F uerz a d e Lo r e n tz
F uerz a so b r e u n al a mb r e co n co r r ie nt e
F uerz a e n tr e ala mb r e s p ar al elo s
54
Instrumentos de medición
Gal v a nó me tr o
A mp er í me tr o
Vo l tí me tr o
Inducción electromagnética
65
Le y d e I nd u cció n d e Far ad a y
Le y d e Le nz
Fe m d e mo vi mie n to
El ge n erad o r
Valo r e s má x i mo , me d io y e f ic az
El tr a n s fo r mad o r
86
Inductancia
Ge ner al id ad e s
Cá lc u lo d e la i nd uc ta nc i a
En er gía al mac e nad a e n u na b o b i na
98
El circuito magnético y la Ley de Ohm
La Le y d e O h m d e l ma g ne ti s mo
Co mp ar ac ió n d e lo s c ir c ui to s e léc tri co y ma g n ét ico
3
ONDAS
Movimiento ondulatorio
108
O nd a s
O nd a s tr a ns v er sal e s y o nd a s lo n gi t ud i n ale s
Acústica
117
So nid o
Car act erí s tic a s d e l so n id o
Velo cid ad d el so n id o
Efecto Do p p ler
ÓPTICA
La luz y sus características
137
Ge ner al id ad e s
Velo cid ad d e la l uz
Re fle x ió n, r e f r ac ció n y d isp er s ió n d e la l uz
157
Espejos
Ge ner al id ad e s
Esp ej o có n ca vo
Esp ej o co n v e xo
Esp ej o p l a no
175
Lentes
Ge ner al id ad e s
Le nte s co n ver ge n te s
Le nte s d i ver g e nte s
199
Instrumentos ópticos
Oj o h u ma n o
Cá ma ra fo to gr á f ic a
Fi ltro ó p ti co
207
FÍSICA MODERNA
4
COMPETENCIA GENERAL
ESTA ASIGNATURA TIENE COMO OBJETIVO PRINCIPAL
QUE LOS ALUMNOS DESARROLLEN SU CAPACIDAD
CREATIVA Y AUTODIDACTIVA PARA LA SOLUCION DE
PROBLEMAS FISICOS MEDIANTE LA TEORIA Y
EXPERIMENTACION, PROPICIANDO EN EL ALUMNO EL
PROCESO DE CONSTRUCCION DEL CONOCIMIENTO DE
TAL MANERA QUE SEA SIGNIFICATIVO, EN DONDE EL
PROFESOR COMO MEDIADOR DEL CONOCIMIENTO
CONDUZCA
A
REALIZAR
ACTIVIDADES
EXPERIMENTALES EN EQUIPOS COLABORATIVOS QUE
LES PERMITAN DESARROLLAR HABILIDADES DE
OBSERVACION, REFLECCION Y ANALISIS DE LOS
FENOMENOS FISICOS, QUE FORMAN PARTE DE SU VIDA
DIARIA
COMO
SON:
MAGNETISMO,
ELECTROMAGNETISMO, MOVIMIENTO ONDULATORIO Y
FISICA MODERNA.
5
COMPETENCIA PARTICULAR 1.
Construir los conceptos, principio y leyes fundam entales del electrom agnetism o,
explicando y procediendo los fenóm enos de carga eléctrica en m ovim iento com o
generadora del cam po m agnético así com o sus interacciones con los cam pos eléctricos y
m agnéticos, de tal manera que aplique estos conocim ientos en el área tecnológica y su
vida cotidiana.
RESULTADO DE APRENDIZAJE PROPUESTO (RA P) No.1
Inducir m ediante investigación docum ental y experiencias recreativas, al estudio del
m agnetism o y sus propiedades.
UNIDAD # 1 DEL PROGRAMA: ELECTROMAGNETISMO
Generalidades
 Consideraciones preliminares
Etimologías. La palabra magnetismo se origina en una región del Asia menor
llamada Magnesia, donde fueron encontrados en la antigüedad unos trozos de mineral
que poseen la propiedad de atraer fragmentos del mismo material. A este material se
le llamó magnetis-litus, que significa piedra de magnesia (o piedra imán) y que hasta
nosotros ha llegado con el nombre de magnetita.
Debido a esta propiedad que posee la magnetita, se le llama magnética, y todos
los materiales que tienen o pueden adquirir las propiedades de la ma gnetita se dice
que son magnéticos.
Manifestación del magnetismo. El magnetismo, en general, se pone de
manifiesto a través de fuerzas de acción a distancia llamadas fuerzas magnéticas .
Estas fuerzas son interacciones entre imanes, y más generalmente puede n
considerarse como interacciones entre partículas cargadas en movimiento.
Necesidades del estudio del magnetismo. Podemos decir que el magnetismo es
la parte de la Física que estudia los fenómenos magnéticos para determinar sus causas
y establecer las leyes que los rigen.
El conocimiento del magnetismo al ser integrado a la tecnología podrá aplicarse
en beneficio del hombre, de ahí la necesidad de su estudio.
Concepto de magnetostática. La magnetostática es la parte de la Física donde
los fenómenos magnéti cos no están explícitamente relacionados con corrientes
eléctricas, la magnetostática estudia.

Los imanes y sus interacciones.

Las propiedades del campo magnético, sin analizar su origen , y el
efecto que éste produce sobre los cuerpos magnéticos o sobre cargas en
movimiento.
La parte del magnetismo donde intervienen corrientes eléctricas recibe el
nombre de electromagnetismo.
6

Imanes
Concepto de imán. Un imán es un objeto capaz de ejercer
fuerzas de acción a distancia sobre algunos metales o sobre objetos
similares a él.
Clasificación de los imanes. Los imanes se clasifican en dos
clases: Naturales y artificiales. Los naturales son los que están
formados por óxidos de materiales ferromagnéticos como las ferritas
y la magnetita. Los imanes artificia les pueden ser de dos tipos:
Permanentes y electroimanes. Un imán permanente puede se una pieza
de acero o aleación de metales ferromagnéticos que por frotamiento o
electrificación adquieren propiedades magnéticas permanentes.
Un electroimán está formado p or una bobina con un núcleo de hierro dulce. En
este dispositivo solo aparece campo magnético cuando circula corriente por la bobina
y desaparece al suspender la corriente.

 FERRITAS
 NATURALES 

MAGNETITA
IMANES 
 ARTIFICIAL ES  PERMANENTE S

 ELECTROIMÁN
Formas de imanes . De acuerdo a las necesidades y requerimientos de su uso,
los imanes (generalmente artificiales) se construyen de diferentes formas y de
acuerdo a su forma, es como suele llamárseles. Así, por ejemplo, tenemos: Imán
barra; Imán de herradura; Imán esférico ; Imán de bolas e Imán de aguja.
Imán de herradura
Imán de barras
7
Imán de bolas
Imán de aguja
Imán esférico
Fig. 1
Ecuador y polos de un imán. Cuando un imán de aguja se suspende por su
centro de gravedad, al detenerse apunta sensiblemente en la dirección norte –sur
geométricos, es decir, en la dirección de los polos, por tal motivo, a los extremos de
un imán se l es llamó polos. Al que apunta hacia el norte, se le llamó polo norte del
imán, y al que apunta hacia el sur como polo sur del imán. A la parte media del imán
se le llama ecuador magnético.
N
S
El espectro magnético de un imán pone de
manifiesto que el campo magnético es muy intenso
en los polos y muy débil en el ecuador.
N
N
S
S
Concepto de dipolo magnético. Cuando un
imán de barra se parte, en vez de aparecer un polo
norte y un polo sur separados, aparecen con su
respectivo polo norte y sur.
S
N S
N
Fig. 2
Si el proceso se repite muchas veces, el resultado, invariablemente será el
mismo: Siempre aparecerá un imán con dos polos. Al parecer no es posible aislar un
solo polo magnético, ya que incluso las partículas subatómicas presentan
características de dipolo magnético, aunque en a lgunos experimentos se puede
simular que se tiene un solo polo magnético con la ayuda de un imán de bolas.
Ley de los polos. Experimentalmente se ha demostrado que cuando dos imanes
se aproximan por sus polos del mismo nombre, éstos se rechazan, pero sí se
aproximan por polos de diferente nombre, se atraerán, con esto concluimos que:
Polos del mismo nombre se rechazan y
Polos de nombre diferente se atraen.
8

Teorías del magnetismo
Teoría del magnetismo de Weber. Wilhelm Weber, físico alemán (1804 -1891),
expuso su teoría según la cual todos los materiales están formados por imanes
moleculares (o contienen imanes moleculares) distribuidos por el interior de la
sustancia sin ningún orden y que en estas condiciones el material no presenta ninguna
propiedad magnética.
Pero sí por algún método estos imanes moleculares se orientan todos en el
mismo sentido, los campos generados por cada imán se suman y, entonces, el material
presentará propiedades magnéticas.
Fig. 3
En la Fig . 3 se presentan imanes moleculares desordenados y alineados.
Teoría del magnetismo de Ampere. Andrés María Ampere, físico francés
(1775-1836), propuso la teoría de que las propiedades m agnéticas de un cuerpo
proceden de una multitud de diminutas corrientes cerradas que se encuentran en el
interior del mismo: estas corrientes debían circular indefinidamente como si no
hubiera resistencia.
En un cuerpo no imantado, estos circuitos están or ientados al azar, y sí por un
proceso magnetizante, estos circuitos se alinean de modo que sus planos queden
paralelos entre sí y con las corrientes circulando en el mismo sentido, el cuerpo
presentará, entonces, propiedades magnéticas.
b 
a 
c 
Fig. 4
En la Fig . 4 , si las corrientes eléctricas son colocadas (mediante proceso
externo) en planos paralelos entre sí y todas circulando en el mismo sentido a  se
cancelan todas las del interior, excepto las de las orillas, lo que conforma un circuit o
b  , el cual es equivalente a un arrollamiento magnetizante c  .
9
Magnetismo terrestre. Descripción del campo magnético de la Tierra.
Cuando un imán de barra se suspende, oscila por la acción del campo magnético
terrestre debido a un par magnético.
Después de algunas oscilaciones termina por orientarse en la dirección norte sur, entonces el polo del imán al norte se llama polo norte y el polo del imán que
apunta al sur se llama polo sur.
De lo antes expuesto y debido a la ley
concluye que al polo norte geográfico de la
magnético, y al polo sur geográfico, un polo
comporta como si tuviera en su interior un imán
sur hacia el norte.
que rige a los polos magnéticos se
Tierra le corresponde un polo sur
norte magnético; Así, la tierra se
con polo n orte hacia el sur y su polo
Posibles causas del magnetismo terrestre. El globo terrestre envuelve bajo su
corteza un núcleo central cuyo estado de agregación no se conoce aún, en el que
domina la presencia de sustancias metálicas, princ ipalmente el hierro que puede
imantarse fácilmente si se somete a los efectos de un campo magnetizante.
El Sol posee una carga electrostática cuyo movimiento de rotación determina
un campo magnético perpendicular al plano de rotación. Así, el campo magnético
solar existe y el núcleo terrestre, buen conductor de la electricidad, e mueve con
velocidad constante dentro del campo magnético.
No es, pues, sorprendente que nuestro mundo manifieste el carácter de un
cuerpo magnetizado que actúa como el indu cido de una máquina dinamoeléctrica
recorrida por corrientes que modifican y perturban nuestro propio magnetismo y
causan, por ejemplo, las tempestades
magnéticas.
Concepto de ángulo de inclinación.
Cuando un imán se orienta, su posición no es
paralela a la superficie de la Tierra, sino que
forma un ángulo  que recibe el nombre de
ángulo de inclinación. En el ecuador
magnético, el ángulo de inclinación es 0 º , la
aguja es paralela a la horizontal.
En los polos magnéticos de la Tierra,
los imanes se orientan perpendicularmente a
la superficie, el ángulo de inclinación es de
90 º .
Polo
magnético
Polo geográfico

Linea isóclina
Fig. 5
10
La Tierra se comporta como si tuviera en su interior una barra de imán
inclinada con respecto al eje terrestre, debido a esta razón, la posición de los polos
magnéticos de la tierra no coinciden con la posición de los polos geográficos de la
misma. Esto da logar a que un imán orientado con los polos magnéticos tienda a
formar un ángulo  con el meridiano, que recibe el nombre de ángulo de inclinación.
De la Fig . 5 se deduce que la declinación de la aguja en el lugar “ A ” no es la
misma que en “ B ” y, ésta a su vez, distinta de la que tiene en “ C ”, es decir, que l a
declinación varía como es natural, según el lugar de la Tierra que se considere.
Concepto de líneas isóclinas. A cada lugar de la Tierra corresponde en un
momento dado una inclinación, de manera que al lugar geométrico de todos los
puntos sobre la Tierra que tiene el mismo ángulo de inclinación reciben el nombre de
líneas isóclinas.
Concepto de líneas isógonas. En forma similar
a lo anterior, a cada lugar de la Tierra corresponde un
momento dado un ángulo de inclinación, así, al lugar
geométrico de todos los puntos sobre la Tierra que
tienen el mismo ángulo de inclinación se llaman
líneas isógonas.
Concepto de campo magnético. Definiremos el
campo magnético como la región del espacio donde
existen fuerzas de carácter magnético.

Línea
isógona
Fig. 6
Sabemos que un punto del espacio pertenece a un campo magnético si sobre una
carga de prueba que se mueve por la región, actúa una fuerza magnética. Si se
dispone de una aguja de acero como un pequeño imán de prueba, al colocarla en un
punto del campo magnético actuará sobre muestra una fuerza magnética.
Concepto de inducción magnética. La inducción magnética se representa con
la letra “ B ” y es la cantidad física que nos sirve fundamentalmente para describirle
campo magnético. En el S. I. su unidad es el tesla, siendo:
tesla 
weber
wb
 2
2
metro m
Características de la inducción magnética “ B ”. La inducción magnética es
una cantidad vectorial porque tiene magnitud, dirección y sentido, características que
se le confieren en virtud de que puede describirse en función de fuerzas magnéticas,
las cuales por ser vectoriales también poseen magnitud, dirección y sen tido. Para
referirnos a la inducción magnética como vector usaremos el símbolo “ B ”, y el
símbolo “ B ” nos indicará solo su magnitud.
11
Líneas de inducción. Tales líneas son imaginarias y nos
sirven para representar gráficamente el campo magnético. En un
imán, se dibujan saliendo del polo norte y entrando al polo sur.
El número de líneas de inducción que salen del polo nortee debe
ser igual al número de líneas que entran al
polo sur en virtud de que el cam po
magnético es continuo. La tangente a una
línea de inducción en un punto dado nos da
la dirección del campo magnético en ese
punto.
Las líneas de inducción nunca se cruzan, si se
cruzarán, el campo magnético tendría dos direcciones
en un mismo punto, y esto es imposible. El número de
líneas de inducción por unidad de área se sección
transversal es proporcional a la intensidad del campo magnético.
A
B
C
12
B
B
B
RESULTADO DE APRENDIZAJE PROP UESTO (RAP) No.2
Aplicar las leyes de Coulom b y Gauss del m agnetism o y los modelos m atem áticos en la
solución de problem as .

Flujo magnético
Concepto de flujo magnético. El flujo magnético se representa con la letra
“  ”, y algunas veces, para diferenciarlo del flujo eléctrico se escribe “  B ”. Éste
representa el número de líneas de inducción que atraviesan normalmente una
superficie y se define como el producto escalar:
1
  B A
1
Siendo A el vector normal a la superficie. La ecuación asociada a la ecuación
es:
  B A cos 
2
Donde “  ” es el ángulo entre A y B .
“ A ” es el valor del área interpretada como la
magnitud del vector A .
A

El flujo magnético definido por la
ecuación 1 solo es válido cuando la
superficie en cuestión es plana, en caso
contrario, se deben considerar elementos
diferenciales de superficie y elementos
diferenciales de flujo.
B
C
d  B  d s
Para conocer el flujo total se debe integrar sobre la superficie.
   d   B  d s
3
Resumiendo de las ecuaciones 1, 2 y 3 , tenemos:
 : Flujo magnético.
B : Es la inducción magnética.
B : Es la magnitud del vector B .
A : Es el vector normal a la superficie.
A : Es la magnitud del vector A (lo que mide la superficie).
 : Es el ángulo entre
A y B . d : Es un elemento diferencial de fluj o
magnético.
13
Características del flujo magnético. Éste es una cantidad escalar porque se
define como un producto escalar. Si B y d s son colineales y del mismo sentido, d
es positivo, y si B y d s son colineales y de sentidos opuestos, d será negativo, ya
que cos 0 º  1 y cos 180 º  1 .
La transformación de la ecuación
según sea la forma de la superficie.
3
a la forma escalar varía en cada caso
Unidades del flujo magnético. Como en el S. I., la unidad de “ B ” es
wb
, y las
m2
unidades del área son m 2 , la unidad del flujo magnético es el weber, “ wb ”:
weber 
weber
2
 metro  wb
2
metro
Concepto de densidad de flujo magnético. Como   B  A , entonces B 

, así
A
vemos que la inducción magnética se puede expresar como el flujo por unidad de
área, debido a eso algunas veces se le llama densidad de flujo magnético .
Ley de Gauss del magnetismo. Nuestro objetivo es deducir una ecuación
conocida como Ley de Gauss del magnetismo. Consideremos un imán en el interior de
una esfera de radio “ R ”, el flujo magnético para esta superficie es:
  Bd s
El símbolo

indica que la integral se hace sobre toda la superfici e de l a
esfera. El número de líneas de inducción que salen de la esfera es igual al número de
líneas que entran, por lo tanto, el número neto de líneas de inducción que atraviesan
a la superficie de la esfera es cero y entonces:
  Bd s  0
El cual es conocido como la Ley de Gauss del magnetismo, el cual nos conduce
a dos conclusiones:
a)
El flujo magnético para una superficie cerrada es cero.
b)
No existen polos magnéticos aislados.
14

Materiales magnéticos
Clasificación de los materiales magnéticos. Tales materiales se clasifican en
tres grupos:
Diamagnéticos
Paramagnéticos
Ferromagnéticos
Propiedades de los materiales ferromagnéticos. Los materiales ferromagnéticos
son atraídos fuertemente en presencia de un imán. La permeabilidad relativa de
dichos materiales es cientos, y aún miles, de veces mayor que la unidad. Cuando una
muestra de estos materiales es colocada cerca del polo magnético de un imán, los
dipolos magnéticos de la muestra alcanzan un alto grado de alineamiento a pesar de
las vibraciones térmicas, y por lo ta nto, la magnetización es muy grande, así la cara
de la muestra más cercana al imán se comporta como un polo de nombre contrario y
es fuertemente atraída hacia el imán.
N
S
S
Muestra
Imán
Propiedades de los materiales paramagnéticos. Estos materiales son atraídos
débilmente en presencia de un imán. La permeabilidad relativa de dichos materiales
es ligeramente mayor a la unidad. Cuando una muestra de estos materiales es
colocada cerca del polo magnéti co de un imán, el alineamiento que alcanzan los
dipolos magnéticos de la muestra es sensiblemente contrarestado por los choques
entre los átomos si la muestra es un gas o por las vibraciones térmicas si es un sólido,
y por lo tanto, la magnetización es mu y pequeña, así, la ara de la muestra más
cercana al imán se comporta como un polo de nombre contrario y es atraída hacia el
imán aunque débilmente.
N
S
S
Muestra
Imán
Propiedades de los materiales diam agnéticos. Estos materiales son repelidos
ante la presencia de un imán, por lo cual su permeabilidad relativa es menor que la
unidad. Cuando una muestra de un material de estas características se coloca cerca
del polo magnético de un imán, el alineamiento de los dipolos magnéticos de la
muestra, además de des muy débil, ocurre en sentido contrario al de los materiales
ferromagnéticos, y por lo tanto, la magnetización es muy pequeña y aparece en
sentido contrario al campo del imán, así la cara de la muestra más cercana al imán se
comporta como un polo del mismo nombre y es repelido por éste, aunque muy
débilmente.
N
S
N
Muestra
Imán
15
Fuerzas entre masas magnéticas
Concepto de masa magnética. La masa magnética se representa con la letra
“ m ”. Como el campo magnético de un imán se pone de manifiesto básicamente en los
polos, se pensó que el asiento del campo magnético estaba precisamente en los polos
y que esta propiedad se debía a l a sustancia de que estaban hechos los polos del imán
y a la cual se le llamó masa magnética . Sin embargo, al parecer el magnetismo de un
imán se debe al alineamiento de las corrientes electrónicas (como lo postula la teoría
del magnetismo de Ampere), de mo do que la masa magnética ciertamente no existe,
siendo en realidad un artificio matemático que nos permite manejar con facilidad las
interacciones entre polos magnéticos.
Unidades de la masa magnética. En el S. I. su unidad es el ampere-metro o
weber,  A m o wb, el cual se define como la masa magnética que colocada frente a
otra igual a 1 m de distancia se repele con una fuerza de 10 7 N

Ley de Coulomb para el m agnetismo
Conceptos preliminares. El físico francés Charles Augustin de Coulomb
(1736-1806) estudió las interacciones entre polos magnéticos, estableciendo la ley
que lleva su nombre. En los experimentos de electrostática, Coulomb usó una balanza
de torsión para establecer dicha ley utilizando peque ñas esferas cargadas que se
comportaron como cargas puntuales. La dificultad en el magnetismo es que no existen
polos magnéticos aislados y la interacción del polo contrario en el extremo del imán
dificultaba los experimentos. Coulomb resolvió este problem a utilizando un imán de
bolas lo más largo posible, simulando, así, que tenía un polo magnéticos aislado.
Ley de Coulomb para el magnetismo. La fuerza de atracción o de repulsión
entre dos polos magnéticos es directamente proporcional al producto de sus ma sas
magnéticas, e inversamente proporcional al cuadrado de la distancia que los separa.
F  m1 m 2
F
1
r2
Estas dos proposiciones se pueden escribir en una sola:
F
Introduciendo una constante
proporcionalidad anterior en una
proporcionalidad.
m1 m 2
r2
de proporcionalidad, convertimos a
igualdad. Elegimos como constante
o
4
16
la
de
Por lo tanto, la expresión matemática de la Ley de Coulomb del magnetismo se
puede escribir como.
F
 o m1 m 2
4 r 2
1
Donde:
F : Es la fuerza de atracción o de repulsión ente polos magnéticos.
m 1 m 2 : Son las masas magnéticas.
r : Es la distancia entre las masas magnéticas.
 o : Es la constante de permeabilidad del aire o vacío y tiene el valor:
 o  4   107
wb
A m
Ejemplos.
1.
Dos masas magnéticas están separadas 4 cm y se rechazan con una fuerza de
10 3 N , si m 1  2 A  m , ¿cuánto vale m 2 ?
Datos :
r  4 cm  4  102 m
 o m1 m 2
F
4 r 2
F  103 N
m1  2 A  m
Fórmulas :
2
4  r 2 F 4  4  10  2 m  103 N 
 m2 

 o m1
4   107 Awbm  2 A  m
m2  8 A  m
17
2.
Dos masas magnéticas, tales que una es el doble de la otra se rechazan con una
fuerza de 5 10 2 N cuando están separadas 4 cm . Calcular el valor de las masas
magnéticas.
Datos :
F  5  102 N
m 1  2m 2
F
 o m1 m 2  o m1 2m1   o 2m1


4 r 2
4
r2
4 r 2
r  4 cm
Fórmula :
2
 m1 
m1  20 A  m
4 r 2 F

2o
4  4  10  2 m  5  10  2 N 
2 4   10 7 Awbm 
2
m 2  40 A  m
Ejercicios.
1.
Dos polos de igual masa magnética se rechazan con una fuerza de 10 3 N cuando
están separadas 20 cm . Calcular la fuerza con que se rechazan cuando están separadas
40 cm .
2.
Dos masas magnéticas, tales que una es el triple de la otra, se rechazan con una
fuerza de 6.5 10 4 N cuando están separadas 6 cm . Calcular el valor de las masas
magnéticas.
18
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No 3
Interpretar las características de las líneas de fuerza de cam pos m agnéticos uniform e y no
uniform e y los m odelos m atem áticos correspondientes en la solución de problem as de
flujo m agnético.

Comparación de fuerzas
Inducción magnética de un polo magnético. Sean un polo magnético, cuya
masa magnética es m ' , a una distancia r de un polo magnético cuya masa magnétic a
es m . De acuerdo con la Ley de Coulomb, la fuerza que la masa m ' ejerce sobre la
masa m está dada por la ecuación:
 o m'
m
F  
2 
4

r


 A
La inducción magnética producida por m ' en el punto donde está m se puede
definir como la fuerza magnética por unidad de polo magnético, o sea:
B
B 
F
m
Sustituyendo F de  A en B  , tenemos.
  o m'   1 
m  
B  
2 
 4 r   m 
B
o m'
4 r2
1
Donde:
B : Es la inducción magnética producida por un polo magnético cuya masa
magnética es m ' .
r:
Es la distancia que hay de m ' al punto donde se evalúa B .
 o : Es la constante de permeabilidad  o  4  10 7
19
wb
A m
Fuerza sobre una masa magnética. Sustituyendo B por su equivalente de la
ecuación 1 en la ecuación  A , tenemos que:
2
F  m B
Donde F es la fuerza magnética que actúa sobre un polo magnético de masa m
al ser colocado en el seno de un campo mag nético B .
Comparación de las fuerzas gravitacional, eléctrica y magnética. La fuerza
gravitacional que actúa sobre un cuerpo es su propio peso, y de acuerdo con la
Segunda Ley de Newton, es:
w  m g
Siendo w el peso del cuerpo,
(aceleración e la gravedad g  9.8 sm2 ).
m
su masa y
g el campo gravitacional
La fuerza eléctrica que actúa sobre una carga eléctrica colocada en un campo
eléctrico es:
F  Q E
Donde F es la fuerza eléctrica, Q es la carga y E es el campo eléctrico. La
fuerza magnética al colocarla en el campo magnético es:
F  m B
Siendo F la fuerza magnética, m la masa magnética y B la inducción
magnética (campo magnético). Obsérvese que las ecuaciones:
w  m g
F  Q E
F  m B
Tienen la misma estructura, ya que en los tres casos, la fuerza que actúa sobre
m , Q y m (masa magnética) es producida por la presencia de un campo: g en el caso
gravitacional, E en el caso eléctrico y B en el caso magnético.
20
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No. 4
Explicar la existencia de cam pos m agnéticos debido al m ovimiento de cargas eléctricas.
Campos magnéticos generados por corriente eléctrica

Experimentos de Oersted
Descripción del experimento de Oersted. En 1820
Hans Christian Oersted (1777-1851), profesor danés, descubrió
que en las proximidades de un alambre con corriente existía un
campo magnético. Debido a la semejanza que existe en las
leyes que rigen la interacción entre cargas y entre polos
magnéticos, los físicos suponían que d ebía existir una relación
entre la corriente eléctrica y los fenómenos magnéticos, sin
embargo, los experimentos realizados no demostraron que tal
relación existiera, por tal motivo, y debido a que en sus
experimentos no había tenido éxito, Oersted estaba convencido de que no existiera tal
relación. Sin embargo, lo que ocurría era que el experimento estaba realizado.
N
S
Este consistía en colocar un alambre con corriente perpendicular a una brújula,
pero en 1820 por error colocaron el alambre con corriente paralelo a la brújula y ésta
se movió; al invertir el sentido de la corriente, la brújula se movió en sentido
contrario, lo que ponía de manifiesto que en las proximidades de un alambre con
corriente se genera un campo magnético.
Importancia del experimento de Oersted. Su importancia radica en el hecho
de que relaciona le electricidad con el magne tismo, naciendo, así, el
electromagnetismo.

Ley circuital de Ampere
Concepto de circulación. Considérese una trayectoria cerrada “  ”, la cual es
el contorno de una superficie abierta; cada elemento diferencial de este contorno lo
representaremos como un vector d  tangente a la trayectoria cerrada. La superficie
definida por la trayectoria cerrada es atravesada por un alambre que conduce una
corriente “ i ”. Esta corriente “ i ” produce un campo magnético en el espacio que
circunda el alambre. La evidencia experimental nos sugiere que este campo magnético
tiene la forma de un cilindro de radio indefinido y cuya densidad disminuye al
alejarse el alambre.
21
El
vector
de
inducción
magnética
es
B
perpendicular al alambre y siempre tangencial a la
B
trayectoria cerrada, en consecuencia, los vectores B y d 
son colineales.
Se define la circulación de “ B ” alrededor de la
trayectoria cerrada “  ” como.
d
l
Bd 
Este tipo de integral indica que la integral es cerrada
(es decir, sobre toda la trayectoria “  ”) y se lee la integral cerrada en B  d  .
Enunciado de la Ley Circuital de Ampere. Ampere
descubrió que la circulación de B en el contorno que rodea a un
alambre con corriente es proporcional a la corriente en el
alambre, lo que lo llevó a formular la l ey circuital de Ampere, o
simplemente la Ley de Ampere, cuyo enunciado es.
La integral cerrada del producto B  d  sobre una
trayectoria “  ” es igual a  o i .
Expresión matemática de la Ley de Ampere.
 Bd   
o
i
1
Donde:

B:
: Significa que la integral se efectúa sobre toda la trayectoria.
Es el vector de inducción magnética generada por el alambre.
d  : Es el vector tangente a la trayectoria y representa un elemento
diferencial de longitud.
i:
Es la corriente que circula por el alambre.
22
Regla de la mano derecha. Esta regla es útil para conocer
la dirección de B cerca de un alambre con corriente: Se toma el
alambre con la mano derecha, de modo que el dedo pulgar
indique la dirección de la corriente y los dedos restante enrolados
sobre el alambre indican la dirección de B .

Inducción magnética de un alambre recto
Consideraciones previas. Consideremos un alambre recto
por el que pasa una corriente “ i ”, esta corriente produce en el
espacio que rodea al alambre un campo magnético. Podemos
imaginarnos la f orma de este campo construyendo un cilindro imaginario cuyo eje es
el mismo alambre. En una dirección perpendicular al alambre, el campo magnético se
debilita a medida que nos alejamos del alambre.
Ecuación para calcular “ B ” cerca de un alambre recto. Nuestro objetivo es
deducir una ecuación que nos permita calcular la inducción magnética “ B ” en un
punto situado a una distancia “ r ” perpendicular al alambre, para lograrlo, usamos la
Ley de Ampere.
Bd   
o
i   B  d  cos 0 º
Pero B y d  son colineales, y como B es una constante, tenemos.
 B  d  cos 0 º   B  d   B  d   B 2 r   
B
o i
2 r
o
i
1
Que es la ecuación buscada. La dirección de B se determina usando la regla de
la mano derecha.
Ejemplo.
Calcular la inducción magnética a 10 cm de un alambre recto que conduce una
corriente de 5 A .
Datos :
r  10 cm
i5A
B
o  4   107
7
oi 4   10 Awbm  5 A

2 r
2  10 1 m 
B  105 T
23
wb
Am
Ejercicio.
Un alambre recto produce una inducción magnética de 6 10 6 T a una distancia
“ r ” del alambre. Calcular la inducción magnética a una distancia de 3r .
Un electrón se mueve a una velocidad de 210 6 ms paralelamente a un alambre
con una corriente de 2 A . El electrón se mueve en el mismo sentido de la corriente y a
5 cm del alambre.

a)
Calcular la fuerza sobre el electrón.
b)
¿La fuerza
constante?
sobre
el
electrón
aumenta,
disminuye
o
permanece
Ley de Biot-Savart
Conceptos preliminares. Cuando calculamos la inducción magnética cerca de
una alambre recto con corriente utilizamos una ecuació n que se deduce a partir de la
Ley de Ampere. En este caso la contribución al campo que produce cada elemento de
longitud es única, ya que las contribuciones de los elementos vecinos son anuladas
por los correspondientes elementos vecinos del otro lado.
No ocurre así cuando el alambre en cuestión es curvo, ya que al perderse la
simetría, las contribuciones dejan de ser iguales y, entonces, para calcular el campo
magnético en un punto habrá que considerar las contribuciones de todos los elementos
de la regió n. En este caso, la Ley de Ampere deja de ser funcional, siendo necesario
recurrir a una expresión conocida como Ley de Biot -Savart.
Expresión matemática de la Ley de Biot -Savart.
d

i
r 
Fig . 1
dB
 La Fig . 1 muestra una corriente “ i ” que circula en un alambre curvo, el
cual se puede considerar que está compuesto por un número
infinitesimal de elementos diferenciales d  , los cuales pueden ser
representados como vectores d  tangentes a la curva y en el mismo
sentido de la corriente.
 Cada elemento diferencial d  contribuye en un punto con un elemento
diferencial de la induc ción magnética d B . La inducción magnética es
un punto es la integral de todos los d B debidos a todos los d  .
B  d B
24
 En la Fig . 1 , un elemento d l produce en un punto un elemento d B . El
vector d B está dado por la ecuación.
dB
oi r
d
4  r 3
I 
Aplicando las reglas del producto vectorial, deducimos que el vector d B
penetra en la hoja del papel.
 Para obtener el vector B integramos.
B  d B
Efectuando esta integral en la ecuación I  , tenemos.
B
o i r
d
4  r 3
1
Ecuación que es conocida como la Ley de Biot -Savart, donde:

B:
: Significa que la integral se efectúa sobre una trayectoria cerrada.
Es la inducción magnética en las proximidades de un alambre con
corriente.
d  : Es un vector que representa a un elemento diferencial de longitud .
r:
Es el vector que va del elemento d  del alambre al punto donde se
evalúa B .
r:
Es la magnitud del vector (distancia que hay del elemento d del
alambre al punto donde se evalúa B .
 o : Es la permeabilidad del aire o vacío  o  4 10 7
25
wb
Am
.

Inducción magnética de una bobina
Ecuación para calcular la inducción magnética en el eje de una bobina
circular plana. Nuestro objetivo es deducir una ecuación que nos permita calcular la
inducción magnética en el eje de una bobina circular plana por la que pasa una
corriente “ i ”.
oi r
d  , resulta que d B es perpendicular a d  t a r , esta
4 r 3
perpendicular se aprecia en la Fig . 1 .
 Como d B 
 Podemos descomponer
d B en sus componentes rectangulares:
d Bp ,
perpendicular al eje “ x ” y d Bx sobre el eje “ x ”.
 Cada d B p generado por un d  es contrarestado por el vector opuesto, y
por lo tanto se anulan, quedando solamente d Bx .
 En la Fig . 2 se aprecia que d  y r son perpendiculares, entonces   90 º y
i 1
sen 90 º  1 , por lo tanto d B  o 2 d  .
4 r
 Se puede ver de la Fig . 1 que cos  
d Bx
, por lo tanto, d Bx  d B cos  ,
dB
entonces.
d Bx 
 o i cos 
d
4 r 2
 También, de la Fig . 1 se puede apreciar que cos  
entonces,
d Bx 
d Bx 
oi 1 R
d ,
4 r 2 r
reacomodando
oi R
d .
4 r 3
26
R
, donde r  R 2  x 2 ,
r
términos,
tenemos
 Integrando: B   d Bx , integral que es a lo largo de todo el contorno, por lo
tanto.
B
oi R
d
4 r 3 
Al integral, obtenemos la longitud de la espira.
B
oi R
oi R 2


2

R

4 r 3
2r3
Para una bobina de “ N ” espiras.
B
o N i R 2
2 r3
1
Que es la ecuación buscada.
En el centro de la bobina x  0 y entonces r  R , por lo tanto, la ecuación
anterior se reduce a la forma.
B
o N i
2
2R
En donde:
B : Es la inducción magnética en el eje y en el centro de una bobina circular
plana.
N : Es el número de espiras.
i : Es la corriente que circula por las espiras.
R : Es el radio de la espira.
r : Es la distancia del borde de la espira al punto donde se está evaluando
B , siendo r  R 2  x 2 y sonde x es la distancia del centro de la espira
al punto donde se está evaluando.
 o : Es la permeabilidad del aire o vacío  o  4 10 7
27
wb
Am
.
Ejercicios.
1.
Una bobina tiene 200 espiras de 3 cm de radio por las que circula una corriente
de 0.5 A , calcular B en el eje de la bobina a 4 cm del centro.
N  200
Datos :
i  0.5 A
o  4   107
R  3 cm  3  10 2 m
x  4 cm
r  R2  x2 
4 10

2000.5 A3 10
25  10 m 
B
o N i R 2
2 r3
 7 wb
Am
2
wb
Am
3 2  4 2
2
m
 5 cm
2
3
B  4.524  104 T
2.
En el centro de una bobina circular plana con espiras de 10 cm de radio, la
inducción magnética es B1 , y a una distancia x sobre el eje de la bobina la inducción
magnética se reduce a la mitad. Calcular el valor de x .
Datos :
R  10 cm
B2  12 B1
B1 
o N i
B2 
2R
o N i R 2
2 r3
Dividiendo miembro a miembro, tenemos.
B1 r 3
B
 3  1 1 2
B2 R
2 B1
r 3  2R 3
 r 3 2R
Como r  R 2  x 2 , entonces sustituyendo en r  3 2 R , se obtiene.
R2  x2  3 2 R
Elevando al cuadrado, despejando y sustituyendo R  10 cm .
R2  x2  3 4 R2
x2  3 4 R2  R2  R2
xR

3

4  1  10
x  7.66 cm
28

3

3

4 1

4 1
Ejercicios.
1.
En el centro de una espira circular de 3 cm de radio la inducción magnética es
de 10 5 T . Calcular la inducción magnética en el eje de la espira a 3 cm del centro
x  R  .
2.
En el centro de una bobina circular plana que tiene espiras de 6 cm de radio, la
inducción magnética es de 3.6 10 3 T y a una distancia x del centro, sobre el eje de la
bobina, la inducción magnética es de 4.5 10 4 T . Calcular el valor de x .

Excitación magnética
Concepto de excitación magnética. Se representa con la letra “ H ” y es la
intensidad del campo magnético que produce la bobina en el electroimán selenoide 
cuando circula corriente por dicha bobina.
Ecuación de la excitación magnética. Dicha excitación magnética es
proporcional al número “ N ”de espiras que tenga el solenoide, proporcional a la
corriente “ i ”que circula por las espiras e inversamente proporcional a la longitud del
selenoide.
Ni
P 
H

Introduciendo
la
unidad
como
constante
proporcionalidad P  se convierte en la ecuación.
H
de
proporcionalidad,
la
1
Ni

Donde:
H : Es la excitación magnética producida por la bobina de un electroimán
selenoide  .
N : Es el número de espiras que tiene la bobina.
i : Es la corriente que circula por las espiras.
 : Es la longitud de la bobina.
Unidades de la excitación magnética. Analizando la ecuación 1 , podemos
deducir que las unidades de la excitación magnética son .
Ampere  vuelta Ampere A


metro
metro
m
29
Factores de los que depende la excitación magnética. Al analizar la ecuación
1 , se deduce que la excitación magnética depende de la geometría de la bobina  N 

y de la corriente, pero no depende del material de que esta hecho el núcleo del
electroimán, el cual puede ser de aire o de hierro dulce).
Carácter vectorial de la excitación magnética. Al tratarse de una cantidad
vectorial, ésta tiene magnitud, dirección y sentido, el vector H es colineal con el
vector B y está localizado en el eje de la bobina.
Ejemplo.
Calcular la excitación magnética de un selenoide de 20 cm de largo con
100 vueltas de alambre por las cuales circula una corriente de 0.75 A .
Datos :
  20 cm
N  100
H
i  0.75 A
N i 100 0.75 A


2  10 2 m
H  375 mA
Ejercicios.
1.
Una bobina tiene 200 espiras de 3 cm de radio por las que circula una corriente
de 0.5 A , calcular B en el eje de la bobina a 4 cm del centro.
2.
Calcular la excitación magnética que produce la bobina de u n electroimán de
10 cm de largo con un devanado de 500 vueltas por la que circula una corriente de
0.6 A .
3.
Se tiene un selenoide de longitud  con 500 espiras por las que pasa una
corriente i produciendo una excitación magnética H . Un segundo selenoide tiene el
doble de largo que el anterior, consume la mitad de corriente y produce la misma
excitación magnética que el pr imero, ¿cuántas espiras tiene el segundo selenoide?.
30

Permeabilidad magnética
Concepto de permeabilidad magnética. Ésta se representa con la letra griega
 y es una característica propia de cada material, de la cual depende la inducción
magnética B , además de que se ha encontrado experimentalmente que la inducción
magnética de un selenoide aumenta considerablemente cuando se le introduce un
núcleo de un material ferromagnético y está definida por la ecuación.

1
B
H
Donde B es la inducción magnética del electroimán y H es la excitación
magnética de la bobina del electroimán. Analizando la ecuación 1 , deducimos que
las unidades de la permeabilidad magnética son.
weber
wb

Ampere  metro A  m
Permeabilidad del aire. En el aire o en el vació toma un valor de.
o  4 10 7
wb
Am
Se puede definir la permeabilidad del aire con la ecuación.
o 
2
Bo
H
En la que Bo es la inducción magnética del selenoide sin núcleo .
Permeabilidad relativa. Es la razón de la inducción magnética de un selenoide
con núcleo a la inducción magnética del selenoide sin núcleo. Ahora, sí B es la
inducción magnética del selenoide con núcleo y Bo es la inducción magnética del
selenoide sin núcleo, entonces, por la forma en que se definió a la permeabilidad
relativa, tenemos que.
r 
De esta ecuación, podemos
unidades, o sea, es adimensional,
éste cambia para cada material,
diferentes valores de B , aunque la
3
B
Bo
deducir que la permeabilidad relativa no tiene
además de que no tener un valor definido porque
e inclusive cambia en un mismo material para
permeabilidad relativa del aire vale 1.
31
Permeabilidad absoluta. A la permeabilidad magnética algunas veces se le
llama permeabilidad absoluta y se expresa como el producto de la permeabilidad
relativa por la permeabilidad del aire.
La permeabilidad magnética se definió con la ecuación 1 , la cual la podemos
escribir como.

 A
B Bo
BH
3,
B
y la ecuación
Bo
sustituyendo estos valores en la ecuación  A, tenemos.
Pero de acuerdo con la ecuación
r 
2,
o 
Bo
H
y
4
  ro
Ejemplos.
1.
La bobina de un electroimán tiene 600 vueltas por las que circula una corriente
de 0.2 A , el electroimán tiene 12 cm de largo y la inducción magnética que produce es
de 0.6 T . Calcular la permeabilidad magnética del núcleo.
Datos :
N  600
  12 cm  12  102 m
i  0.2 A
H
N i 00  0.2 A

 1 000 mA
2

12  10 m

B
0.6 T

H 1 000 mA
  6  104
2.
B  0.6 T
wb
Am
Un electroimán produce una inducción magnética de 0.6 T , y al retirarle el
núcleo de acero, la inducción magnética se reduce a 1.5 10 3 T , ¿qué valor tiene la
permeabilidad del núcleo?
Datos :
Bo  1.5  103 T
B  0.6 T
r 
B
0.6 T

 400
Bo 1.5  103 T
   r  o  400  4  107
  5.02  104
32
wb
Am
wb
Am
Ejercicios.
1.
La permeabilidad del núcleo de un electroimán es de 7.5 10 4
la permeabilidad relativa del núcleo?
wb
Am
, ¿cuánto vale
2.
Un selenoide con núcleo de aire produce un flujo magnético de 3 10 6 wb , y al
introducirle un núcleo de acero, el flujo magnético aumenta a 9 10 6 wb . Calcular la
permeabilidad del núcleo.

Permeabilidad magnética de un selenoide
Un selenoide es un alambre largo enrollado en una espiral apretada formando
N espiras que, en conjunto, le dan al selenoide una longitud  .
i
Fig . 1
B
        

La Fig . 1 representa el corte de un selenoide, donde la corriente i que
pasa por las espiras, sale de la hoja por arriba y entra en la hoja por
abajo. Aplicando la regla de la mano derecha, se deduce que en la
parte interna del selenoide, B apunta hacia la derecha; la inducción
magnética total es la suma de las contribuciones que cada espira
genera en la parte interna del selenoide.

En el exterior del selen oide el campo es tan débil que puede
despreciarse; solo en su interior el campo tiene una intensidad
considerable.

Un selenoide con corriente presenta las características de un imán; la
cara por donde salen las líneas de inducción tiene polaridad norte, y la
cara por donde entran tiene polaridad sur.
33
Ecuación para calcular B de un selenoide con núcleo ferromagnético. El
objetivo es deducir una ecuación que nos permita calcular la inducción magnética B
en el eje de un selenoide de longitud l con N espiras por las que pasa una corriente
i . Puesto que la permeabilidad magnética se define como.

B
H
En donde.
BH
Ahora bien, la excitación magnética de un selenoide es H 
B
Ni

Ni
, por lo tanto.

1
Que es la ecuación buscada. Dado que la permeabilidad magnética se puede
expresar como    r  o , la ecuación 1 se puede escribir como.
B
r o N i

2
Ecuación para calcular B de un selenoide con núcleo de aire. Si el selenoide
no tiene núcleo (o es de aire), entonces  r  1 y la ecuación 2 se rescribe como.
B
r Ni

3
Para las ecuaciones 1, 2 y 3 .
B : Es la inducción magnética.
N : Es el número de espiras del selenoide.
i:
Es la corriente que circula por las espiras.
 : Es la permeabilidad magnética.
 r : Es la permeabilidad relativa.
 o : Es la permeabilidad del aire.
:
Es la longitud del selenoide.
34
Ejemplo.
Un selenoide de 15 cm de largo tiene 300 espiras por las que pasa una corriente de
0.4 A . Calcular la inducción magnética B .
Datos :
2
  15 cm  15  10 m
B
o N i

N  300
4 10

7 wb
Am
i  0.4 A
3000.4 A
15  10 2
B  103 T

Inducción Magnética de un toroide
El toroide se puede considerar como un caso particular del selenoide, el cual ha
sido unido por sus extremos formando una rosca de N espiras. Se le llama radio
medio r a la distancia que hay del centro del toroide al centro de las espiras.
r
Fig . 1
Las líneas de inducción son circunferencias confinadas en el área de sección
transversal A del toroide y la longitud media del toroide es la circunferencia barrida
por el radio medio del toroide.
r
A
Fig . 2
La longitud media del toroide es la circunferencia barrida por el radio medio
del mismo: l  2 r .
35
Ecuaciones para calcular el B del toroide. La inducción magnética B es
similar a la de un selenoide y puede ser expresada en función de la longitud del
toroide o del radio medio. Para expresar B en función de la longitud del toroide se
usan las mismas ecuac iones que para el selenoide.
B
Ni

Escribiendo    r  o .
B
r o Ni

Pero si el núcleo del toroide es de aire,  r  1, entonces.
B
Ni

Y detallando B en función de r : l  2 r , entonces.
B
Ni
2 r
1
Pero    r  o , entonces.
B
r o N i
2 r
2
Si el núcleo es de aire,  r  1, entonces.
B
o N i
2 r
36
3
Ejemplos.
1.
Un selenoide produce una inducción magnética de 2 10 3 T y al introducirle un
núcleo de acero la inducción magnética aumenta a 1.2 T . Calcular la permeabilidad
relativa del núcleo.
Datos :
B o  2  103 T
r 
B  1.2 T
B
1.2 T

B o 2  10 3 T
 r  600
2.
Un toroide tiene 600 espiras por las que pasa una corriente de 0.5 A , el radio
medio del toroide es de 10 cm y la permeabilidad relativa del núcleo vale 500 .
Calcular la inducción magnética B .
Datos :
N  600
i  0.5 A
r  10 cm
 r  500
 r  o N i 500 4   107 Awbm  600 0.5 A
B
2 r
2  101 m
B  0.3 T
Ejercicios.
1.
Un selenoide de 500 espiras produce una inducción magnética B , un segundo
selenoide tiene la mitad de largo que el anterior y consume la misma corriente, pero
produce el doble de inducción magnética que el primero, calcular el número de
espiras del segundo selenoide.
2.
La inducción magnética de un selenoide es 10 3 T . Calcular la inducción
magnética si el selenoide se comprime y su longitud se reduce un 20 % .
3.
Un toroide tiene 600 espiras y un radio de 15 cm , la permeabilidad relativa del
núcleo es de 500 . Calcular la corriente necesaria para obtener una inducción
magnética de 0.12 T .
4.
La inducción magnética de un toroide es de 0.1 T , calcular la inducción
magnética de este toroide cuando a su bobina se le quita el 10 % de sus espiras.
37

Curva de magnetización
Considérese un electroimán cuyo núcleo está constituido por un material
ferromagnético que nunca ha estado bajo la, influencia de un campo magnético, ante
estas condiciones, y si no circula corriente por la bobina del electroimán, la
inducción magnética debe ser cero. Como hemos visto antes, la excitación magnética
depende de la geometría de la bobina y de la corriente, dado que la geometría es
constante, podemos decir que la excitación es una función lineal que de depende de la
corriente, o sea.
H  H i 
Sí la corriente varía desde un valor de cero hasta un valor “ i ”, entonces la
excitación variará de cero hasta “ H ”, sin embargo, se ha observado q ue sí el aumento
de “ H ” es constante, el aumento de “ B ” no lo es, ya que es un principio que “ B ”
vale cero y al aumentar la corriente, “ B ” aumenta rápidamente, pero a medid a que la
corriente, y “ H ”, crece el aumento de “ B ” es más lento hasta volverse casi
logarítmico. La razón de esto es que la permeabilidad
de los materiales
ferromagnéticos no es constante, teniendo un valor muy grande al principio y después
tiende a decrecer.
Se piensa que esta disminución de la permeabilidad obedece al alineamiento de
los dipolos del material provocando por la excitación magnética, que al principio es
grande porque casi todos están desalineados , pero al aumentar la excitación
magnética, aumenta la temperatura del material, lo que provoca es el desalineamiento
de los dipolos y, en consecuencia, hay una disminución de la permeabilidad.

B  B H 
B
   H 
H
La relación entre “ H ”, “ B ” y “  ” puede ser graficada, y esta gráfica se
conoce con el nombre de curva de magnetización, donde las relaciones  H  y BH 
no son lineales, esto obedece a que “  ” no es constante, y por lo tanto, el
decrecimiento de “ B ” no es uniforme.
38
Interpretación de la cueva de magnetización. En un principio, el
alineamiento de los dipolos es rápido por la influencia de la excitación magnética que
crece, pero al aumentar la corriente, aumenta la temperatura del material, provocando
el desalineamiento de los dipolos y, entonces, la permeabilidad disminuye, es por esta
razón que al principio la inducción magnética aumenta rápidamente, pero después
crece muy lentamente.

Ciclo de histéresis
El término histéresis se refiere a la historia magnética del material. Si un
material ferromagnético nunca ha estado bajo l a influencia de un campo magnético,
no presentará propiedades magnéticas, y en estas
condiciones, la inducción magnética y la excitación
B
a
magnética coinciden: ambas son cero.
Pero si después este material ferromagnético es
usado como núcleo de electroimán y se pasa corriente
por la bobina, la excitación magnética y la inducción
magnética ya no coincidirán, pues aunque ya no pase
H  0 , el material
corriente
por
la
bobina
ferromagnético conservará cierto magnetismo residual.
A este retraso de la magnetización con respecto a
la excitación magnética se le denomina histéresis.
b
c
0
f
H
e
d
Fig . 1
En el origen de la Fig . 1 no circula corriente por la bobina y tanto la excitación
como la inducción magnética valen cero. En el punto “ a ” la inducción magnética
alcanza un cierto valor al circular corriente por la bobina.
En el punto “ b ” ha desaparecido la corriente y el valor de H es cero, pero B
es diferente de cero, el material ha conservado un magnetismo residual. En el punto
“ c ” la corriente circula en sentido contrario, haciendo que el magnetismo residual
desaparezca B  0 . En el punto “ d ” ha aumentado la corriente en sentido contrario
hasta que B alcanza cierto valor.
En el punto “ e ” la corriente ha desaparecido y el valor de H es cero, pero B
es diferent e de cero, otra vez el material ha conservado un magnetismo residual. En el
punto “ f ” ha tenido que circular corriente en el sentido inicial y H tiene un cierto
valor para que el magnetismo residual desaparezca B  0 . En el punto “ a ”, H crece
al aumentar la corriente y B alcanza un cierto valor.
En general, se observa que hay un cierto retraso de la magnetización con
respecto a la exci tación magnética. A este retraso se le denomina histéresis, y forma
al ciclo de histéresis .
39
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No 5
Explicar la interacción entre
eléctricam ente en m ovim iento .
los
campos
m agnético s
y
las
partículas
cargadas
Fuerzas magnéticas

Fuerzas sobre una carga en movimiento
Cuando una carga se mueve con velocidad “ v ” en un campo magnético, actúa
sobre ella una fuerza que la desvía perpendicularmente a su dirección inicial y al
campo.
B
Fig . 1




































Qv
F
Ecuación vectorial de la fuerza sobre una carga en movimiento. Una
característica notable de las fuerzas magnéticas sobre cargas es que se respetan las
reglas de un producto vectorial, lo que hace predecible su comportamiento una vez
conocida la dirección del campo magnético y la dirección de la carga en el momento
de entrar al campo. La ecuación vectorial
que nos sirve para describir el
comportamiento de la carga (de acu erdo con las reglas del producto vectorial) es.
F  Qv B
1
Ecuación que nos sirve para determinar la dirección y el sentido de la fuerza
sobre una carga. La ecuación escalar asociada a la ecuación 1 es.
F  Q v sen 
40
2
La cual nos sirve para determinar la magnitud de la fuerza que actúa sobre la
carga y donde.
Q v : Es el vector que nos sirve para determinar la dirección de la carga.
Q : Es la carga en movimiento.
v : Es la magnitud de la velocidad v .
B : Es la magnitud del vector B .
 : Es el ángulo entre los vectores Q v y B .
F : Es la magnitud del vector F .
Consideraciones complementarias. Existen cuatro causas por las que la fuerza
sobre la carga puede ser cero.
Fmax
1.
v0
2.
B0
3.
Q v y B son colineales sen 0 º  sen 180 º  0 .
4.
Existe otra fuerza que anule el efecto de la fuerza magnética.
La fuerza es máxima cuando Q v y B son perpendiculares sen 90 º  1 , entonces
 Q v B , por lo tanto, la ecuación 2 se puede escribir como.
F  Fmax sen 
Ejemplo.
En la figura, la carga de 10 6 C lleva una
velocidad de 10 6 ms y penetra formando un ángulo
Qv
de 30 º con un campo magnético de 10 2 T .

B
a)
Calcular la dirección de la fuerza sobre la
carga.
b)
Calcular la magnitud de la fuerza.
Solución.
F  Q v  B . La carga penetra perpendicularmente a la hoja de papel, por lo
a)
tanto, la carga se desviará hacia adentro de la hoja.
b)


F  Q v B sen   10 6 C 106
m
s
10 T  sen 30 º  5 10
2
41
3
N
Ejercicios.
1.
Un protón se mueve de izquierda a derecha con una velocidad de 10 7 ms y entra
en un campo magnético de 0.4 T que penetra perpendicularmente a la hoja de papel,
calcular el valor de F .
2.
Un núcleo de helio se mueve con una velocidad de 210 6 ms y penetra formando
un ángulo de 30 º con un campo magnético de 0.5 T , calcular el valor de la fuerza.
3.
Un electrón se mueve de izquierda a derecha con una velocidad de 10 7 ms y entra
en un campo magnético de 0.5 T que penetra perpendicularmen te a la hoja de papel.
Calcular el valor de la fuerza.
42

Fuerza de Lorentz
La llamada Fuerza de Lorentz, llamad así en honor al físico holandés Enrique
Lorentz (1853 -1928), es la superposición de una fuerza magnética y una fuerza
eléctrica sobre una carga en movimiento. Cuando la carga “ q ” penetra con una
velocidad “ v ” en un campo magnético, actúa sobre ella una fuerza magnética.
Fm  q v  B
Cuando la carga “ q ” penetra en un campo eléctrico, actúa sobre ella una fuerza
eléctrica.
Fe  q E
Sí los campos magnético y eléctrico se hallan superpuestos (en forma
perpendicular), las fuerzas magnética y eléctrica se combinan y la fuerza total sobre
la carga es F  F m  F e , o sea.
F  qv B  q E
1
La fuerza magnética F m es perpendicular a q v y a B y obliga a la carga a
desviarse en una dirección perpendicular a su dirección inicial.
La fuerza eléctrica F e es colineal a E y obliga a la carga a moverse en la
dirección del campo si “ q ” es positiva, o en dirección contraria al campo si “ q ” es
negativa. En general consideraremos que “ q ” es positiva.
1
La fuerzas F m y F e son colineales y la suma vectorial indicada por la ecuación
se reduce a una suma algebraica. Sin embargo, las fuerzas a veces se suman y a
veces se restan, por lo tanto, la ecuación escalar asociada a tal ecuación es
F  F m  F e , o sea.
F  q v B sen   q E
43
2
Si la carga se mueve en dirección perpendicular al campo magnético,   90 º y
entonces la ecuación 2 se reduce a.
3
F  qv B  q E
En donde:
F : Es la magnitud del vector F .
Q : Es la carga en movimiento.
v : Es la magnitud de la velocidad de la carga .
B : Es la magnitud del vector B .
 : Es el ángulo entre los vectores q v y B .
E : Es la magnitud del vector E .
Consideraciones complementarias. Si las fuerzas se suman, la fuerza total es
mayor que la fuerza magnética y si las fuerzas se restan, la fuerza total es menor que
la fuerza magnética, inclusive, puede ser cero.
Fig . 1 Las fuerzas magnética y eléctrica son colineales, y como tienen la misma
dirección, la fuerza total sobre la carga es mayor que la fuerza magnética.
Fig . 2 Las fuerzas magnética y eléctrica son colineales, pero como tienen
direcciones contrarias, la fuerza total sobre la carga es menor que la fuerza
magnética.
E
Fe
qv
qv
E
Fm
Fig . 1
B
Fe
Fig . 1
44
Fm
B
Ejemplo.
1.
En la Fig . 1 , una carga de 10 6 C se mueve con una velocidad de 10 6
y E  210 4
N
C
m
s
, B  10 2 T
. Calcular el valor de la fuerza total sobre la carga.
Puesto que F m y F e son colineales, se suman.
Datos :
6
q  10 C
v  10
B  10  2 T
6 m
s
F  Fm  Fe  q v B  q E  106 C 106
m
s
E  2  10 4
N
C
10 T   10 C 2 10 
2
6
4 N
C
F  3  102 N
Ejercicios.
1.
Una carga penetra con una velocidad de 210 6 ms perpendicularmente a un
campo magnético y a uno eléctrico, la inducción magnética vale 0.5 T . Calcular el
valor del campo eléctrico para que la fuerza total sobre la carga sea nula.
2.
Una carga penetra con velocidad de 210 6 ms perpendicularmente a un campo
magnético y a uno eléctrico, la inducción magnética vale 0.5 T . Calcular el valor del
campo eléctrico para que la fuerza total sobre la carga sea el doble de la fuerza
magnética.
3.
En la Fig . 2 una carga se mueve con una velocidad de 10 5 ms y el campo
magnético vale 0.5 T . Calcular el valor del campo eléctrico para que la fuerza total
sobre la carga sea un medio de la fuerza magnética.
45
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No.6
Explicar la interacción entre el cam po m agnético y un conductor con corriente eléctrica.

Fuerza sobre un alambre con corriente
Ecuaciones. Sea un alambre de longitud “  ” por el cual circula una corrient e
“ I ”. Este alambre se coloca en el seno de un campo magnético, de modo que la
dirección de la corriente forma un ángulo “  ” con la dirección del campo magnético.
La evidencia experimental pone de manifiest o que en estas circunstancias, una fuerza
lateral actúa sobre el alambre desplazándolo perpendicularmente a la dirección de la
corriente. Nuestro objetivo es deducir las ecuaciones escalar y vectorial de la fuerz a
sobre el alambre. Cualquier carga “ Q ” que se mueva por el alambre con velocidad
“ v ”, recorrerá la distancia “ l ” en un tiempo “ t ”, de modo que.
v

t
 A
Y la fuerza sobre esta carga es.
F  Q v B sen 
B
Sustituyendo “ v ” de  A en B  , tenemos.

F  Q B sen 
t
Reacomodando términos.
F
Pero como
Q
 B sen 
t
C 
Q
 I , y sustituyendo en C  , obtenemos.
t
F  I  B sen 
1
Que es la ecuación buscada. Analizando esta ecuación, observamos.
 La ecuación 1 nos da la magnitud de la fuerza pero no nos da
información en cuanto a la dirección y el sentido de ésta.
 La estructura de la ecuación 1 es característica de un producto vectorial,
por lo tanto, debe tener una ecuación vectorial asociada, la cual es.
46
2
F  I B
En donde:
F : Es la magnitud del vector F .
I : Es la intensidad de corriente en el alambre.
 : Es la longitud del alambre.
I l : Es el vector cuya dirección está dada por el sentido de la corriente.
B : Es la magnitud del vector B .
 : Es el ángulo entre los vectores I l y B .
Consideraciones complementarias.
 Con la ecuación 1 podemos calcular la magnitud de la fuerza lateral que
actúa sobre el alambre.
 La ecuación 2 nos permite determinar la dirección y el sentido de la
fuerza sobre el alambre. Como sabemos (por la definición del producto
vectorial), el vector F debe ser perpendicular tanto al vector I  como
al vector B .
 Si el alambre es perpendicular al campo magnético,   90 º y por lo tanto
la fuerza sobre el alambre es máxima porque sen 90 º  1 , y en este caso
la ecuación 1 se reduce a.
F  I B
3
F
B

l
Fig . 1
47
I
En la Fig . 1 , el vector I  se localiza en el eje del alambre y en la d irección de
la corriente. El vector F sale perpendicularmente a la hoja de papel, empujando al
alambre hacia fuera del plano formado por I  y B .










F



























x
I

Fig . 2
En la Fig . 2 , el campo magnético penetra perpendicular a la hoja de papel y el
vector I  apunta hacia arriba. La fuerza magnética sobre el alambre lo empuja haci a
la izquierda.
Efecto motor. Es el efecto que presenta un alambre con corriente al ser
desplazado lateralmente cuando se le coloca en un campo magnético, ya que es el
principio en que se basa el funcionamiento del motor eléctrico.
Ejemplos.
1.
Calcular la fuerza que actúa sobre un alambre recto de 50 cm de largo por el
que circula una corriente de 0.4 A si se sitúa perpendicularmente a un campo
magnético de 0.8 T
Datos :
  50 cm  5  10 1 m
I  0.4 A
B  0.8 T
  90 º
F  I  B  0.4 A 5 101 m 0.8 T 
F  0.16 N
48
2.
Por un alambre de 40 cm de largo circula la una corriente de 0.2 A y que forma
un ángulo “  ” con un campo magnético de 10 2 T y sobre él cual actúa una fuerza de
6.93 10 4 N , calcular el valor de ángulo.
Datos :
1
  40 cm  4  10 m
F  I  B sen 
B  10  2 T
I  0.2 A
 sen  
F  6.93  10  4 N
F
6.93  10 4 N

 0.866
I  B 0.2 A 4  10 1 m 10  2 T



  arc sen 0.866
  60 º
Ejercicios.
1.
Al colocar un alambre recto con corriente formando un ángulo de 30 º en el
seno de un campo magnético, actúa una fuerza sobre el alambre de 0.4 N , calcular el
máximo valor de la fuerza sobre el alambre.
2.
Un alambre de 15 cm de largo
con una masa de 15 g se suspende
horizontalmente perpendicular a la hoja de papel. Calcular la intensidad y el sentido
de la corriente necesaria para que el peso del alambre se anule.

Fuerza entre alambres paralelos
El objetivo es deducir una ecuación que nos permita calcular la fuerza con que
se atraen o se rechazan dos alambres paralelos que conducen una corriente.
 Considérense dos alambres paralelos, a los que llamaremos “ a ” y “ b ”, los
cuales conducen corrientes “ i a ” e “ i b ”.
 Los alambres tienen una longitud “  ” o son de longitud infinita.
 Los alambres están separados una distancia “ d ”.
 Ambos alambres producen un campo magnético de la forma.
B
o i
2 d
49
El hecho de que en el denominador aparezca “ d ” en lugar de “ r ” significa que
el campo magnético producido por un alambre se va a evaluar donde esta el otro. Por
ejemplo, si en donde esta el alambre “ a ” evaluamos el campo magnético producido
por el alambre “ b ”, tenemos.
B
 o ib
2 d
I 
 Ambos alambres están sometidos a una fuerza de la forma.
F  i B
Donde “ B ” es el campo magnético producido por cualquiera de los dos
alambres. Por ejemplo, la fuerza sobre el alambre “ a ” es.
F  i b  Bb
II 
Sustituyendo B b de I  en II  , tenemos.
F
 o ia ib
2 d
1
Que es la ecuación buscada.
Sin embargo, si se trata de dos alambres infinitamente largo, no se puede usar
directamente la ecuación 1 porque la fuerza sería infinita, en este caso lo que se
debe considerar es la fuerza por unidad de longitud.
F  o ia ib


2 d
2
En donde:
F:
Es la magnitud de la fuerza con que dos alambres paralelos que
conducen corrientes “ i a ” e “ i b ” se atraen o se rechazan.
F
: Es la magnitud de la fuerza por unidad de longitud con que dos

alambres de longitud infinita que conducen corrientes “ i a ” e “ i b ” se
atraen o se rechazan.
 : Es la longitud de los alambres (cuando no son de longitud infinita).
d : Es la distancia que separa a lo dos alambres.
50
Consideraciones complementarias.
 Si los alambres son de longitud infinita, la fuerza entre éstos se mide en
Newtons, N , pero si los alambres son de longitud infinita, la fuerza por
Newton N
unidad de longitud se mide en
, .
metro m
 En cualquiera de los dos alambres, la fuerza es perpendicular a “ i  ” y a
“ B ”, y por lo tanto, los alambres se atraen o se rechazan.
De acuerdo con la Fig . 1 el vector B b sale de la hoja de papel y el vector B a
penetra perpendicularmente a la hoja, por lo tanto, la fuerza entre los alambres es de
atracción.
Según la Fig . 2 , las dos corrientes tiene el mismo sentido y penetran
perpendicularmente a la hoja de papel, siguiendo la regla de la mano de recha se
determina la dirección de los vectores B a y B b .
ia
ib
Ba
Ba
F
F
B b
l
a 
F
F 
b
d
Bb
Fig . 1
Fig . 2
 Los dos alambres están sometidos a una fuerza de la fo rma F  i  B , y
siguiendo la regla del producto vectorial, deducimos que cosido las
corrientes son del mismo sentido, los alambre se atraen ( Fig . 1 y
Fig. 2 ), y cuando las corrientes son de sentidos contrarios, los alambres
se repelen ( Fig . 3 y Fig. 4 ).
ia
Bb
F
Bb 
B a
d
F
F
l
Ba
a
b
ib
Fig . 3
Fig . 4
51
F
De la Fig . 3 , cuando las corrientes son de sentido contrario, los alambres s e
rechazan, y si la dirección de los vectores B a y B b se determina con la regla de la
mano derecha, y siguiendo las reglas del producto vectorial, se de termina la dirección
de la fuerza, Fig . 4 .
Definición del Ampere. Dos alambres de longitud infinita están separados 1 m
y conducen corrientes iguales, y cuando la corriente en ambos alambres es de 1 A , la
fuerza por unidad de longitud entre los alambres es.


2
4  10 7 Awbm 1 A
F o i


 2 10 7
 2 d
2  1 m
2
N
m
Por lo cual se define al ampere así.
“Es la corriente establecida en dos alambres de longitud infinita
separados 1 m que produce una fuerza por unidad de long itud
entre los alambres de 2 10 7
N
m
”
Ejemplos.
1.
Dos alambres de 80 cm de largo están separados 10 cm y conducen corrientes
iguales de 0.4 A . Calcular la fuerza de atracción entre los alambres.
Datos :
1
d  10 cm  10 1 m
  80 cm  8  10 m
ia  ia
i a  i a  0.4 A
 ia ia  i 2
 o  i 2 4   107 Awbm  8 10 1 m0.4 A 2
F

2 d
2  101 m
F  2.56  107 N
52
2.
Dos alambres de longitud infinita están separados 20 cm y conducen corrientes
iguales de 0.5 A , calcular la fuerza por unidad de longitud.
Datos :
d  20 cm  2  10 1 m
i a  i b  i  0.5 A


2
4   10 7 Awbm 0.5 A
F o i


 2 d
2  10 1 m 
F
 2.5  10 7

2
N
m
Ejercicios.
1.
Dos alambres de longitud infinita que conducen corrientes tales que una es el
doble de la otra y se atraen con una fuerza por unidad de longitud de 8 10 7 Nm cuando
están separadas 2 cm . Calcular el valor de las dos corrientes.
2.
Dos alambres de longitud infinita que conducen corrientes iguales se atraen con
una fuerza por unidad de longitud de 2.4 10 6 Nm cuando están separadas 3 cm . Calcular
el valor de las corrientes.
3.
Los tres alambres de la figura son de
longitud infinita y están ubicados en el mismo
plano, por lo tanto, las fuerzas entre los alambres
con coplanares. El alambre “ a ” ejerce una fu erza
de atracción sobre el alambre “ b ”, la cual es
contrarestada por la fuerza de atracción que el
alambre “ c ” ejerce sobre el alambre “ b ”. Si la
fuerza neta sobre el alambre “ b ” es cero, e
i a  0.3 A , calcular el valor de la corriente i c .
53
ia
ib
ic
2d
d
Fig . 3
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No. 7
Explicar que la interacción entre conductores y cam pos m agnéticos se aplica en
dispositivos de m edición y m aquinaria eléct rica.
Instrumentos de medición

Galvanómetro
Concepto y utilidad del galvanómetro.
 El galvanómetro es un dispositivo que sirve para medir corrientes
pequeñas.
 Su funcionamiento se basa en el efecto motor y los tipos de galvanómetro
que veremos son el de D’Arsonval y el de cuadro móvil.
Galvanómetro de D’Arsonval.
 El imán de herradura proporciona el campo magnético.
 El cilindro de hierro dulce, además de servir de apoyo a la bobina, sirve
para concentrar las líneas de inducción.
 El conjunto del cilindro y de la bobina están sostenidos por un fino hilo
conductor (suspensión).
 El resorte sirve para amortiguar las vibraciones del sistema.
 Al pasar corriente por la bobina, debido al afecto motor, aparece un
momento que la obliga a girar.
 El alambre produce un momento recuperador que contrarresta el momento
producido por la corriente. La bobina se detiene cuando los momentos
son iguales.
 Un haz luminoso se hace incidir sobre el espejo, y al ser reflejado, indica
en una escala el ángulo desviado, con lo cual es posible conocer la
intensidad de corriente que pasa por la bobina.
 Al suspenderse la corriente, la bobina regresa a su posición inicial.
54
Imán de herradura
Suspensión
Espejo
N
Bobina
S
Cilindro de hierro dulce
Resorte
Galvanómetro de cuadro móvil. El funcionamiento de este galvanómetro
también se basa en el efecto motor.
 El imán de herradura proporciona el campo magnético, se han añadido dos
piezas polares que le dan al campo magnético una configuración
radial.
 La bobina va montada en el cilindro de hierro dulce, el cual va pivoteado
sobre dos asientos de ágata.
 Al circular corriente por la bobina aparece un momento mecánico que
obliga al cilindro a girar. El desplazamiento angular es proporcional a
la intensidad de la corriente.
 Al girar el cilindro, mueve a la aguja indicando que va soldada a él; esta
aguja se desplaza sobre una escala graduada, lo que permite leer
directamente la cantidad e corriente que pasa por la bobina.
 Los dos muelles tienen una doble función: Hacer llegar la corriente a la
bobina y producir un momento recuperador cuando gira el cilindro. La
aguja se detiene cuando el momento sobre la bobina y el momento
recuperador son iguales.
 Al suspenderse la corriente, el cilindro regresa a s u posición inicial.
 El rozamiento producido por los cojinetes de ágata es pequeño, pero es
mayor que el producido por la torsión del hilo, por consiguiente, los
momentos desviador y recuperador han de ser mayores que el
galvanómetro de cuadro móvil. Una co nsecuencia de esto es que los
galvanómetros de cuadro móvil son menos sensibles que los de
D’Arsonval, pero en cambio son más versátiles.
55
Imán de herradura
Escala
Aguja
indicadora
Piezas
polares
Muelle
Cilindro de
hierro dulce
Bobina
S
N
Funcionamiento de un galvanómetro como amperímetro o voltímetro.
 Considerando que la desviación de la bobina del galvanómetro es
proporcional a la corriente, se puede graduar el aparato para medir
intensidad de corriente y f uncionar como amperímetro.
 Como la bobina tiene una cierta resistencia porque está hecha de alambre y
cumple con la Ley de Ohm, la corriente de la bobina es proporcional a
la diferencia de potencial entre los bornes del aparato, en consecuenci a
se puede graduar el galvanómetro para medir la diferencia de potencial
y funcionar como voltímetro.
Por ejemplo, supongamos que la resistencia interna del galvanómetro es de
20  y que la aguja de desvía toda la escala para una corriente de 10 mA . La


diferencia de potencial entre los bornes es V  I r  10 10 3 A 20   0.2 v . La escala,
por consiguiente, puede graduarse para medir de cero a 10 mA o de cero a 0.2 v .
Conversión de un galvanómetro en un amperímetro.
 Para poder realizar esta conversión, se le conecta una pequeña resistencia
de derivación (en paralelo).
 El amperímetro debe conectarse en serie en el circuito, ya que e pretende
que toda la corriente pase por él.
 Si toda la corriente que pasa por el amperímetro pasara por la resistencia
“ r ” del galvanómetro, ésta se quemaría; para evitar esto se requiere
que la resistencia del galvanómetro sea pequeña, pero no se puede
construir una bobina con alambre muy grueso. El problem a se resuelve
conectando en paralelo una resistencia “ R ” más pequeña que “ r ”.
56
I
A
G
r
I1
I2
R
Conversión de un galvanómetro en un voltímetro.
 Para realizar esta conversión, se le conecta una gran resistencia en serie
al galvanómetro.
 El voltímetro se debe conectar en paralelo en el circuito, ya que se
pretende que pase poca corriente a través de él, para lo cual su
resistencia debe ser muy grande.
V
I

R
r
G
Amperímetro
Aumento en el rango de un amperímetro. Considérese un amperímetro con un
rango I 1 y una resistencia interna R 1 . Se desea aumentar el rango de est e
amperímetro de modo q ue su aguja se deflecte toda la escala para una corriente I .
Aumentar el rango del amperímetro significa que si inicialmente la aguja del aparato
se reflecta toda la escala para medir una corriente I 1 ahora deflectará toda la escala
para medir una corriente I , siendo I un múltiplo de I 1 . En consecuencia, para una
corriente I 1 , la aguja se deflectará solo una parte de la e scala.
Para no dañar la resistencia del aparato con un exceso de corriente se le
conecta en paralelo una resistencia más pequeña, la cual llamaremos R 2 (conocida
como resistencia de derivación) y por la cual pasará la corriente excedent e I 2 .
Resistencia de derivación. El objetivo es deducir una ecuación que nos
permita calcular la resistencia de derivación para aumentar el rango de un
amperímetro.
R1
I
B
A I1
I2
Fig . 1
R2
57
Donde R 1 y R 2 están en paralelo y a la misma diferencia de potencial. En el
nodo “ A ” se tiene que I  I 1  I 2 , por lo tanto.
I 1R1  I 2 R 2
 R2
I 1R1
 A
I2
Y como I  I 1  I 2 , entonces I 2  I - I 1 , lo cual se sustituye en la ecuación  A .
R2 
I 1R1
1
I  I1
Que es la ecuación buscada.
Factor de cambio de escala. Se le llama factor de cambio de escala al la razón
de los rangos de corriente.
n
I
I1
 I  nI1
 A
La resistencia de derivación se puede calcular en función del factor de cambio
de escala, sustituyendo I de  A en la ecuación 1 .
R2 
I 1 R1
n I 1  I1

I 1 R1
I 1 n  1

R1
2
n 1
En donde.
R 1 : Es la resistencia interna que inicialmente tenía el amperímetro.
R 2 : Es la resistencia de derivación.
I:
Es la corriente del nuevo rango.
I 1 : Es la corriente del rango inicial.
n : Es el factor de escala.
Resistencia interna equivalente. Se le llama resistencia interna equivalente,
R eq , a la resistencia del amperímetro con el nuevo rango. Como R 1 y R 2 están en
paralelo, R eq debe ser menor que cualquiera de las dos. Para calcularla.
R eq 
1
1
1

R1 R 2

R1 R 2
R1  R 2
58
B 
Pero como R 2 
I 1 R1
I  I1
, entonces R 1  R 2 
R eq 
I R2
I
, lo cual se sustitu ye en B  .
1
R1 R 2 I 1
  R1
I R2
I
I1
3
La resistencia interna equivalente se puede calcular en función del factor de
cambio de escala. Si consideramos que I  n I 1 , entonces.
R eq 
I 1R1
nI1

R1
4
n
Ejemplos.
1.
Un amperímetro tiene un rango de 1 A y una resistencia interna de 0.4  . Se
desea aumentar el rango a 5 A .
a)
Calcular la resistencia de derivación.
Datos :
I1  1 A
I 5A
R2 
I 1 R1
I  I1

R1  0.4 
1 A 0.4 
5 A 1 A
R 2  0.1 
b)
Calcular la resistencia interna del nuevo amperímetro.
R eq 
1 A 0.4 
I1
 R1 
I
5A
R eq  0.08 
59
2.
Un amperímetro tiene una resistencia interna de 0.6  . Se desea aumentar el
rango del amperímetro hasta cuatro veces el rango inicial.
a)
Calcular la resistencia de derivación.
Datos :
R1  0.6 
R2 
n4
R1
n 1

0.6 
3
R 2  0.2 
b)
Calcular la resistencia interna del nuevo amperímetro.
R eq 
R1
n

0.6 
4
R eq  0.15 
Ejercicios.
1.
Un amperímetro tiene un rango de 2 A y una resistencia interna de 0.4  . Para
aumentar el rango se le conecta en paralelo una resistencia de 0.2  , calcular el
nuevo rango.
2.
A un amperímetro se le conecta una resistencia R 2 en paralelo para aumentarle
de un rango I 1 a un rango I . Demostrar que la resistencia equivalente del nuevo
amperímetro está dada por la ecuación.
R eq 
I  I1
I
 R2
3.
A un amperímetro se le aumenta el rango conectándole una resistencia de
derivación cuyo valor es apenas la cuarta parte de la resistencia interna del
amperímetro. Si el rango inicial era de 5 A , ¿cuál es el nuevo rango?
4.
A un amperímetro se le aumenta el rango conectándole una resistencia de
derivación cuyo valor es la novena parte de la resistencia interna del amperímetro. Si
la resistencia del nuevo amperímetro es de 0.18  , ¿Qué valor tiene la resistenci a de
derivación?
60

Voltímetro
Aumento el rango de un voltímetro. Considérese un voltímetro con un rango
v 1 y una resistencia interna R 1 , se desea aumentar el rango de este voltímetro de
modo que su aguja se deflecte toda la escala para una diferencia de potencial v 2 .
Aumentar el rango del voltímetro significa que si inicialmente la aguja se reflectaba
toda la escala pa ra medir una diferencia de potencial v 1 , ahora se deflectará toda la
escala para medir una diferencia de potencial v 2 , siendo v 2 un múltiplo de v 1 . En
consecuencia, para una di ferencia de potencial v 1 , la aguja se deflectará solo una
parte de la escala.
Si la corriente que pasa por el voltímetro se mantiene constante, el aumento en
la diferencia de potencial entre sus bornes solo se puede lograr con un aument o en su
resistencia interna, ya que si v 1  I R 1 , y v 2  I R 1  R 2 , entonces.

v2
v1

R1  R 2
1
R1

 v 2  v1
Por lo tanto, para cambiar de v 1 a v 2 se le debe conectar al voltímetro una gran
resistencia en serie, a la cual llamaremos R 2 .
Resistencia multiplicadora. Se le llama resistencia multiplicadora, R 2 , a la
resistencia que debe conectarse al voltímetro en serie para aumentar su rango. El
objetivo es deducir una ecuación que nos permita calcular la resistencia
multiplicadora para aumentar el rango del voltímetro.
v2
R2
v1
R1
Fig . 1
Para poder aumentar el rango del voltímetro de la
determinar el valor de la resistencia en serie R 2 .
 A
v 1  I R1
v 2  I R 1  R 2 
Dividiendo miembro a miembro
B  .
 A
v2
v1

R1  R 2
R1
61
B 
Fig . 1 , es necesario
Como R 1  R 2  R 1 
v2
v1
, entonces R 2  R 1 
 v2

R 2  R1 
 1
v

 1

v2
v1
 R 1 , factorizando.
1
Que es la ecuación buscada.
Factor de cambio de escala. Se le llama factor de cambio de escala al cociente
de rango de un voltímetro.
v2
C 
n
v1
La resistencia multiplicadora se puede calcular en función del factor de cambio
de escala, sustituyendo “ n ” de C  en la ecuación 1 .
R 2  R1 n  1
2
En donde.
R 1 : Es la resistencia interna del voltímetro inicial.
R 2 : Es la resistencia multiplicadora.
v 1 : Es rango inicial del voltímetro.
v 2 : Es nuevo rango del voltímetro.
n : Es factor de cambio de escala.
Resistencia interna equivalente. Se le llama resistencia interna equivalente a
la resistencia interna del nuevo amperímetro. El objetivo es deducir una ecuación
para calcular la resistencia interna del nuevo voltímetro . Como R 1 y R 2 están es
serie, se suman: R eq  R 1  R 2 , pero además: R eq  R 1 
R eq 
v2
v1
 R1
62
3
v2
v1
 R1  R1 .
Que es la ecuación buscada. Pero también la resistencia interna equivalente se
puede calcular en función del factor de cambio de escala sustituyendo “ n ” de C  en
la ecuación 3 .
R eq  n R1
4
Ejemplos.
1.
Un voltímetro tiene un rango de 1 v y una resistencia interna de 60  y se desea
aumentar su rango a 10 v .
a)
Calcular el valor de la resistencia multiplicadora.
Datos :
v1  1 v
v 2  10 v
R1  60 
 v2 
 10 v 
R 2  R1   1  60   
 1
v

1
v


1


b)
R 2  540 
Calcular la resistencia interna del nuevo voltímetro.
R eq 
v2
v1
 R1 
10 v
 60 
1v
R eq  600 
2.
Un voltímetro tiene una resistencia interna de 100  y se desea aumentar su
rango 5 veces su valor inicial.
a)
Calcular el valor de la resistencia multiplicadora.
Datos
R 1  100 
R 2  R1 n  1  100 5  1
n5
R 2  400 
b)
Calcular la resistencia interna del nuevo voltímetro.
R eq  n R1  5 100 
R eq  500 
63
Ejercicios.
1.
Un voltímetro tiene un rango de 1 v y para aumentarle el rango se le conecta
una resistencia que es nueve veces el valor de su resistencia interna, ¿cuál es el rango
del nuevo voltímetro?
2.
Para aumentar 5 veces el rango de un voltímetro se le conecta una resistencia
de 800  , ¿cuál era la resistencia interna del voltímetro?
64
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No. 8
Analizar las corrientes eléctricas inducidas debido a la fem inducida.
Inducción electromagnética

Ley de Inducción de Faraday
Concepto de inducción electr omagnética. La inducción electromagnética es
un fenómeno que se representa cuando un dispositivo, mediante una variación del
flujo magnético, induce a otro dispositivo una corriente eléctrica. El nombre de
inducción electromagnética es por el hecho de que una corriente
eléctrica es generada por un inductor.
Concepto de inducido e inductor. Para que exista inducción
electromagnética se requiere, básicamente, de dos dispositivos: el
que posee el campo magnético (que recibe el nombre de inductor) y
aquel donde se induce la corriente

 
eléctrica (que recibe el nombre de
I
inducido).
Inductor
El inducido generalmente es
una bobina y el inductor puede ser una bobina con
corriente o un imán. En la Fig . 1 cuando se cierra el
interruptor en la bobina inductora, aparece una
G Inducido
corriente inducida en la otra bobina, la cual es
Fig . 1
detectada por el galvanómetro. La corriente en el
inducido dura sólo un instante mientras se estabiliza la corriente en el inductor.
Si se abre el interruptor en el inductor , aparece nuevamente una corriente
inducida en la otra bobina, pero esta vez en sentido contrario, esto se pone de
manifiesto porque la aguja del galvanómetro se desvía al revés. La corriente en el
inducido dura sólo un instante mientras se anula por compl eto la corriente en el
inductor.
Estos resultados ponen de manifiesto que lo importante no es qué tan intensa
sea la corriente en el inductor, sino qué tan rápido se abre y se cierra el interruptor,
ya que la inducción magnética generada por el inductor or igina un flujo magnético en
la bobina del inducido, y es esta variación de flujo la que origina la corriente
inducida; esta variación de flujo se debe a un cambio de “ B ”, mismo que cambia con
la corriente.
S
N
65
En la Fig . 2 la corriente se induce en la espira
porque el flujo magnético está cambiando al moverse
el imán, si el imán se detiene, la corriente en la espira
desaparece, y si el imán se retira, en la espira aparece
una corriente en sentido puesto. Un efecto similar s e
produce si el imán permanece fijo y la espira es la que
se acerca o se aleja, ya que para inducir una corriente
en la espira, lo que importa es que haya movimiento
relativo entre el imán y la espira.
En algunos generadores comerciales , el campo
magnético permanece fijo, y el inducido gira con
velocidad angular constante. En ambos casos la
inducción se produce por una variación del flujo
magnético.
S
Imán
(inductor )
N
I
Espira
(inducido )
G
Fig . 2
Inducción electromagnética y el efecto motor. Puede interpretarse a la
inducción electromagnética como el inverso del efecto motor; al circular corriente en
una espira colocada en un campo magnético aparece un par de fuerzas que la obliga a
girar, es decir, la espira recibe energía eléctrica y entrega energía mecánica. Por otro
lado, si se hace girar la espira en el campo magnético, aparece una corriente inducida
en la espira, es decir, la espira recibe energía mecánica y entrega energía eléctrica.
Fem inducida. Si al cambiar el flujo magnético aparece una corriente en el
inducido, esto significa que en algún punto del circuito existe una fuente de fem
(algunas veces recibe el nombre de femi para hacer hincapié en que se trata de una
fem inducida). Esta fem inducida establece entre dos puntos cualesquiera del inducido
una diferencia de potencial “  ”.
Enunciado de la Ley de Inducción de Faraday. La fem inducida en un circuito es
igual al valor negativo de la rapidez de cambio del flujo magnético en el circuito. Su
expresión matemática es la siguiente.
 
d
dt
1
66
Como el flujo magnético se mide en webers y el tiempo en segundos, se deduce
del análisis de la ecuación 1 que las unidades deben ser volts, como era de de
esperarse ya que se trata de una fem inducida, la cual establece entre dos puntos del
circuito una diferencia de potencial.
De la ecuación 1 :
:
Es la fem inducida en el circuito.
d  : Es la variación de flujo magnético en el circ uito, puede leerse
diferencial de fí e interpretarse como la diferencial del flujo magnético
(la letra d es un operador diferencial que está actuando sobre  y de
ninguna manera lo está multiplicando).
d t : Es la variación del tiempo, puede leerse diferencial de t e interpretarse
como un intervalo de tiempo de duración infinitesimal (la letra d es un
operador diferencial que está actuando sobre t y de ninguna manera lo
está multiplicando).
d
, como conjunto puede leerse de fí en de t e
dt
interpretarse como la derivada del flujo magnético con respecto al tiempo.
Cuando se tiene el cociente
67

Ley de Lenz
Enunciado de la Ley de Lenz. El signo menos en la ecuación   
d
es la
dt
referencia a la Ley de Lenz que se enuncia a continuación.
La corriente inducida en un circuito aparece en un sentido tal que
se opone a la causa que la produce .
Interpretación de la Ley de Lenz.
S
x
N
S
N
Fig . 1
De la Fig . 1 , una espira con corriente presenta polaridad Norte -Sur. Cuando se
acerca el polo Norte de un imán, se induce una corriente I . La corriente circula de
abajo hacia arriba, saliendo por el corte superior y entrando por el corte inferior. La
corriente inducida genera un campo magnético cuyas líneas de inducción (según la
regla de la mano derecha) se dibujan en la Fig . 1 . Resulta que la cara más cercana al
imán se comporta como un polo norte y, en consecuencia, rechaza al imán, o sea, que
la corriente inducida aparece en un sentido tal que se opone a la causa que la
produce, sin embargo, si el imán se aleja, la corrie nte inducida aparece en sentido
opuesto y la cara más cercana al imán se comporta como un polo Sur, atrayendo al
imán.
68
La Ley de Lenz y el principio de conservación de la energía. Existe una
relación entre la Ley de Lenz y el principio de conservación de la energía, la cual
podemos analizar con dos aspectos.
1.
Como la corriente inducida aparece en un sentido tal que se opone a l a
causa que la produce, se debe hacer un trabajo para acercar el imán a
la bobina, este trabajo hecho contra la fuerza de repulsió n de los polos
magnéticos es energía que se disipa en forma de calor por el efecto
Joule.
2.
Si la corriente inducida apareciera en un sentido tal que no se opusiera
a la causa que la produce, la cara de la bobina más cercana al imán
presentaría polaridad in vertida y no se tendría que hacer ningún
trabajo para acercar el imán y, en consecuencia, el sistema bobina imán se convertiría en la fuente de energía que se disipa en forma de
calor por el efecto Joule, lo cual violaría el principio de la
conservación de la energía.
69

Fem de movimiento
Concepto de la fem de movimiento. Una fem que se induce al mover un
conductor a través de un campo magnético se llama fem de movimiento. El objetivo
es deducir una ecuación que nos permita calcular la fem inducida en una espira que
sale con velocidad constante “ v ” del seno de un campo magnético constante “ B ”.
S
S
N


N
S


N
N
S
Ecuación de la fem de movimiento.
x

















B
v
Fig . 1
En la Fig . 1 , la espira es sacada con velocidad constante del seno del cam po
magnético “ B ” que penetra perpendicular a la hoja de papel, “ x ” es la única cantidad
que está variando porque ésta disminuyendo “ y ”, por lo tanto.
dx
 v
dt
70
El flujo magnético que atraviesa la espira es.
 BA
Como A   x , entonces   B x , y aplicando la ley de inducción de Faraday.
 
d
d
dx
  B  x  B 
dt
dt
dt
  B v
1
Que es la ecuación buscada y donde:
 : Es la fem inducida en una espira que es sacada con velocidad “ v ” de un
campo magnético “ B ”.
v : Es la velocidad de la espira.
B : Es el campo magnético co nstante.
 : Es la longitud del segmento de la espira que corta con las líneas de
inducción.
Consideraciones complementarias. Como “  ” es la única parte de la espira
donde hay inducción, podría reemplazarse la espira por un alambre de longitud “  ” y
obtener, así, el mismo resultado ya que es el segmento “  ” donde se localiza la
fuerza de fem. Sobre la espira actúa una fuerza que se opone a que la espira sea
sacada del campo ma gnético; este efecto está previsto por la Ley de Lenz.
Ejemplo.
1.
Una espira cuadrada de 20 cm de lado sale con una velocidad constante de 4 ms
de un campo magnético constante de 0.5 T , calcular la fem indu cida.
1
  20 cm  2  10 m
Datos :
v  4 ms
  B  v  0.5 T  2 102 m 4 ms 
  0.4 v
71
B  0.5 T
Ejercicio.
1.
Una bobina tiene 400 espiras de 15 cm de lado y sale con velocidad constante de
3 ms de un campo magnético constante de 0.1 T , calcular la fem inducida.

El generador
Concepto y utilidad del generador. El generador es un dispositivo que
convierte la energía mecánica en energía eléctrica, su funcionamiento se basa en la
inducción electromagnética debida al movimiento relativo ent re un campo magnético
y una bobina que gira en el interior del campo. Si la fem inducida es alterna, al
generador se le llama alternador, en cambio, si es directa, al generador se le llama
dínamo.
Estructura del generador. El generador consta de tres parte s esenciales:
Rotor, Estator y Colectores. El rotor contiene a la bobina del inducido y gira con
velocidad angular constante en el seno del campo magnético en forma tal que el eje
de la bobina es perpendicular al campo. El estator contiene las piezas polar es y las
bobinas excitantes con los que se genera un campo magnético constante y los
colectores , que pueden ser dos anillos concéntricos o un anillo partido en dos,
dependiendo de sí se trata de un alternador o de una dínamo.
En el caso del alternador , los anillos concéntricos y aislados entre sí, giran con
el rotor. Cada anillo constituye, en esencia, uno de los polos del alternador y
conectan con el circuito exterior por medio de escobillas apoyadas contra ellos. En un
instante dado, la posición del induc ido es tal que la corriente alcanza su máximo
valor; al continuar girando, la corriente inducida se hace cero e inmediatamente
cambia su polaridad, aumentando hasta alcanzar su máximo valor negativo, después
volverá a disminuir su intensidad hasta hacerse cero y crecerá hasta alcanzar de
nuevo su máximo valor. Es debido a estas alternancias (cambio de polaridad) que a
esta corriente se le llama alterna y de ahí el nombre de alternador.
Un electroimá n genera un fuerte campo
electromag nético entre sus polos
Al girar el alambre en el interior del campo
electromag nético se genera un flujo
de electrones una corriente eléctrica 
Al dar media vuelta completa a la bobina,
el flujo de electrones se invierte obteniendo
una corriente alterna
72
En el caso de la dínamo, el colector es
un anillo partido en dos mitades y cada mitad
está conectada a una terminal del inducido y
a una terminal del circuito exterior. Des pués
de que la corriente alcanza su máximo valor,
disminuye hasta hacerse cero, y en el
instante en que se invierte el sentido de la
corriente, se intercambian las conexiones y
la corriente aumenta nuevamente en sentido
positivo.
El
generador
electromecáni co
o
dínamo que transforma la energía mecánica
en energía eléctrica.
La dinamo fue el
primer generador eléctrico apto para uso
industrial y emplea principios electromagnéticos para convertir la energía de rotación
mecánica en corriente continua.
En la Fig . 1 se muestra el esquema básico de un generador (no se muestra el
inductor).  A: Alternador, donde los conectores son dos anillos concéntricos y B :
Dínamo, donde el colector es un anillo partido en dos.
Eje de
rotación
Inducido
Colectores
B
B
Terminales
Terminales
 A
Fig . 1
B 
Colector
Ecuación de la fem inducida en un alternador. Consideremos una espira que
gira en el seno de un campo magnético constante que es producido por el inductor. El
área de la espira es representada por un vector “ A ” normal al plano de la espira. Este
vector gira con velocidad angular constante alrededor del eje de rotación, pero su
magnitud (que es el área de la espira) si es constante. La posición de la espira con
respecto al campo magnético define un flujo magnético dado por la ecuación.
  B  A  B A cos 
Donde  es el ángulo entre los vectores A y B .
73
Como la espira gira con velocidad angular constante, el ángulo  varía
uniformemente con el tiempo (  es el desplazamiento angular). De acuerdo con la
Ley de Faraday, la fem inducida en la espira es.
 ' 
d
d
d
d
  B A cos    B A cos    B A  sen  
dt
dt
dt
dt
 '  B A sen 
Pero por definición, tenemos que
d
dt
d
  (velocidad angular).
dt
 '  B A  sen 

  , y por lo tanto,    t , pero   2 f , así que
t
  2 f t , por lo que la fem inducida en la espira es.
Además, si  es constante,
 ' B A  sen 2 f t 
Y para una bobina de “ N ” espiras tenemos que.
  N B A  sen 2  f t 
1
Donde:
 : Es la fem inducida en el alternador.
N : Es el número de espiras que tiene la bobina del inducido.
B : Es la magnitud de la inducción magnética que produce el inductor.
A : Es el área de la espira.
 : Es la velocidad angular con que gira el rotor (inducido).
f : Es la frecuencia con que gira el rotor (inducido).
t : Es un tiempo cualquiera.
74
Gráfica de la fem inducida en una dínamo. Analizando la ecuación 1 ,
deducimos que la fem inducida en un alternador es una selenoide, esto es debido a la
estructura del colector. En la dínamo, en cambio, debido a que el colector es un a nillo
partido en dos, en el instante en que se invierte el sentido y la fem se intercambian
las conexiones al circuito exterior y la fem aumenta nuevamente en sentido positivo.
La fem inducida por la dínamo de la Fig . 1 B se muestra en la Fig . 2 , donde la línea
punteada es la parte de la selenoide que correspondería a una fem alterna.

t
Fig . 2
Si el inducido de la dínamo consta de un gran número de bobi nas conectadas en
serie, se eliminan prácticamente las fluctuaciones, de manera que la gráfica de la fem
es virtualmente una línea recta, a esta fem inducida en la dínamo se le llama continua
o directa porque, a diferencia de la fem alterna, nunca cambia s u polaridad y, en
consecuencia, siempre aparece en el mismo sentido.

t
Fig . 3
75

Valores máximo, medio y eficaz
Gráfica de la fem inducida en un alternador.
 max

 min
1
2


3
2

2
5
2

3 
Valor máximo de la fem inducida en un alternador. La fem inducida en un
alternador es:   N B A  sen 2 f t , donde el valor máximo ocurre cuando:
n
para “ n ” entero impar, porque sen 2 f t   1 y, por lo tanto.
2 f t 
2
 max  N B A
2
Así que la ecuación 1 se puede escribir.
   max sen 2  f t 
3
Gráfica de la corriente inducida en un alternador (corriente alterna).

I
I
76

Como la corriente inducida en el alternador es alterna, también tiene forma
senoidal, a un cierto tiempo “ t ” le corresponde un cierto ángulo “  ” y la corriente se
puede expresar como.
I  I max sen 
4
Donde:
Es la corriente instantánea.
I:
I max : Es el valor máximo de la corriente.
:
Es el desplazamiento angular medido en radianes en un instante dado.
La corriente y la fem inducida tienen la mima frecuencia, pero están desfasados
un ángulo “  ”. En un instante dado, el desplazamiento angular de la fem es “  t ”,
mientras que el desplazamiento angular de la corriente es    t   .
Definición del valor medio de una corriente alterna. Se define el valor medio
de una corriente alterna como la media algebraica de sus valores instantáneos.
Im 
1
I 1  I 2    I n 
n
Y en términos de sumatoria.
Im 
1 n
Ik
n k 1
k  ésima corrient e
instantánea y “ n ” es el número de valores instantáneos considerados en un intervalo
de tiempo.
Siendo “ I m ” el valor medio de corriente, “ I k ” es la
77
Ecuación del valor medio de una corriente alterna. El objetivo es deduci r
una ecuación que nos permita calcular el valor medio de una corriente alterna.
Consideremos un intervalo de medio período, porque en un período completo, el valor
medio de la corriente es cero.
I
I max
Im
Fig . 3

0

El desplazamiento angular en medio periodo es “  ” (medio giro). La corriente
“ I m ” es un valor constante, el área del rectángulo de la Fig . 3 es.
A Im
 Im 
A

Pero el área del rectángulo es equivalente al área bajo la curva de la selenoide.


0
0
A   I d    I max sen  d 
Entonces.
Im 
1


0
I max sen  d  
Im 
1

2


1
0

I max  sen  d  
I max
I max   cos   0

5
Que es la ecuación buscada.
De manera similar se puede expresar el valor medio de una fem inducida.
m 
2

 max
6
El valor medio de una fem inducida se define como la media algebraica de sus
valores instantáneos.
78
Definición del valor eficaz de una corriente alterna. Se define al valor eficaz
de una corriente alterna como el valor de una corriente constante que en una misma
resistencia y en u n mismo tiempo disipa la misma cantidad de calor.
Ecuación del valor eficaz de una corriente alterna. En un periodo “ T ”, la
energía disipada en la resistencia es.
 
W  Ie
2
 A
RT
Siendo I e la corriente eficaz . La energía disipada en forma de calor por una
corriente alterna en periodo “ T ” es.
dw
dt
P
 dw P dt
Pero I  I max sen   t  , entonces.
P  I 2 R  I max sen 2  t  R
2
Por lo tanto.
d w  I max sen 2  t  R d t
2
Integrando.
w   I max sen 2  t  R d t  I max R  sen 2  t  d t
T
2
T
2
0
0


w  I max R 12 t  41 sen 2 t 
2
T
0

2
B 
w  12 I max R T
2
Pero como A  B , entonces.
I e R T  12 I max R T
2
2
2
Ie 
2
Ie 
1
2
I max R T
RT
1
2
I max
 12 I max
2
7
Que es la ecuación buscada. De manera similar.
e 
1
 max
2
79

 I max R 12 T  41 sen 2 t 
8
Ejemplo.
La tensión en dos bornes de un alternador medida con un voltímetro es de
220 v , calcular el valor máximo de la fem.
Dato :
 e  220 v
e 
  max  2  e  2 220 v 
1
 max
2
 max  311.13 v
Ejercicio.
Calcular el valor medio de una corriente alterna si su valor eficaz es de 10 A .

El transformador
Concepto y utilidad del transformador. El transformador es un dispositivo
que sirve para aumentar o disminuir diferencias de potencial y, asimismo, para
disminuir o aumentar intensidades de corriente. Su funcionamiento se basa en la
inducción electromagnética.
Estructura del transformador.
G
C. A.
Primario
v1
v2
Secundario
80
El transformador se compone, básicamente, de dos bobinas llamadas primario
y secundario, y aisladas eléctricamente entre sí pero devanadas sobre el mismo
núcleo de hierro. La bobina por donde llega la corriente al transformador es el
primario y la bobina por donde sale la corriente es el secundario. La corriente alterna
que alimenta al prima rio produce un campo magnético alterno que origina un campo
magnético alterno. Este flujo magnético atraviesa la bobina del secundario e induce
en él una fem alterna.
Transformador real y transformador ideal. En un transformador real, part e
del flujo que atraviesa el núcleo, sale del primario.
En un transformador real existen pérdidas.
 Pérdidas del cobre. Es la energía disipada en forma de calor por el efecto
Joule a través de las bobinas primaria y secundaria.
 Pérdidas del núcleo. Es la energía disipada po r la histéresis del núcleo y
las corrientes parásitas (de Foucault) en el núcleo. Estas pérdidas se
reducen usando un material con ciclo de histéresis estrecho y
fabricando el núcleo laminado.
Debido a estas pérdidas, la potencia de salida es menor que la potencia de
entrada.
En un transformador ideal se considera que no hay pérdidas de flujo, no ha y
pérdidas de cobre ni pérdidas del núcleo, y por lo tanto, la potencia de entrada es
igual a la potencia de salida, esto es con la finalidad de facilitar algunos cálculos.
Ecuaciones del transformador ideal . El objetivo es deducir tres ecuaciones
conocidas como ecuaciones del transformador . Si la diferencia de potencial aplicada
a los bornes del primario es alterna, produce un flujo magnético que cambio con el
tiempo, esta diferencia de potencial se puede ex presar en términos de la Ley de
Inducción de Faraday como.
 1  N 1
d
dt
 A
Siendo N 1 el número de vueltas y  1 es la diferencia de potencial, ambos en el
primario. Debido a la inducción electromagnética, apare ce en el secundario una fem
inducida dada por la ecuación.
d
B 
 2  N 2
dt
Siendo N 2 el número de vueltas y  2 es la diferencia de potencial, ambos en el
secundario. Dividiendo las ecuaciones entre sí, tenemos .
 1 N1

2 N2
1
81
Que es la primera ecuación buscada.
Con un transformador ideal la potencia de entrada es igual a la de salida
P1  P2 , y como P   i , entonces  1 i1   2 i2 , por lo tanto.
 1 i1

 2 i2
2
Que es la segunda ecuación buscada.
Como
1 N1
, entonces.

2 N2
i1
i2

N1
3
N2
Que es la tercera ecuación buscada.
De las tres ecuaciones anteriores:
 1 : Es la diferencia de potencial en el primario.
 2 : Es la diferencia de potencial en el secundario.
N 1 : Es el número de vueltas en el primario.
N 2 : Es el número de vueltas en el secundario.
i 1 : Es la corriente en el primario, corriente de entrada.
i 2 : Es la corriente en el secundario, corriente de salida.
Transformador elevador. Un transformador es elevador cuando la diferencia
de potencial en el secundario es mayor que en el primario v 2  v 1 , entonces.
v2
v1
Por la ecuación 1 .
v2
v1

1
N2
N1
1
Entonces.
N 2  N1
82
Por lo tanto, para que un transformador sea elevador, se requiere que el
secundario tenga más vueltas que el primario.
Como N 2  N 1 , entonces
N1
N
 1 , y por la ecuación 3 , tenemos que
2
v1
v2

N1
N2
1,
entonces.
i 2  i1
O sea, en un transformador elevador, la corriente de salida es menor que la de
entrada.
Transformador reductor. Un transformador será reductor cuando la diferencia
v2
 1, y
de potencial en el secundario sea menor que en el primario v 2  v 1 , entonces
v1
por la ecuación 1 , tenemos.
v2
v1

N2
N1
1
Entonces.
N 2  N1
Para que un transformador sea reductor, se requiere que el secundario tenga
N1
 1 , y por la ecuación
menos vueltas que el primario. Como N 2  N 1 , entonces
N2
3 , tenemos.
i 2  i1
En un transformador reductor, la corriente de salida es mayor que la de
entrada.
El calentamiento por el efecto Joule provoca grandes pérdidas de energía
eléctrica en transporte a grandes distancias, este problema se resuelve mediante el
uso de transformadores elevadores que dan potenciales con los cuales se obtienen
tensiones muy elev adas y corrientes muy bajas, reduciéndose así al mínimo las
pérdidas por calentamiento, i 2 R , en la línea de transporte. Por otra parte, en los
lugares de consumo, se requieren tensiones relativamente bajas que se obtienen
mediante el uso de transformadores reductores.
83
Ejemplo.
1.
El primario de un transformador tiene 800 espiras y la corriente de entrada es
0.5 A , el secundario tiene 200 espiras , ¿cuál e la corriente de salida?
Datos :
N 1  800
i2
i1

N1
N2
N 1  200
 i2 
i1  0.5 A
i1 N 1

N2
0.5 A 800
200
i2  2 A
2.
a)
Un transformador tiene 500 vueltas en el primario, v 1  120 v y v 2  24 v .
¿Cuántas vueltas hay en el secundario?
Datos :
N 1  500
v2
v1

N2
N1
v1  120 v
 N2 
v 2  24 v
v2 N1
v1

24 v  500
120
N 2  100 vueltas
b)
Si la corriente en el secundario es de 2 A , ¿cuál será la corriente en el
primario?
i1
i2

N2
N1
 i1 
84
N2
N1
i2 
100
2 A
500
i1  0.4 A
3.
Un transformador conectado a una línea de 100 v tiene una potencia de salida de
20 w , la bobina del primario tiene 200 vueltas y la del secundario tiene 1 000 vueltas ,
¿cuál es la corriente de salida?
Datos :
P2  20 w
v1  100 v
N 1  200
P2  v 2 i 2
v2
v1

N2
N1
 i2 
 i2 
 v2 
N2
N1
N 2  1 000
P2
v2
 v1 
N 2 v1
N1
P2
P2 N 1
20 w 200


N 2 v1 N 2 v1 1 000 100 v 
N1
i 2  0.04 A
Ejercicio.
1.
El primario de un transformador tiene 600 espiras con una tensión de 400 v , la
bobina del secundario tiene 30 espiras y la corriente de salida es de 0.1 A , ¿cuál es la
potencia de entrada?
85
Inductancia

Generalidades
Concepto de inductancia. Si por las espiras de una bobina circula una

corriente “ I ”, esta corriente genera una inducción magnética “ B ” y las líneas de
inducción que atraviesan el área de sección transversal de las espiras definen un flujo
magnético “  ”. Si la bobina no esta montada sobre un núcleo de materia
ferromagnético (tiene núcleo de aire), el valor del flujo magnético depende
directamente de la corriente, o sea que.
    I 

 

Y esta relación entre  e I es lineal. Por esta razón, cualquier variación del

flujo magnético solo puede ser producida por una variación de la corriente I . Un
circuito en el cual se puede generar un campo magnético que dependa linealmente de
la corriente se dic e que es inductiva y, por lo tanto, posee una propiedad llamada
inductancia.
La inductancia “ L ” de una bobina es una constante que se define como la razón
de la variación de flujo a la variación de corriente.
Primera ecuación que defin e la inductancia. La definición de la inductancia
se puede expresar en símbolos como.
L
d
 A

dI
Que es la primera ecuación que define la inductancia y donde:
L : Es la inductancia de la bobina.
 : Es el flujo magnético de la bobina.

I : Es la corriente en la bobina.
d : Es el operador diferencial, d  indica que es un elemento diferencial de

flujo y d I indica que es un elemento d iferencial de corriente.
En conjunto, la expresión
d
se interpreta como la derivada del flujo con

dI
respecto a la corriente, lo que significa que el flujo cambia porque cambia la
corriente.
86
Segunda ecuación que define a la inductancia. Como al cambiar la corriente
en la bobina, también cambia el flujo magnético y se induce una fem en la bobina
misma, es por esta razón que se le llama fem autoinducida, la cual obedece a la ley de
inducción de Faraday como cualquier otra fem inducida, así tenemos.
L
d d t d d t
d
, pero

 
di dt dt di
dt
Entonces.
L

di dt
B 
Que es la segunda ecuación que define a la inductancia y donde:
L : Es la inductancia de la bobina.
i : Es la corriente en la bobina.
 : Es la fem autoinducida en la bobina al cambiar la corriente en la bobina
misma.
d : Es el operador diferencial, d i indica que es un elemento diferencial de
corriente y d t indica que es un elemento diferencial de tiempo.
di
se interpreta como la derivada de la corriente con
dt
respecto al tiempo, o sea, es la rapidez con que cambia la corriente en la bobina, el
di
signo negativo indica que “  ” y
son de signo contrario, de acuerdo a la Ley de
dt
Lenz, ya que “ L ” siempre es positiva, así, en base a la ecuación B  podemos definir
a la inductancia de una bobina como la razón de la fem autoinducida a la rapidez de
cambio de la corriente en la bobina misma.
En conjunto, la expresión
Encadenamiento de flujo. Para una bobina apretada, un selenoide o un toroide,
se le llama encadenamiento de fluj o al producto “ N  ”, en donde “  ” es el flujo
magnético producido por cada vuelta y “ N ” es el número de vueltas. Por lo tanto, la
inductancia total de una bobina de “ N ” espiras, por la ecuación  A , es.
L
d N
di
Separando variables e integrando.
1
Li  N 
87
Unidades de la inductancia. Despejando “ L ” de la ecuación 1 , tenemos.
L
N
i
weber
,
ampere
combinación que se conoce como henry y se representa con el símbolo “ H ”. La
inductancia de una bobina es de 1 H si el flujo magnético en la bobina es de 1 wb
cuando por ella pasa una corriente de 1 A . Los submúltiplos del henry son.
Y si vemos que las unidades de la inductancia en el S. I. son
microhenry  H  10 6 H
milihenry  mH  10 3 H
La inductancia como una constante. Cuando la bobina de un toroide tiene
núcleo de aire, su flujo magnético es.
  o N A
i
  

Puede verse que el flujo magnético depende de la geometría de la bobina y de
la intensidad de la corriente, con la condición de que no haya materiales magnéticos
en la vecindad, de modo que cualquier variación de flujo magnético solo puede ser
producida por una variación de la corriente, esto es.
d d di

dt
di dt
Pero.
d  o N A

di

Por lo tanto,
d
es una constante.
di
Si el núcleo del toroide fuera de un mate rial ferromagnético, el flujo sería.
 N A
i
  

Y como “  ” no es una constante, el flujo magnético ya no sería linealmente
d
dependiente de la corriente y, en consecuencia,
ya no sería una constante, po r eso
di
se pone la condición de que no haya materiales magnéticos en la vecindad para que la
inductancia de una bobina sea constante.
88

Cálculo de la inductancia
Ecuación de la inductancia en un selenoide. Nuestro objetivo es deducir una
ecuación que nos perm ita calcular la inductancia de un selenoide, por lo cual, la
inducción de tal selenoide será.
o Ni
B

Y el flujo magnético.

o N I A

Pero como.
LI  N
Entonces
LI  N
o N I A


o N2 I A

Y simplificando “ I ”, tendremos.
L
o N 2 A

1
Que es la ecuación buscada y donde:
L : Es la inducción del selenoide.
N : Es el número de espiras del selenoide.
A : Es el área de la sección transversal del selenoide.
:
Es la longitud del selenoide.
 o : Es la permeabilidad del aire , 4 10 7 Hm .
Si de la ecuación 1 despejamos  o :
o 
L
N2A
Podemos deducir que sus unidades serán:
serán:
H
.
m
89
henry metro henry

, y en símbolo
metro
metro 2
Ecuación de la inductancia en un toroide. Esta ecuación es la misma que l a
de un selenoide, o sea.
L
o N 2 A
1

Y si consideramos que   2 r , la ecuación 1 se puede escribir.
L
o N 2 A
2 r
2
Donde:
L : Es la inducción del toroide.
N : Es el número de espiras del toroide.
A : Es el área de la sección transversal del toroide.
:
Es la longitud del toroide.
r:
Es radio del toroide.
 o : Es la permeabilidad del aire , 4 10 7 Hm .
Ecuación de la inductancia en una bobina plana. El objetivo es deducir una
ecuación que nos permita calcular la inductancia de una bobina circular plana. La
inducción magnética en el centro de la bobina es.
B
o Ni
2R
Y el flujo magnético es.
o Ni A
  BS 
Pero como L i  N  , entonces L i 
L
2R
o N 2i A
2R
o N 2 A
2R
90
, y cancelando “ i ”, tendremos.
3
Que es la ecuación buscada y donde:
L:
Es la inducción de la bobina.
N : Es el número de espiras.
A : Es el área de la sección transversal de la bobina.
R : Es radio de la espira A   R 2 .
 o : Es la permeabilidad del aire, 4 10 7 Hm .
Ejemplos.
1.
Calcular la inductancia de una bobina de 500 espiras por las cuales circula una
corriente de 2.5 A , creando un flujo magnético de 1.4 10 4 wb .
Datos :
N  500
i  2.5 A
  1.4  104 wb
L i  N 
 L
N   500  1.4  104 wb
i
2.5 A


L  2.8  102 H
2.
Un selenoide tiene una inductancia de 1.2 10 4 H , ¿cuál será la inductancia si se
comprime la bobina y la longitud del selenoide se reduce en un 10 % ?
Datos :
4
L1  1.2  10 H
L1 
 o N 22 A
1
L2 
L 2  0.9 L 1
o N2A
2

o N2A
0.9 1
1.2  104 H
L2 
0.9
L 2  1.33 104 H
91
2
1   o N A L 1



0.9   1  0.9
3.
La bobina de un toroide tiene una sección transversal de 10 cm 2 y 600 espiras
por las que pasa una corriente de 0.2 A , el radio medio del toroide es de 12 cm ,
calcular la inductancia de la bobina.
Datos :
3
A  10 cm  10 m
2
2
N  600
i  0.2 A
r  12 cm  12  102 m
 o N 2 A 4   107 Hm  600 2 103 m 2 
L

2 r
2  12  10 2 m
L  6  104 H
Ejercicios.
1.
Un toroide tiene 1 000 espiras , ¿cuántas espiras deberá tener para que su
inductancia se reduzca a la cuarta parte?
2.
Calcular la inductancia de una bobina circular plana que tiene 20 espiras de 4 cm
de radio.

Energía almacenada en una bobina
La energía almacenada en una bobina es igual al trabajo hecho para establecer
un campo magnético en torno a la bobina.
Ecuaciones de la energía almacenada en una bo bina. Nuestro objetivo es
deducir dos ecuaciones que nos permitirán calcular la energía almacenada en el
campo magnético de la bobina se calcula a partir del trabajo hecho para establecer la
corriente en la bobina desde un valor cero hasta un valor “ i ”.
v
La diferencia de potencial entre los extremos de la bobina es.
V L
92
di
dt
La potencia suministrada a la bobina es
P  V i  Li
d i dW
, en donde

dt
dt
d W  L i d i , de modo que la energía total se obtiene integrando.
W   d W   Li d i
1
W  12 L i 2
Que es la primera ecuación buscada.
Como L i  N  , entonces L 
N
N  2
, por lo tanto, W  12 
i , reacomodando,
i
 i 
tendremos.
2
W  12 N  i
Que es la segunda ecuación buscada y donde:
W : Es la energía almacenada en la bobina.
L : Es la inductancia de la bobina.
 : Es el flujo magnético de la bobina.
i:
Es la corriente que circula por la bobina.
N : Es número de espiras de a bobina.
Ejemplos.
1.
En una bobina cuya inductancia es de 1.5 10 3 H pasa una corriente de 0.4 A .
Calcular la energía almacenada en la bobina.
Datos :
3
L  1.5  10 H
W  12 L i 2 
1
2
i  0.4 A
1.5 10
3
H  0.4 A
W  1.2  104 J
93
2
2.
En una bobina de 500 espiras por la que pasa una corriente de 0.5 A se forma un
flujo magnético de 6 10 5 wb , calcular la energía almacenada en la bobina.
Datos :
N  500
  6  10 5 wb
i  0.5 A
W  12  i N 
1
2
6 10
5
wb 0.5 A500
W  7.5  103 J
Ejercicios.
1.
Un toroide tiene 600 espiras con una sección transversal de 15 cm 2 por las que
pasa una corriente de 0.4 A , el radio medio del toroide mide 15 cm , calcular la
energía almacenada en el toroide.
2.
La energía que se almacena en una bobina es de 8 10 4 J , calcular la energía
que se almacena en la bobina si la corriente se reduce a la mitad.

Inductancia mutua
Concepto de inductancia mutua. Cuando se tiene dos bobinas adyacentes, las
variaciones de corriente en cualquiera de las dos no son independientes de las
variaciones de corriente en la otra bobina, ya que están ligadas por fenómenos de
inducción y autoind ucción. Así como cada bobina tiene su propia inductancia, las
bobinas están relacionadas por una inductancia que es común a las dos y que recibe el
nombre de inductancia mutua. La inductancia mutua se representa con la letra “ M ” y
su unidad también es el henry.
Factor de acoplamiento. Como hay un flujo ligado a la bobina 1, y un flujo
ligado a la bobina 2, resulta que no todo el flujo de una bobina reacciona sobre la
otra, ambas bobinas reaccionan bajo la acción del flujo mutuo. El fluj o en cualquiera
de las dos bobinas se iguala al flujo mutuo por medio de un número “ k ” llamado
factor de acoplamiento, siendo k  1 , o sea,  m  k  1  k  2 , entonces.
N1  N 2  N
Ecuaciones que definen la inductancia mutua. Se puede definir la inductanci a
mutua como la razón de la variación del flujo en la bobina 1 a la variación de la
corriente en la bobina 2.
d 1
M 1
d i2
94
O también se puede definir como la razón de var iación del flujo en la bobina 2
a la variación de la corriente en la bobina 1.
M 2
d2
d i1
En virtud de que  m  k  1  k  2 , entonces M 
dm
d i1
o M
dm
d i2
.
Ecuaciones de la inductancia mutua de dos bobinas acopla das. Nuestro
objetivo es deducir dos ecuaciones que nos permitan calcular la inductancia mutua.
Consideremos dos selenoides a los que llamaremos 1 y 2, la inducción magnética
producida por la bobina 1, y el flujo magnético en la bobina 2, son.
B1 
 o N 1 i1
 2  B1 N 2 A  B1 

 o N 1 i1

N2 A
Reacomodando.
2 
o N1 2 A

 i1
Y como  m  k  2 , entonces.
m 
Pero como M 
dm
d i1

k o N1

M
2
k o N1
2

A
 i1
A d i1

, por lo tanto.
d i1
k  o N1 N 2 A

1
Que es la primera ecuación buscada.
Fácilmente se puede verificar que si consideramos a la inducción magnética
producida por la bobina 2, se llega a la misma ecuación 1 , por lo que la inductancia
en cada bobina será.
 o N 12 A
 o N 22 A
L1 
L2 


Y si multiplicamos miembro a miembro, tendremos.
L1 L 2 
 o 2 N 12 N 2 2 A 2
2
95
Multiplicando por “ k 2 ”, obtendremos.
k 2 o N1 N 2 A2
2
k L1 L 2 
2
2
2
2
O sea, que M 2  k 2 L1 L 2 , por lo tanto.
2
M  k L1 L 2
Que es la segunda ecuación buscada y donde:
M : Es la inductancia mutua.
N 1 : Es el número de espiras en la bobina 1.
N 2 : Es el número de espiras en la bobina 2.
A:
:
k:
L1 :
Es el área de la sección trans versal de las espiras.
Es la longitud del selenoide.
Es el factor de acoplamiento.
Es la inducción de la bobina 1.
L 2 : Es la inducción de la bobina 2.
 o : Es la permeabilidad del aire , 4 10 7 Hm .
Ejemplos.
1.
Se tienen dos selenoides adyacentes de 15 cm de largo y área de sección
transversal de 15 cm 2 con 200 y 600 espiras, respectivamente, si el factor de
acoplamiento es 0.8 .
a)
Calcular la inductancia mutua.
Datos :
2
A  15 cm 2  15  10  4 m 2
  15 cm  15  10 m
N 2  600
M
k o N1 N 2 A


N 1  200
k  0.8
0.8 4  107 Hm 200 600 15 104 m2 
15  102 m
M  1.2  103 H
96
b)
Calcular L 1 y L 2 .
Como L 1
o N 1 2 A

y L2
o N 2 2 A

, entonces.
o A
L1


N1
2

L2
N2
2
Por lo tanto.
L1
200
2

L2
600 2
De donde.
M  k L1 L 2  k L1 9L1   k 9L1  3kL1
2
 L1 
M 1.2 10 3 H

3k
3 0.8
L1  5 10 4 H
Como L 2  9L1 , entonces.

L 2  9 5 10 4 H

L 2  4.5 103 H
Ejercicios.
1.
Calcular la inductancia mutua de dos selenoides acoplad os de 9 cm de largo con
200 y 400 vueltas, respectivamente, el área de sección transversal es de 10 cm 2 y el
factor de acoplamiento vale 0.9 .
2.
Dos selenoides de
300 y
900 espiras están igualados por un factor de
acoplamiento de 0.8 a una inductancia mutua de 2.4 10 4 H , calcular sus inductancias.
97
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No.9
Com probar la s analogías de circuitos m agnéticos con circuitos el éctricos .
El circuito magnético y la Ley de Ohm

La Ley de Ohm del magnetismo
Concepto de circuito magnético. Se le da el nombre de
circuito magnético a un dispositivo que debido a la corriente
eléctrica, produce un flujo magnético, el cual está confinado a una
trayectoria cerrada. Como ejemplo de circuitos magnéticos son el
toroide y el transformador.
El circuito magnético y su analogía con el circuito
eléctrico. En el circuito eléctrico de la Fig . 1 , la corriente recorre
una trayectoria cerrada, y en circuito magnético de la Fig . 2 , las
líneas de inducción también recorren una trayectoria cerrada.
I

R
Fig . 1
Fig . 2
En el circuito eléctrico de la Fig . 1 .
De donde I 

R
 IR
 A

A
B 

1
, y si.
R
Entonces.
I

A
El flujo en el circuito magnético de la Fig . 2 es.

NI A

98
Reacomodando.

2
NI

A
Comparando las ecuaciones 1 y 2 , vemos que su estructura es muy similar y
donde.
  corresponde a I
 N I corresponde a 



corresponde a
A
A
En el circuito de la Fig . 1 , la corriente eléctrica se debe a la presencia de la fem,
y en el circuito de la Fig . 2 , el flujo magnético existe por la corriente “ I ” que circula
por las “ N ” espiras de la bobina. Un factor que se opone al paso de la corriente en el

circuito eléctrico es el cociente
, y de igual modo se puede inferir que el cociente
A

se opone a la resistencia del flujo en el circuito magnético.
A
Concepto de fuerza magnetomotriz  f m m . En el circuito eléctrico, la fuerza
electromotriz “  ” es la causa por la que existe corriente en el circuito; de manera
similar, en el circuito magnético es la corriente que pasa por cada una de las espiras
la causa que hace posible la existencia del flujo magnético. Por esta razón, a la
corriente total que circula por la bobina del circuito se le llama fuerza
magnetomotriz, la cual se representa con la letra “  ”.
Ecuación de la fmm. La corriente total que circula por la bobina del circuito
magnético es la corriente que pasa po r cada espira multiplicada por el número de
espiras, por lo tanto, la fuerza magnetomotriz será.
3
 N I
Donde:
 : Es la fuerza electromotriz del circuito magnético.
I : Es la corriente en las espiras.
N : Es el número de espiras que tiene la bobina del circuito.
99
Unidades de la fmm. Analizando la ecuación 3 , deducimos que las unidades
de la fuerza magnetomotriz son.
Ampere  vuelta
En símbolos.
Av

representa la resistencia en el
A
circuito eléctrico la cual se puede expresar como la razón de la fuerza electromotriz
  a la corriente (despejándola de la ecuación 1 ). De manera análoga, la expresión

representa la resistencia magnética en el circuito de la Fig . 2 , la cual recibe el
A
nombre de reluctancia . En el circuito magnético, la reluctancia s e puede expresar
como la razón de fuerza magnetomotriz  al flujo magnético (despejándola de la
ecuación 2  ) y se representa con la letra “  ”.
Concepto de reluctancia. La expresión
Ecuación de la reluctancia. Atendiendo a la estructura de la ecuación
comparando con la ecuación B  , la reluctancia debe ser.


A
2
y
4
En donde.
 : Es la reluctancia en el circuito magnético.
:
Es la longitud media del circuito.
A : Es el área de la sección transversal del núcleo.
 o : Es la permeabilidad del núcleo.
Unidades de la reluctancia. Despejando en la ecuación 2 y combinando con
la ecuación 4 , tenemos.

NI


A 
Como las unidades de N I son Ampere  vuelta , y las de  son weber , deducimos
que las unidades de la reluctancia son.
Ampere  vuelta
weber
En símbolos.
Av
wb
100
Factores de los que depende la reluctancia. Analizando la ecuación
deducimos que la reluctancia depende de dos factores.
4 ,

 La geometría del circuito   .
 A
 La permeabilidad magnética del núcleo.
Ecuación del circuito magnético. Si en la ecuación 2 , sustituimos  y
por  , obtendremos  

A

, o bien.

5

Que es la ecuación del circuito magnético.
La Ley de Ohm en el circuito magnético. La fem, la corriente y la resistencia
en el circuito eléctrico de la Fig . 1 están relacionados por la Ley de Ohm.
5

La fem, el flujo magnético y la reluctancia en el circuito magnético de la Fig , 2
están relacionados por la ecuación del circuito magnético.
5
 R
La estructura de la ecuación 5 es similar a la de la ecuación  A , por esta
razón, a la ecuación del circuito magnético también se le conoce como la Ley de Ohm
del magnetismo.
101
Carácter no lineal de la Ley de Ohm del magnetismo. La resistencia en el

circuito eléctrico es R 
, y como “  ” es constante, “ R ” también debe serlo
A
(dentro de un rango moderado de corriente). Si.
 A
 IR
Y “ R ” es constante, la corriente “ I ” debe ser linealmente dependiente de “  ”.

En el caso de la reluctancia es diferente porque  
, pero recordando la curva de
A
magnetización.

H
Vemos que “  ” no es constante y, por lo tanto, la reluctancia no puede ser
constante, es por esta razón que la ecuación     , “  ” no es linealmente
dependiente de “  ”. Esta es la diferencia fundamental entre la Ley de Ohm de la
electricidad y la Ley de Ohm del magnetismo, la no linealidad de ésta última.
Permeancia. La permeancia se representa con la letra “ P ” y es el inverso de la
1

reluctancia, si  
y P  , entonces.

A
P
A

6
Siendo “  ” la permeabilidad del núcleo, “ A ” es el área de la sección
transversal del núcleo y “  ” es la longitud del circuito magnético. Si las unidades de
wb
1
la reluctancia son
, y como P  , y    R , entonces la ecuación del circuito
A

magnético en función de la permeancia se puede escribir.


5 '
P
102
Entrehierro. Al corte seccional efectuado en el núcleo de un toroide se le da el
nombre de entrehierro. Si inicialmente la reluctancia del núcleo era  o , al hacer el
entrehierro aparecen dos reluctancias en serie: la que
corresponde al núcleo y la que corre sponde al
entrehierro.
v
Entrehierr o
Si la longitud del núcleo es “  ”, entonces  o 
entrehierro es “  1 ”, entonces  1 
1
o A
2 

, y si la longitud del
A
, y la reluctancia del núcleo cortado es:
1
A
.
Nuestro objetivo es deducir una ecuación que nos permita calcular la
reluctancia equivalente del núcleo con el entrehierro.
Aunque las líneas de inducción se deforman levemente en el entrehierro, el
flujo magnético en ambas partes e s el mismo, o sea    1   2 , y si el embobinado esta
devanado sobre cada parte, la fmm será N I  N 1 I  N 2 I , o sea que    1   2 ,
entonces      1    2 , y simplificando, tendremos.
  1   2
Que es la ecuación buscada y donde:
 : Es la reluctancia equivalente.
 1 : Es la reluctancia del entrehierro.
 2 : Es la reluctancia del núcleo cortado.
103
7
La reluctancia equivalente es.

Si  o 
1
o A

1
A

1r
A

1
A
1 r 1

A


   1   r  1
A


, entonces se cumple que    1  r  1   , y por lo tanto    o .
A
Conclusión: Al hacer un entrehierro al núcleo de un toroide, aumenta l a
reluctancia.
Ejemplos.
1.
El núcleo de un toroide tiene una longitud media de 60 cm , una sección
transversal de 20 cm 2 y una permeabilidad de 5 10 4
wb
Am
, la bobina del toroide tiene
1 800 espiras por las que pasa una corriente de 0.4 A . Calcular.
2.
a)
La fuerza electromotriz.
b)
La reluctancia del circuito.
c)
El flujo magnético.
Datos :
2
  60 cm  60  10 m
N  1 800
  5  104
I  0.4 A
Solución.
a)
  N I  1 800  0.4 A  720 A  v
b)


60 10 2 m

 6 10 5

4

4
2
wb
 A 5 10 A m 20 10 m
c)

 720 A  v

 1.2 10 3 wb
 6 105 Awb v


A  20 cm 2  20  10 4 m 2

104
Av
wb
wb
Am
3.
El núcleo de un toroide tiene un radio de 10 cm , un área de sección transversal
de 15 cm 2 y una permeabilidad relativa de 400 , la bobina del toroide tiene 1 500
espiras por las que pasa una corriente de 0.5 A
a)
Calcular la fmm.
b)
Calcular la permeancia.
c)
Calcular el flujo magnético.
Datos :
2
r  10 cm  10  10 m
N  1 500
A  15 cm 2  15  10  4 m 2
 r  400
I  0.5 A
Solución.
a)
  N I  1 500  0.5 A  750 A  v
b)
 r  o A 400 4  10 7 Awbm  15 10 4 m 2 
P


 1.2 10 6
2

2 r
2  10 10 m
c)
   P  750 A  v  1.2 10 6
A
wb
Av
  9 10
4
wb
105
wb
Av
4.
Un toroide tiene una longitud media de 60 cm , una permeabilidad relativa de
500 y un área de sección transversal de 20 cm 2 .
a)
Calcular la reluctancia del núcleo.
b)
Al núcleo se le hace un entrehierro de 1 mm de largo, ¿cuánto vale la reluctancia
del entrehierro?
c)
Calcular la reluctancia equivalente.
d)
¿En qué porcentaje aumento la reluctancia del núcleo?
Datos :
1
 1  599 mm  599  10 3 m
  60 cm  6  10 m
 r  500
A  20 cm 2  2  103 m
 2  1 mm  10 3 m
Solución.
a)
o 
b)
2 
c)
1 

r o A
2
o A


6 10 1 m
500 4 10
4 10
1
r o A

7 wb
Am
 2 10 m
3
10 3 m
7 wb
Am
 2 10 m
3
o
100 %


x
 3.98 105


 x

Av
wb
 3.98 105

A
wb
Av
wb
599 10 3 m
 4.77 10 5
7 wb
3
500 4 10 A m 2 10 m
   1   2  4.77 105
d)
 4.44 10 5
5
100 %  100 % 8.75 10

A
o
4.77 105 wb
Av
wb
Av
wb
Av
wb
 8.75 105
Av
wb
  183.43%
Ejercicios.
1.
Cuando un toroide tiene núcleo de aire , su permeancia es de 3 10 9
wb
A
, y si al
mismo toroide se le monta en un núcleo de acero, su permeancia cambia a 1.2 10 6
calcular la permeabilidad relativa del núcleo.
2.
wb
A
,
El núcleo de un toroide tiene un diámetro interior de 11 cm y un diámetro
exterior de 13 cm con una permeabilidad de 6 10 4 Awb m . El embobinado tiene 10
vueltas de alambre por cada centímetro de longitud, calcular.
a)
La fuerza magnetomotriz necesaria para establecer un flujo magnético de
1.5 10 6 wb .
b)
La reluctancia del circuito.
c)
La corriente en las espiras.
106
3.
El núcleo de un toroide tiene una longitud media de 60 cm , una permeabilidad
relativa de 400 y su reluctancia es  o . Al núcleo se le hace un entrehierro, ¿de qué
largo deberá ser el entrehierro para que la reluctancia e quivalente sea de 2  o ?

Comparación de los circuitos eléctrico y magnético
Corriente eléctrica y flujo eléctrico. La corriente en el circuito eléctrico
recorre una trayectoria cerrada y regresa al mismo ponto, en cambio, el flujo en el
circuito está confinado a una trayectoria cerrada.
Fem y fmm. En el circuito eléctrico la fuerza electromotriz ( fem) es la causa
por la que existe corriente en el circuito, y en el circuito magnético, la fuerza
magnetomotriz (fmm) es la causa que hace posibl e la existencia del flujo magnético.
Resistencia y reluctancia. En el circuito eléctrico, la resistencia se opone al
paso de la corriente, y en el circuito magnético, la reluctancia se opone a la
existencia del flujo. La resistencia se puede expresar como la razón de la fem a la
corriente en el circuito eléctrico, y la reluctancia se expresa como la razón de la fmm
al flujo en el circuito magnético.
Factores de los que dependen la resistencia y la reluctancia. La resistencia

en el circuito eléctrico depende de la geometría del conductor   y de la
 A

conductividad, y la reluctancia depende de la geometría del circuito magnético   y
 A
de la permeabilidad.
La Ley de Ohm en los circuitos eléctricos y magnéticos. En el circuito
eléctrico, la fem, la corriente y la resistencia están relacionadas por la Ley de Ohm,
  I R , y en el circuito magnético, la fmm, el flujo magnético y la reluctancia están
relacionados por la Ley de Ohm del magnetismo,    .
Resistencia y reluctancia en serie. La resistencia equivalente de dos
resistencias en serie es R  R 1  R 2 y es mayor que la mayor de las resistencias. La
reluctancia equivalente de dos reluctancias en serie es    1   2 , que es mayor que
la reluctancia mayor.
107
COMPETENCIA PARTICULAR 2.
Analizar, com prender y construir los conceptos, principios y leyes fundam entales de las
ondas, para explicar y predecir los fenóm enos que se producen en el m ovimiento
ondulatorio com o son: propiedades de energía, reflexión, difracción y refracción de tal
m anera que aplique estos conocim ientos en el área tecnológica y en su vida cotidiana.
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No.1
Conocer m ediante investigación docu m ental y experiencias recreativas el m ovim iento
ondulatorio y sus apli caciones .
UNIDAD # 2 DEL PROGRAMA: ONDAS
Movimiento ondulatorio

Ondas
Concepto de movimiento ondulatorio. El movimiento ondulatorio (periódico,
vibratorio o de vaivén) es el que realiza una partícula que es apartada de su posición
de equilibrio y luego soltada, la partícula se mueve de adelante hacia atrás sobre una
trayectoria fija que es recorrida una y otra vez a intervalos regulares de tiempo.
Concepto de onda. Una onda es la perturb ación de un medio físico que, como
consecuencia de una perturbación inicial, se propaga por el mismo en forma de
oscilaciones periódicas.
Ondas mecánicas y ondas electromagnéticas. La diferencia entre las ondas
mecánicas y las ondas electromagnéticas es qu e las electromagnéticas se pueden
propagar en el vacío, y las mecánicas necesitan de un medio material para
propagarse; las ondas mecánicas no se pueden propagar en el vacío.
Para que una onda mecánica se pueda propagar en un medio material, éste debe
reunir dos propiedades: Inercia y elasticidad. La elasticidad da lugar a las fuerzas
restauradoras de cualquier partícula del medio que sea desplazada de su posición de
equilibrio; es la inercia la que nos dice cómo responderá esta partícula (que ha s ido
desplazada de su posición de equilibrio) a esas fuerzas restauradoras.
108
Concepto de ciclo. Una onda cumple un ciclo cuando la partícula que vibra
vuelve a ocupar la misma posición que tenía antes de transcurrir un periodo.
Concepto de periodo. El periodo es el tiempo que tarda una partícula en
efectuar una vibración completa. Observando el paso de las ondas desde un punto de
referencia, el periodo es el tiempo necesario para que pase una onda completa. El
periodo se mide en segundos.
Concepto de frecuen cia. Observando el paso de la onda desde un punto de
referencia (fijo), la frecuencia es el número de ondas que pasan en la unidad de
tiempo. En el S. I., la unidad de frecuencia es el hertz (Hz) y es el inverso del
periodo y, a su vez, el periodo es el in verso de la frecuencia.
Concepto de longitud de onda. La longitud de onda es la distancia que ha y
entre dos crestas sucesivas o entre dos puntos de la onda que se encuentren en la
misma fase. La longitud de onda se mide en metros.
Concepto de amplitud de o nda. La amplitud de una onda es igual a la
amplitud de la vibración de una partícula del medio donde se propaga la onda, la
amplitud es el desplazamiento máximo de la partícula con respecto de su posición de
equilibrio. En el S. I., la amplitud se mide en metros.
Concepto de fase. La fase se puede expresar en función del tiempo,
definiéndose como la fracción del periodo transcurrida desde que la partícula pasó
por su posición de equilibrio moviéndose en sentido positivo. La fase se puede
expresar también en función del desplazamiento angular, considerando que 360 º
constituyen un ciclo completo y que para recorrer 360 º se ocupa un periodo “ T ”.
Longitud de onda
Amplitud
Fig . 1
Dos partículas que oscilan con igual frecuencia (o igual periodo) están en fas e
cuando en un instante dado ocupan posiciones idénticas en su respectivo ciclo. Si el
ciclo de una de ellas se inicia con retaso con respecto a la otra, se dice que están
desfasadas, eso hace que sus ondas no coincidan y que en los círculos de referencia
difiera la posición de las partículas por un ángulo “  ”.
109

90 º
270 º
180 º
360 º
Fig . 2
Ecuación que define la velocidad de propagación de una onda. La velocidad
de propagación de una onda se calcula con la ecuación.
1
v f
Donde:
v : Es la velocidad de la onda medida en
m
s
.
 : Es la longitud de onda medida en metros.
f : Es la frecuencia de la onda medida en hertz


ciclos
segundo
Ejemplo.
1.
Una onda con una frecuencia de 100 Hz tiene una longitud de onda de 11 m ,
calcular la velocidad de propagación de la onda.
Datos :
f  100 Hz
  11 m
v  1100 ms
v   f  11 m100 Hz
110

Ondas transversales y ondas longitudinales
Concepto de onda transversal. En un onda transversal, las partículas del
medio vibran perpendicularmente a la dirección en que se propaga la onda misma,
como puede verse en la Fig . 3
Onda transversal
v
Fig . 3
Ejemplos de ondas transversales. Un ejemplo lo constituye la onda que se
propaga a lo largo de una cuerda sometida a tensión cuando en uno de sus extremos se
le aplica un impulso. La onda avanza a lo largo de la cuerda, pero las partículas que
forman la cuerda vibran en una dirección perpendicular a ésta. Otro ejemplo lo
constituyen la ondas luminosas, en las cuales, por ser electromagnéticas, la
perturbación que se propaga no produce un movimiento de partículas material es, sino
un campo electromagnético que cambia, pero tanto el campo eléctrico como el
magnético son perpendiculares a la dirección de propagación de la onda y, por lo
tanto, ésta es transversal.
111
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No.2
Determ inar la velocidad de propagación de las ondas .
Ecuación de la velocidad de onda en una cuerda. Nuestro objetivo es deducir
una ecuación que nos permita calcular la velocidad con que una onda se propaga a lo
largo de una cuerda. Dicha velocidad depende de la elasticidad de la cuerda y de su
inercia. La elasticidad se determina sometiendo a la cuerda a una tensión, a lo que la
cuerda responde con una fuerza restauradora “ F ”. La inercia se determina por la
densidad lineal de una masa (masa por unidad de longitud).
Si la fuerza se mide en Newtons y la densidad lineal de masa en
deben combinarse de modo que se obtengan
Kilogramos
,
metro
metros
, que son las unidades de la
segundo
velocidad, entonces.
N

Kg m
Kg m
s2 
Kg m
Kg m
m
s2

Kg
Kg m 2
m2 m
s2


Kg
s
s
Este análisis nos permite postular una proporcionalidad.
F
v

Y si introducimos la unidad como constante de proporcionalidad, tendremos:
v
1
F

Que es la ecuación buscada y donde:
v : Es la velocidad con que se transmite la onda por la cuerda.
F : Es la fuerza aplicada a la cuerda para producir la onda.
 : Es la densidad lineal de masa (masa por unidad e longitud).
Concepto de onda longitudinal. En una onda longitudinal, las partículas del
medio vibran en la misma dirección en que se propaga la onda, como puede verse en
la Fig . 4 .
v
Fig . 4
112
Ejemplos de ondas longitudinales. Un ejemplo lo constituye la onda que se
propaga a lo largo de un resorte vertical sometido a una tensión y es sometido a una
oscilación vertical hacia arriba y hacia abajo por uno de su s extremos. A lo largo del
resorte avanza una onda longitudinal y las espiras oscilan hacia arriba y hacia abajo
en la misma dirección en que se propaga. Otro ejemplo lo constituyen las ondas
sonoras en las cuales las partículas del medio (sólido, líquido o gaseoso) que
transmiten la perturbación, oscilan en la dirección en que se propaga la misma.
Ecuación del periodo de vibración de un resorte. Nuestro objetivo es deducir
una ecuación que nos permita calcular el periodo de vibración de un resorte que
oscila con un peso suspendido en uno de sus extremos.
2
A
y
0
A
1
F  k y
113
El resorte ha sido sacado de su posición de equilibrio en 0 y llevado hasta la
posición 1 , al soltarlo la fuerza recuperadora “  k y ” lo obliga a comprimirse y el
cuerpo suspendido en el extremo sube; el cuerpo no se detiene en 0 , sino que
continua la compresión del resorte hasta llegar a 2 , de donde volverá a extenderse.
Despreciando las pérdi das de energía por el calentamiento del resorte y por la
fricción, podemos suponer que el cuerpo volverá a la posición 1 , donde comenzará a
contraerse comenzando de nuevo el ciclo. El tiempo que tarda el cuerpo en realizar un
ciclo completo se llama periodo.
En los puntos 1 y 2 la energía potencial elástica del resorte es máxima, y la
energía cinética es cero, mientras que en el punto 0 la energía cinética es máxima y
la energía potencial es cero.
En
y
la velocidad del cuerpo es “ v ” y su energía cinética es
que su energía potencial es
tenemos que.
1
2
1
2
m v 2 , mientras
k y 2 . Del principio de conservación de la energía
0  12 k A 2  12 m v 2  12 k y 2
Despejando “ v ”, tenemos.
v
Y recordando que v 
k
m
A2  y 2
dy
, entonces.
dt
dy
k

dt
m
A2  y 2
Podemos calcular “ y ” en función de “ t ” separando las variables y efectuando
la integral definida.
dy
A2  y 2

k
dt
m

A
0
dy
A2  y 2

k
m

1
T
4
0
dt
Se toman los límites en virtud de que podemos proponer que en y  0 , t  0 ,
cuando el cuerpo va de 0 a 2 , el desplazamiento efectuado es “ A ”, y el tiempo
que tarda en efectuar este recorrido es un cuarto de periodo, o sea, 14 T .
114
Resolviendo y evalu ando la integral.
1
T
A
 k 4
k
 y
 A
0
arc sen    
t   arc sen   - arc sen   
m
 A 0  m  0
 A
 A
 arc sen 1 - arc sen 0  14 T
 
1

2
0
T  2
k 1
   14 T
m 2
14 T  0 
k
m
2
m
k
Que es la ecuación buscada y donde:
T : Es el periodo de oscilación del resorte.
m : Es la masa del cuerpo suspendido en el extremo del resorte.
k : Es la constante de restitución del resorte.
Ejemplos.
1.
Calcular la velocidad con que una onda se propaga a lo largo de una cuerda de
3 m de largo y que tiene suspendida una masa de 500 g si se le aplica una fuerza de
24 N .
Datos :
3m
m  500 g  0.5 Kg
v
F


F

m

F  24 N
v  12
24 N
0.5 Kg
3m
m
s
2.
Calcular el periodo de vibración de un resorte que oscila con un cuerpo
suspendido en su extremo inferior y cuya masa es de 100 g si la constante de
restitución del resorte es de 2.5 Nm
Datos :
m  100 g  0.1 Kg
k  2.5 Nm
T  1.26 s
m
0.1 Kg
T  2
 2
k
2.5 Nm
115
Ejercicios.
1.
Un cable que tiene una masa de 3 Kg y una longitud de 30 m y está sometido
por sus extremos a una tensión de 40 N . Si se peroduce una onda en uno de sus
extremos, ¿cuánto tiempo tardará la onda en llegar al otro extremo?
2.
Un cuerpo que pesa 20 N se suspende de un resorte y lo estira 5 cm a partir de
su posición de equilibrio. Si se quita e l cuerpo y en su lugar se cuelga un bloque con
una masa de 1 Kg , el resorte comienza a oscilar, ¿cuál es el periodo de vibración del
resorte?
116
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No.3
Identificar las características objetivas y subje tivas del sonido, así com o la velocidad de
propagación del sonido en diferentes medios y su variación con la tem peratura;
características del audiogram a hum ano, nivel de intensidad sonora y el efecto Doppler.
Acústica

Sonido
Concepto de sonido. Se le llama sonido a una perturbación que al producirse
en un medio elástico se propaga por el medio hasta llegar al oído donde se produce la
sensación de audibilidad.
Audición. A la función que desempeña el sentido del oído se le llama audición,
y para que exista audición se requieren tres elementos:
1.
Fuente de ondas sonoras.
2.
Un medio material que posea elasticidad e inercia que capture las
vibraciones de la fuente para que éstas se transmitan a través de él en
forma de ondas longitudinales.
3.
Un receptor que reciba las ondas sonoras.
Límites de audición. Las ondas sonoras se reducen a los límites de frecuencia
que pueden estimular el oído humano para producir en el cerebro la sensación
acústica, estos límites son desde aproximadamente 20 Hz a cerca de 20 000 Hz . Si la
frecuencia de una onda mecánica longitudinal es menor al límite inferior, se le llama
onda infrasónica, y si es mayor al límite superior se le llamará onda ultrasónia.
117
Fuentes de sonido. Se entiende por fuente de sonido a una fuente emisora de
ondas sonoras. Las fuentes de sonido se clasificarán en tres tipos:
1.
Cuerdas en vibración, por ejemplo el violín y las cuerdas humanas.
2.
Columnas de aire en vibración, por ejemplo el órgano y la trom peta.
3.
Placas y membranas en vibración, por ejemplo el tambor y el magnavoz.
Reflexión de una onda sonora. Es el cambio de dirección que experimentan las
ondas sonoras al icidir sobre una superficie reflejante (al reflejarse el sonido
continua propagándos e por el mismo medio, pero en otra dirección).
Refracción de una onda sonora. Es el cambio de dirección que experimentan
las ondas sonoras al atravesar una superficie refractante, continuando su propagación
en el mismo o en otro medio.
Resonancia acústica. Es la propiedad que tiene un cuerpo capaz de vibrar en
virtud de la cual, cuando el cuerpo es sometido a una serie periódica de impulsos,
cuya frecuencia sea igual a la de una de sus frecuencias naturales, vibra con una
amplitud relativamente grande. Si l a onda que se produce al vibrar es una onda
sonora, al entrar el cuerpo vibrante en resonancia aumenta la intensidad acústica del
sonido, a este efecto se le llama resonancia acústica.
Consideremos el caso de una cuerda sujeta por sus extremos y sometida a una
una fuerza “ F ”. Si se le aplica un impulso, la cuerda empezará a oscilar,
produciéndose una onda que se propaga a lo largo de la cuerda. En los extremos de la
cuerda se localizan los nodos, y entre estos se puede formar uno, vario s o ningún
nodo, esto depende de que entre los extremos de la cuerda se forme una onda o
varias, o solamente una semilongitud de onda (media onda).
118
Entre dos nodos adyacentes se forma una semilongitud de onda, por lo tanto, no
importa cuántos nodos aparezcan entre los extremos de la cuerda, siempre se formará
un número entero de semilongitudes de onda. Si la longitud de onda es “  ”, la
separación entre dos nodos es “ 12  ”.
a 
b 
c 
Fig . 1
De acuerdo con la Fig . 1 , en la cuerda tensa a la que se le da un impulso puede
formarse una onda completa localizándose tres nodos a  , pueden formarse tres
semilongitudes de onda loca lizándose cuatro nodos b  , o puede formarse solamente
una semilongitud de onda localizándose únicamente dos nodos que corresponden a los
extemos de la cuerda c  .
Si “  ” es la longitud de la cuerda y “ n ” es el número de semilongitudes de
onda, entonces.
2
1
 
2 n  
n
Y como v 
F

  f , entonces
f 
1
F


, y sustituyéndo el valor de “  ”
tenemos que.
f 
n
2
F

Para n  1, 2, 3, 
A estas frecuencias se le llama frecuencias naturales.
119

Características del sonido
Características objetivas y subjetivas del sonido. Dichas características son.
OBJETIVAS
Intensidad
Frecuencia
Forma de la onda
SUBJETIVAS
Sonoridad
Tono
Timbre
Las características objetivas son puramente físicas y son la causa real que
determina las características subjetivas del sonido, en cambio las caractrísticas
subjetivas son la forma como el cerebro interpreta las características ob jetivas del
sonido al ser estimulado el sentido del oído. Podría decirse que las caracterísicas
objetivas son la causa que origina a las características subjetivas o viceversa. En
cambio, las características subjetivas son consecuencia de las objetivas.
Concepto de tono. El tono es la característica del sonido por la cual el oído le
asigna un lugar en la escala musical. Como el tono es una característica subjetiva del
sonido, su magnitud depende de la capacidad sensorial del individuo que lo percibe,
por lo tanto, el tono dependerá de la frecuencia; si la frecuencia es muy baja, el
sonido es grave y a medida que ésta aumenta el sonido se hace más agudo. La
frecuencia es una característica objetiva del sonido porque es una medida física del
número de vibraciones por segundo.
Concepto de timbre. El timbre es la propiedad del sonido por la cual el oído
puede determinar qué objeto lo produce, por lo tanto, el timbre depende de la forma
de la onda.
Cuando un cuerpo vibra, puede hacerlo con muchas frecuencias, en el caso de
una onda sonora que produce una cuerda en vibración, la frecuencia se expresa por:
f 
n
2
F
Para n  1, 2, 3, 

120
1 F
y recibe el nombre de frecuencia
2 
fundamental, para los subsecuentes valores de “ n ” la frecuencia se puede expresar en
función de f 1 : f 2  2 f 1 , f 3  3 f 1 , etc. Todas estas frecuencias constituyen una serie de
Para n  1 , la frecuencia será
f 
armónico, siendo f 1 el primer armónico, 2 f 1 el segundo armónico, etc. Es debido a
esta variedad de frecuencias que al vibrar un cuerpo no produce un solo sonido, sino
varios sonidos; el sonido principal y los sonidos que corresponden a los armónicos,
los cuales son más débiles. En términos de ondas sonoras podemos decir que al vibrar
un cuerpo no produce una sola onda sonora, sino varias ondas que se combinan entre
sí dando lugar a una onda compleja cuya forma determinará el timbre.
Flujo de energía acústica. El flujo de energía acústica es la energía que l a
onda sonora transmite por el medio (aire, por ejemplo) en la unidad de tiempo, en
dW
otras palabras, es la potencia de la onda sonora,  
, cuya unidad es
dt
Joule
 watt y su símbolo es “ w ”.
segundo
Intensidad acústica. Es el flujo de energía acústica por unidad de superficie
normal a la dirección de propagación de la onda. Puede expresarse también como la
potencia por unidad de superficie normal a la dirección de propagación de la onda, o
bien como la energía transmitid a por la onda por unidad de superficie normal.

, siendo “  ” el flujo de energía
S
acústica y “ S ” el área normal. Sus unidades pueden expresarse de dos mane ras:
La intensidad acústica se expresa como J 

watt
w
 2
metro cuadrado m

Joule
J

segundo metro cuadrado s  m 2
La intensidad acústica es proporcional al cuadrado de la frecuencia y al
cuadrado de la amplitud, se puede calcular con la ecuación.
J  2 2  v f 2 A2
1
Donde:
J : Es la intensidad acústica.
 : Es la densidad del medio (aire, por ejemplo) medida en
v : Es la velocidad del sonido en el medio.
f : Es la frecuencia de la onda sonora medida en hertz
A : Es la amplitud de la onda medida en metros.
121

Kg
m3

ciclos
segundo
Nivel de intensidad acústica. Es la relación logarítmica entre una intensidad
acústica de referencia y una intensidad acústica cualquiera, su unidad es el decibel,
con síbolo “ db ” y se puede calcular con la ecuación.
I  10 Log
2
J
Jo
Donde:
Log : Es el logaritmo en base diez.
Jo :
Corresponde
aproximadamente
al
sonido
más
débil
que
puede
escucharse y su valor es 10 12 mW2
En principio se había definido al bel (en honor a Alexander Graham Bell) como
unidad del nivel de intensidad acústica, pero esta un idad es muy grande y por eso se
adoptó el decibel, que corresponde a la décima parte del bel : 1 bel  10 decibeles .
Si la intensidad acústica de una onda sonora es J o , su nivel de intensidad
acústica es cero, y si la intensidad acústica es de 1 mw2 , su nivel de intensidad acústica
es de 120 db .
Sonoridad.
La
sonoridad
es
la
característica del sonido mediante la cual el oído
humano distingue un sonido débil de uno fuerte.
La sonoridad es una característica subjetiva del
sonido porque no puede medirse con aparatos y
su estimación solo depende de la capacidad
auditiva de la persona que escuha el sonido. Si la
intensidad de un sonido es peq ueña, el nivel de
intensidad acústica también es pequeño, en
términos de sonoridad, el sonido es débil. Si por
el contrario, la intensidad del sonido es grande, el nivel de intensidad acústica
también es grande, y en términos de sonoridad se dice que el so nido es fuerte.
Ejemplos.
1.
El oído humano puede percibir intensidades como la de un tren en movimiento
cuya intensidad es de 10 3 mw2 , y si el mínimo de intensidad audible es de 10 12 mw2 ,
determinar el nivel de intensidad acústica del tren en movimiento.
Datos :
103 mw2
J
I  10 Log
 10 Log 12 w  10 Log 109
3 w
12 w
J  10 m 2
J o  10 m 2
Jo
10 m 2
I  90 db
122
2.
Se tiene un sonido de intensidad acústica J 2 mayor que la intensidad acústica
J 1 correspondiente a otro sonido más débil. Demostrar que el nivel de intensidad
acústica de estos dos sonidos está dado por la ecuación I  10 Log
J2
, donde “ I ” es la
J1
diferencia del nivel de los dos sonidos.
I  I 2  I 1  10 Log
J2
Jo

J2
J1 
 10  Log
 Log

Jo
Jo
J o 

J1
 10 Log

 
 10 Log J 2  Log J o  Log J 1  Log J o

 10 Log J 2  Log J o  Log J 1  Log J o
  10  Log J

J2
J2
 10  Log
  10 Log
J 1 
J1

3.
 
2

 Log J 1 
I  10 Log
J2
J1
Calcular la intensidad acústica de un sonido de 20 db más alto que otro cuya
intensidad acústica es de 10 8
w
cm 2
.
Datos :
J 1  108 cmw 2  104
I  20 db
I  10 Log
w
m2
J2 ?
J2
2  Log J 2   4  Log J 2  4
Log J 2  2 mw2
J1
10
20  10 Log
Log J 2
 102
J
10
2
4 w
m2
2  Log J 2  Log 104
w
m2
j 2  0.01 mw2
w
m2
Ejercicios.
1.
La diferencia entre los niveles de intensidad acústica de dos sonidos es de
10 db . El sonido más alto tiene una intensidad acústica de 10 4 mw2 , ¿cuál es la
intensidad acústica del sonido más bajo?
2.
Un ruido de 70 db proviene de la calle y penetra por el hueco de una ventana
que tiene una superficie de 0.9 m 2 , ¿cuál es la potencia de la onda que pasa por la
ventana?
123

Velocidad del sonido
Ecuación de la velocidad del sonido en los fluídos. Nuestro objetivo es
deducir una ecuación que nos permita calcular la velocidad del sonido en los fluídos.
Cilindro
PA
Fluido en reposo
Pistón
Fig. 1
La Fig . 1 muestra un fluido en reposo confinado en un cilindro y ejerciendo una
presión “ P ” sobre la cara interna del pistón, el cual se mantiene en equilibrio por la
F
acción de una fu erza “ F ”. Como por definición P  , entonces F  P A .
A
vt
v' t
P   P  A
Fig. 2
v'
v'
Fluido en reposo
Onda sonora
Fluido en movimiento
Para un tiempo t o  0 el pistón se pone en movimiento por la acción de un
impulso “ F ”. La fuerza neta que actúa sobre el pistón es.
F  P   P A  P A   P A
De la Segunda Ley de Newton, sabemos que F 
 t  t  t o , pero p o  0 para t o  0 , por lo tanto, F 
 p  A 
p
, de modo que.
t
p   p  At
p
, siendo  p  p  p 0 y
t
p
, y como F   P  A , entonces
t
a
Expresión en la cual “ P ” es la variación de la presión en el fluido y “ p ” es la
cantidad de movimiento lineal del fluido en movimiento. Ahora debemos encontrar
una expresión para “ P ” y para “ p ”.
Al ponerse el pistón en movimiento, produce una onda sonora (que es
longitudinal) que se propaga por el fluido con una velocidad “ v ”, mientras que el
pistón se mueve con una velocidad “ v ' ”, y con esa misma velocidad se mueve el
fluido que ha sido afectado por la perturbación. Obsérvese en la Fig . 2 que la parte
del fluido que ha sido afectado por la perturbación (a la izquierda de la onda) se
mueve con la misma velocidad del pistón “ v ' ”, mientras que la parte del fluido que
no ha sido afectado por la perturbación (a la derecha de la onda) se encuentra en
reposo.
124
En un intervalo de tiempo “ t ”, el pistón ha recorrido una distancia d ' v ' t , y en
el mismo intervalo la onda sonora ha recorrido una distancia d  v t . En este intervalo
de tiempo “ t ”, el volumen del fluido puest o en movimiento es.
V  d A  vt A
Este volumen inicial ha sido disminuido un volumen.
V '  d ' A  v 't A
Donde “ A ” es el área de la sección transversal del cilindro, entonces el
volumen en que se ha reducido el fluido es.
 v  v 't A
Pero el módulo de compresibilidad “ B ” de un fluido está definido como.
B
P V P

V
V
v
Sustituyendo los valores de “ V ” y de “  V ”, tenemos.
B
V  P v t A  P v  P


V
v 't A
v'
Despejando “  P ” obtendremos.
P 
v'B
v
b
m
, de donde
v
m   v , y sustituyendo el valor de “ v ”, m   v t A, además la cantidad de movimiento
del fluido en movimiento es p  m v ' , o sea que.
Por otra parte, se define a la densidad de un fluido como  
p   v t Av '
c
Sustituyendo “  P ” de b  y “ p ” de c  en la ecuación a  , obtendremos.
v ' B  A t   v t Av '
v
Despejando “ v ” y simplificando, se obtiene la ecuación.
v
1
B

Que es la ecuación buscada.
125
Ecuación de la velocidad del sonido en los sólidos. Nuestro objetivo es
deducir una ecuación que nos permita calcular la velocidad del sonido en los sólidos.
En el caso de un cuerpo sólido, la velocidad de una onda sonora que se propaga a
través de él al ser golpeado por un objeto depende de dos factores:
 La elasticidad del medio.
 De su inercia.
Como el medio es un sólido, en lugar de usar el módulo de compresibilidad se
usa el Módulo de Young Y  que es la característica que determina la elasticidad y
Newton
sus unidades son
, la inercia se determina por la densidad del medio,
metro cuadrado
Kilogramo
con unidades
, estas unidades se deben combinar para obtener las
metro cúbico
unidades de la velocidad.
N
m2 
Kg
m3
3
Nm

Kg m 2
Kg m
m
m2 m
s2


Kg
s
s2
Nm

Kg
Por lo tanto, podemos proponer que “ v 
Y

” por lo que es necesario introducir
una constante de proporcionalidad para obtener la igualdad. Teórica y
experimentalmente se ha demostrado que esta constante de proporcionalidad es la
unidad, por lo tanto, tendremos que.
2
Y
v

Que es la ecuación buscada y donde:
v : Es la velocidad del sonido en
 : Es la densidad del medio en
m
s
.
Kg
.
m3
B : Es el módulo de compresibilidad del fluido en
Y : Es el módulo de Young del sólido en
126
N
m2
.
N
m2
.
Velocidad del sonido y la temperatura. La velocidad del sonido puede variar
con la temperatura. En los líquidos y en los sólidos esta variación es muy pequeña y
se puede considerar despreciable, pero en los gases es considerable. Nuestro objetivo
es deducir una ecuación que nos permita calcula r la variación de la velocidad del
sonido en función de la variación de la temperatura. Las ondas sonoras que se
transmiten a través de un gas producen en éste comprensiones y refracciones. Cuando
un gas se comprime, aumenta su temperatura y cuando se dila ta disminuye su
temperatura, sin embargo, las comprensiones y refracciones que producen las ondas al
propagarse se suceden tan rápidamente que sus moléculas no alcanzan a ganar ni a
perder energía considerándose, entonces, que la propagación de las ondas s onoras a
través de los gases es adiabática. En un gas a temperatura constante, el módulo de
compresibilidad adiabático “ B ” es “  ”, el módulo de compresibilidad isotérmico
“ P ”, siendo “  ”.

calor específico del gas a presión constante
calor específico del gas a volumen constante
Para el aire   1.4 , por lo tanto, se cumple que.
B
v

P


1'
La ecuación general de los gases establece que.
P   RT
a
Ecuación en la que “ P ” es la presión del gas, “  ” es su densidad, “ T ” su
temperatura y “ R ” es la constante universal de los gases. Sustituyendo “ P ” de a  en
la ecuación 1' , obtenemos.
v   RT
2 '
Ahora valoremos “ v ” para T 1 y T 2 .
v 1   R T1
v 2   RT 2
Dividiendo miembro a miembro y simplificando:
v2
v1

T2
T1
v2
v1

 RT2
 R T1
3
Que es la ecuación buscada y donde:
v 1 : Es la velocidad del sonido a la temperatura T 1 .
v 2 : Es la velocidad del sonido a la temperatura T 2 . Si T1  0 º C , se debe
convertir a º K : 0 º C  273 º K
127
Ejemplos.
1.
Calcular la velocidad del sonido en el cobre, el módulo de Young del cobre es
10 N
1110 m 2 y su densidad de 8.8 cmg 3 .
Datos :
v
  8.8 cmg  8.8  10 3 mKg
Y  11 10 10 mN2
3
3
Y


11 10 10 mN2
8.8  10 3 mKg3
v  3 535.53 ms
2.
La velocidad del sonido en el aire es de 331 ms a 0 º C , calcular la velocidad del
sonido a 24 º C .
Datos :
v1  331 ms
v2
v1
T1  0 º C  273 º K

T2
 v 2  v1
T1
T 2  24 º C  297 º K
T2
T1
 331 ms
297 º K
273 º K
v 2  345 ms
Ejercicios.
1.
La densidad del agua es 10 3
Kg
m3
y la velocidad del sonido en el agua de 1 450 ms .
Calcular el módulo de compresibilidad del agua.
2.
A 0 º C la velocidad del sonido es de 331 ms , ¿a qué temperatura la velocidad
aumenta en un 5 % ?

Efecto Doppler
Naturaleza del efecto Doppler. El efecto Doppler es la variación de tono que
sufre un sonido cuando existe movimiento relativo entre una fuente de s onido y un
observador, como el tono depende de la frecuencia, es claro que la variación de tono
es debido a una variación de la frecuencia, pero la frecuencia de la fuente es
constante, por lo tanto la variación de frecuencia tiene que deberse al movimient o
relativo entre la fuente y el observador.
128
Clasificación del movimiento relativo en el efecto Doppler. El movimiento
relativo entre la fuente sonora y el observador puede ser de tres tipos.
1.
La fuente sonora está en movimiento y el observador en reposo.
2.
La fuente sonora está en reposo y el observador en movimiento.
3.
Tanto la fuente sonora como el observador están en movimiento.
Ecuaciones del efecto Doppler. Nuestro objetivo es deducir las ecuaciones
para calcular la frecuencia aparente que percibe el observador en los seis casos, que
son.
1.
La fuente está en reposo y el observador se acerca.
2.
La fuente está en reposo y el observador se aleja.
3.
La fuente se acerca a un observador en reposo.
4.
La fuente se aleja de un observador en reposo.
5.
El observador y la fuente se mueven acercándose.
6.
El observador y la fuente se mueven alejándose.
Primer caso: La fuente está en reposo y el observador se acerca.
vo
vs  0
Fig. 1
En la Fig . 1 un observador se acerca con velocidad “ v o ” a una fuente sonora en
reposo. Si el observador estuviera en reposo, el sonido tardaría un tiempo “ t ” en
llegar a él al recorrer la distancia “ d ” que separa a la fuente del observador. Esta
distancias “ d ” es igual al número de ondas “ n ” por la longitud de onda “  ”. Como.
v
d
, d  vt  n
t
El número de ondas que llegaría al observador en el tiempo “ t ” sería.
n
vt

129
Sin embargo, debido a su movimiento hacia la fuente, el observador percibe un
número “ n ' ” de ondas adicionales, siendo.
n'
vo t

Entonces el número total de ondas que percibe el observador en el intervalo “ t ”
es.
n  n'
vt

vo t



t v  v o


La frecuencia es el número de ondas en la unidad de tiempo, pero la frecuenci a
que percibe el observador es una frecuencia aparente, que es.
f '
Como v   f , entonces  
n  n'

t
t v  v o

t


v  vo

v
, por lo tanto la frecuencia aparente es.
f
f '
v  vo
v
f
Reacomodando y factorizando, tenemos.
 vo 
f '  f 1  
v

1
Que es la primera ecuación buscada.
Segundo caso: La fuente está en reposo y el observador se aleja.
vo
vs  0
Fig. 2
130
Si estuviera en reposo, el número de ondas que llegarían al observador en un
vt
tiempo “ t ” sería n  , pero debido a su movimiento alejándose de la fuente, el

vo t
observador deja de percibir un número “ n ' ” de ondas, siendo n ' 
, entonces el

número total de ondas que percibe el observador en el intervalo de tiempo “ t ” es.
n  n'
t v  v o


La frecuencia aparente que percibe el observador es el número de ondas en la
unidad de tiempo.
n  n' t v  vo
f '

t
t

Como v   f , entonces  

v
, por lo tanto la frecuencia aparente es.
f
v vo
f '
v
f
Reacomodando y factorizando, tenemos.
 vo 
f '  f 1  
v

2
Que es la segunda ecuación buscada.
Tercer caso: La fuente se acerca a un observador en reposo.
vs
Fig. 3
131
vo  0
El efecto que experimentan las ondas sonoras cuando la fuente se mueve hacia
v
el observador en reposo es un acortamiento en un factor s , que es la distancia que
f
avanza la fuente en dirección al obser vador. Entonces la longitud de onda del sonido
que escucha el observador es.
 '
v vs vvs


f
f
f
Por lo tanto, la frecuencia aumenta, siendo.
f '
v
'

v
vvs
f
Reacomodando.
 v 
f ' f 

 v  v s 
3
Que es la tercera ecuación buscada.
Cuarto caso: La fuente se aleja del observador en reposo.
vs
vo  0
Fig. 4
El efecto que experimentan las ondas sonoras cuando la fuente se mueve
vs
alejándose del observador en reposo es un alargamient o en un factor
, por lo tanto,
f
la longitud de onda del sonido que escucha el observador es.
 '
v vo v  vs


f
f
f
132
Como f ' 
v
'
y  '   , entonces f '  f . La frecuencia reducida es.
f '
v
'
v
vvs

f
Reacomodando.
 v 
f ' f 

 v  v s 
4
Que es la cuarta ecuación buscada.
Quinto caso: La fuente y el observador se mueven acercándose.
vs
vo
Fig. 5
La frecuencia aparente que percibe el observador al acercarse a la fuente es.
f '
v  vo
'
En la que  ' es la longitud de onda reducida por el movimiento de la fuente
hacia el observador, siendo.
 '
vvs
f
Por lo tanto.
f '
v  vo
vvs
f
133
Reacomodando, tenemos.
v  vo 
f ' f 

 v  v s 
5
Que es la quinta ecuación buscada.
Sexto caso: La fuente y el observador se mueven alejándose.
vs
vo
Fig. 6
La frecuencia aparente que percibe el observador al alejarse de la fuente es.
f '
v vo
'
En la que  ' es la longitud de onda alargada por el movimiento de la fuent e
alejándose del observador, siendo.
 '
vvs
f
Por lo tanto.
f '
v vo
vvs
f
Reacomodando, tenemos.
v  vo 
f ' f 

 v  v s 
Que es la sexta ecuación busca da.
134
6
De las seis ecuaciones anteriores, tenemos que:
f ': Es la frecuencia aparente percibida por el observador.
f : Es la frecuencia real.
v : Es la velocidad del sonido.
v o : Es la velocidad del observador.
v s : Es la velocidad de la fuente.
Ejemplos.
1.
El silbato de una fabrica emite ondas sonoras con una frecuencia de 4 000 Hz . Si
un obrero se dirige hacia la fabrica con una velocidad de 20 ms , ¿cuál es la frecuencia
aparente del sonido que percibe?
f  4 000 Hz
vo  20 ms
Datos :
f  4 000 Hz
v o  20 ms
v  345 ms a 24 º C 

 vo 
20 
f '  f 1    4 000 1 

v

 345 
m
s
m
s
135
f ' 4 232 Hz
2.
El silbato de una locomotora que se mueve a 90 Km
tiene una frecuencia de
h
2 000 Hz . Calcular la frecuencia aparente del sonido que percibe una persona después
de haber pasado la locomotora. La velocidad del sonido en el aire es de 340 ms .
f  2 000 Hz
Datos :
f  2 000 Hz
m
v s  90 Km
h  25 s
v  340 ms
 v 
 340 ms

f ' f 

2
000


m
m
 v  v s 
 340 s  25 s 
f ' 1 863 Hz
Ejercicios.
1.
Calcular la velocidad a la que se aleja una persona de una alarma sabiendo que
la frecuencia que percibe es 10 % inferior a la realmente emitida.
2.
En un tramo recto de carretera, una ambulancia con una sirena emitiendo su
sonido a una frecuencia de 2 000 Hz avanza con una velocidad de 40 ms . En sentido
contrario avanza un automóvil con una velocidad de 20 ms , ¿con qué frecuencia
aparente llega el sonido de la sirena al automóvil?
136
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No.4
Reconocer que la luz es una onda electrom agnética, las teorías de su naturaleza, el
espectro electrom agnético; y las evidencias de que la luz en m edios uniform es se m ueve en
línea recta así com o el valor de su velocidad con cifras significativas .
La luz y sus características

Generalidades
Concepto de óptica. La óptica es la parte de la física que estudia la luz, los
fenómenos ópticos, sus leyes y sus aplicaciones.
Importancia de la óptica. La luz y sus distintos fenómenos presentan algunos
de los más interesantes estudios de la física, son interesantes porque los resultados de
muchos experimentos se manifiestan por medio del se ntido de la vista como
fenómenos de colores. Igualmente importante y de interés es la gran cantidad de
aparatos ópticos que nos rodean, tales como la cámara, el telescopio, el microscópio,
etc.
Óptica física y óptica geométrica. Todas las propiedades de la luz se pueden
describir en relación a los experimentos por medio de los cuales fueron descubiertos
y por los variados experimentos a través de los cuales son ahora demostrados. Al
agrupar estos experimentos podemos clasificar a la óptica en tres categorías.
1.
La óptica geométrica. Trata de los fenómenos ópticos que se
describen más fácilmente con el trazado de líneas rectas y de
geometría plana, como es el caso de la propagación rectilínea de la luz,
de su velocidad finita, así co mo de los fenómenos de reflexión y de
refracción.
2.
La óptica física. Se ocupa de la naturaleza ondulatoria de la luz;
difracción, interferencia, polarización y doble refracción.
3.
La óptica cuántica. Se refiere a los aspectos cuánticos de la luz, el
estudio de temas tales como el efecto fotoeléctrico, el efecto Compton
y la excitación atómica.
137
Concepto y naturaleza de la luz. Se llama luz al agente que ilumina los
objetos y los hace visibles. En la actualidad se acepta para la luz una doble
naturaleza:
4.
Corpuscular. Considera que la luz está constituída por partículas
llamadas fotones, los cuales son emitidos por los cuerpos luminosos.
5.
Ondulatoria. Este modelo considera a la luz como
electromagnética que es emitida por el cuerpo luminoso.
una
onda
Ambos modelos son aceptados porque algunos fenómenos que no se resuelven
con el modelo corpuscular se resuelven con el modelo ondulatorio y viceversa.
Espectro electromagnético. Dicho espectro es la representación por medio de
franjas de las ondas electromagnéticas. Di chas ondas están constituídas por un campo
eléctrico y otro magnético que oscilan en planos perpendiculares entre sí. Estas ondas
pueden ser producidas de diferentes formas: las originan los motores de corriente
alterna, los aparatos electrónicos, los apar atos de rayos X, las bombas nucleares y el
mismo Sol, entre otras.
Para representar el espectro electromagnético primeramente se definen las
bandas y sus subdivisiones de que están compuestas, después se epecifica la longitud
de onda, la frecuencia y energ ía de esas bandas. Posteriormente se colocan los
nombre de lo diferentes tipos de ondas electromagnéticas, y debajo de ellas, a manera
de escala, los valores correspondientes de longitud de onda, frecuencia y energía.
Muchas veces las bandas no están bien definidas, sino que se traslapan unas con
otras. El espectro electromagnético está representado en la siguiente figura.
138
R
i
a
d
o
n
i
i
a
z
c
a
i
n
ó
t
n
e
Rayos R
gamma a
y
o
s
3  10
15
3  10
3  1013
X
Ultra
violeta
visible
n
a
d
i
a
c
i
ó
n
Infra
o
Calor
rojo
i
o
n
i
z
a
R
n
a
t
d
e
i
o
f
r
e
c
u
e
n
c
i
a
s
10
14
Luz
R
10
Micro
ondas
EHF
VLF
10  6
10 5
10  4
10 3
10  2
10 1
c
u
e
n
c
i
3  10 4
3  10 3
3  10 2
1
10
10 2
a
3  10
3  10 0
10
10 4
3  10 1
3  10  2
10 5
10 6
HF
LF
r
e
3  10
3  10 9
3  108
3  10 7
3  10 6
3  10 5
VHF
10 8
10  7
F
10
UHF
MF
10
10 9
3  1012
3  1011
SHF
11
3

10 6
L
10 5
10 4
10 3
o
n
g
10 2
10
1
10 1
10  2
10 3
i
t
u
d
d
e
10  4
10 5
10  6
10  7
10 8
o
n
d
a
E
n
e
r
g
í
a
10 9
10 10
10 11
10 12

Donde la frecuencia está medida en megahertz 1 MHz  106 Hz , la longitud de
onda en centímetros y la energía en electron -volts 1 ev  1.6 10 19 J .

EHF : Extemadamente alta frecuencia.
SHF : Super alta frecuencia.
UHF : Ultra alta frecuencia.
VHF : Muy alta frecuencia.
HF :
Alta frecuencia.
MF :
Media frecuencia.
LF :
Baja frecuencia.
VLF : Muy baja frecuencia.
139

Las ecuaciones que relacionan a la frecuencia, la longitud de onda y la energía
de las diferentes bandas del espectro electromagnético son.
c f
Donde:
c : Es la velocidad de la luz en el aire o vacío 3108
m
s

f : Es la frecuencia de las radiaciones en hertz.
 : Es la longitud de la onda (radiación) en metros.
Eh f
Donde:
E : Es la energía de la radiación electromagnética en Joules.
h:
Es
una
constante
de
proporcionalida
llamada
cosntante
de
Plank,
h  6.625 10 34 HzJ
Un electrón volt ev  es la energía que contiene un electrón a la diferencia de
potencia de un volt. Para calcularla se usa la relación.
1 ev  1.6 10 19 J
Para expresar las unidades de longitud de onda se utilizan los siguientes
submúltiplos.
micra :   106 m
milimicra : m   109 m
  1010 m
ángstron : 
Principio de Huygens. Huygens consideró a la luz totalmente ondulatoria y su
principio explica la propagación de las ondas luminosas y permite localizar los
futuros frentes de onda que ocuparán éstas en su propagación.
a)
Una fuente luminosa produce un frente de ondas en forma de ondas
esféricas concentricas cuyo centro es el foco luminoso o fuentes
luminosas.
b)
Cada punto de estas ondas constituye una perturbación que da lugar a
la generación de una nueva fuente de ondas esf éricas, y así
suscesivamente.
c)
A cada nuevo frente de ondas aparecerá una nueva esfera de radio “ r ”
v
y cuya longitud es igual a la longitud de la onda, siendo r  , donde
f
“ v ” es la velocidad de la l uz y “ f ” es la frecuencia.
140
Tomando cada uno de los cualesquiera puntos “ a ”, “ b ” y “ c ” como fuentes
puntuales iguales a “ S ” ondas secundarias, se esparcirán y un instante después su
envolvente es un nuevo frente de ondas “ A ”, “ B ” y “ C ”, y repitiendo el proceso,
posteriormente se formará un frente de onda “ L ”, “ M ” y “ N ”
L
A
a 
r
v
f
B
a
M
b
s
c
C
N
Fuente
Fig . 1
luminosa
Concepto de rayo. Un rayo es un segmento de recta dirigio e imaginario. En el
modelo corpuscular, un rayo es la trayectoria seguida por un fotón; en el medio
ondulatorio, indica la dirección de propagación de la onda luminosa.
Cuerpos luminosos e iluminados. Los cuerpos luminosos son los que emiten
luz propia, tales como el Sol, las estrellas, el filamento incandescente de una
lámpara, la llama de un mechero de gas o un cerillo encendido. Existen cuerpos
luminosos en cualquiera de los tres est ados físicos. Los cuerpos iluminados son los
que no poseen luz propia y, por lo tanto, no se ven en la oscuridad, sin embargo, los
cuerpos iluminados se hacen visibles al reflejar la luz que reciben de un cuerpo
luminoso.
141
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No.5
Definir los térm inos intensidad lum inosa, f lujo lum inoso e iluminación.
Cuerpos opacos, transparentes y translúcidos. Si se intercalan entre un
observador y un foco luminoso distintos cuerpos, se observa:
1.
Algunos cuerpos al interpone rse entre el foco luminoso y el observador
impiden a éste ver el foco luminoso. Estos cuerpos se llaman opacos e
impiden el paso de la luz a través de ellos.
2.
El aire, una lámpara de vidrio, el agua, etc., permiten al observador
ver el foco luminoso. Estos cuerpos reciben el nombre de transparentes
o diáfanos y permiten el paso de la luz con facilidad.
3.
Otros cuerpos dejan pasar la luz, pero no permiten ver con precisión
los objetos colocados detrás de ellos. Estos cuerpos se llaman
translúcidos. Ejemplos: el cristal esmerilado, una placa de acrílico o
una hoja de papel impregnada de aceite.
Sombra y penumbra. Para que exista sombra, se deben cumplir las siguientes
condiciones.
a)
Se debe contar con un manantial luminoso.
b)
Se debe disponer de un cuerpo luminoso.
c)
Se debe disponer de una pantalla para formar la sombra.
Entre la pantalla y el manantial luminoso se coloca el cuerpo opaco, los rayos
que emanan del manantial chocan contra la pantalla con excepción de aquellos rayos
que fueron reflejados por el cuerpo opaco. La zona de la pantalla donde no hay luz es
lo que constituye la sombra del cuerpo opaco.
142
Manantial
Cuerpo
luminoso puntual
opaco
Fig . 2
Pantalla
Sombra
Para que exista penumbra, debe de haber una fuente luminosa, pero no puntual,
además de también se presenta la sombra. La penumbra se presenta debido a los rayos
tangenciales sobre el cuerpo opaco, internos y externos.
Pantalla
Manantial
luminoso no puntual
Cuerpo opaco
Sombra
Fig . 3

Penumbra
Velocidad de la luz
Experimento de Galileo. La velocidad de la luz, dada la
gran importancia que tiene para la Física, es una de las constantes
que se ha medido con más precisión. Su valor es tan grande que
hasta antes de 1 675 no pudo determinarse experimentalment e;
antes de esto era creencia general que dicha velocidad era infinita,
ya que nada en nuestra experiencia cotidiana nos induce a pensar
lo contrario.
El experimento propuesto por Galileo en 1 667 constituye uno de los primeros
intentos por medir la velocidad de la luz. En este experimento realizado de noche, dos
personas se colocan a una cierta distancia portando una linterna cubierta que podían
destapar a voluntad. El primer observador descubría su linterna y al ver la luz, el
segundo observador descubria la suya.
143
Como se conocía la distanicia entre las dos linternas, Galileo pensaba que si se
medía el tiempo transcurrido entre el instante en que el primer observaador descubre
su linterna y el instante en que veía la luz de la otra linterna, podría calcular la
velocidad de la luz.
Actualmente sabemos que la velocidad de la luz es tan grande que aunque el
experimento de Galileo era en principio correcto, no pudo determinar su velocidad,
ya que el tiempo requerido por la luz para recorrer la distancia que separaba a los dos
observadores era tan pequeño que no pudo ser medido por Galileo. Ante la
imposibilidad de medir la velocidad de la luz, Galileo apuntó: Si no es instántanea,
es extraordinariamente rápida .
Experimento de Olaf Roemer .
Cinco años después, en 1 675 , el astrónomo danés Olaf Roemer, en virtud de
observaciones astrónomicas realizadas sobre uno de los satélites de Júpiter, obtuvo la
primera prueba terminante de que la luz se propaga con velocidad finita. Júpiter tiene
once lunas, cuatro de las cuales son suficientemente bri llantes para que puedan verse
con un telescopio. Los satélites aparecen como pequeños puntos brillantes a los lados
del disco del planeta. Estos satélites giran alrededor de Júpiter como la Luna lo hace
alrededor de la Tierra, y como el plano de sus órbita s es casi el mismo que aquel en
que giran la Tierra y Júpiter, cada uno de ellos es eclipsado por el planeta durante
una parte de cada revolución.
Roemer trataba de medir el patrón de uno de los satélites utilizando el intervalo
de tiempo transcurrido entr e dos eclipses consecutivos (unas 42 horas,
aproximadamente). Comparando los resultados obtenidos durante un largo tiempo,
encontró que cuando la Tierra se alejaba de Júpiter, los intervalos de tiempo eran más
largos que el valor medio, mientras que cuando se aproxima Júpiter a la Tierra, los
intervalos eran algo más cortos; de ello dedujo correctamente que la causa de estas
diferencias eran la variación de la distancia entre Júpiter y la Tierra.
La Fig . 4 (no dibujada a escala) aclara el caso: Suponiendo que l as
observaciones comienzan cuando la Tierra y Júpiter ocupan las posiciones T 1 y J 1 ,
puesto que Júpiter necesita doce años para recorrer su órbita, resulta que durante el
tiempo que ha tardado la Tierra en llegar a T 2 (unos cinco meses), Júpiter sólo se ha
movido a J 2 , y durante este tiempo la diferencia entre
aumentando continuamente, por consiguiente, en cada eclipse
satélite ha de recorrer una distancia ligeramente mayor que en
y el periodo de cada revolución observada es algo mayor que el
144
los planetas ha ido
la luz procedente del
el eclipse precedente,
verdadero.
Roemer dedujo de sus observaciones que la luz necesitaba un tiempo de unos 22
minutos para recorrer una distancia igual al diámetro de la órbita terrestre. El mayor
valor obtenido para esta distanc ia en tiempos de Roemer era aproximadamente
172 000 000 millas. No existe evidencia de que Roemer realizara el calculo, de haberlo
realizado con los datos anteriores, habría calculado una velocidad de 2.1108 ms .
Orbita de
Júpiter
Orbita de
Satélite
la Tierra
Sol
J1
T1
T2
J2
Fig . 4
Experimento de Fizeau. El primer método terrestre para medir la velocidad de
la luz fue realizado por el físico francés Fizeau en 1 849 . Su dispositivo experimental
se muestra en la Fig . 5 . El haz de luz de una fuente luminosa intensa “ S ” incide sobre
un espejo semitransparente “ E 1 ” y se refleja hacia la lente “ L 1 ”, la cual hace
converger el haz en el foco “ S ” localizado cerca del borde de la rueda dentada.
Consideremos que en un principio la rueda está qui eta y que la luz pasa a través
de una de las aberturas entre los dientes. Esta luz incide sobre la lente “ L 2 ”, la cual
convierte el haz de luz en rayos paralelos que viajan una distancia de 8 633 metros
hasta la cima de una colina donde inciden sobre una tercera lente “ L 3 ” que los hace
converger nuevamente formando la imagen en el espejo “ E 2 ”, la luz es reflejada
nuevamente en “ L 3 ”, y en forma de rayos paralelos, viaja de nuevo por la misma
trayectoria hasta “ L 2 ”, que la hace converger en “ F ”, posteriormente incide en “ L 1 ”
y al llegar al espejo semitransparente “ E 1 ” , una parte del haz es reflejada y la otra
parte llega hasta el observador.
Al girar la rueda dentada corta el haz de luz en destellos momen táneos con el
objeto de medir el tiempo empleado por esas señales en su viaje de ida y vuelta hasta
el espejo distante.
Si la velocidad angular de la rueda “  o ” es tal que el tiempo empleado por un
destello en llegar hasta el espejo y volver ésta, se ha mov ido de un hueco a un diente,
la luz será detenida por éste y no llegará al observador. Si se aumenta paulatinamente
145
la velocidad angular, la luz aparecerá de nuevo aumentando hasta brillar con máxima
intensidad, y esto ocurre cuando la velocidad angular es “ 2 o ” (o n o para “ n ” par).
Conociendo la velocidad angular, el radio de la rueda y la distancia entre las
aberturas, podrá calcularse el tiempo empleado por la rueda para pasar de un hueco a
otro. Este tiempo es igual al empleado por la luz en un viaje de i da y vuelta hasta el
espejo distante.
Usando una rueda que contenía 720 dientes, Fizeau observó la máxima
brillantez a la velocidad de 25 revoluciones por segundo, conocido el tiempo y la
distancia recorrida por la luz, calculó una velocidad de 313 000 Km
y dicha técnica es
s
conocida como el método de la rueda dentada.
E2
E1
L3
Fig . 5
L2
L1
S
Experimento de A. A. Michaelson. En años posteriores a los experimentos de
Fizeau, otros investigadores mejoraron su dispositivo experimental y determinaron
valores más precisos de la velocidad de la luz. En 1 862 el físico francés Foucault
realizó sus experimentos sustituyendo la rueda dentada por un espejo girarorio,
obteniendo un valor de 298 000 Km
s . Esta técnica es conocida como el método del
espejo giratorio.
Durante 50 años el físico estadounidense Albert A. Michaelson realizó un gran
número de experimentos utilizando el método del espejo giratorio y en 1 880
determinó el valor de la velocidad de la luz en 299 910 Km
con una incertidumbre de
s
Km
Km
50 s , y para 1 926 determinó un valor de 299 796 s con una incertidumbre de 4 Km
s .
Michaelson condideró que era posible obtener un valor más preciso midiendo la
velocidad de la luz en el vacío, y con la colaboración de Pease y Pearson construyó
un tubo de vacío de 1.6 Km de largo 1 milla  . Michaelson murió en 1 931 , pero sus
146
experimentos fueron comple tados por Pease y Pearson en 1 932 . Su dispositivo
experimetal se muestra en la Fig . 6 .
Un haz procedente de una lámpara de arco incide en el punto “ a ” sobre una de
las 32 caras de un espejo giratorio “ G ” y penetra en el tubo de vacío a través de la
ventana “ V ”. Después de reflejarse en el espejo plano “ E 1 ” incide sobre el espejo
cóncavo “ E 2 ” y después en el espejo plano “ E 3 ” para finalmente reflejarse
sucesivamete en los espejos “ E 3 ” y “ E 4 ” y después de la última travesía regresa al
espejo cóncavo “ E 2 ” donde se refleja de nuevo en “ E 1 ” para salir del tubo por la
ventana “ V ” e incidir sobre el espejo giratorio.
Si el espejo está en reposo la luz se refleja de manera conveniente en “ b ” para
que pueda ser vista por el observador, pero cuando el espejo está girando, la luz que
sale de la ventana se refleja en otra dirección y no puede ser vista. Se aumenta
entonces la velocidad de giro hasta que el espejo alcanza la posición correcta justo a
tiempo para que el haz de luz que sale por la ventana incida de nuevo en “ b ” para
reflejarse hacia el observador.
La velocidad con que gira el espejo se determina con exactitud por medio de
una comparación estroboscópica con una señal de frecuencia conocida emitida por un
diapasón. Esta velocidad resultó ser de 582 revoluciones por segund o.
El espejo giratorio tarda un tiempo “ t ” en pasar de la posición “ a ” a l a
posición “ b ”, mismo tiempo empleado por la luz en recorrer los 16 Km en el tubo de
vacío y salir. Hasta 1 932 Pease y Pearson llevaron a cabo 2 885 experimentos y el
valor promedio que encontr aron para la velocidad de la luz fue de 299 774 Km
con una
s
incertidumbre de 11 Km
s . El vacío que puede hacerse en el interior del tubo da una
presión de hasta 1 mm Hg (aproximadamente 0.001 atm o 133.3 Pa ), por lo que basta una
pequeña corrección para determinar la velocidad de la luz en el vacío.
Tubo de vacío
E2
E1
E4
E3
1.6 Km
V
G
Fig. 6
147
S
a
b
Desde los tiempos de Galileo
número de experimentos para medir
colaboradores de los Estado Unidos
técnicas de rayo láser y determinaron
tan sólo 0.0012 Km
s .
hasta nuestros días, se han realizado un gran
la velocidad de la luz. En 1 973 1, Evenson y
relizaron una serie de experimento s utilizando
un valor de 299 792 Km
con una incertidumbre de
s
Fórmula de Maxwell. Maxwell predijo mediante un desarrollo sistemático l a
velocidad de propagación de las ondas electromagnéticas luz  en el vacío, siendo:
c
1
o  o
1
Donde:
c:
Es la velocidad de la luz en el vacío.
:
Es la permitividad en el vacío.
 o : Es la permeabilidad en el vacío  o  4 10 7
H
m
.
Al aplicar la ecuación 1 , se obtiene para la luz una velocidad de 2.9986 108
A través de cualquier medio, la velocidad de las ondas electrom agnéticas es.
c
m
s
.
1
1


o r  o  r
Como  r y  r son mayores que la unidad, se comprende que la velocidad de la
luz en cualquier medio es menor que en el vacío.

Reflexión, refracción y dispersión de la luz
Reflexión. Es el cambio de dirección que experimentan las ondas luminosas
cuando al propagarse a través de un medio, inciden sobre una superficie llamada
reflectante. Al reflejarse la luz, continua propagándose por el mismo medio y, en
consecuencia, con la misma vel ocidad, aunque en otra dirección.
Leyes de reflexión. Se llama ángulo de incidencia al formado por un rayo
incidente y normal a la superficie en el punto de incidencia. El ángulo de reflexión es
el que forman el rayo reflejado y la normal. Las leyes de la reflexión son dos:
148
1.
El rayo incidente, el rayo reflejado y la normal a la superficie están
en un mismo plano.
2.
El ángulo de incidencia y el ángulo de reflexión, con respecto a la
normal, son iguales.
Normal
Rayo
Rayo
incidente
reflejante
Ángulo de
'

Ángulo de
reflexión
incidencia
Superficie reflejante
Fig . 1
Concepto de refracción. La refracción es el cambio de dirección que
experimenta la luz cuando al propagarse a través de un medio, incide sobre una
superficie llamada refractante, continuando su propagación en el mismo medio o en
otro medio. Cuando la luz incide sobre una superficie lisa de una sustancia
transparente, como agua o vidrio, parte de ella se refleja de acuerdo con la ley de
reflexión, y el resto se refracta, entrando al nuevo medio.
Rayo
Rayo
incidente
reflejado
Normal

'
Aire
Vidrio

Fig . 2
Rayo
refractado
Reflexión y refracción
149
Leyes de la refracción. Las leyes de la refracción son
dos:
1.
El rayo incidente, el rayo refractado y la normal a la
superficie refractante están en el mismo plano.
2.
La razón del seno del ángulo de incidencia al seno
del ángulo de refracción es igual a la razón de las
velocidades de propagación de la luz en cada uno de
los medios considerados, o sea.
sen  v

sen  v '
Donde:
 : Es el ángulo de incidencia con respecto a la normal.
 : Es el ángulo refractado con respect o a la normal.
v : Es la velocidad de la luz en el medio donde incide el rayo.
v ': Es la velocidad de la luz en el medio donde el rayo se refracta.
Rayo
incidente
Normal

Medio A
Medio B

Fig . 3
Rayo
refractado
Refracción de la luz
Índice de refracción. Se define al índice de refracción como.
n
1
c
v
Donde:
c : Es la velocidad de la luz en el vacío.
v : Es la velocidad de la luz en un medio.
n': Es el índice de refracción en dicho medio.
150
Por la forma en que se define el índice de refracción, no tiene unidades. Como
la velocidad de la luz en el aire es prácticamente la misma que en el vacío, resulta
que el índice de refracción es prácticamente igual a uno.
La velocidad de la luz en cualquier medio más denso que el aire es menor que
“ c ”, y por lo tanto, mayor que 1. Al pe netrar la luz en cualquier medio más denso que
el aire, disminuye su velocidad porque disminuye su longitud de onda, pero la
frecuencia es la misma en cualquier medio.
Ley de Snell. Esta ley postula que la razón del seno del ángulo de incidencia al
seno del ángulo de refracción es igual a una constante, en términos matemáticos.
sen 
 cte
sen 
Como.
Entonces: n 
sen  v

sen  v '
c
c
v n'
sen  n '
y n '  , por lo tanto
 , así que
 , y racomodando
v
v'
v' n
sen  n
términos, tenemos.
n sen   n ' sen 
2
Que es la expresión matemática de la Ley de Snell y donde:
 : Es el ángulo de incidencia.
 : Es el ángulo de refracción.
n : Es el índice de refracción del medio donde incide el rayo.
n': Es el índice de refracción en dicho medio.
Refracción en un prisma. Después de las lentes el prisma, en cualquiera de sus
formas, es la pieza más útil de los instrumentos ópticos.
151
A
D
N
2
N
1
2
1
Fig . 4
Sea “ n ” el índice de refracción del prisma, “ A ” el ángulo en la arista, y para
facilitar los cálculos, podemos suponer que el medio situado a ambos lados del
prisma es aire. Un rayo de luz al ser refractado por el prisma es desviado un ángulo
“ D ” con respecto a su trayectoria original.
Con respecto a la no rmal de cada superficie, si el ángulo con que incide el rayo
al entrar al prisma es “  1 ” y el ángulo con que refracta al salir de éste es “  2 ”, se
puede demostrar mediante un análisis geométrico que el ángulo de desviación “ D ” se
puede expresar como.
D   1  2  A
El valor del ángulo “ D ” varía en función de “  1 ”, pero existe un valor de “  1 ”
para el cual el ángulo de desviación es mínimo y se expresa como “ D m ”. En este
caso, la trayectoria del rayo al entrar es paralela a la base del prisma y el ángulo “  2 ”
con que refracta al salir es igual a “  1 ”, y por lo tanto.
1  2 
Y entonces D m  2  A , por lo tanto.

Dm  A
2
152
3
Podemos calcular, así, el valor del ángulo de incidencia para el cual ocurre la
mínima desviación. Ahora necesitamos una expresión para calcular “ D m ”, según la
Fig . 5 , el ángulo con que se refracta el rayo al entrar al prisma es  1  12 A (lados
perpendiculares entre sí), además   12 D m porque en cada superficie se produce la
mitad de la desviación, en consecuencia    1    12 A  12 D m , sumando fracciones,
tenemos  
A  Dm
2
, y mediante la Ley de Snell sen   n sen  1 , por lo tanto.
sen
Dm  A
2
4
 n sen 12 A
Que es la ecuación buscada y donde:
A:
Es el ángulo en el prisma.
n:
Es el índice de refracción del prisma.
D m : Es el ángulo de mínima desviación.
1
2
A
1
2
A
Dm
N


1
Fig . 5
Dispersión. La dispersión es un fenómeno que se produce cuando un haz de luz
policromática pasa a través de un prisma y consiste en la descomposición de la luz en
los diferentes colores que la integran. Los distintos col ores del espectro visible tienen
diferentes longitudes de onda y frecuencias, en el aire, todos los colores tienen la
misma velocidad, pero al entrar en el prisma cada color experimenta sus diferentes
modificaciones en su longitud de onda y, en consecuenci a, cada color se mueve con
diferente velocidad.
El índice de refracción de una sustancia es función de la longitud de onda, por
lo tanto, cada color del espectro visible se refracta de manera diferente, de tal forma
que cada color se desvía de manera difer ente.
153
D
rojo
amarillo
anaranjado
verde
azul
violeta
Fig . 6
Mientras mayor sea la longitud de onda, menor será la desviación. En la Fig . 6
puede observarse que el ángulo de desviación para el rojo es menor que todos los
demás, siendo el violeta el que tiene la máxima desviación y, por lo tanto, el que
tiene menor longitud de onda.
154
Ejemplos.
1.
Un rayo de luz penetra en una lámina de vidrio con un ángulo de incidencia de
60 º , siendo una parte del rayo reflejada y la otra refracta da. Se observa que los rayos
reflejados y refractados forman entre sí un ángulo de 90 º , ¿cuál es el índice de
refracción del vidrio?


Aire
90 º
Vidrio

    90 º  180 º
  30 º
  180 º  90 º  180 º60 º90 º
sen   n sen 
n
sen  sen 60 º

sen  sen 30 º
n  1.73
2.
Un rayo de luz incide con un ángulo de 45 º en un prisma que tiene un ángulo
de 50 º en el vértice y un índice de refracción de 1.5, calcular el ángulo de
desviación.
Datos :
A  50 º
n  1.5
1  arc sen
 1  45 º
sen  1
n
 arc sen
sen 45 º
1.5
1  28.13 º
sen  1  n sen 1
sen  2  n sen  2
 1  2  180  A  180 º
2  A   1  50 º 28.13 º
 2  arc sen n sen  2   arc sen 1.5 sen 21.87 º 
2  21.87 º
 2  33.96 º  34 º
D   1   2  A  45 º 34 º 50 º
D  29 º
155
3.
Un prisma tiene un ángulo de 58 º en el vértice y un índice de refracción de 1.6.
Calcular el ángulo de mínima desviación.
Datos :
A  58 º
sen
sen
n  1.6
A  Dm
A  Dm
2
2
A  Dm
 n sen 12 A
2
D m  250.86 º   A
 1.6 sen 12 58 º   0.775
A  Dm
2
 50.86 º
D m  43.74 º
 arc sen 0.775
Ejercicios.
1.
La velocidad de la luz en cierto medio es 1.6 108
de refracción en dicho medio?
m
s
, ¿cuál es el valor del índice
2.
Para un cierto material transparente el ángulo de refracción es de 25 º cuando el
ángulo de incidencia es de 40 º , ¿cuál es la velocidad de la luz en este medio?
3.
Un prisma tiene un ángulo de 55 º en el vértice y su índice de refracción es de
1.65. Calcular el ángulo con que un rayo debe incidir en el prisma para que el ángulo
de desviación sea mínimo.
156
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No.6
Identificar las im ágenes que se producen en un esp ejo plano, espejo esférico y en lentes.

Generalidades
Concepto de espejo, tipos de espejos y características de un
espejo es una superficie que ha sido pulida con el objeto de reflejar
espejos pueden ser planos y esféricos y éstos, a su vez, se clasifican en
convexos. En general, para abordar un problema de espejos necesitamos
siguientes caraterísticas.
espejo. Un
la luz. Los
cóncavos y
conocer las

Centro de curvatura. Es el centro de la esfera que determina la cara
del espejo y se representa con la letra “ C ”.

Radio de curvatura. Es la distancia del centro de curvatura a la cara
del espejo y se representa con la letra “ R ”.

Eje del espejo. Es la recta horizontal que une el centro de curvatura
con el centro del espejo.

Vértice. Es el punto que resulta de la intersección del eje del espejo
con la superficie del mismo.

Foco. El foco de un espejo es la imagen de un punto del eje que se
encuentra infinitamente alejado. El foco se representa con la letra
“ F ”.

Distancia focal. Es la distancia que hay del foco al vértice. Se
representa co la letra “ f ”.

Distancia objeto. Es la distancia que hay del objeto al vértice medida
sobre el eje del espejo y se representa con la letra “ o ”.

Distancia imagen. Es la distancia que hay del vértice al punto del ej e
donde se forma la imagen, representándose con la letra “ i ”.
Características de la imagen. Visto el espejo por el borde, la imagen se puede
formar a la izquierda o a la derecha. Al lado izquierdo del espejo se le denomina lado
real y al lado derecho se le denomina lado virtual; por tal motivo, sí la imagen se
forma del lado izquierdo se dice que la imagen es real, y sí se forma del lado derecho
se dice que la imagen es virtual . Dependiendo de la posición del objeto con respecto
al vértice y del tipo de espejo, la imagen puede a parecer derecha o invertida y puede
ser mayor, igual o menor que el objeto.
Convenciones.

La luz siempre se considerará propagándose de izquierda a derecha.

El objeto siempre estará a la izquierda del espejo.
157
Convención de signos.
1.
La distancia del objeto “ o ” siempre será positiva   .
2.
Cuando la imagen se forma a la izquierda del espejo (imagen real), la
distancia “ i ” será positiva   .
3.
Cuando la imagen se forma a la derecha del espejo (imagen virtual), la
distancia “ i ” será negativa   .
4.
El radio de curvatura “ R ” a la izquierda del espejo es positivo   .
5.
El radio de curvatura “ R ” a la dercha del espejo será negativo   .
6.
Sí el foco está a la izquierda del espejo, la distancia focal “ f ” es
positiva.
7.
Sí el foco está a la derecha del espejo, la distancia focal “ f ” es
negativa.
TABLA DE CONVENCIONES
IZQUIERDA
LADO REAL
DERECHA
LADO V IRTUAL
RAYO INCIDENTE
RAYO REFLEJADO
i  
i  
R  
R  
f  
f  
o  
o  
Ecuación de los espejos. Nuestro objetivo es deducir la ecuación de los
espejos en sus dos formas: en función del radio de curvatura y en función de la
distancia focal. Analicemos los triángulos de la Fig . 1 .
A
 
O



I
C
i
r
o
Fig . 1
158
V
Del triángulo OAC :           , de donde.
 A
   
Del triángulo OIA :   2        , de donde.
B
    2
Combinando las ecuaciones  A y B  para eliminar “  ”, obtenemos.
C 
    2
Los ángulos “  ”, “  ” y “  ” se pueden expresar así.

V
o

V
R

V
i
Entonces la ecuación C  se puede escribir.
 V  V 2  V 


o
i
R
Simplificando.
1 1 2
 
o i R
1
Que es la ecuación de los espejos en función del radio de curvatura y que es la
primera ecuación buscada.
Si suponemos i  f , por definición se cumple que o   , y por lo tanto
entonces la ecuación 1 se reduce a la forma.
1 2

f R
D 
f  12 R
2
Y despejando.
159
1
0,
o
Resultado importante porque nos permite ubicar el foco de un espejo en el
punto medio entre el vértice y el centro de curvatura. Sustituyendo la ecuación D  en
la ecuación 1 , obtenemos.
3
1 1 1
 
o i f
Que es la ecuación de los epejos en función de la distancia focal y que es la
segunda ecuación buscada y donde:
o : Es la distancia objeto.
i : Es la distancia imagen.
f : Es la distancia focal.
R : Es el radio de curvatura del espejo.
Aumento lateral. Se llama aumento lateral “ M ” a la relación que existe entre
las alturas del objeto y de la imagen. Nuestro objetivo es deducir las ecuaciones que
nos permitan calcular el aumento lateral y la altura de la imagen.
O'
h


I
O
h'
V
I'
i
Fig . 2
o
En la Fig . 2 el rayo que pasa por “ O ' ” incide en “ V ” con un ángulo “  ” y se
refleja con el mismo ángulo pasando por “ I ' ” y formando dos triángulos semejantes:
h h'
I V I ' y O'V O , por lo tanto  , de donde.
o i
i h'
E 

o h
h'
Al cociente
se le llama aumento lateral, por lo tanto.
h
h'
F 
M
h
160
Sustituyendo “ M ” de F  en E  , tenemos que.
M
G 
i
o
Con el objeto de que “ M ” sea negativo cuando la imagen esté invertida,
incorporamos un signo menos   y la ecuación G  se escribe.
M 
4
i
o
Que es la primera ecuación buscada y en la que “ M ” se expresa en función de
la distancia objeto y de la distancia imagen. Conocido el aumento lateral, podemos
h'
conocer la altura de la imagen recordando que M  , de donde.
h
5
h' M h
Que es la segunda ecuación buscada y en la cual “ h ” es la altura del objeto y
“ h ' ” es la altura de la imagen.
Construcción geométrica de imágenes. Conocida la posición del objeto con
respecto al vértice se puede construir su imagen geométricamente con el trazo de
cualesquiera dos de tres rayos notables que son.
1.
El que pasa por el centro de curvatura y se refleja sobre sí mismo .
2.
El que incide paralelamente al eje del espejo y se refleja pasando por
el foco.
3.
El que incide pasando por el foco y se refleja paralelo al eje del
espejo.
O
I
C
Fig . 3
161
F
Dependiendo del tipo de espejo y de la distancia objeto, los rayos notables al
reflejarse divergen y las imágenes virtuales (a la derecha del vértice) se construyen
por la convergencia de sus prolongaciones.
C
I F
V
O
Fig . 4

Espejo cóncavo
Concepto de espejo cóncavo.

Un espejo cóncavo es áquel que refleja la luz por la cara interna de un
casquete esférico.

Respetando la convención de que la luz incide por la izquierda, en los
espejos cóncavos, el centro de curvatura está a la izquierda del vértice
(y en consecuencia, el radio y el foco también están a la izquierda).
De acuerdo con la Fig . 1 , los rayos que llegan paralelos al eje de un espejo
cóncavo se reflejan y convergen en el foco.
Eje
F
C
Fig . 1
162
V
Convenciones.

El objeto estará a la izquierda del espejo y la distancia “ o ” siempre
será positiva   .

Como en los espejos cóncavos el foco está a la la izquierda del espejo,
la distancia focal “ f ” es positiva   .

El radio de curvatura “ R ”, por estar a la izquierda del espejo, es
positivo (obsérvese que “ R ” y “ f ” están a la izquierda.
Determinación analítica de la imagen.

Conocida la distancia objeto y la distancia focal (o el radio de
curvatura), se puede calcular la distancia imagen con la ecuación de
los espejos en cualquiera de sus formas.
1 1 1
 
o i f
1 1 2
 
o i R
Si el valor de “ i ” es negativo significa que la imagen es virtual (aparece a la
derecha del espej o).

Conocida la distancia imagen, se puede calcular el aumento lateral con
la ecuación.
N 

1
o
Conocido el aumento lateral, se puede calcular la altura de la imagen
con la ecuación.
h' M h
Recuérdese que si “ M ” es negativo y, en consecuencia “ h ' ” resulta negativa,
significa que la imagen está invertida.
Construcción geométrica de imágenes. Si recordamos que conocida la
posición del objeto con respecto al espejo, se puede construir la imagen
geométricamente con el trazo de dos de tres rayos notables que son.
1.
El que pasa por el centro de curvatura y se refleja sobre sí mismo.
2.
El que incide paralelamente al eje del espejo y se refleja pasando por
el foco.
3.
El que incide pasando por el foco y se refleja paralelo al eje del
espejo.
163
Las características de la imagen van a d epender de la distancia del objeto al
vértice. En las siguientes figuras se ilustran los cinco casos posibles y las
caraterísticas de la imagen.
1er caso :
OC
O
I
C
F
V
Imagen : Real
Invertida
h'  h
Fig . 2
2o caso :
OC
O
F
I C
V
Imagen : Real
Invertida
h'  h
Fig . 3
3er caso :
C OF
I
C O
F
V
Fig . 4
164
Imagen : Real
Invertida
h'  h
4o caso :
OF
C
O
V
No hay imagen
Se forma en
el infinito 
Fig . 5
F
C
O
Fig . 6
V
50 caso :
OF
Imagen : Virtual
Derecha
h'  h
I
Ejemplos.
1.
Un objeto de 3 cm de altura se coloca a 15 cm del vértice de un espejo cóncavo
que tiene un radio de curvatura de 12 cm .
a)
Determinar la posición de la imagen.
Datos :
h  3 cm
o  15 cm
i 1 1
 
o i f
R  12 cm
15 6
of
i

o f
15  6
i  10 cm
“ i ” es positiva, por lo tanto la imagen es real (está a la izquierda del espejo).
b)
¿Cuánto mide la imagen?
M 
i
10
2
 
o
15
3
 2
h '  M h     3 cm 
 3
h ' 2 cm
165
El signo menos significa que la imagen está invertida.
c)
Construir la imagen geométricamente.
F
I
C
O
V
2.
Al colocar un objeto a 20 cm del vértice de un espejo cóncavo cuya distancia
focal es de 40 cm , la imagen tien un aumento de 2. Al mover el objeto, el aumento de
la imagen tiene un valor de 4 .
a)
¿El objeto se acercó o se alejó de él?
Datos :
o 1  20 cm
f  40 cm
M2 
i2
4
o2
M1  2

M2  4
1
1

i2
4o 2
Sustituyendo el inverso de “ i 2 ” en la ecuación de los espejos 
1
4
1
y


4o 2 4o 2
f
despejando “ o 2 ”, tenemos que.
o2 
3 f 3 40 cm 

4
4
o 2  30 cm
El objeto se alejó del vértice.
b)
¿Qué distancia se desplazó el objeto con respecto a su posición inicial?
 o  o 2  o1  30 cm  20 cm
 o  10 cm
El objeto se alejó 10 cm del espejo.
166
Ejercicios.
1.
Frente a un espejo cóncavo de 8 cm de radio de curvatura se colocan dos
objetos, uno a 6 cm del vértice y el otro a 12 cm del vértice, ¿cuál es la distancia entre
las dos imágenes?
2.
Un objeto de 4 cm de altura se coloca en el punto medio de la distancia foca l de
un espejo cóncavo que tiene un radio de curvatura de 20 cm .
a)
Calcular el tamaño de la imagen.
b)
Calcular la distancia entre el objeto y su imagen.

Espejo convexo
Concepto de espejo convexo.

Un espejo convexo es áquel que refleja la luz por la cara externa de un
casquete esférico.

Respetando la convención de que la luz incide por la izquierda, en los
espejos convexos el centro de curvatura está a la derecha del vértice ( y
en consecuencia el radio y el foco también están a la derecha). De
acuerdo con la Fig . 1 , los rayos que llegan paralelos al eje de un espejo
convexo se reflejan y divergen como si procedieran de un foco.
F
V
C
Fig . 1

En los espejos convexos, la imagen siempre es virtual y derecha y
crece a medida que el objeto se acerca al vértice.
167
Convenciones.

El objeto estará a la izquierda del espejo y la distancia “ o ” siempre
será positiva   .

Como en los espejos convexos el foco está a la derecha del vértice, la
distancia focal “ f ” es negativa.

El radio de curvatura “ R ”, por estar a la derecha del vértice, es
negativo (obsérvese que “ R ” y “ f ” están a la derecha).
Determinación analítica de la imagen. Conocida la distancia objeto y la
distancia focal (o el radio de curvatura) se puede calcular la distancia imagen con la
ecuación de los espejos en cualquiera de sus dos formas.
1 1 1
 
o i f
1 1 2
 
o i R
Como en los espejos convexos la imagen siempre es virtual (aparece a l a
derecha del vértice), el valor de “ i ” siempre será negativo.

Conocida la distancia imagen se puede calcular el aumento lateral con
la ecuación.
M 

1
o
Conocido el aumento lateral se puede calcular la altura de la imagen
con la ecuación.
h' M h
Como en los espejos co nvexos la imagen aparece a la derecha, el valor de “ h ' ”
deberá ser positivo.
Construcción geométrica de imágenes. Conocida la posición del objeto con
respecto al espejo, se puede construir la imagen geométricamente con el trazo de dos
de tres rayos notables que son.
1.
El que incide sobre el espejo en la dirección del centro de curvatura y
se refleja sobre sí mismo.
2.
El que incide sobre el espejo en la dirección del foco y se reflej a
paralelo al eje.
3.
El que incide paralelamente al eje del espejo y se refleja com o si
procediera del foco.
168
C
F
V
Fig . 2
La imagen que se obtiene en un espejo convexo siempre es virtual, derecha y
más pequeña que el objeto; el tamaño de la imagen crece a medida que el objeto se
acerca al vértice.
O1
C
I 2 I1 F
V
Fig . 3
Ejemplos.
1.
Frente a un espejo convexo que tiene una distancia focal de 8 cm se coloca un
objeto. La imagen tiene un aumento de 52 , ¿qué distancia hay entre el objeto y su
imagen?
Datos :
f  8 cm
M
i 2

o 5
 i
M 
169
2
5
2o
5
Sustituyendo “ i ” en la ecuación de los espejos 
tenemos que.
o
Como i  
3f
3  8 cm 

2
2
2o
2 12 cm 

5
5
5
2
i
y despejando “ o ”,


2o 2o f
 o  12 cm
 i  4.8 cm
La imagen es virtual (está a la derecha del espejo), ahora calcularemos l a
distancia.
d  16.8 cm
d  o  i  12 cm  4.8 cm
2.
Al colocar un objeto frente a un espejo convexo que tiene una curvatura de
10 cm , la imagen que se forma mide 15 mm de alto y tiene un aumento de 12 .
Determinar gráfica y analíticamente las características del objeto y de su imagen.
R  10 cm  f  5 cm 
M 
Datos :
h '  15 mm
i
o
 i
1
2
o
2
Sustituyendo “ i ” en la ecuación de los espejos 
o   f   5 cm.
M
2 1 1
y despejando “ o ”;
 
o o f
 o  5 cm
Calculamos “ i ”.
I  2.5 cm
La imagen es vi rtual porque está a la derecha del espejo. Calculamos la altura
del objeto.
h' M h
 h
h  30 mm
El objeto tiene una altura de 30 mm .
170
h ' 15 mm

M
0.5
O
V
I
F
C
Ejercicios.
1.
Al colocar un objeto frente a un espejo convexo que tiene un radio de curvatura
de 16 cm , el aumento de la imagen es 12 . Calcular a qué distancia se debe colocar el
objeto del vértice si se desea un aumento de 14 .
2.
Al colocar un objeto de 30 mm de altura frente a un espejo convexo que tiene un
radio de curvatura de 10 cm , el aumento de la imagen es 12 , y al cambiar de posición
el objeto, el aumento de la imagen es de 53 .
a)
¿Qué tanto cambió de tamaño la imagen?
b)
¿Qué tanto se ace rcó o se alejó el objeto del vértice?

Espejo plano
Concepto de espejo plano. El espejo plano se puede conceptuar como una
porción muy pequeña de un espejo convexo cuyo centro de curvatura se encuentra en
el infinito, lo que significa que su radio de curvat ura se extiende hasta el infinito.
Respetando la convención de que la luz incide por la izquierda y que, por la analogía
con el espejo convexo, el radio de curvatura y el foco deberán estar a la derecha del
espejo y, sin embargo, para efecto de una determi nación analítica o geométrica de la
imagen es irrelevante considerar que “ R ” y “ f ” tengan valores negativos.
En los espejos planos la imagen siempre es virtual, derecha (aunque falseada) y
del mismo tamaño que del objeto, el cual siempre estará a la izquie rda del espejo y la
distancia objeto “ O ” siempre será positiva   . La distancia imagen “ i ” siempre será
negativa por ser la imagen virtual (aparece a la derecha del espejo).
171
Determinación analítica de la imagen.

Para conocer la distancia imagen, podemos usar la ecuación de los
espejos en cualquiera de sus dos formas, por ejemplo:
1 1 1
 
o i f
Pero como f   , entonces
1
 0 , por lo tanto, la ecuación anterior se reduce a
f
la siguiente expresión.
1 1
 0
o i
Despejando “ i ”, tenemos.
1
i  o

Para conocer el aumento lateral.
i
o
M  
1
o
o
El aumento siempre será igual a la unidad y la imagen siempre será derecha.

Para determinar la altura de la imagen.
h' M h
Pero como M  1, entonces.
2
h' h
La imagen siempre tendrá la misma altura que el objeto.
Construcción geométrica de imágenes.

Los rayos de luz que llegan perpendiculares al plano del espejo s e
reflejan sobre sí mismos.

Los rayos de luz que llegan formando un ángulo “  ” con la normal, se
reflejan formando el mismo ángulo “  ” (primera ley de la reflección).
La imagen se construye con la intersección de las p rolongaciones a l a
derecha del espejo.
172
De acuerdo con la Fig . 1 , la imagen de un objeto puntual situado en “ O ” es
virtual. Los rayos parecen salir de “ I ”, pero en realidad han sido reflejados por el
espejo.
Espejo


O
I


Fig . 1
o
i
La imagen siempre tendrá la misma altura que el objeto y una persona podrá ver
su imagen de cuerpo entero reflejada en un espejo plano que tenga solo la mitad de la
altura.
h
h'
O
Fig . 2
I
Una persona puede ver su imagen de cuerpo entero reflejada en un espejo plano
que solo tenga la mitad de su altura.
1
2
h
h
h
h'
O
Fig . 3
173
Ejemplos.
1.
Un muchacho de 1.60 m de estatura ve su imagen en un espejo plano vertical,
sus ojos se encuentran a 1.50 m del suelo, determinar la altura del espejo y a qué
altura se encuentra su base con respecto al suelo.
De acuerdo con la Fig . 3 , deducimos rápìdamente que el espejo debe tener una
altura de 80 cm y como los ojos del muchacho se encuentran a 1.50 m del suelo, la
base del espejo debe encontrarse a la mitad de esta altura, o sea, a 75 cm
2.
Un muchacho sostiene un letrero entre sus manos y ve su imagen reflejada en
un espejo plano vertical que se encuentra a 2 m de él. ¿Para qué distancia tiene que
afocar sus ojos para leer el letrero?
Datos :
o2m
Como i  -o, entonces i  -2 m
Calculo de la distancia.
d  o i  2 m 2 m
d 4m
Ejercicio.
1.
Un objeto se encuentra a 1 m de un espejo plano vertical y atrás del objeto se
encuentra una persona colocada a 3 m de distancia del espejo, ¿a qué distancia ve esta
persona la imagen del objeto?
174
Lentes

Generalidades
Concepto de lente. Una lente es un sistema óptico limitado por superficies
refringentes que tienen un eje común. En general, las superficies refringentes pueden
ser planas o porciones de esfera.
Tipos de lentes. Para su estudio, las lentes pueden clasificarse como.

Sencillas o compuestas.

Gruesas o delgadas.

Convergentes o divergentes.
Una lente sencilla es aquella que tiene únicamente dos superficies refringentes,
ejemplos son la lupa o los cristales de unos anteojos, mientras que las lentes
compuestas tienen más de dos sup erficies refringentes, como el objetivo de una
cámara fotográfica o el objetivo de un microscópio.
Una lente gruesa es aquella que al ser atravesada por un rayo de luz (que no sea
normal a la superficie de incidencia), éste experimenta una dobre refraci ón.
De acuerdo con la Fig . 1 , un rayo que atraviesa a una lente gruesa experiementa
una dobre refracción.
Una lente delgada es aquella en que la separación entre las dos superficies es
tan pequeña (en la dirección del eje de la lente) que se puede suponer que l a
refracción que experimenta un rayo de luz tiene lugar en el centro de la lente y, por
lo tanto, habrá una sola refracción, como se observa en la Fig . 2 .
175
Lente
Rayo
incidente
Eje de
la lente
Rayo
refractado
Fig . 1
Rayo
incidente
Rayo
refractado
Fig . 2
Elementos de una lente delgada. En todo problema de lentes delgadas
necesitamos conocer las siguientes características.

Centros de curvatura. Son los centros de las dos esferas que
determinan las caras de la lente y se representan con la letra “ C ”.

Eje de la lente. Es la recta que une a los centros de curvatura.

Radio de curvatura. Es la distancia del centro de curvatura a la cara
de la lente. Son dos radios de curvatura, el que traza la cara de la
izquierda se denomina “ R 1 ” y el que traza la cara derecha es “ R 2 ”.
176
R2
R1
C
C
C
C
R1
R2
Fig . 3

Plano de simetría. Es un plano normal al eje de la lente que la divide
simétricamente.

Centro óptico. Es el centro geométrico de la lente y resulta de l a
intersección del plano de simetría con el eje de la lente.

Distancia objeto. Es la distancia que hay del objeto al centro óptico
medida sobre el eje de la lente y se representa con la letra “ o ”.

Distancia imagen. Es la distancia que hay del punto del eje donde se
forma la imagen al centro óptico y se representa como “ i ”.

Foco. Una lente delgada tiene dos focos; El foco objeto que se define
como el punto del eje cuya imagen se forma en el infinito y el foco
imagen que se define como la imagen de un punto del eje que se
encuentra infinitamente alejado. El foco objeto lo ubicaremos a la
izquierda y el foco imagen a la derecha de la lente, estando ambos a la
misma distancia del centro óptico. Por comodidad los llamaremos
simplemente focos y los representaremos con la letra “ F ”.

Distancia focal. Es la distancia que hay del foco al centro óptico
medida sobre el eje de la lente y se representa con la letra “ f ”.
Características de la imagen. Vista la lente por el borde, la imagen se puede
formar a la izquierda o a la derecha. Al lado derecho de la lente se le denomina lado
real y al lado izquierdo como lado virtual, por tal motivo, si la imagen se forma del
lado izquierdo se dice que la imagen es virtual, y si se forma del lado derecho se dice
que la imagen es real. Dependiendo de la posición del objeto con respeco al centro
óptico y del tipo de lente, la imagen puede aparecer derecha o invertida y puede ser
mayor, menor o igual que el objeto.
177
Convenciones.

La luz siempre se considerará propagándose de izquierda a derecha.

El objeto siempre estará a la izquierda de la lente.

Para cualquier tipo de lente, la curva de la izquierda es trazada por
“ R 1 ”, y la curva de la derecha es trazada por “ R 2 ”, tal como se ilustra
en la Fig . 3 .
Convención de signos .
1.
La distancia del objeto “ o ” siempre será positiva.
2.
Cuando la imagen se forma a la derecha de la lente (imagen real), la
distancia “ i ” es positiva.
3.
Cuando la imagen se forma a la izquierda de la lente (imagen virtual),
la distancia “ i ” es negativa.
4.
El radio de curvatura a la izquierda de la lente es negativo.
5.
El radio de curvatura a la derecha de la lente es positivo.
R 2  
R1  
C
C
C
C
R1  
R 2  
Radio de curvatura negativo
Radio de curvatura positivo
Fig . 4
6.
La distancia focal “ f ” que corresponde al foco imagen (a la derecha
de la lente) es positiva   .
178
7.
La distancia focal “ f ” que corresponde al foco objeto (a la izquierda
de la lente) es negativa   .
TABLA DE CONVENCIONES
IZQUIERDA
LADO V IRTUAL
DERECHA
LADO V IRTUAL
RAYO INCIDENTE
RAYO REFLEJADO
i  
i  
R  
R  
f 
f  
o  
o  
Refracción en superficies esféricas. Nuestro objetivo es deducir una ecuación
que nos permita determinar la imagen que resulta cuando la luz procedente de un
objeto se refracta en una superficie esférica. Analicemos los triángulos de la Fig . 5 :
A





V
O
C
I
n1 n 2
R
Fig . 5
o
i
Del tiángulo OAC :           , de donde:
   
 A
Del triángulo A I C :           , de donde.
B 
  
Aplicando la Ley de Snell: n 1 sen   n 2 sen 
179
Suponemos que todos los triángulos son tan pequeños como se quiera, entonces
la Ley de Snell se puede escribir como n 1   n 2  , de donde.

n1 
C 
n2
Sustituyendo “  ” de C  en B  .
n1 

n2
D 

Sustituyendo “  ” de  A en D  .

n 1    
n2

n 2   n 1      n 2 

n1   n 2    n1  n 2

E 
Los ángulos “  ”, “  ” y “  ” se puedene expresar así.

Entonces.
AV
o

n 1  AV 
o

AV
R
n 2  AV 
i


n
1
AV
i
 n 2   AV 
R
Simplificando obtenemos.
n1
o

n2
i

n
1
 n2

R
1
Que es la ecuación buscada y donde:
o:
Es la distancia objeto.
i:
Es la distancia imagen.
n1 : Índice de refracción del medio donde está el objeto.
n 2 : Índice de refracción del medio donde se forma la imagen.
R : Radio de curvatura de la superficie esférica.
180
Ecuación del fabricante. Nuestro objetivo es deducir una ecuación que nos
permita calcular la d istancia focal en una lente delgada y que es conocida como la
ecuación del fabricante. Analizando la Fig . 6 .
R1
O
I'
1 n
R2
I
C1 C 2
n 1
Fig . 6
Aplicando
la
ecuación
de
refracción
de
superficies
esféricas
n 2 n 2  n1
1 a la superficie de la izquierda y haciendo n1  1, n 2  n e


o
i
R
i  i ' (porque la imagen es virtual), se obtiene.
n1
1 n n 1
 
o i'
R
 A
Ahora aplicamos la ecuación 1 a la superficie de la derecha en la Fig . 7 .
R2
O'
R1
C1
C2
I
n 1
i

o
Fig . 7
Y haciendo.
Se obtiene.
o '  i '
n1  n
n
1 n 1
 
i ' i
R2
n2  1
B 
Por ser una lente delgada   0 , entonces la ecuación B  se puede escribir.
n 1 n 1
 
i' i
R2
181
C 
Sumando las ecuaciones  A y C  .
1 n n 1
 
o i'
R1
n 1
n 1
 
i' i
R2
1 n n 1 n 1 n 1
   

o i' i' i
R1
R2
Obtenemos.
 1
1 1
1 
  n  1

R

o i
 1 R2 
2
Aplicando la ecuación 2 para calcular la distancia focal haciendo f  o . Por
definición, la imagen del punto focal está en el infinito, o sea i   , y por lo tanto
1
 0 , entonces la ecuación 2 se puede ecribir.
i
 1
1
1 
 n  1 

R

f
 1 R2 
3
Que es la ecuación buscada (ecuación del fabricante) y donde:
R 1 , R 2 : Son los radios de curvatura de la lente.
n : Es el índice de refracción de la lente.
f : Es la distancia focal.
Ecuación de las lentes delgadas. Combinando las ecuaciones
obtenemos:
1 1 1
 
o i f
2
y
3 ,
4
Ecuación que es conocida como la ecuación de las lentes delgadas y en la que,
como sabemos, “ o ” es la distancia objeto , “ i ” es la distancia imagen y “ f ” es la
distancia focal.
182
Aumento lateral. El aumento lateral “ M ” es la relación que existe entre las
alturas del objeto y la imagen. Nuestro objetivo es deducir las ecuaciones que nos
permitan calcular el aumento lateral y la altura de la imagen.
h
I
O
Fig . 8
h'
o
i
Los dos triángulos de la Fig . 8 son semejantes, por lo tanto
D 
i h'

o h
Al cociente
h h'
 , de donde.
o i
h
se le llama aumento lateral, por lo tanto.
h'
h'
E 
M
h
Sustituyendo “ M ” de E  en D  , tendremos que.
M
F 
i
o
Con el objeto de que “ M ” sea negativa cuando la imagen esté invertida,
incorporamos un signo   y la ecuación F  se escribe:
M 
5
i
o
183
Que es la primera ecuación buscada y en la que “ M ” se expresa en función de
la distancia objeto y de la distancia imagen. Conocido el aumento lateral podemos
h'
conocer la altura de la imagen recordando que M  , de donde.
h
h' M h
6
Que es la segunda ecuación buscada y en la cual “ h ” es la altura del objeto y
“ h ' ” es la altura de la imagen.
Potencia de una lente. Se le denomina potencia de una lente delgada a la
medida de su convergencia y es igual al inverso de su distancia focal,
matemáticamente se expresa.
P
7
1
f
Combinando las ecuaciones 7  y 3 , obtenemos.
 1
1 
P  n  1 

R

 1 R2 
8
Unidad de potencia en una lente. La unidad de potencia en una lente es la
dioptría, siempre que la distancia focal sea medida en metros. Por ejemplo, si la lente
tiene una distancia focal de 1 m , su potencia es la dioptría. Analizando la ecuación
7  puede verse que mientras más pequeña sea la distancia focal, mayor será la
potencia de la lente.
184
Construcción geométrica de imágenes. Conocida la posición del objeto con
respecto al centro óptico, se puede construir su imagen geométricamente con el trazo
de cualesquiera dos de tres rayos notables que son:
1.
2.
3.
El que llega a la lente paralelo al eje y se refracta pasando por el foco.
El que llega a la lente pasando por el foco y se refracta paralelo a él.
El que llega a la lente pasando por el centro óptico y sale de la lente
con la misma trayectoria.
F
C
F
O
I
Fig . 9
Dependiendo del tipo de lente y de la distancia objeto, los rayos notables al
refracterse divergen y las imágenes virtuales (a la izquierd a de la lente) se construyen
por la convergencia de sus prolongaciones.
F
I
O
C
F
Fig . 10

Lentes convergentes
Concepto de lente convergente.

Una lente convergente es aquella que refracta la luz y la hace
converger a un punto llamado foco. Hemos visto que una lente tiene
dos focos, pero el que a nosotros nos interesa es el foco imagen y al
cual le llamaremos simplemente foco.

En las lentes convergentes el foco está a la derecha de la lente.
185
Eje de
la lente
Fig . 1

Las lentes convergentes son más gruesas en el centro que en los
bordes.

La superficie de las lentes pueden ser esféricas, cilíndricas o una
combinación de ambas, y en algunos instrumentos de óptica las lentes
que se usan son porciones de paraboloides. (El análisis que se ha hecho
para las lentes delgadas, en general, se basa en superficies esféricas).
En la Fig . 2 se ilustran diversos tipos de lentes convergentes.
Fig . 2
Plano
Menisco
convexo
convergente
186
Biconvexo
Convenciones.

El objeto siempre estará a la izquierda de la lente, pero la distancia
objeto “ o ” siempre será positiva   .

Como en las lentes convergentes el foco está a la derecha de la lente,
la distancia focal “ f ” es poritiva   .

El radio de curvatura “ R 1 ”, por estar a la derecha de la lente, es
positivo   y “ R 2 ” es negativo   , obsérvese que “ R 1 ” y “ f ” están
del mismo lado.
R1  
F
Fig . 3
Determinación análitica de la imagen.

Conocido el índice de refracción y los radios de curvatura, se puede
calcular la distancia focal usando la ecuación del fabricante.
 1
1
1 
 n  1

R

f
 1 R2 

Conocida la distancia objeto y la distancia focal, se puede calcular la
distancia imagen con la ecuación de las lentes.
1 i 1
 
o i f
Si el valir de “ i ” es negativo significa que la imagen es virtual (aparece a l a
izquierda de la lente).
187

Conocida la distancia imagen se puede calcular el aumento leteral con
la ecuación.
M 

1
o
Conocido el aumento lateral se puede calcular la altura de la imagen
con la ecuación.
h' M h
Recuérdese que si “ M ” es negativo y, en consecuencia “ h ' ” resulta negativa,
significa que la imagen está invertida.
Construcción geoétrica de imágenes. Recuérdese que conocida la posición del
objeto con respecto a la lente se puede construir la imagen geométricamente con el
trazo de dos de tres rayos notables que son.
1.
2.
3.
El que llega a la lente paralelo al eje y se refracta pas ando por el foco
(foco imagen).
El que llega a la lente pasando por el centro óptico y sale de la lente
con la misma trayectoria.
El que llega a la lente pasando por el foco (foco objeto) y se refracta
paralelo al eje.
Las características de la imagen van a depender de la distancia del objeto a la
lente. En las figuras 4 a la 8 se ilustran los cinco casos posibles y las características
de la imagen.
1er caso :
oC
F
o
Imagen : Real
Invertida
h'  h
C F
Fig . 4
2o caso :
oC
h
C
o
F
F
Fig . 5
188
h'
Imagen : Real
Invertida
h'  h
3er caso :
C oF
h
o
C
F
F
h'
Fig . 6
Imagen : Real
Invertida
h'  h
4o caso :
oF
C
F
o
F
Fig . 7
No hay imagen
( Se forma en
el infinito)
5o caso :
oF
F
o
F
Fig . 8
189
Imagen : Virtual
Derecha
h'  h
Ejemplos.
1.
Una lente biconvexa con índice de refraccións 1.6 tiene un radio de curvatura
de 30cm . Calcular la distancia focal.
R1  
n  1.6
R 1  30 cm
Datos :
C
R 2  30 cm
R 2  
Despejamos “ f ” en la ecuación del fabricante y obtenemos.
f 
R1 R 2
n  1 R 2  R1 

30  30
1.6  1  30  30
f  25 cm
2.
Un objeto de 2 cm de alto se coloca a 6 cm de una lente boconvexa cuya
distancia focal es de 2 cm .
a)
Calcular la distancia imagen.
Datos :
n  1.6
R1  30 cm
1 1 i
 
i o f
 i
R 2  30 cm
6 2
o f

o f
62
i  3 cm
La imagen es real (está a la derecha de la imagen).
b)
Calcular el aumento lateral.
M 
c)
i
3

o
6
M  0.5
Calcular la altura de la imagen.
h '  M h   0.52 cm
h '  1 cm
190
El signo menos significa que la imagen está invertida.
o
F
3.
Una lente planoconvexa cuyo índice de refracción es 1.6 tiene un radio de
curvatura de 30 cm . Calcular la distancia focal.
a)
Si la luz incide sobre la cara plana.
R 2  
n  1.6
Datos :
R1  
R 2  30 cm
Despejamos “ f ” en la ecuación del fabricante y obtenemos.
1
f 
 1
1 


 R1 R 2 
n  1 

1
1.6  1  1  1 
   30 
f  50 cm
b)
Si la luz incide sobre la cara convexa.
R1  
n  1.6
Datos :
R 1  30 cm
R2  
191
f 
1
 1
1 


 R1 R 2 
n  1 

1
1.6  1 
1
1
 
  30  
f  50 cm
Las distancias focales objeto e imagen son iguales.
Ejercicios.
1.
Un objeto colocado frente a una lente biconvexa produce una imagen virtual a
6 cm de la lente con un aumento de 1.2 . El índice de refracción de la lente es de 1.6 y
los radios de curvatura son iguales.
a)
Calcular la distancia objeto.
b)
Calcular la distancia focal.
c)
Calcular el valor del radio de curvatura.
2.
Un objeto colocado frente a una lente biconvexa produce una imagen vir tual a
5 cm de la lente con un aumento de 1.25 . Los radios de curvatura de la lente miden
24 cm . ¿cuál es el índice de refracción de la lente?
3.
Frente a una lente biconvexa con una distancia focal de 3 cm se coloca un
objeto de 2 cm de altura. Determinar gráfica y analíticamente las características de la
imagen para las siguientes distancias objeto: 2 cm, 3 cm, 4 cm, 6 cm y 12 cm .

Lentes divergentes
Concepto de lente divergente.

Una lente divergente es aquella que refracta la luz y la hace divergir
como si procediera de un punto llamado foco. Hemos visto que una
lente tiene dos focos, pero el que ahora nosotros nos interesa es el foco
objeto, el cual denominaremos simplemente como foco.

En las lentes divergentes, el foco está a la izquierda de la lente.
192
F
Fig . 1
De acuerdo con la Fig . 1 , los rayos que llegan paralelos al eje de la lente se
refractan y divergen como si procedieran de un punto llamado foco.

Las lentes divergentes son más delgadas en el centro que en los bordes.

En las lentes divergentes siempre se obtiene una imagen virtual y
derecha. En la Fig . 2 se ilustran diversos tipos de lentes divergentes.
Fig . 2
Bicóncavo
Plano cóncavo
Menisco
divergente
193
Convenciones.

El objeto siempre estará a la izquierda de la lente, pero la distancia
objeto “ o ” siempre será positiva   .

Como en las lentes divergentes el foco está a la izquierda de la lente,
la distancia focal “ f ” es negativa   .

El radio de curvatura “ R 1 ” por estar a la izquierda de la lente, es
negativo   y “ R 2 ” es positivo   , obsérvese que “ R 1 ” y “ f ” están
del mismo lado.
R1 
F
Fig . 3
Determinación analítica de la imagen.

Conocido el índice de refracción y los radios de curvatura se puede
calcular la distancia focal usando la ecuación del fabricante.
 1
1
1 
 n  1 

R

f
 1 R2 
Conocida la distancia objeto y la distancia focal se puede calcular la distancia
imagen con la ecuación de las lentes.
1 i 1
 
o i f
Si “ i ” es negativa, significa que la imagen es virtual (aparece a la izquierda de
la lente).
194

Conocida la distancia imagen se puede calcular el aumento lateral con
la ecuación.
M 

i
o
Conocido el aumento lateral se puede calcular la altura de la imagen
con la ecuación.
h' M h
Es necesario recordar que si la imagen es virtual.

“ i ” es neagativo.

“ M ” es positivo.

“ h ' ” es positiva.
Lo que significa que la imagen está derecha.
Construcción geométrica de imágenes. Conocida la posición del objeto con
respecto a la lente se puede construir la imagen geométricamente con el trazo de dos
de tres rayos notables que son:
1.
El que llega a la lente paralelo al eje y se refracta como si procediera
del foco (foco objeto).
2.
El que llega a la lente pasando por el centro óptico y sale de la lente
con la misma trayectoria.
3.
El que llega a la lente en la dirección del foco (foco imagen) y s e
refracta paralelo al eje.
1
F
F
2
Fig . 4
3
195
La imagen que se obtiene en una lente divergente siempre es virtual, derecha y
más pequeña que el objeto; el tamaño de la imagen aumenta a medida que el objeto se
acerca a la lente.
F O2 I 1 I 2
O1
Fig . 5
Ejemplos.
1.
Una lente planocóncava cuyo índice de refracción es 1.5 tiene un radio de
curvatura de 40 cm . Calcular la distancia focal.
a)
Si la luz incide por la cara plana:
R 2  
n  1.5
Datos :
R1  
R 2  40 cm
f 
1
 1
1 


 R1 R 2 

n  1 
1
1.5  1  1  1 
  40 
f  80 cm
El foco está a la izquierda de la lente.
196
b)
Si la luz incide por la cara cóncava.
n  1.5
Datos :
R 1  40 cm
R2  
R1 
1
f 
 1
1 


 R1 R 2 

n  1 
1
1.5  1 
1
1
 
  40  
f  80 cm
El foco está a la izquierda de la lente. Las distancia focales objeto e imagen
son iguales.
2.
Un objeto de 2 cm de alto se coloca a 6 cm de una lente bicóncava cuya
distancia focal es de 2 cm .
a)
Calcular la distancia imagen.
Datos :
h  2 cm
1 1 1
 
o i f
o  6 cm
f  2 cm
of
6  2
 i

o  f 6   2
i  1.5 cm
La imagen es virtual (está a la izquierda de la lente).
b)
Calcular el aumento lateral.
M 
c)
i
 1.5

o
6
M  0.25
Calcular la altura de la imagen.
h '  M h  0.252 cm
h ' 0.5 cm
197
d)
Determinar gráficamente las características de la imagen.
O
F I
Ejercicios.
1.
Un objeto colocado frente a una lente bicóncava produce una imagen a 24 cm de
la lente con un aumento de 0.6. El índice de refracción de la lente es 1.6 y los radios
de curvatura son iguales.
a)
b)
c)
Calcular la distancia objeto.
Caclular la distancia focal.
Calcular el valor del radio de curvatura.
2.
Un objeto colocado frente a una lente bicóncava produce una imagen a 24 cm de
la lente con un aumento de 0.4. Los radios de curvatura de la lente miden 52 cm . ¿cuál
es el índice de refracción de la lente?
3.
Frente a una lente bicónava con una distancia focal de 9 cm se coloca un objeto
de 2 cm de altura. Determinar gráfica y analíticamente las características de la
imagen cuando el objeto se coloca a 6 cm y a 9 cm de la lente.
198
Instrumentos ópticos

Ojo humano
Constitución del ojo humano. El ojo humano es el órgano en el cual reside el
sentido de la vista. El ojo es un conjunto de musculosa, membranas y humores que
interactúan entre si formando un sistema llamado globo ocular.
Cristalino
Esclerótic a
Retina
Córnea
Línea virtual
Eje
Fóvea
Humor
ocular
Papila
Humor
acuoso
Iris
vítreo
Vaina de
Fig. 1
 Nervio

 óptico
nervio óptico
El globo ocular tiene forma aproximadamente esférica de unos 2.5 cm de
diámetro y está formado, básicamente por tres membranas: la esclerótica, la coroides
y la retina. En el interior de las membranas se encuentran los medios transparentes
que son: el humor acuoso, el cristalino y el humor vítreo.
La esclerótica. Es una membrana de color blanco que constituye propiament e
la envoltura del globo ocular. Por la parte posterior tiene un orificio por donde pasa
el nervio óptico, por la parte frontal modifica su curvatura y se vuelve transparente
constituyendo la córnea.
La coroides . Es una menbrana que tapiza toda la cara interna de la esclerótica
y está formada por dos hojas entre las cuales se encuentran los vasos sanguíneos que
nutren el globo ocular. Las dos hojas de la coroides están recubiertas de pigmento
negro que convierten el interior del globo ocular en una cámara oscura. Hacia el
frente la coroides se modifica formando el iris y los cuerpos ciliares, los cuales están
constituidos por los procesos ciliares y por las fibras de los músculos ciliares. Los
procesos ciliares sirven de apoyo a las fibras zonulares que sostienen al cristalino.
Frente al cristalino la corioides se modifica formando el iris, que es el disco
vertical que tiene en el centro un orificio al cual se le denomina pupila. El pigmento
que posee el iris es el que determina el color de los ojos.
199
Los músculos ciliares son músculos lisos ordenados en una estructura radial
que conforma el disco del iris y cuya contracción o relajación determina que se
agrande o empequeñezca la pupila. De este modo los músculos ci liares hacen que el
iris se comporte como un diafragma que se abre o se cierra dependiendo de la
intensidad de la luz.
La retina es la tercera menbrana del globo ocular, es una membrana
transparente e incolora que tapiza el interior de la coroides y está i ntegrada por
neuronas de diferentes tipos y ordenadas en tres capas:
1a
Está integrada por neuronas sensoriales de dos tipos llamadas conos y
bastones.
2a
Está formada por células bipolares.
3a
Formada por neuronas ópticas que convergen en la pupila para formar
el nervio óptico.
La papila es una depresión de la retina y es el punto por donde las fibras
nerviosas salen del globo ocular para formar el nervio óptico y por donde salen los
vasos sanguíneos que irrigan el globo ocular. En la papila no hay conos ni bastone s y,
por lo tanto, no hay visión, por lo que se le denomina punto ciego .
Otra depresión que existe en la retina es la fóvea también se llama fovea
centralis, mácula lútea o mancha amarilla) y es una zona formada por conos. Con
iluminación ordinaria en la f óvea, la agudeza visual es 20 veces mayor que en el resto
de la retina.
El humor acuoso es un líquido transparente que llena el espacio comprendido
entre la córnea transparente y el iris.
El cristalino está formado por una cutícula transparente y fibrosa q ue es dura
en el centro y progresivamente se va haciendo más blanda hacia la superficie. El
cristalino está sujeto por las fibras zonulares a los cuerpos ciliares y se sostiene en su
lugar por la presión que sobre él ejercen el humor acuoso y el humor vítr eo.
El humor vítreo es un líquido transparente de aspecto gelatinoso con una
constitución química muy parecida a la del humor acuoso y llena la mayor parte del
globo ocular detrás del cristalino.
200
Funcionamiento del ojo humano . Hemos visto que en la retina existen dos
tipos de neuronas sensoriales llamadas conos y bastones. El proceso de la visión suele
dividirse en dos etapas.
1a
La formación de la imagen en la retina por la luz que le llega al objeto.
Al parecer, la función de los conos y bastones es transformar los
estímulos luminosos en impulsos eléctricos.
2a
En el cerebro se realiza el proceso de integración de la visión por la
interpretación de los impulsos que le llegan a la retina a través del
nervio óptico.
Parece ser que la función de los conos e spercibir los objetos luminosos, así
como los colores. Así mismo, los bastones parecen estar incapacitados para registrar
los colores y en cambio son sensibles para percibir objetos poco luminosos, al
movimiento y a variaciones ligeras de intensidad.
Es en la fóvea de cada uno de los ojos donde se nfoca la imagen del objeto que
deseamos ver, para esto, los músculos que controlan el movimiento del ojo orientan el
globo ocular hasta que dicha imagen cae sobre la fóvea; en el resto de la retina solo
se forma un cuadro general de la visión, pero los objetos que se encuentran en él no
se distinguen. En cambio, cuando el ojo se ha adaptado a la oscuridad puede ver
mejor con el resto de la retina que con la fóvea.
Cuando hay variaciones de brillo en el campo visual , en la pupila se realiza un
proceso llamado adaptación: si el brillo del campo disminuye, la pupila se dilata y si
el brillo del campo aumenta, la pupila se contrae regulando la entrada de la luz.
Pero por una parte, la pupila puede aumentar de tamaño solo 16 veces (lo que
significa que su diámetro puede aumentar a cuarto veces su tamaño inicial), y por
otra parte, el ojo puede adaptarse a variaciones de brillo de hasta 100 000 veces. Una
variación tan grande en el brillo del campo visual no puede ser compensada por una
variación en el área de la pupila, siendo necesario que el mecanismo receptor de la
retina realice por sí mismo el proceso de adaptación a grandes variaciones de brillo.
Los medios transpar entes del ojo se comportan como un sistema óptico formado
por tres lentes: la primera es una lente plana convexa y corresponde al humor acuoso,
la segunda es una lente biconvexa y corresponde al cristalino, y la tercera es una
lente cóncavo convexa y corre sponde al humor vítreo.
Cristalino
Humor vítreo
biconvexa
cóncavoconvexa
Humor acuoso
planoconvexa
Fig . 2
201
Este sistema óptico proyecta en la retina una imagen in vertida y menor que el
objeto.
Fig . 3
Los rayos de luz que proceden de un objeto situado en el infinito (más alla de
6 m de distancia) son paralelos y al ser refractados por el sistema ópt ico del ojo
convergen en el foco, formándose la imagen en la retina de un ojo normal. Los rayos
de luz procedentes de un objeto cercano son divergentes, pero al ser refractados por
el sistema óptico del ojo también convergen en el foco, formándose la image n en la
retina del ojo normal. El proceso de adaptación del globo ocular que le permite
enfocar objetos lejanos y cercanos se denomina acomodación. Se considera que el ojo
podría lograr la acomodación de tres maneras.
1a
Haciendo que la retina se acerque o se aleje.
2a
Que el cristalino se acerque o se aleje de la retina.
3a
Que la convexidad del cristalino se modifique.
Se sabe que en ojo humano solo ocurre la tercera posibilidad. Esta modificación
es realizada por la acción de las fibras zonudales y por los músculos ciliares que se
relajan o se contraen para hacer al cristalino más o menos convexo.
Con la edad el cristal ino va perdiendo flexibilidad y, por lo tanto, se va
perdiendo la capacidad de acomodación. A esta deficiencia se le conoce con el
nombre de presbicia.
Defectos visuales. Se le llama defecto de la visión a la deficiencia funcional
del globo ocular. Algunos como el daltonismo son de carácter genético, otros como la
diplopía obedecen a una deficiencia muscular externa al globo ocular. Otros en
cambio obedecen a trastornos metabólicos como son las cataratas y los cambios de
refringencia de los humores. Sin emb argo hay algunos defectos de la visión que se
deben a una relajación incorrecta entre la retina y los medios transparentes del ojo.
Los rayos de luz que llegan paralelos al eje ocular convergen en el foco. Si el
foco cae sobre la retina formando en ésta la imagen de un objeto que se encuentra en
el infinito se dice que el eje es normal o emétrope, de no ser así se dice que el ojo es
amétrope. Dos formas sencillas de ametropía son la miopía y la hipermetropía.
202
En un ojo miope el globo ocular es demasiado la rgo con respecto a la curvatura
de la córnea y entonces el foco del sistema óptico se encuentra delante de la retina.
Otra forma de decirle es que el sistema óptico de un ojo miope produce demasiada
convergencia de los rayos paralelos al eje ocular y éstos convergen en un punto
(foco) que se encuentra delante de la retina.
En un ojo hipermétrope el globo ocular es demasiado corto con respecto a la
curvatura de la córnea y, entonces, el foco del sistema óptico se encuentra atrás de la
retina. Otra forma de d ecirlo es que el sistema óptico de un ojo hipermétrope no
produce la suficiente convergencia de los rayos paralelos al eje ocular y éstos
convergen en un punto (foco) que se encuentra atrás de la retina.
Fig . 4
El astigmatismo es un defecto visual motivado porque la superficie de la
córnea no es esférica, teniendo sus meridianos una curvatura diferente y, en
consecuencia, los rayos de luz que llegan paralelos al eje ocular a través de planos
diferentes experimentan convergencias diferentes.
Fig . 5
En el ojo astigmático de la Fig . 5 la curvatura de la córnea en un plano permite
que los rayos que llegan paralelos al eje ocular tengan la convergencia correcta y el
foco se encuentra en la retina. Pero al cambiar el plano de curvatura de la córnea se
diferente y la convergencia de los rayos es insuficiente por lo que convergen en un
punto (foco) localizado atrás de la retina.
Corrección de los defectos visuales.
a)
Miopía. Hemos visto que en un ojo miope el foco del sistema óptico
se encuentra delante de la retina debido al alargamiento del globo
ocular. Este defecto de la visión se corrige colocando delante del eje
una lente divergente.
203
El efecto de la lente divergente es disminuir la co nvergencia de los
rayos que llegan paralelos al eje ocular, de modo que el foco se desplaza
hacia atrás coincidiendo con la retina.
Fig . 6
b)
Hipermetropía. En un ojo hipermétrope, el foco del sistema óptico se
encuentra atrás de la retina debido a que el globo ocular es demasiado
corto con respecto a la curvatura de la córnea. Este defecto de la
visión se corrige colocando delante del ojo una lente convergente.
El efecto de la lente convergente es aumentar la convergencia de los
rayos que llegan paralelos al eje ocular, de modo que el foco se desplaza
adelante coincidiendo con la retina.
Fig . 7
c)
Astigmatismo. Es un defecto visual originado por una diferencia de
curvatura en los meridianos de la córnea. Este defecto se corrige
colocando delante del ojo una lente cilíndrica convergente.
El efecto de esta lente es aumentar la convergencia de los rayos que
llegan paralelos al eje ocular a través del plano donde la curvatura de l a
córnea hace que el foco esté atrás de la retina, de modo que dicho foco se
desplace hacia adelante coincidiendo con la retina, así se obtiene la
convergencia correcta en cualquier plano, ya que la refracción en los planos
donde la curvatura es correcta no es modificada por la lente.
a 
Fig . 8
204
b 
b '
a '
Fig . 8

Cámara fotográfica
Construcción de la cámara fotográfica. Esencialmente, la cámara fotográfica
es una cámara oscura prevista de un objetivo en una de su s caras y de una película en
la cara opuesta. El dispositivo se complementa con un diafragma que regula la
cantidad de luz que debe llegar a la película y de un obturador que permite el pase de
la luz en el momento deseado por el fotógrafo.
La película es una cinta delgada de material plástico cubierta por una emulsión
fotosensible. Una vez impresionada la película, es sometida a un tratamiento químico
llamado revelado, constituyendo el negativo que ha de usarse para la impresión en
papel.
El objetivo es un a lente o conjunto de lentes que capta la luz procedente del
objeto y la dirige al ocular o a la película, formando ésta una imagen invertida y más
pequeña que el objeto.
El ocular es una lente o sistema de lentes que se antepone al eje y cuya función
es permitirle al fotógrafo hacer el encuadre correcto. La luz procedente de los objetos
que se encuentran frente a la cámara y que es captada por el objetivo forma en el
ocular la imagen del campo visual. El fotógrafo, al hacer el encuadre delimita el
campo visual que desea abarcar en la toma.
Objetivo
Fig . 1
Película
Cámara oscura
Funcionamiento de la cámara fotográfica. Tal funcionamiento es similar al
del ojo humano: El objetivo equivale al sistema ocular del eje, la película a la retina,
el diagrama al iris y la abertura del diafragma a la pelí cula. Los ajustes previos a la
impresión de la película son: Enfoque, Abertura y Velocidad.
El
paralelos
película,
correcto,
enfoque consiste en regular la convergencia de los rayos que llegan
al eje del objetivo a efecto de que la imagen se forme con nitidez en la
esto se consigue deslizando sobre su eje las lentes del objetivo. El enfoque
así como el encuadre, se pueden apreciar a través del ocular.
205
La abertura depende del diafragma, cuya función es regular la cantidad de luz
que debe pasar a la cámara os cura. Si la luz es muy intensa la abertura del diafragma
deberá ser pequeña, y su hay poca luz, la abertura será ser grande pues la cantidad de
luz excesiva o deficiente puede perjudicar a la exposición.
Y el término velocidad se refiere a qué tan rápido v uelve a cerrarse el
obturador una vez accionado, lo que equivale a determinar el intervalo de tiempo
durante el cual la luz estará impresionando a la película. La velocidad debe ser
función de la intensidad de la luz, de la abertura del diafragma o de ambo s.
Por ejemplo, si la luz es muy intensa o la abertura del diafragma es grande, la
velocidad también deberá ser grande, pues de lo contrario pasará luz por demasiado
tiempo y la toma saldrá sobreexpuesta. Si por el contrario hay poca luz o la abertura
del diafragma es muy pequeña, la foto deberá a muy poca velocidad, pues de lo
contrario no pasará la suficiente luz y la toma saldrá subexpuesta.

Filtro óptico
Concepto y utilidad del filtro óptico. Los filtros ópticos son lentes especiales
que se anteponen al objetivo de un instrumento óptico y su finalidad es eliminar
algunas de las radiaciones del espectro, dejando pasar a los otros.
Tipos de filtros ópticos. Algunos filtros se usan para corregir las deficiencias
de las emulsiones, por ejemplo, los de tinte amarillo que sirven para mejorar las
fotografías hechas con emulsiones ortocromáticas (emulsiones fotográficas sensibles
a todos los colores del espectro comprendidos entre el amarillo y el violeta).
Algunos filtros se usan para obtener efectos artísticos , por ejemplo, los filtros
rojos con los que se obtienen cielos oscuros sobre los que destacan las nubes blancas.
Los filtros infrarrojos solo permiten que la emulsión sea impresionada por los rayos
infrarrojos. Los llamados filtros de Word solo permiten que la emulsión sea
impresionada por los rayos ultravioleta. Los filtros polarizantes polarizan la luz
eliminando los reflejos de los cristales o de otros objetos brillantes a los que se desea
retratar u observar. Algunos filtros sirven para atenuar los col ores excesivamente
dominantes como el azul en el horizonte marino o el rojo que predomina al amanecer
o al atardecer.
Para tomar fotografías con luz artificial usando una película para luz de día se
usa un filtro azul claro, o para tomar fotografías a la luz del día usando una película
para luz artificial se usa un filtro anaranjado pálido.
206
COMPETENCIA PARTICULAR 3.
Reconocer y com prender los conceptos, principios y leyes fundam entales de la física
m oderna para identificar los fenóm enos correspondien tes a física relativista y m ecánica
cuántica, de tal m anera que aplique estos conocim ientos en el área tecnológica y en su
vida cotidiana.
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No.1
Com prender los conceptos, principios y leyes fundam entales de al Física Moderna para
identificar los fenóm enos correspondientes a la física relativista.
UNIDAD # 3 DEL PROGRAMA: FISICA MODERNA
ACTIVIDADES
DE APRENDIZAJE




DE ENSEÑANZA
Identificara mediante un trabajo de
investigación bibliográfica o de
Internet los postulados de la Física
Relativista.
Identificar los postulados de la
relatividad basados en la teoría de
Einstein.
Explicar la relación entre la teoría
general y la especial en las
transformaciones y los marcos de
referencia en movimiento inicial y
acelerado.
Reconocer la mediación de un
evento y relaciona a este con las
coordenadas espacio – tiempo.
207





Organizar a los alumnos en grupos
colaborativos para unificar la
información aportada.
Mediante la técnica de exposición
explicar los postulados de la Física
Relativista basada en la teoría de
Einstein.
Aplicar los modelos matemáticos de
las ecuaciones de transformación de
la masa longitud y tiempo.
Organizar a los alumnos en equipos
colaborativos para la resolución de
ejercicios y verifica el resultado.
Proporcionar de forma sofisticada un
listado de ejercicios del tema en
estudio.
RESULTADO DE APRENDIZAJE PROPUESTO (RAP) No.2
Conocer y com prender los conceptos, principios y leyes fundam entales de la física
m oderna para identificar los fenóm enos correspondientes a la física cuántica.
ACTIVIDADES
DE APRENDIZAJE





DE ENSEÑANZA
Analizar el video de radiación
(cuerpo negro) teniendo una sesión
de preguntas y respuestas.
Elaborar un resumen utilizando un
instrumento de aprendizaje.
Atiende a la solución de problemas
propuestos por el profesor y expone
sus dudas.
Resolver problemas propuestos por
el profesor utilizando los modelos
matemáticos vistos en clase.
Realizar la resolución de una lista
de problemas propuestos por el
profesor en forma extraclase.





208
Mediante la técnica de exposición y
con apoyo de un video, explicar el
fenómeno de la radiación delcuerpo
negro.
Moderar la discusión y debate sobre
lo expuesto en el video.
Analizar los modelos matematicos de
la radiación, atomo cuantico, teoría
cuántica, particula – onda, partículas
elementales,
antipartícula
y
antimateria, radioactividad, fusión y
fusión nuclear.
Ejemplificar la aplicación de los
modelos matematicos de los temas
mencionados en la resolución de
ejercicios.
Proporcionar de forma dosificada una
lista de ejercicios.