SOLUCIÓN Problemas 1
Anuncio
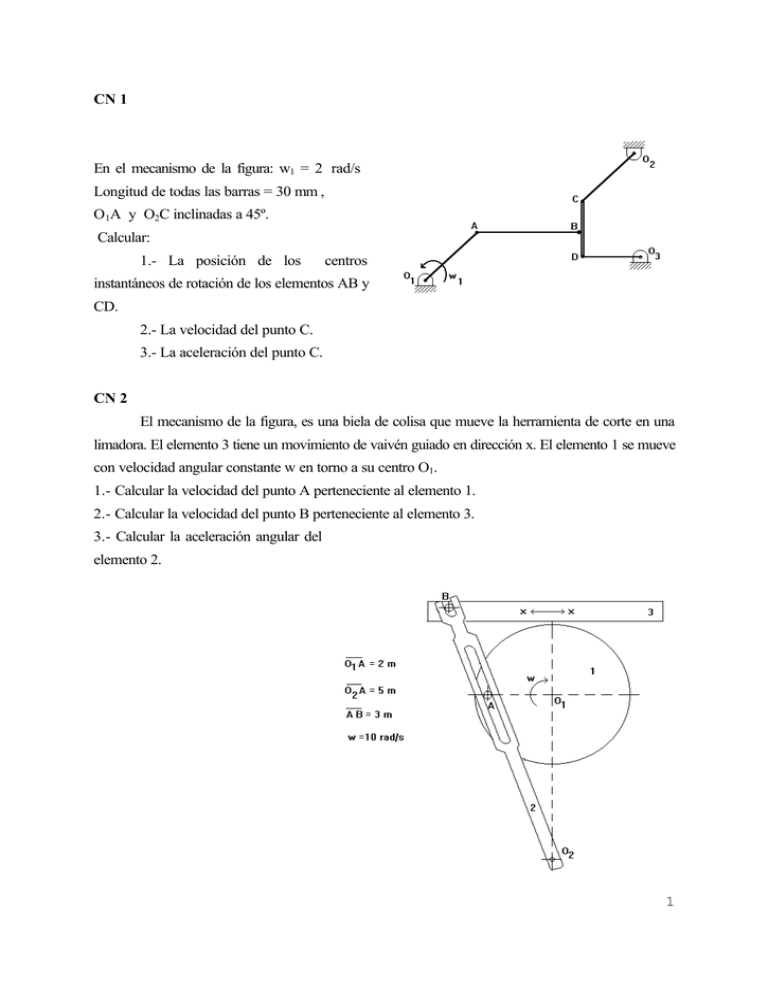
CN 1 En el mecanismo de la figura: w1 = 2 rad/s Longitud de todas las barras = 30 mm , O1A y O2C inclinadas a 45º. Calcular: 1.- La posición de los centros instantáneos de rotación de los elementos AB y CD. 2.- La velocidad del punto C. 3.- La aceleración del punto C. CN 2 El mecanismo de la figura, es una biela de colisa que mueve la herramienta de corte en una limadora. El elemento 3 tiene un movimiento de vaivén guiado en dirección x. El elemento 1 se mueve con velocidad angular constante w en torno a su centro O1. 1.- Calcular la velocidad del punto A perteneciente al elemento 1. 2.- Calcular la velocidad del punto B perteneciente al elemento 3. 3.- Calcular la aceleración angular del elemento 2. 1 CN 3 En el mecanismo de la figura: R = 50 mm r = 40 mm w = 10 rad /s a = 20 rad /s2 c = 100 mm - Calcular la velocidad VB - Calcular la aceleración AB CN 4 En el mecanismo de la figura el elemento 1 gira en torno al punto A. A.1.- Calcular la posición del centro instantáneo de rotación del elemento 2. A.2.- Construir el cinema de velocidades del elemento 2 y representar de forma aproximada en el cinema la velocidad del punto E. R2 A.3.- Calcular la velocidad de deslizamiento en B.1.- V3 D el punto de contacto C. Construir el cinema de aceleraciones del elemento 2. Representar de forma aproximada la posición del E a3 3 R2 polo de 2 aceleraciones del elemento 2 . C w1 = 2 rad/s R1 = 2 m V3 = 2 m/s a 1 = 4 rad/s2 R2 = 4 m a3 = 4 m/s2 B A CN5 En el mecanismo de la figura la barra ABC es un o1 R1/2 "1 R1 1 2 único sólido rígido. Se conoce la velocidad VA cuyo módulo es 17 m/s y la aceleración del punto B cuyo módulo es 15 m/s2 La escala del dibujo es aproximadamente 1:1000 1.- Cuantos grados de libertad tiene el mecanismo? . Justificar la respuesta. 2.- Determinar las posiciones de los centros instantáneos de rotación de todos los elementos del mecanismo. 3.- Determinar la velocidad del punto G. 4.- Determinar la aceleración del punto D. G E 3 D 4 F C aB 2 1 B VA A 3 CN6 D 3 A 1 B 2 C P1.- ¿ Cuantos grados de libertad tiene el mecanismo de la figura ?. Justificar la respuesta. P2.- El alumno se propondrá a sí mismo y resolverá gráficamente el problema. Para ello: - Debe formular ANALÍTICAMENTE las ecuaciones de excitación aplicadas a los elementos que estime más convenientes. Formulará ecuaciones de excitación en el número necesario y suficiente para que el mecanismo quede cinemáticamente determinado. Se recomienda formularlas de la forma más sencilla posible a la vista de P3. Indique de forma clara y precisa CUANTAS Y CUALES son las ecuaciones de excitación. - Es condición obligatoria, sin embargo, que alguna de las barras del mecanismo se mueva. P3.- El alumno resolverá GRAFICAMENTE el problema que él mismo se ha propuesto en P2. Calculando velocidades y aceleraciones en todos los puntos significativos del mecanismo así como velocidades angulares y aceleraciones angulares en los tres elementos del mecanismo. NOTA: Se debe explicar de forma clara y completa toda la resolución gráfica, indicando claramente las ecuaciones que soportan las resoluciones gráficas , las posibles direcciones de vectores etc 4 SOLUCIÓN CN1 Cálculo de velocidades: VA = w1.O1A = 2.30= 60 mm/s Resolviendo gráficamente mediante el método de las velocidades proyectadas: VAP = VA . cos 45º = 42,43 mm/s AIAB = 42,55 mm BIAB = 67,5 mm CICD = 42,426 mm BICD = 33,54 mm wAB = VA/AIAB = 1,41 rad/s VB = wAB BIAB = 95,2 mm/s wCD = VB/AICD = 2,84 = w3 VC = wCD CICD = 120,4 mm/s w2 = VC/CO2 = 4 rad/s Cálculo de aceleraciones: aA = aAn = w12.O1A = 4.30 = 120 mm/s2 aI = aCn + aCt + aICn + aICt aCn = w22 . 30 = 480 mm/s2 aICn = wCD2 . CICD = 342 mm/s2 aI = aDn + aDt + aIDn + aIDt aDn = w32 . 30 = 242 mm/s2 5 aIDn = wCD2 . DICD = 242 mm/s2 Gráficamente se obtiene aI = 844 mm/s 2 aB = aI + aBIn + aBIt aBIn = wCD2 . BICD = 270,5 mm/s2 aB = aA + aBAt + aBAn aBAn = wAB 2 . 30 = 59,6 mm/s2 aC = aB + aCBn + aCBt aCBn = wCD2.15 = 121 mm/s2 aC = aCn + aCt aCn = w22.30 = 480 mm/s2 aI aB aC 6 SOLUCIÓN CN2 1.- |VA |= w. O1A = 20 m/s 2.- sen a = 2/5 ; a = 23,57º |VA2 |= |VA |. sena = 20 . 2/5 = 8 m/s |VA21 |= |VA |. cosa = 20 . 0.916 =18,32 m/s w2 = |VA2|/AO 2 = 8/5 = 1.6 rad/s VA1 V A12 V B2 B |VB2 |= w2 . O2B = A VA2 V B32 VB3 8/5 . 8 = 12.8 7 m/s |VB3 |= VB2 / cosa = 12.8 / 0.916 = 13.97 m/s 3.- Aceleraciones. Consideramos un sistema de referencia móvil situado en A2 de forma que la aceleración relativa es paralela a O2A. aA1 = arel + aarr + acor = aA1n 2 aarr = aA2 = aA2n + aA2T 2 |aA2n |= w2 . O2A = 12.8 m/s acor = 2 w2 x VA12 |acor |= 2 . 1,6 . 18,32 =58,62 m/s2 |aA1n |= w12 . O1A = 100 . 2 = 200 m/s2 |aA2T |= a 2 . O2A = 123 m/s2 en el cinema a 2 = 24.6 rad/s2 VA12 acor w acor aA2n aA2t arel aA1 8 SOLUCIÓN CN3. VA = w.IA = 10 . 64,03 = 640,3 mm/s VB= 400 mm/s IA = 64,03 mm wAB = VAB /AB = 500/100 = 5 rad/s aI = w2 . R = 100.50 = 5000 mm/s2 OI / O' I' = OA/O'A' 2 aO = a.R = 20.50 = 1000 mm/s O'A' = OA . O' I' / OI = 40.51/50 = 40,8 mm aB = aA + aBAn + aBAt aA = 3200 mm/s2 aBAn = wAB 2 . AB = 52 . 100 = 2500 mm/s2 aB = 3400 mm/s 2 9 SOLUCIÓN CN4 A.1 VB VD V3 D V3 3 4m I2 4m VB A IBD B Puesto que la distancia entre los puntos B y D permanecerá invariable para cualquier posición del mecanismo, se puede considerar el sólido imaginario BD con lo que el mecanismo equivalente resulta ser un cuadrilátero articulado cuyo extremo 3 puede deslizarse horizontalmente. |VB| = w1 . R1/2 = 2.2/2 = 2 m/s A.2 CINEMA DE VELOCIDADES E’ La figura muestra el cinema de velocidades del VB elemento 2. Utilizamos un factor de escala igual a 2. VD A.3.- Para el cálculo de la velocidad de deslizamiento en D’ P V3 10 el punto C, utilizamos el centro instantáneo de rotación del elemento 2 calculado anteriormente. La velocidad de deslizaiento, tendrá una dirección tangente al contacto entre los dos elementos. V C12 V C2 VC1 I2 C A B |VC2 |= |V3 |= 2 m/s dirección y sentido indicados. Los módulos de |VC2| y|V3 |son iguales porque sus distancias a I2 son iguales. La dirección de VC1 es perpendicular a la recta AC. El factor de escala utilizado ahora es aproximadamente 1. B.- ACELERACIONES a3 aDBN aBN aDBT aB aB aBT aD aBDN aBDT 11 Calculamos en primer lugar la aceleración aB mediante sus componentes normal y tangencial. |aBN |= w12 . R1/2 = 4.2/2 = 4 m/s2 |aBT |= a . R1/2 = 4.2/2 = 4 m/s2 Pasamos ahora a calcular aD aD = aB + aDBN + aDBT aD = a3 + aD3N + aD3T |aDBN |= wDB 2 . DB = 1/9 . 6 = 2/3 m/s2 |aD3N |= w22 . R2 = 1/4 . 4 = 1 m/s2 |wDB |= |VB |/ BIBD = 2/6 = 1/3 rad/s |w2 |= |V3 |/ R2 = 2/4= 1/2 rad/s CINEMA DE ACELERACIONES Q a3 aD D’ E 12 SOLUCIÓN CN 5: 1.- n = 4 +1 = 5 elementos Restricciones = 3 + 2x4 + 3x1 = 14 k= 5x3 - 14 = 1 gdl 2.- I3 G E 3 D 4 I2 C F I4 2 1 I1 B A 13 I3 G E VG 3 D 4 VF I2 I4 F C 2 1 I1 B VC VA A 3.- Cálculo de VG w1 = |VA | / I1A = 17/23 = 0.74 rad/s VC = w1 . I1C = 0.74 * 71 = 52.5 m/s dirección perpendicular a I1C , sentido indicado. w2 = |VC | / I2C = 52.5/35 = 1.5 rad/s VF = w2 * I2F = 1.5 * 16 = 24 m/s w4 = |VF | / I4F = 24/14 = 1.71 rad/s VG = w4 * I4G = 1.71 * 32 =54.8 m/s VD = w2 * I2D = 1.5 * 39 = 58.5 m/s w3 = |VD | / ED = 58.5 / 32 = 1.82 rad/s 14 4.- Cálculo de aD G E 3 D 4 F 2 C aB 1 C’ aABn B B’ VA aB aC a ABt A aB A’ aA aA aA = aB + aABn + aABT |aABn |= w12 * AB = 0.742 * 36 = 19.71 m/s2 La dirección de aA es obligatoriamente horizontal debido a su restricción. Obtenemos aC mediante el cinema de aceleraciones del elemento 1 aD = aC + aDCn + aDCt |aDCn | = w22 . DC = 1.52 * 35 = 78.75 m/s2 aD = aDn + aDt |aDn | = w32 . ED = 1.822 *32 = 106 m/s2 |aD | = 145 m/s2 aproximadamente a escala en el cinema. 15 C’ aDn B’ aC aB A’ aA aDt aD aDCn aDCt 16 SOLUCION CN6 P1.- Consideramos juntas compuestas revolución-traslación en B y C. Nº de elementos del mecanismo = 3 móviles + tierra = 4 GDL si no hubiese restricciones = 4 * 3 = 12 Restricciones 2 en cada junta de revolución A y D 1 en cada junta revolución-traslación B y C 3 del elemento tierra restricciones totales = 2x2 + 2x1 + 3 = 9 GDL del mecanismo = 12-9 = 3 GDL Si hubiésemos considerado las correderas como sólidos y cada una de las juntas B y C como suma de una junta de revolución más una de traslación, tendríamos: Nº de elementos del mecanismo 5 móviles + tierra = 6 GDL si no hubiese restricciones = 6 * 3 = 18 Restricciones 2 en cada junta de revolución A , B, C y D 2 en cada junta de traslación B y C 3 del elemento tierra restricciones totales = 2x4 + 2x2 + 3 = 15 GDL del mecanismo = 18-15 = 3 GDL . El resultado evidentemente es el mismo. P2. Debemos añadir tantas ecuaciones de excitación como GDL tiene el mecanismo, es decir 3 ecuaciones de excitación. P3. Se pueden proponer las expresiones que se deseen para estas ecuaciones de excitación, algunos ejemplos son: ECSA: f ’1 = k1 f ’2 = k2 f ’3 = k3 Donde evidentemente las aceleraciones angulares son nulas f ”1 = f ”2 = f ”3 = 0 y las posiciones angulares que formulan correctamente las ecuaciones de excitación son: f 1 = k1t + f 10 f 2 = k2t + f 20 f 3 = k3t + f 30 17 w1 = 0 w3 = 0 B D w3 = k3 C w2 = k2 B w2 = 0 C w1= 0 w3 = 0 B w2 = 0 w1 = k1 A Los valores de ki no podrían ser nulos para los tres elementos porque se impediría el movimiento, pero si podrían ser nulos en dos de ellos con lo cual los mecanismos equivalentes en cada caso serían: Se observa como en este caso, para valores nulos de k, las ecuaciones de excitación se convierten en ecuaciones de restricción. Las ecuaciones de restricción son un caso particular por lo tanto de las de excitación. También podríamos haber propuesto ecuaciones de excitación en desplazamientos a algún punto P cualquiera del elemento2 por ejemplo. ECSB: f ’1 = k1 x’P = k5 y’P = k6 Donde evidentemente la aceleración angular f ”1 = 0 y el punto P resulta ser el polo de aceleraciones del elemento 2 aunque no sea su centro instantáneo de rotación: x”P = y”P = 0 Los desplazamientos y giros que formulan de manera formal las ecuaciones de excitación son 18 en este caso: f 1 = k1t + f 10 xp = k5t + xp0 yp = k6t + yp0 En el caso particular de que k5 = k6 = 0 , el punto P resultaría ser centro instantáneo de rotación y polo de aceleraciones, las ecuaciones serían entonces de restricción y el mecanismo equivalente sería: D P w1 = k1 B VPx = VPy = 0 A C Como sería muy largo resolver todos los mecanismos propuestos, resolveremos solamente el caso general más complicado f ’1 = k1 f ’2 = k2 f ’3 = k3 Es decir el problema propuesto es: D w3 = k3 w1 = k1 B w2 = k2 C A 19 Cálculo de velocidades: VB’ D w3 = k3 VC’ w1 = k1 B w2 = k2 C A ’ BB VB’ VC’ de V n ió ecc Dir VB VBC Dirección de VCC’ B y C pertenecen al elemento 2; B’ pertenece al elemento 1; C’ pertenece al elemento 3 Analizando el movimiento relativo en la junta C tenemos: VC = VC’ + VCC’ donde la dirección de VCC’ es la BC. Por otro lado como BC es un sólido indeformable se cumplirá: VB = VC + VBC Donde VBC tiene módulo conocido = w2. BC La dirección de VBC es perpendicular a BC y su sentido es descendente congruente con w2. Sustituyendo tenemos: VB = VC + VBC = VC’ + VCC’ + VBC Por otro lado analizando el movimiento relativo en la junta B tendremos: 20 VB = VB’ + VBB’ donde la dirección de VBB’ es la AB. Como conocemos el valor de V B’ resolvemos gráficamente estas dos últimas ecuaciones vectoriales obteniendo el cinema mostrado en la figura anterior . Los valores de los módulos son supuestos. Cálculo de aceleraciones: D aC’ A B acor C C . V C’C w2 a B’ a CC’ . aC’ aBB’ a cor B Q V BB’ a B’ a cor B acor C aCBn Sabemos que las tres aceleraciones angulares son nulas por definición en las ecuaciones de excitación. Por lo tanto las aceleraciones de C’ y B’ son conocidas, sus módulos serán: |a C’ | = w32 . C’D |a B’ | = w12 . AB’ Las direcciones y sentidos son los mostrados en la figura anterior. Analizando el movimiento relativo en la junta C tendremos. 21 a C’ = aC + aC’C + acor C La aceleración de Coriolis acor C se puede calcular según se muestra en el cinema de aceleraciones a partir de V C’C y de w2 . El módulo de acor C será: |acor C| = 2 |V C’C| . |w2| De la misma forma, analizando el movimiento relativo en la junta B tendremos: a B = aB’ + a BB’ + acorB La aceleración de Coriolis acor B se puede calcular según se muestra en el cinema de aceleraciones a partir de VBB’ y de w1 . El módulo de acor B será: |acorB | = 2 |V BB’| . |w1| Como B y C pertenecen al msmo sólido rígido, podemos expresar aC en función de aB aC = aB + aBCn + aBCt = aB + aBCn por lo tanto: a C’ = aC + aC’C + acor C = aB + aBCn + acor C + aC’C = aB’ + a BB’ + acorB + aBCn + acor C + aC’C en la ecuación anterior, los términos en negrita son conocidos. La resolución gráfica de la misma se muestra en el cinema de aceleraciones de la figura anterior. Evidentemente, los demás casos planteados que el alumno podría haber propuesto, tienen resoluciones más sencillas que este. 22



