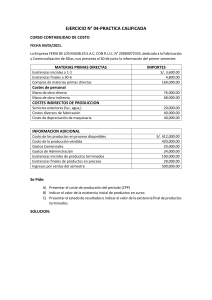
SOLUCIÓN: a) Se obtiene para crecimiento cero –para la raíz no
Anuncio

SOLUCIÓN: a) Se obtiene para crecimiento cero –para la raíz no nula de la función de crecimiento-, esto es para x=800. Entonces, la función crecimiento vegetativo se puede escribir también: 2 2 ⎛ ⎞ ⎛ ⎞ dx x x ⎜ ⎟ ⎜ ⎟ donde ‘r’ es el límite del crecimiento para población =r x− = 0,8 x − ⎜ ⎜ 800 ⎟ dt K ⎟ ⎝ ⎝ ⎠ ⎠ nula. K X = c) El volumen de existencias para máxima producción sostenible es K/2=400. La máxima producción sostenible es el crecimiento vegetativo de ese volumen de Kr = 160 existencias: H = 4 d) − rt 1+ e es decir X = 800 b) − 0 ,8 t 1+ e ⎛ X2 Vendrá dado por la ecuación: H = r ⎜⎜ X − K ⎝ ⎞ ⎛ X2 ⎞ ⎟⎟ , esto es, 100 = 0,8⎜⎜ X − ⎟ 800 ⎟⎠ ⎠ ⎝ Hay dos soluciones, simétricas respecto a X=K/2. La de la derecha es la de equilibrio, ya que el mantenimiento del nivel de extracción H=100 tiende a disminuir las desviaciones del nivel de existencias. e) El nivel de esfuerzo, E, debe ser el que resulta en la extracción máxima sostenible, H=160, calculada anteriormente, que se obtiene en nivel de existencias X=400. Entonces E=H/X=2/5. Para la función de producción H=EX se puede obtener también como la mitad del esfuerzo máximo, que es igual a ‘r’. f) El nivel de esfuerzo sostenible en función de la población es: X⎞ ⎛ ⎛ E⎞ E = H / X = r ⎜1 − ⎟ , de donde, X = K ⎜1 − ⎟ , por lo que el nivel de extracción K⎠ r⎠ ⎝ ⎝ ⎛ E2 ⎞ ⎟. sostenible en función del esfuerzo es H = K ⎜⎜ E − r ⎟⎠ ⎝ Si el precio es ‘p’ y el coste de la unidad de esfuerzo es ‘w’, los beneficios y costes serán: ⎛ E2 ⎞ ⎟; B = pK ⎜⎜ E − r ⎟⎠ ⎝ C=wE El óptimo de propiedad individual se obtendrá cuando se igualen costes y beneficios marginales, esto es: r wr 1 ⎛ 2E ⎞ pK ⎜1 − = 0,4 − = 0,35 . ⎟ = w , es decir: E = − 2 2 pK r ⎠ 20 ⎝ ⎛ E⎞ La población correspondiente a ese esfuerzo sostenible es X = K ⎜1 − ⎟ = 450 . r⎠ ⎝ Vemos que el esfuerzo es algo menor que el de máxima producción sostenible y la población algo mayor. g) Para libre acceso B=C, esto es, pH=wE=w(H/X) Luego X=w/p=100. El esfuerzo será X⎞ ⎛ E = r ⎜1 − ⎟ = 0,7 ⎝ K⎠ h) Debe cumplirse que para el esfuerzo de máxima producción sostenible: r/2, los costes, wE, coincidan con los beneficios, pKr/4. Es decir: wr pKr w K = ⇔ = = 400 2 4 p 2 En nuestro caso, fijo w en 100000, el precio debería situarse en 250 en lugar de en 1000. i) Cuando la pendiente de H(E) a la curva de costes sea horizontal. Es decir, w=0. j) Cuando w=derivada de BT(E) en el origen, es decir, w w = pK ⇔ = 800 ⇔ E = 0 p k) El primero de los resultados es factible y muestra que el libre acceso no implica necesariamente la esquilmación del recurso, sin embargo esa situación podría estar alejada del óptimo económico. Por el segundo vemos que es inverosímil que el óptimo económico coincida con la máxima producción sostenible. Además el nivel de existencias será mayor que el de máxima producción sostenible. El óptimo económico supone, pues, un avance en la dirección de una mayor conservación de los recursos. El tercer supuesto significaría en realidad máxima conservación, sólo se produciría con un nivel de coste del esfuerzo muy elevados con relación al precio. l) La producción sostenible vendría expresada en función del esfuerzo ⎛ 3E 2 ⎞ ⎟ y a partir de aquí se obtienen resultados ligeramente así: H = K ⎜⎜ E − r ⎟⎠ ⎝ diferentes. IT y CT para distintos niveles de esfuerzo Kr/6 Emáx=r/3