Documento PDF de referencia

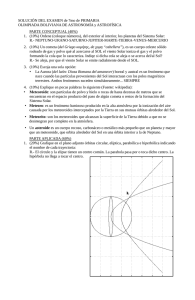
 ACTIVIDAD 8.Cálculo distancia Tierra-Sol a partir de imágenes tránsito de Venus.
Por
Sr. Miguel Ángel Pío Jiménez. Astrónomo Instituto de Astrofísica de Canarias, Tenerife.
Sr. Juan Carlos Casado. Astrofotógrafo tierrayestrellas.com, Barcelona.
Dr. Miquel Serra-Ricart. Astrónomo Instituto de Astrofísica de Canarias, Tenerife.
Dr. Lorrain Halon. Astrónomo University College Dublin, Irlanda.
Dr. Luciano Nicastro. Astrónomo Istituto Nazionale di Astrofisica, IASF Boloña.
1 - Objetivos de la actividad
Mediante esta actividad aprenderemos a calcular la distancia Tierra-Sol (Unidad
Astronómica) a partir de imágenes digitales utilizando el método de la paralaje solar durante el
tránsito de Venus.
Los objetivos que se pretenden alcanzar son los siguientes:
- Aplicar una metodología para el cálculo de un parámetro físico (Unidad
Astronómica o distancia media Tierra-Sol) a partir de un observable (imágenes
digitales).
- Aplicar conocimientos de Matemáticas y Física (Trigonometría, Álgebra y
Cinemática) así como de Astronomía (Leyes de Kepler).
- Conocer y aplicar técnicas de análisis básico de imágenes (escala angular,
medición de distancias,…).
- Trabajar cooperativamente en equipo, valorando las aportaciones individuales y
manifestando actitudes democráticas.
2 – Instrumentación.
La práctica o actividad se realizará a partir de imágenes digitales obtenidas durante el
tránsito de Venus en junio del año 2012 (ver sky-live.tv). Por favor, véase el Glosario de entrega
con este documento para una referencia rápida de los términos utilizados, abreviaturas y
unidades físicas.
3 – Fenómeno.
3.1.- Ocultaciones y tránsitos
Una ocultación es la alineación o interposición de un cuerpo celeste por otro visto desde
la Tierra. Un tránsito es un fenómeno de ocultación en el que el cuerpo que produce la
ocultación es mucho más pequeño que el ocultado. En tal caso no se produce la desaparición del
cuerpo más distante, sino un paso o tránsito del primero proyectado sobre la superficie del
mayor.
Desde nuestro planeta se pueden observar los tránsitos de los planetas interiores,
Mercurio y Venus sobre el disco solar. Mercurio se mueve en un plano que forma 7º con la
Tránsito de Venus 1 eclíptica, de manera que la mayor parte de las veces Mercurio pasa «por encima» o «por
debajo» del disco solar, sin que se produzca el tránsito. Mercurio suele transitar en promedio
unas 13 veces por siglo en intervalos de 3, 7, 10 y 13 años. El último tránsito de Mercurio
aconteció el 8 noviembre de 2006.
3.2.- Tránsitos de Venus
La explicación de los tránsitos de Venus es análoga a los de Mercurio. Al igual que en el
caso de Mercurio, la órbita de Venus también se encuentra inclinada respecto a la de la Tierra
( 3,4 º). Si no fuera así, habría un tránsito de Venus cada 584 días (su periodo sinódico, que es el
tiempo que tarda Venus en volver a la misma posición con respecto al Sol, visto desde la Tierra).
La Tierra atraviesa cada año la línea de los nodos de la órbita de Venus (ver Figura 1) en
torno al 6-7 de junio y al 9-10 de diciembre. Si para esas fechas coincide con una conjunción
inferior, se producirá un tránsito.
Figura 1 : Una ilustración de la línea de Nodos de la órbita de Venus, cuando se intersecta con la de la
Tierra.
En realidad, los tránsitos de Venus son unos fenómenos extraordinariamente inusuales, ya
que en promedio hay dos cada poco más de un siglo. Estos dos tránsitos están separados 8 años
y el intervalo entre parejas de tránsitos va alternándose entre los 105,5 y los 121,5 años. En
algunas ocasiones, como sucedió en 1388, uno de los tránsitos de la pareja puede no producirse,
ya que no coincide con el paso por el nodo. La última pareja de tránsitos de Venus sucedió el 9
de diciembre de 1874 y el 6 de diciembre de 1882.
El último tránsito, visible desde Europa, tuvo lugar el 8 de junio de 2004 (figura 1), y el
próximo acontecerá el 6 de junio de 2012.
Tránsito de Venus 2 Figura 2: Tránsito de Venus del 8 de junio de 2004 mostrando su recorrido
sobre el disco solar (a intervalos de 45 minutos). Imagen Juan Carlos Casado
© tierrayestrelllas.com
Desde el punto de vista visual, el fenómeno del tránsito de Venus es similar al de
Mercurio: Venus se proyecta como un círculo negro desplazándose lentamente sobre el brillante
disco solar. Los tránsitos de Venus duran como máximo algo más de 8 horas. Durante el tránsito
Venus presenta un diámetro aparente de 61", por lo que resulta perfectamente visible a simple
vista con los medios de protección adecuados para la observación solar (filtros adecuados).
Además, se produce el denominado efecto de la gota negra cerca de los bordes del disco solar.
-Efecto de la “gota negra”. Justo después del contacto interno entre los discos del Sol y
Venus, el disco del planeta parece quedarse unido durante algunos segundos al extremo del
disco solar, deformándose para adoptar la apariencia de una gota negra (Figura 3). Este
fenómeno se vuelve a repetir justo antes del último contacto interno. El efecto de la gota negra
impide cronometrar con precisión los instantes de contacto entre el disco del planeta y el del
Sol1, y ha sido la causa principal por la que las observaciones llevadas a cabo para determinar la
distancia entre el Sol y la Tierra presentaran una cierta indeterminación. A pesar de que este
efecto se atribuyó a la atmósfera de Venus usando imágenes del tránsito de Mercurio del satélite
TRACE (Transition Region and Coronal Explorer, NASA, USA), se encontró 2 que las
principales causas del efecto de la gota negra son la distorsión de las imágenes (debido a la
turbulencia atmosférica y la difracción del telescopio) y el oscurecimiento del limbo solar. Esto
implica que el desarrollo del efecto de la gota negra, visto por un observador desde la Tierra
depende principalmente de las condiciones atmosféricas y la calidad de su instrumento (tamaño
y óptica del telescopio usado).
1
2
Indicaciones para aumentar la precisión en los contactos: http://www.transitofvenus.nl/blackdrop.html
Véase el estudio científico http://nicmosis.as.arizona.edu:8000/POSTERS/TOM1999.jpg Tránsito de Venus 3 Figura 3: Proceso de formación del fenómeno de la gota negra en el momento de la entrada de Venus en el
disco solar. Créditos: Juan Carlos Casado.
-Efecto de la “Aureola de Venus”. Durante los tránsitos de Venus se ha observado un
arco luminoso, de alrededor de 0,1 segundo de arco de ancho, alrededor de la circunferencia del
disco de Venus, que se encuentra parcialmente fuera del limbo solar. Fue descrita por primera
vez por el científico ruso Mikhail Lomonosov en la observación del tránsito de Venus en 1761.
Justo después de la salida del contacto interior, este efecto aureola se inicia con la aparición de
un punto de luz brillante cerca de uno de los polos de Venus. Por lo general, este punto poco a
poco se convierte en un fino arco conforme Venus se aleja del sol (ver Figura 4). En la entrada
el proceso se producirá en orden inverso. El brillo de la aureola es similar a la de la fotosfera
solar por lo que es conveniente el uso de un filtro solar. Sin embargo, sólo puede ser visto en
buenas condiciones de observación, utilizando un buen telescopio.
El efecto aureola se debe a la refracción de la luz del sol en la densa atmósfera de Venus. Las
condiciones atmosféricas de Venus que determinarán la aparición de la aureola. Si el índice de
refracción de su atmósfera es pequeño, la aureola que se romperá en puntos brillantes. Pero si el
índice de refracción de la atmósfera es alto, la aureola se extenderá por todo limbo del planeta
como un arco completo (ver Figura 4).
Figura 4: Efecto de la Aureola de Venus detectado en el tránsito de Venus 2004 con el Telescopio Solar Sueco de 1m
ubicado en Roque de los Muchachos (La Palma , Instituto de Astrofísica de Canarias). Credit: D. Kiselman, et al.
(Inst. for Solar Physics), Royal Swedish Academy of Sciences.
Tránsito de Venus 4 3.3.- Los tránsitos anteriores
Siglo XVII. El primer tránsito observado de Venus tuvo lugar el 4 de diciembre de 1639.
Horrocks, un clérigo de Liverpool (Inglaterra) que había estudiado Astronomía y Matemáticas,
pudo seguir el tránsito del planeta cuando éste ya había comenzado.
Siglo XVIII. A principios del siglo XVIII, el astrónomo inglés Edmund Halley propuso
aprovechar los tránsitos de Venus para determinar con gran precisión la paralaje solar, lo que
permitiría ajustar el tamaño del sistema solar conocido. La paralaje solar es el ángulo que desde
el Sol subtiende el radio ecuatorial de la Tierra (Figura 5), y es a partir de él, como
determinaremos, más adelante, la distancia Sol-Tierra.
Figura 5: Representación esquemática para mostrar la paralaje solar o ángulo ρ. Este ángulo
en realidad es muy pequeño, pero a efectos de claridad se ha exagerado su valor.
Aprovechando el tránsito de Venus que se iba a producir en 1761, astrónomos de todo el
mundo, comisionados por sus gobiernos se prepararon para la observación. En total, el tránsito
fue observado desde unos 70 lugares distribuidos alrededor del globo terrestre, constituyendo la
primera gran empresa científica internacional. Sin embargo, los resultados obtenidos no
estuvieron a la altura de las expectativas. El mal tiempo en muchos de los lugares de
observación, la dificultad de determinar con precisión la localización geográfica del lugar en
que la observación se realizaba y el efecto de la gota negra dificultaron la aplicación del método
de Halley (ver apartado 4).
En la observación del tránsito de 1769 hubo 150 observadores oficiales y otros muchos
aficionados. Entre los observadores se encontraba el célebre capitán James Cook, que realizaba
el primero de sus viajes.
Siglo XIX. Los tránsitos de 1874 y 1882 fueron también seguidos por cientos de
observadores enviados por las academias científicas de multitud de países. El Boletín de la
Sociedad Astronómica de Londres recoge que se obtuvieron 3.440 pruebas fotográficas de los
distintos aspectos que ofreció el fenómeno.
En el tránsito de 1882, España participó por primera vez de forma oficial, enviando dos
grupos de observadores, uno a Cuba y otro a Puerto Rico.
En cualquier caso, el fenómeno de la gota negra volvió a perjudicar las observaciones,
por lo que la paralaje solar quedaba determinada entre un valor de 8,790" y 8,880", lo que
corresponde a una distancia Sol-Tierra de entre 148,1 y 149,7 millones de km.
Tránsito de Venus 5 Tránsito de 2004. Actualmente el método de la paralaje es obsoleto, y las actuales
mediciones efectuadas con sondas espaciales y técnicas de radar cifran la paralaje en un valor de
8,79415" ó 149,59787 millones de km. Durante el tránsito de 2004 se realizaron observaciones
y fotografías por todo el mundo, creándose para la ocasión una red educativa internacional para
determinar la Unidad Astronómica como experimento académico y conmemorativo.
3.4.- El tránsito de Venus de 2012
El tránsito del 5 de junio de 2012 resultará visible totalmente desde el norte de los países
nórdicos, extremo Oriente, Rusia oriental, Mongolia, el este de China, Japón, Filipinas, Papúa
Nueva Guinea, centro y este de Australia, Nueva Zelanda, oeste del Océano Pacífico, Alaska,
norte de Canadá y casi toda Groenlandia. Desde Europa sólo será visible al final del tránsito,
cuando amanezca (Figura 6). Después de este tránsito, habrá que aguardar hasta los años 2117
y 2125 para ver nuevos tránsitos de Venus, esta vez en diciembre.
Figura 6: Mapa mundial de visibilidad del tránsito de Venus del año 2012 (créditos F.
Espenak, NASA/GSFC).
4 – Metodología
4.1.- Métodos para calcular la paralaje solar durante un tránsito de Venus
Existen tres métodos principales para calcular la paralaje solar a partir de observaciones
combinadas en dos lugares separados durante el tránsito de Venus.
Un principio fundamental a tener en cuenta sea el método que se utilice, es que la
obtención de resultados será más precisa cuanto más distantes en latitud se encuentren los dos
observadores (por ejemplo, un observador en el hemisferio norte y el otro en el hemisferio sur).
I. El método de Halley.
Consiste en observar y comparar la duración total del fenómeno. Para ello se han de
cronometrar los instantes de los contactos externos o internos del disco de Venus con el disco
solar. Como debe realizarse desde dos lugares en la Tierra donde se pueda observar por
completo el tránsito, pueden existir dificultades meteorológicas que impidan la observación (ver
Figura 7).
Tránsito de Venus 6 Figura 7 : Un diagrama del significado de “Contacto Interior” y “Contacto Exterior”.
II. El método de Delisle.
Consiste en observar y comparar el mismo contacto entre el disco de Venus y el disco
solar. Los contactos externos son a menudo difíciles de determinar por lo que se suelen utilizar
los internos. Tiene la ventaja sobre el método de Halley que amplía la zona de observación útil a
lugares donde sólo uno de los contactos resulta visible.
III. Medición directa de la paralaje diferencial de Venus mediante imágenes.
Para este método son necesarias observaciones simultáneas desde dos localizaciones
geográficas diferentes. El observable que se mide es la distancia entre los centros de las sombras
de Venus sobre el disco del Sol vistos desde los dos lugares. No se pretende describir el cálculo
rigurosamente en éste apartado, pero si se desea conocer mejor, se puede encontrar una
descripción del mismo en el Anexo I.
Figura 8 : Observación del tránsito de Venus por delante del disco del Sol desde dos localidades
M1 y M2 diferentes en un mismo instante de tiempo.
Suponemos la geometría del problema definida en la Figura 8. El punto O es el centro de
la Tierra, C el centro del Sol y V1 y V2 los centros observados de la proyección de Venus visto
Tránsito de Venus 7 desde M1 y M2, respectivamente. Los ángulos D1 y D2 serán las separaciones angulares entre los
centros de Venus y el Sol vistas desde M1 y M2, respectivamente, es decir, los ángulos de
paralaje CM1V1 y CM2V2. Análogamente, podemos definir los ángulos πs y πv como las
separaciones angulares entre M1 y M2 vistas desde el Sol y desde Venus, respectivamente, es
decir, los ángulos M1CM2 y M1VM2. Por definición tenemos,
sen !! =
!
;
!!
sen !! =
!
!!"
donde rT es la distancia Tierra-Sol, rVT es la distancia Venus-Tierra y d es la distancia
entre M1 y M2 en línea recta y en el Anexo II se describe como obtenerla.
Vamos a tomar en cuenta las siguientes aproximaciones:
•
•
•
•
Como la distancia entre los objetos es muy grande, y el paralaje es muy pequeño,
podemos aproximar el valro del seno del paralaje por el del propio ángulo de
paralaje, o lo que es lo mismo sen πi ≈ πi
Supondremos que la Tierra, Venus y el Sol están alineados, de manera que rvT =
rT-rv, donde rv es la distancia Venus-Sol.
Los puntos de observación M1 y M2 están en el mismo meridiano, es decir, M1 ,
M2 , C y V en el mismo plano (son coplanarios).
También asumiremos que éstos puntos son coplanarios durante todo el tránsito,
aunque en realidad esto no es cierto ya que la Tierra rota durante el transcurso del
mismo y la geometría del sistema cambia.
Entonces se cumplirá que la distancia entre las sombras de Venus en la superficie del Sol
Δπ = πv – πs y tendremos,
!! =
!
!!
and π! = !
!! !!!
y de aquí se deduce que:
π! · r !
!! − !!
π! = !" = !!
!!
− 1 = !!
!! − !!
!!
!! − !!
y por tanto,
!! = !"
!!
!
− 1 =
!!
!!
que despejando nos queda que la distancia Tierra-Sol en el momento de la observación es,
!! = !" (!
!
! /!! ! !)
Ecuación [1]
donde Δπ es la cantidad observable (distancia entre los centros de las sombras de Venus
en la superficie solar y debe expresarse en radianes), d se determina a partir de las
!
localizaciones (ver Anexo II), y el cociente ! entre las distancias Tierra-Sol y Venus-Sol
!!
podemos deducirlo a partir de las efemérides (ver Anexo III). Si expresamos d en kilómetros la
unidad de distancia Tierra-Sol será también en kilómetros.
Tránsito de Venus 8 El observable Δπ puede calcularse de dos formas que se describen a continuación.
4.2.- Método 1. Método de “Las Sombras”.
Este método consistirá en fotografiar el tránsito desde dos lugares distintos exactamente
en el mismo instante, con el mismo tipo de instrumento, de manera que al superponer las dos
imágenes se puede medir la distancia angular entre los centros de la sombra de Venus
(parámetro Δπ). Los detalles del procedimiento a seguir se encuentran en el apartado 5.2.1.
4.3.- Método 2. Método de “Las Cuerdas”.
En este caso tendremos en cuenta toda la trayectoria que la sombra de Venus traza sobre
la superficie del Sol (ver figura 1), llamando a la línea que une las posiciones del centro de ésta,
cuerda M1 o cuerda M2, en función del punto de observación terrestre.
Debido a que la distancia Tierra-Sol varía muy poco en el transcurso del tránsito (la
variación es de solo 7.500Km frente a los 150 Millones de Km que es la distancia media TierraSol) entonces podemos suponer que las dos cuerdas son paralelas y ahora el observable a medir
no es la distancia entre las sombras instantáneas de Venus sino la distancia entre las dos cuerdas
que se forman en la superficie del Sol durante el tránsito (ver Figura 9).
Usando el Teorema de Pitágoras, nosotros podemos escribir las siguientes expresiones:
Figura 9 : Una representación de las dos trayectorias
“cuerdas”, que se producen sobre la superficie solar, con
los nombres de los puntos que se utilizarán en la
explicación matemática. Créditos M. A. Pío (IAC)
Haciendo uso del teorema de Pitágoras, podemos escribir las siguientes relaciones:
! ! ! = ! !
!
−
!! !! !
!
! !
!! ! = !
−
!! !! !
!
donde D es el diámetro solar. De modo que A'B' se puede expresar de la siguiente forma:
!
!
!
!
!! =! !−!! =
!
2
!
!! !!
−
2
!
− !
2
!
!! !!
−
2
!
Con lo que, midiendo las líneas A1A2, B1B2 y el diámetro solar D, obtendremos entonces
el paralaje Δπ según:
Tránsito de Venus 9 Δπ =
1
2
! ! − !! !!
!
− ! ! − !! !!
!
5 – Cálculos para el Tránsito de Venus del 5/6 de Junio del 2012.
5.1 – Pongámonos en situación.
En éste apartado se pretende ya, por último, hablar específicamente del próximo tránsito
de Venus, intentando acercarnos lo más posible a la situación que nos encontraremos en junio
cuando nos veamos delante del ordenador, observando el tránsito e intentando, con las imágenes
que se tomarán para ello, calcular la distancia Tierra-Sol. Para ello vamos a empezar haciendo
una pequeña descripción de la instrumentación que se utilizará para realizar la práctica, así
como de los valores de latitud y longitud (aproximados porque puede que cambien ligeramente
en la observación final) de los lugares desde donde se tomarán dichas imágenes, y de todos
aquellos comentarios y descripciones necesarias para culminar con éxito los cálculos.
5.1.1 – Descripción instrumental y localización de las observaciones.
Como ya se describió anteriormente, para evitar complicaciones en el cálculo, hemos
seleccionado dos lugares en la superficie terrestre donde el tránsito fuera visible en su totalidad
y que tuvieran coordenadas de longitud similares, y éstos han sido:
Cairns (Australia): Latitud : -16º 55’ 24,237”
Longitud: 145º 46’ 25,864”
Sapporo (Japón): Latitud: 43º 3’ 43,545”
Longitud: 141º 21’ 15,755”
Con respecto a las imágenes, se tomarán, en tiempo real, con un telescopio marca
VIXEN, modelo VMC110L, que tiene una relación focal de f/9,4, equivalente a una focal de
1035 mm, con un apertura de 110 mm, colocando un filtro adecuado para la observación solar.
En el foco del telescopio se acoplará una cámara Canon 5D Mark II de 21Mpix.
Con éste Telescopio y ésta cámara, el tamaño de la imagen del sol en el plano de la
cámara será de unos 1630 píxeles.
Dado que el tamaño aparente del Sol en el cielo es de 31,5’ de arco, la escala angular de
la imagen será:
!"#$%$ (!) =
31,5 !"#. !" !"#$ (′) · 60 !"#. !" !"#$ (")
= 1,16 "/!"#
1630 !"#
El Telescopio se montará sobre una montura denominada “Astrotrack”, muy estable y de
fácil montaje, que contiene un sistema sencillo motorizado que permite seguir el movimiento
solar sin complicaciones.
Y con respecto a la frecuencia en la toma de imágenes, éstas se tomarán con un periodo
de 5 minutos durante todo el tiempo que dure el evento, del orden de 5 horas, y tras un
procesado simple, se irán colocando en tiempo real en una dirección ftp, que se dará en el
momento, de modo que se permita el fácil y libre acceso a las mismas. Cada una de las
imágenes tendrá información del tiempo (UT o Tiempo Universal) y lugar en que fue tomada.
Tránsito de Venus 10 Figura 10: Fotografía de la instrumentación que se usará en el Tránsito. Créditos:
M.A. Pío (IAC).
5.2 – Descripción general de la forma de trabajo.
En los apartados 5.2.1 y 5.2.2, explicaremos desde un punto de vista práctico, como
determinar Δπ utilizando los dos métodos descritos anteriormente. Recomendamos que si el
tiempo lo permite, se utilicen ambos métodos para realizar la experiencia y así comparar los
resultados obtenidos.
5.2.1 – Método 1. “Las Sombras”.
Partiremos de dos imágenes tomadas en el mismo instante de tiempo (o lo más cercano
posible), desde cada una de las diferentes localizaciones. Ahora tendremos que determinar la
distancia que hay entre las sombras de Venus.
Para calcular la distancia Δπ deberíamos alinear las dos imágenes (transformación de
rotación y traslación ya que las dos tendrán la misma escala) y realizar la medida de la distancia
entre las sombras de Venus con cualquier software de tratamiento de imágenes. Para simplificar
el proceso hemos realizado unas transformaciones matemáticas para determinar Δπ a partir de
las coordenadas cartesianas de las sombras de Venus, de una mancha en la superficie solar y los
centros del Sol en cada imagen, SIN necesidad de alinear las imágenes. En la figura 7 se
presentan las observaciones (simuladas con un software astronómico) del tránsito (hora 0:45UT
Tránsito de Venus 11 del día 6 de junio de 2012) realizadas desde los dos puntos de observación de Cairns (Australia)
y Sapporo (Japón).
Figura 11: Imágenes realizada con software astronómico, simulando las observaciones del tránsito de Venus a las
0:45UT del día 6 de junio de 2012. Créditos M.A Pío, (IAC).
Siguiendo los cálculos Anexo IV, el cálculo del observable Δπ, se determinará a través de
la expresión:
Δ! =
!
Δ!! ! + Δ!! !
donde las componentes Δπx y Δπy se pueden expresar como:
Δ!! = !! − !!! cos ! + !! − !!! sin ! − !! + !!!
Δ!! = − !! − !!! sin ! + !! − !!! cos ! − !! + !!"
donde (!! , !! ) y (!! , !! ) son las coordenadas de la sombra de Venus en las imágenes de
Sapporo y Cairns, respectivamente, mientras (xc1,yc1), (xc2,yc2) son las coordenadas del centro
del Sol en Sapporo y Cairns, respectivamente, todo referido al sistema de coordenadas S.
En nuestro caso, para el día 6 de Junio del 2012 y observando desde Cairns, y Sapporo,
ese ángulo vale (ver cálculos en Anexo IV):
θ = 108º 4’ 17,92”
Y sustituyendo:
Δ! =
!
Δ!! ! + Δ!! ! = 8,4 !í!"#"$
Después de determinar Δπ, pasaremos a realizar el cálculo matemático que conlleva el
método. Siguiendo el Anexo II, el valor de d será:
d = 6662,9 Km
Tránsito de Venus 12 Hay un valor que también se proporcionará en el momento de las observaciones, que es
necesario para la realización práctica, que es la relación que existe entre el radio vector que une
la Tierra con el Sol y Venus y el Sol (rT/rV).
Δπ debe expresarse en segundos de arco, por lo que habrá que hacer uso del valor de
escala, y después realizar un cambio de unidades de segundos de arco a radianes. Para el caso de
las imágenes realizadas con el software astronómico, a modo de ejemplo, el diámetro del sol, en
píxeles, es de 715 píxeles, por tanto, la escala será :
!"#$%$ (ℇ) =
31,5! [!"#$%&' !" !"#$ (′)] · 60[!"#$%&'! !" !"#$ (")]
= 2,643 "/!í!"#
715 !í!"#!"
Notar que éste es sólo en éste caso, usando los tamaños que aparecen en la figura 11, pues
para el momento de la retransmisión, el valor de la escala será el expresado en el apartado
5.1.1):
Considerando que rT/rV = 1,39759 a las 0:45 UT (valor que se obtiene de las efemérides,
en función del día y de la hora), sustituyendo valores en la ecuación [1] del apartado 4.1.
obtenemos,
!! =
6662,9 !"
!"#. !"# (")
!
8,4 !í!"#"$ · ε
·
648000
!í!"#"$
!"#
(1,39759 − 1)
!"#. !"#.
= !"#, ! · !"! !"
De modo que podremos calcular el valor de rT, la distancia Tierra-Sol. Comentar que el
valor de Δπ en la expresión anterior, debe estar en radianes, por lo que por eso aparece ese
término π/648000, el cual es necesario utilizar para el cambio de unidades (de segundos de arco
a radianes).
5.2.2 - Método 2. “Las Cuerdas”.
Éste método es mucho más sencillo que el anterior ya que sólo hace falta determinar el
valor, sobre las imágenes, de la longitud de las líneas o cuerdas que crea la trayectoria de la
sombra de Venus sobre la superficie del Sol. Evitamos el problema del método de “Las Sombras”
en el que teníamos que tener una sincronización entre los dos lugares de observación, a la hora
de la toma de las imágenes, para poder considerar que ambas han sido tomadas en el mismo
instante. En el método de “Las Cuerdas” en algún momento del tránsito debe estar despejado
“simultáneamente” en ambas localizaciones. Sin embargo, el método de “Las Cuerdas” tiene el
problema de que deberemos esperar a que termine todo el tránsito para poder aplicarlo si bien es
cierto que si las condiciones ambientales son malas en algún momento y hay algún punto que no
se puede tomar, podemos extrapolar la trayectoria con el resto derivando la correspondiente
cuerda. Por contra, hay que tener en cuenta que las imágenes de cada lugar habrá que alinearlas
perfectamente.
Hacer notar que la longitud de las dos cuerdas no será muy diferente sobre la superficie
solar, por lo que hay que tener cuidado con la medida.
Resumiendo, necesitaremos, como ya se explicó anteriormente, el valor del diámetro
solar (D), y la longitud de las líneas M1 y M2, expresadas todas las medidas en las mismas
unidades. La longitud de las líneas M1 y M2, según la imagen, son las que unen A1 y A2 y B1 B2,
respectivamente (ver Figura 9), y se pueden medir, tanto en mm como en píxeles, según si la
medición se hace con regla tras imprimir la imagen, o con un software de representación y
manipulación de imágenes (software propietario, por ejemplo Photoshop o Corel Draw, o
Tránsito de Venus 13 incluso el Paint de Windows, y software libre como el Gimp, o cualquier software que permita
calcular tamaños de objetos dentro de una imagen). Recomendamos realizar las medidas en
píxeles.
Figura 12: Imagen realizada con software astronómico, donde se observa la longitud de
las cuerdas. La imagen del Sol no es real. Créditos M.A Pío, ( IAC )
Para el ejemplo de la imagen (Figura 12), el valor del diámetro del Sol D, en píxeles, es
de 711, la cuerda M1 mide 565 píxeles (B1B2), y la cuerda M2 (A1A2) 578 píxeles.
Nota: Si se quiere medir la longitud de las cuerdas en milímetros, hay que ser
consecuente con las unidades, de manera que hay que recalcular el factor de escala, siguiendo la
expresión de la página 17, indicando el diámetro del Sol en mm. La escala, ε, deberá expresarse
entonces, en [seg. arco/mm].
A partir de aquí, el cálculo es sencillo. Primero necesitamos calcular A’B’, donde A’B’
es, según la Figura 9, la distancia que existe entre las dos cuerdas, distancia que está relacionada
directamente con el valor de Δπ . Así, la expresión que usaremos será:
Δ! = !! ! ! =
1
2
! ! − (!! !! )! − ! ! − !! !!
!
= 8,79 !í!"#"$
Ya por último, sustituyendo en la Ecuación [1] quedará:
!! =
6662,9 !"
= !"#, ! · !"! !"
!"#. !"# (")
!
!"#
8,79 !"# · ε
·
(1,397589 − 1)
!"#
648000 !"#. !"#.
donde, de nuevo, el valor de rT es la distancia Sol-Tierra, d es la distancia entre los
observadores, determinada de acuerdo al Anexo II, ε es el valor de escala descrito, y la razón
rT/rV tiene un valor igual a la media de los valores durante todo el tránsito.
Un factor a tener en cuenta y que no se ha comentado anteriormente es que el valor del
radio vector que une la Tierra con el Sol, y su homólogo que une Venus con el Sol, ambos
varían con el tiempo debido a que las órbitas tanto de la Tierra como de Venus son elípticas. En
el Método 1, al considerar un instante de tiempo fijo (0:45 UT), la relación entre rT/rV es el valor
instantáneo de ese momento, pero para el Método 2, como se considera el tránsito completo, el
valor de la relación rT/rV a utilizar es el valor en el punto medio del tránsito. De todas maneras,
Tránsito de Venus 14 se puede observar que ambos valores difieren en muy poco pues en un periodo tan corto de
tiempo (algo más de 5 horas que dura el tránsito), la variación en la distancia Tierra-Sol es
prácticamente despreciable (ver Anexo III).
6 – Direcciones de Internet
•
•
•
•
•
•
•
•
•
Transmisión del tránsito en directo a través de Internet:
http://www.sky-live.tv
Portal de GLORIA:
http://gloria-project.eu
Predicciones on line del tránsito 2012:
http://www.transitofvenus.nl/details.html
Información general y datos sobre el tránsito:
http://www.transitofvenus.org
Métodos seguros para la observación solar:
http://www.transitofvenus.org/june2012/eye-safety
Datos y predicciones:
http://eclipse.gsfc.nasa.gov/transit/venus0412.html
Expediciones científicas del grupo Shelios para observar fenómenos astronómicos:
http://www.shelios.com
Descripción del cálculo expuesto para la paralaje solar con ejemplos:
http://serviastro.am.ub.es/Twiki/bin/view/ServiAstro/CalculTerrasolapartirDeVenus
y
http://www.imcce.fr/vt2004/en/fiches/fiche_n05_08_eng.html
Descripción de las Leyes de Kepler:
http://infobservador.blogspot.com/2010/11/las-leyes-de-kepler.html
y
http://www.portalplanetasedna.com.ar/leyes_kepler.htm
Tránsito de Venus 15 ANEXO I: Medición directa de la paralaje diferencial de Venus
mediante imágenes. Cálculos detallados.
La determinación de la distancia Tierra-Sol se basa en el efecto de paralaje (como se ha
visto anteriormente) por el cual, desde dos localizaciones diferentes, Venus se proyecta en
lugares distintos sobre el disco solar. El efecto de perspectiva será tanto más importante cuanto
más separados están los dos lugares de observación y en consecuencia se obtendrá una distancia
más precisa. La manera más sencilla es tomar fotografías en el mismo instante desde los dos
lugares con un instrumental semejante.
Las observaciones se han de complementar con las leyes de Kepler que describen las
órbitas de los planetas alrededor del Sol, que Johannes Kepler (1571-1630) dedujo a partir de
numerosas observaciones del movimiento de los planetas. La ley de la gravitación universal,
formulada por Isaac Newton (1642-1727), aplicada al caso de dos cuerpos en movimiento en
torno a un centro de masas común explica las tres leyes empíricas de Kepler. (ver Anexo IV)
Desde dos localidades diferentes M1 y M2 (ver figura 13) y en el mismo instante de
tiempo t, Venus se proyecta en dos posiciones diferentes V1 y V2 sobre el disco solar por efecto
de la paralaje.
Figura 13 : Observación del tránsito de Venus por delante del sol desde dos localidades diferentes, M1 y
M2 en el mismo instante de tiempo.
El punto O es el centro de la Tierra, C el centro del Sol y V1 y V2 los centros observados
de la proyección de Venus visto desde M1 y M2, respectivamente. Los ángulos D1 y D2 serán las
separaciones angulares entre los centros de Venus y el Sol vistas desde M1 y M2,
respectivamente, es decir, los ángulos de paralaje CM1V1 y CM2V2. Análogamente, podemos
definir los ángulos πs y πv como las separaciones angulares entre M1 y M2 vistas desde el Sol y
desde Venus, respectivamente, es decir, los ángulos M1CM2 y M1VM2. Dado que los cuatro puntos M1, M2, C y V no están en el mismo plano (el caso más
común será no tener las dos localizaciones M1 y M2 sobre el mismo meridiano, ni la Tierra,
Venus y el Sol perfectamente alineados), la geometría del problema se complica un poco. En la
Figura 14, se puede ver como la distancia Δπ entre los dos centros de Venus es precisamente la
única cantidad observable, correspondiente a Δπ = πv – πs , que permite calcular la distancia al
Sol.
La realización práctica de la medida de Δπ a partir de las dos fotografías se puede hacer
midiendo la posición del centro de Venus en cada fotografía en relación a un punto de referencia
en el disco solar (una mancha, por ejemplo) y compararlo con el tamaño de este disco. Las
medidas sobre las fotografías se realizan en unidades de longitud, en mm por ejemplo, que
Tránsito de Venus 16 deberán transformarse a medidas angulares que se puede obtener conociendo el diámetro
aparente del Sol y la escala (unidad de longitud/segundos de arco) de las imágenes.
Sean (x1,y1) y (x2,y2) las separaciones en mm entre el centro del disco de Venus y la
mancha de referencia en las direcciones horizontal y vertical para cada una de las fotografías.
Las separaciones en segundos de arco se obtienen multiplicando cada una de las cantidades x1 e
y1, que se obtienen en píxeles o en mm., por el factor de escala (ε)
!"#$%$ (ℇ) =
!"á!"#$% !"#$% !"#$%&'% (" !" !"#$)
!"á!"#$% !"# !"# (!! ! !í!"#"$)
La distancia entre los centros de Venus en las dos fotografías será:
Δπ(segundos de arco) = [ (x2 – x1)2+ (y2 – y1)2 ]1/2 · ε
Si las dos fotografías se toman con dos telescopios que proporcionan la misma escala, que
es nuestro caso, se puede tomar como punto de referencia el centro del disco solar C.
Figura 14 : Posiciones de las proyecciones de Venus
sobre el disco del Sol.
Supongamos que rV y rT son las distancias entre el centro del Sol y los de Venus y la
Tierra, respectivamente, en el momento t de la observación. Puesto que la proyección d de la
distancia entre M1 y M2 en el plano perpendicular a OC es pequeña en comparación a las
distancias Tierra-Sol y Tierra-Venus, podemos aproximar:
πs = d/rT
πv = d/(rT -rV)
y de aquí se deduce que:
πv = πs rT/(rT -rV)
Δπ = πs (rT/(rT -rV)-1) = πs rv/(rT -rV)
y por tanto,
πs = d/rT = Δπ (rT/rV - 1)
Tránsito de Venus 17 Esta última fórmula expresa que conocida la distancia angular Δπ entre los dos centros V1
y V2, y la relación rT/rV entre las distancias Tierra-Sol y Venus-Sol, se puede deducir la paralaje
πs y que, conocida la distancia proyectada d entre las dos localizaciones (ver Anexo II), se puede
deducir la distancia rT. (En todas estas expresiones los valores de πv, πs y Δπ vienen dados en
radianes. Para convertirlos a segundos de arco y hacerlos compatibles con los cálculos, sólo se
necesita multiplicar por 64800 y dividir por el número π).
Δπ es la cantidad observable, d se determina a partir de las localizaciones (ver Anexo II),
por lo que la única cantidad que falta para resolver el problema es la relación rT/rV entre las
distancias Tierra-Sol y Venus-Sol (ver Anexo III)
Hasta aquí hemos determinado πs y rT , que son la paralaje y la distancia Tierra-Sol en el
instante t de observación.
Determinación de la distancia media
Por otro lado, también podemos determinar la distancia media Tierra-Sol (RT) y la media
correspondiente de paralaje πo, que se relacionan a través del radio ecuatorial de terrestre R, por:
πo ≈ R/RT
y para hacerlo, es necesario hacer alguna consideración adicional.
El término de la distancia media de la Tierra - Sol, que hemos llamado RT, también se
puede definir como el radio que tendría la órbita de la Tierra si se ésta fuera circular y tuviera el
centro en el centro de la elipse que define el órbita real de la Tierra. De esta manera, el valor del
semieje mayor de la órbita real, a, coincide con el valor de RT (a = 1.000014 RT), por lo que se
puede expresar el valor de la paralaje medio como:
!! =
!
! ! !!
! !
! !!
=
· = !!
· ⟹ !! = · · !!
!! ! ! ! !!
! !!
! !
donde rT/a es la relación entre la distancia Tierra-Sol instantánea, rT, y el semieje mayor
de la órbita del Sol, a.
Por lo que partiendo de la relación que teníamos, donde decíamos que πo ≈ R/RT, se
puede despejar el valor de RT que sería el valor de la distancia Tierra-Sol media.
Tránsito de Venus 18 ANEXO II: Determinemos el valor de d.
Si se expresa la proyección d de la distancia entre M1 y M2 en el plano normal a la
dirección Tierra-Sol en unidades del radio ecuatorial terrestre, y la distancia Tierra-Sol en
unidades de la distancia media, tendremos:
πs = [(d/R) / (rT /RT)] (R/RT) ≈ [(d/R) / (rT /RT)] πo
El cociente rT /RT se puede deducir de la primera ley de Kepler como:
rT/RT = 1 - eT cos ET(t)
y por tanto, sólo nos falta calcular d/R (ver Figura 8).
Figura 15 : Proyección de la distancia entre M 1 y M2 en el plano normal a la dirección SolTierra.
Haciendo el producto vectorial entre los vectores M1M2 y OC, obtendremos la siguiente
expresión, donde rT es el valor del módulo del vector OC. M1M2 × OC = |M1M2| rT sen θ
En la figura 11 se puede ver que:
d = |M1M2| cos (90 – θ) = |M1M2| sen θ
y por tanto,
! = M! M! x !"
r!
Ahora necesitamos calcular M1M2 × OC:
El vector OC se puede expresar a partir de las coordenadas ecuatoriales del Sol (αs,δs) en
el instante t de la observación como (valores que se pueden obtener en efemérides astronómicas,
pero que se darán en el momento):
xs = rT cos δs cos αs
ys = rT cos δs sen αs
zs = rT sen δs
La posición de cada observador sobre la superficie de la Tierra puede expresarse como
(ver Figura 16):
x = R cos φ cos (λ + TG)
Tránsito de Venus 19 y = R cos φ sen (λ + TG)
z = R sen φ
donde φ y λ son las coordenadas geográficas (latitud y longitud) de los observadores, y TG es el
tiempo sideral de cualquier punto de la Tierra que tiene una longitud λ . En nuestro caso, para el
6 de Junio del 2012, el valor de TG(0h UT)=16h 59m 12,495s
!! = !! 0 +
360!
· ! → !! = !! (0) + 1,00273791 !
23! 56! 4,1 !
Las coordenadas del vector M1M2 se pueden encontrar fácilmente como:
X = x1 – x2
Y = y1 – y2
Z = z1 – z2
!! !! = !! + !! + !!
!! !! = !
!! + !! + !!
Y las coordenadas para el vector OC que une el centro Solar con la Tierra se podrán
considerar en función del vector unitario !, ahorrándonos el tener que conocer rT. Así, el valor
de ese vector unitario, vendrá dado por:
x = cos δS cos αS
y = cos δS sen αS
z = sen δS
De modo que volviendo a la expresión de d, ésta la podremos expresar como:
! = !! !! sin ! = !! !! ! ! = !" − !"
!
+ (!" − !")! + (!" − !")!
Figura 16 : Posición de una estrella (por ejemplo el Sol)
y de un observador en la Tierra, en coordenadas
Ecuatoriales. Créditos: M. A. Pío (IAC)
Tránsito de Venus 20 Anexo III – Leyes de Kepler.
El tema de los movimientos planetarios es inseparable de un nombre: Johannes Kepler.
La obsesión de Kepler por la geometría y la supuesta armonía del universo le permitió, luego de
varios intentos frustrados, enunciar las tres leyes que describen con extraordinaria precisión, el
movimiento de los planetas alrededor del Sol. Desde una posición cosmológica copernicana,
que en esa época era más una creencia filosófica que una teoría científica, Kepler logró esta
magnífica empresa de manera totalmente empírica, sin más teoría que su propio convencimiento
sobre el carácter fundamental (divino) de la geometría, y utilizando la gran cantidad de datos
experimentales obtenidos por Tycho Brahe.
La primera ley establece, a pesar de su autor, que los planetas describen órbitas elípticas
alrededor del Sol, que ocupa uno de sus focos. En la escala de valores geométricos de Kepler, el
círculo ocupaba un lugar privilegiado y de ahí su decepción, luego de múltiples intentos por
compatibilizar las observaciones con órbitas circulares.
1.
- Primera Ley: "La orbita que describe cada planeta es una elipse con el Sol en
uno de sus focos"
Figura 17 : Descripción de los elementos de la órbita de un objeto alrededor del Sol
Las elipses de las trayectorias son de muy poca excentricidad, de tal manera que difieren
muy poco de la circunferencia. Así por ejemplo , la excentricidad de la órbita de la Tierra es
e=0,017, y como la distancia Tierra-Sol es aproximadamente 150.000.000 de Km. la distancia
del Sol (foco) al centro de la elipse es de ae=2.500.000 Km.
La segunda ley se refiere a las áreas barridas por la línea imaginaria que une cada planeta
al Sol, llamada radio vector. Kepler observó que los planetas se mueven más rápido cuando se
hallan más cerca del Sol, pero el radio vector encierra superficies iguales en tiempos iguales. (Si
el planeta tarda el mismo tiempo en ir de A a B en la figura , que de C a D, las áreas en blanco
son iguales).
Tránsito de Venus 21 Figura 18: Representación gráfica de la segunda ley de Kepler.
2. - Segunda Ley: "Cada planeta se mueve de tal manera que el radio vector (recta que
une el centro del Sol con el planeta) barre áreas iguales en tiempos iguales"
El radio vector r, o sea la distancia entre el planeta y el foco (S) es variable, pues es
mínima en el perihelio y máxima en el afelio. Como la velocidad areal (área barrida en la unidad
de tiempo) es constante, la velocidad del planeta en su órbita debe ser variable. En virtud de esta
ley, si las áreas ASB y CSD son iguales, el arco AB será menor que el CD, lo que indica que el
planeta se desplaza más ligero en el aphelio. Es decir, su velocidad es máxima a la mínima
distancia al Sol y mínima a la máxima distancia.
Finalmente, la tercera ley relaciona el semieje mayor de la órbita, llamado R, al período
orbital del planeta P, de la siguiente manera: R3/P2 = constante. De acuerdo a esta ley, la
duración de la trayectoria orbital de un planeta aumenta con la distancia al Sol y así sabemos
que el “año” (definido como el tiempo empleado por el planeta en volver al mismo punto de su
órbita) en Mercurio tiene 88 días (terrestres), en Venus 224, en la Tierra 365 y sigue
aumentando a medida que nos alejamos del Sol. Estas leyes permiten también deducir las
distancias relativas de los objetos del sistema solar, si conocemos sus movimientos.
Determinando independientemente alguna de ellas es posible conocer sus valores absolutos.
3. - Tercera Ley: "El cuadrado de los períodos de revolución de dos planetas es
proporcional a los cubos de sus distancias medias al Sol."
Si R1, y R2 son las distancias medias al Sol de dos planetas, por ejemplo Marte y la Tierra,
y P1 y P2 son los respectivos tiempos de revolución alrededor del Sol, de acuerdo con esta ley
resulta que:
Figura 19: Relación entre los periodos y radios de las
órbitas alrededor del Sol de dos objetos, que describe
gráficamente la tercera ley de Kepler.
Tránsito de Venus 22 !!! !!!
=
!!! !!!
donde el tiempo està dado en años y la distancia en unidades astronómicas
(UA=150.000.000 Km.)
Posteriormente al enunciado de esta ley hecho por Kepler, Newton probó que en la misma
deben aparecer las masas de los cuerpos considerados, y de esta manera obtuvo la siguiente
fórmula:
!!! (! + !! ) !!!
=
!!! (! + !! ) !!!
donde M es la masa del Sol (el cuerpo situado en el foco de la Órbita), igual a 330000
veces la masa de la Tierra, y m1 y m2 son las masas de los de cuerpos considerados que se
mueven a su alrededor en orbitas elípticas. Esta expresión permite calcular la masa de un
planeta o satélite, si se conoce su periodo de traslación P y su distancia media a al Sol.
En general para los planetas del sistema solar solo las masas de Júpiter y Saturno no son
despreciables respecto a la del Sol. De esta manera , en la mayoría de los casos se considera
(M+mi) igual a: 1 masa solar y se obtiene así la expresión dada originalmente por Kepler.
Por primera vez una única curva geométrica, sin agregados ni componentes, y una única
ley de velocidad resultan suficientes para predecir las posiciones planetarias, y por primera vez
también, las predicciones son tan precisas como las observaciones.
Estas leyes empíricas recién encontraron su sustento físico y matemático en la teoría de la
gravitación universal de Newton, quien estableció el principio físico que explica los
movimientos planetarios. La construcción de este cuerpo de ideas que comienza con Copérnico
y culmina en la mecánica de Newton es un ejemplo por excelencia de lo que se considera un
procedimiento científico, al que se puede describir muy esquemáticamente de la siguiente
forma: se observa un hecho, se mide y se confecciona una tabla de datos; luego se trata de
encontrar leyes que relacionen estos datos y, finalmente, se busca un principio que sustente o
explique las leyes.
Aplicación en el caso que nos ocupa.
Las órbitas de la Tierra y Venus en torno al Sol son ligeramente elípticas y por tanto, la
relación de distancias rT/rV no se mantiene constante a lo largo del tiempo. Para saber esta
relación en el instante t de observación es necesario remitirse a la primera ley de Kepler que
dice que el Sol es uno de los focos de la elipse y que por tanto, la distancia entre el Sol y un
planeta rp(t) se obtiene como:
rp(t)=Rp (1 - ep cos Ep(t))
Tránsito de Venus 23 Figura 20 : Sección de la elipse que muestra excéntrica (E) y verdadera (θ) anomalía. Créditos M. A. Pío (IAC)
donde Rp es el semieje mayor de la órbita, ep la excentricidad y Ep(t) la anomalía
excéntrica (ángulo medido desde el centro de la elipse, ángulo formado entre la proyección del
planeta en el círculo llamado “auxiliar”, y el eje mayor elipse, ver Figura 20) en el instante t.
Según esto:
rT/rv=[RT (1 - eT cos ET)] / [RV (1 - eV cos EV)]
La tercera ley de Kepler relaciona los semiejes mayores de las órbitas con los períodos de
revolución Pp:
(RT / RV)3 = (PT / PV)2
, de manera que:
rT/rv=(PT / PV)2/3 (1 - eT cos ET) / (1 - eV cos EV)
donde, obtenemos una relación que nos permite conocer el valor del cociente rT/rV en
cualquier instante de tiempo, pues tanto eT, eV, así como ET y EV, no son constantes sino que
varían con el tiempo. Es cierto que los valores de la excentricidad de la órbita varían muy poco,
por lo que se suelen considerar constantes, por lo que sólo conociendo los valores de la
anomalía excéntrica de ambos planetas para todo t, se puede entonces calcular la relación rT/rV
para un t determinado
Tránsito de Venus 24 ANEXO IV: Cálculo de la rotación/traslación de las imágenes.
Como hemos comentado en el apartado 5.2.1 si tomamos una imagen del Sol desde un
lugar sobre la superficie terrestre en un determinado instante de tiempo t, y en ese mismo
instante tomamos otra imagen desde otro lugar lo suficientemente alejado del primero, éstas dos
imágenes aparecerán rotadas un cierto ángulo θ qué dependerá directamente de la separación de
esas dos posiciones sobre la Tierra. Si además, el apuntado de los telescopios no es exactamente
igual las imágenes también presentarán una traslación. Debemos recordar que las imágenes se
tomarán con la misma instrumentación y, por tanto, presentarán la misma escala.
Sistemas de Coordenadas S y S’.
Vamos a suponer dos sistemas de coordenadas. A uno lo llamaremos S’ y estará situado
en el centro del Sol y el otro será S y, por comodidad, lo situaremos en el extremo inferior
izquierdo de la imagen (ver Figuras 21 y 22), realmente lo importante es que el sistema S sea el
mismo para ambas imágenes.
Figura 21: Diagrama de la representación gráfica del sistema utilizado. Créditos: M. A. Pío (IAC)
Las ecuaciones de transformación por traslación entre ambos sistemas serán:
x’i1 = xi1 - xc1 ; x’i2 = xi2 - xc2
y’i1 = yi1 - yc1 ; y’i2 = yi2 - yc2
donde (xc1,yc1), (xc2,yc2) son las coordenadas del centro del Sol en Sapporo y Cairns,
respectivamente, en el sistema de coordenadas S, (xi1,yi1), (xi2,yi2) son las coordenadas de un
punto medidas en la imagen, sistema S, y (x’i1,y’i1), (x’i2,y’i2) son las coordenadas de un punto
según el sistema de referencia S’ centrado en el Sol.
Tránsito de Venus 25 Medición del ángulo θ.
Una vez ya tenemos todos los puntos referidos al sistema de coordenadas S’ centrado en
el Sol, pasaremos a calcular el valor del ángulo θ calculando la diferencia entre los ángulos que
forman el vector T’2 referente a la mancha en la imagen de Cairns, y el que forma T’1 en la
imagen de Sapporo, a través de la relación (producto escalar):
T! ! · T! ! = T! ! · T! ! · cos θ
T! ! · T! ! = !′!! · ! ! !! + !′!! · ! ! !!
⟹ cos ! =
!′!! · ! ! !! + !′!! · ! ! !!
!
!′!!! + !′!!! ·
!
!′!!! + !′!!!
Cálculo de Δπ en el sistema de coordenadas S.
Finalmente calcularemos el valor de la distancia Δπ referida al sistema S, cuyo cero se
encuentra situado en la esquina inferior izquierda de la imagen.
Figura 22: Diagrama de vectores para cada punto según los sistemas S’ (centro del Sol) y S
(extremo inferior izquierdo imagen). Créditos M. A. Pío (IAC)
Según la Figura 22, podemos expresar los vectores T1, T2, R1 y R2 en función de los
vectores del sistema S’ centrado en el Sol, y del vector c que une el origen de coordenadas de S
con el de S’, como:
!! = ! + !! ! !! = ! + !! !
Por otro lado, la expresión de Δπ que tenemos un poco más arriba, también se puede
expresar en función de las coordenadas, de manera que el valor total sea:
Δ! =
!
Δ!! ! + Δ!! !
Tránsito de Venus 26 Así:
Δ!! = !!" − !!! = !!" − !! + !! Δ!! = !!" − !!! = !!" − !! + !!
donde (!!" , !!" ) es la coordenada de la sombra de Venus en Cairns en el sistema de
referencia S’ rotado el ángulo ! , aplicando las ecuaciones de transformación por rotación y
traslación a las coordenadas en S quedará:
Δ!! = !!" − !!! = !! − !!! cos ! + !! − !!! sin ! − !! + !!!
Δ!! = !!" − !!! = − !! − !!! sin ! + !! − !!! cos ! − !! + !!!
donde (!! , !! ) y (!! , !! ) son las coordenadas de la sombra de Venus en las imágenes
de Sapporo y Cairns, respectivamente, mientras (xc1,yc1), (xc2,yc2) son las coordenadas del centro
del Sol en Sapporo y Cairns, respectivamente, todo referido al sistema de coordenadas S.
Tránsito de Venus 27 ANEXO V: Glosario.
Blurring (emborronamiento).
Se dice cuando una imagen no es clara y parece no estar bien enfocada. Ésto es debido al
seeing atmosférico y la difracción del Telescopio.
Centro de masas.
El centro de masas o barycentro de un cuerpo, es un punto del espacio donde, para la
mejora de cálculos, toda la masa del cuerpo puede asumirse que se encuentra concentrada en ese
punto.
Conjunción Interior.
Una conjunción de un planeta inferior que se produce cuando el planeta se alinea
directamente entre la Tierra y el Sol.
Conjunción Superior.
Una conjunción que se produce cuando un planeta superior pasa por detrás del Sol y está
en el lado opuesto del Sol desde la Tierra.
Difracción
Es la abilidad de las ondas de doblarse alrededor de las esquinas. La difracción de la luz
establece su naturaleza ondulatoria.
Eclipse
Es el oscurecimiento de un cuerpo celeste causado por la interposición de otro cuerpo
entre este cuerpo y la fuente de iluminación.
Eclíptica
La eclíptica es el camino que el sol parece seguir a través de la esfera celeste en el
transcurso de un año. De hecho, es el plano definido por la órbita terrestre alrededor del sol.
Filtro
Un filtro es un dispositivo óptico que bloquea ciertos tipos de luz y otros los transmite. En
astronomía los filtros se utilizan principalmente para estudiar la luz desde una fuente en un color
determinado, es decir, en una región del espectro electromagnético particular, que pueden
proporcionar información sobre la química del objeto.
Flujo
El flujo es la medida de la cantidad de energía emitida por un objeto astronómico en
función de una cantidad fija de tiempo y área.
Gravedad.
La gravedad es una fuerza de la naturaleza que hace que dos cuerpos se atraigan
mútuamente entre sí. Cuanto más masivo es un objeto, mayor es la fuerza de la gravedad.
Latitud
La Latitud es la distancia angular hacia el Norte o el Sur, desde el ecuador celeste, de un
objeto celeste, incluyendo la Tierra.
Limbo
El límite exterior del disco aparente de un cuerpo celeste.
Tránsito de Venus 28 Longitud
Longitud, en la Tierra, es una coordenada geográfica que especifica la posición este-oeste
de un punto sobre la superficie de la Tierra. Se trata de una medida angular, generalmente
expresada en grados, minutos y segundos. En concreto, es el ángulo entre un plano que contiene
el Meridiano de Greenwich y un plano que contiene el Polo Norte, Polo Sur y el lugar en
cuestión. Si la dirección de la longitud (este u oeste) no se especifica, los valores positivos de
longitud se encuentran al este del meridiano de Greenwich, y los valores negativos están al oeste
del Meridiano de Greenwich. El homólogo celeste más cercano a la longitud terrestre es la
ascensión recta.
Lunas de Galileo.
Nombre dado a las cuatro lunas más grandes de Jupiter, Io, Europa, Calisto y Ganímedes.
Meridiano
El meridiano es una línea imaginaria norte-sur en el cielo que pasa a través de cenit del
observador.
Micrón o Micrómetro
Es la millonésima parte de un metro.
Minutos de Arco.
Es una unidad de medida angular igual a sesentavo (1/60) de un grado o (π/10800)
radianes. Un grado se define la (1/360) parte de una rotación, así que un minuto de arco es la
1/21600 parte de una rotación.
Nodo
Uno de los dos puntos de la esfera celeste asociada a la intersección del plano de la órbita
y un plano de referencia. La posición del nodo es uno de los elementos orbitales habituales.
Nucleosíntesis
Es la creación de un elemento nuevo a través de reacciones nucleares. La nucleosíntesis
tiene lugar en las estrellas. También tuvo lugar justo después del Big Bang.
Ocultación
La ocultación es un evento que ocurre cuando un cuerpo celeste oculta o esconde otro.
Por ejemplo, un eclipse solar es una ocultación del Sol por la Luna.
Oposición
Un planeta está en oposición cuando la Tierra se encuentra exactamente entre el planeta y
el sol.
Órbita
El término órbita se refiere a la ruta que sigue un objeto en torno a un objeto más masivo,
o al centro de masas común.
Paralaje
Paralaje es el cambio de posición aparente de dos objetos vistos desde distintas
ubicaciones. Es causada sólo por el movimiento de la Tierra en su órbita alrededor del sol.
Tránsito de Venus 29 Parsec
Un parsec es una unidad de distancia de uso común en la astronomía y la cosmología, y
es igual a cerca de 3.262 años luz, o 3.09 x 1016 metros. Es la distancia a la que una estrella tiene
una paralaje de 1 segundo de arco.
Periastro.
También se llama periapsis. Es el punto en una órbita elíptica de dos objetos, donde la
distancia entre los cuerpos es mínima. Es el contrario del apoastro.
Perigeo.
El perigeo es el punto de la órbita de la Luna u otro satélite, en el que está más cerca de la
Tierra.
Perihelio
El perihelio es el punto de la órbita de un planeta u otro cuerpo en el que está más cerca
del Sol. La Tierra está en su perihelio (la Tierra está más cerca del Sol), en enero.
Planeta
Un planeta es un cuerpo celeste que orbita una estrella o un remanente estelar, que es lo
bastante masivo para ser redondeado por su propia gravedad, y no es lo suficientemente masivo
como para causar la fusión termonuclear y por lo tanto no brilla por sí mismo.
Planeta Inferior.
Un planeta que orbita entre la Tierra y el Sol. Mercurio y Venus son los únicos dos
planetas inferiores en nuestro sistema solar.
Planeta Superior.
Un planeta que existe fuera de la órbita de la Tierra. Todos los planetas de nuestro
sistema solar son superiores a excepción de Mercurio y Venus.
Refracción
La refracción es el cambio en la dirección de una onda debido a un cambio en su
velocidad
Resolución (espacial)
La resolución espacial es la capacidad de un aparato montado sobre un telescopio para
diferenciar entre dos objetos en el cielo que están separados por una distancia angular pequeña.
Cuanto más cercano se encuentren dos objetos entre si, si eel instrumento puede verlos
como dos objetos distintos, mayor será el poder de resolución espacial del mismo.
Resolución (espectral o de frecuencias)
La resolución espectral es la capacidad de un aparato montado sobre un telescopio para
diferenciar dos señales luminosas que difieren en frecuencia por una pequeña cantidad. Cuanto
más cerca están dos señales en frecuencia entre si, si el instrumento puede aún separarlas como
dos frecuencias distintas, mayor es su resolución espectral.
Revolucion
La revolución es el movimiento de un objeto alrededor de otro.
Seeing
El término seeing en la astronomía se utiliza para describir el efecto perturbador de las
turbulencias en la atmósfera de la Tierra en la luz estelar entrante.
Tránsito de Venus 30 Segundos de Arco.
Un segundo de arco es igual a la 1/60 parte de un minuto de arco o 1/3600 parte de un
grado. Es 1/1296000 de un una rotación, o (π/648000) radianes.
Tiempo Universal.
El tiempo universal (abreviado UT o UTC) es el mismo que el tiempo medio de
Greenwich (abreviado GMT), es decir, el tiempo solar medio en el Meridiano de Greenwich,
Inglaterra (longitud cero).
Tránsito
El tránsito es cuando un objeto más pequeño astronómico pasa por delante de uno más
grande. Durante este tiempo, el objeto más pequeño parece estar cruzando el disco del más
grande. El tránsito es también el paso de un cuerpo celeste a través de meridiano del observador.
Unidad Astronómica (UA).
La unidad astronómica es una unidad de longitud utilizada por los astrónomos, por lo
general para describir las distancias dentro de los sistemas planetarios como nuestro Sistema
Solar. Una UA es igual a 149.597.871 kilometros, y corresponde a la distancia media entre la
Tierra y el Sol.
Tránsito de Venus 31