Corriente eléctrica - Universidad de Sevilla

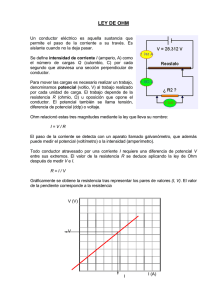
Corriente eléctrica
Física II
Grado en Ingeniería de
Organización Industrial
Primer Curso
Joaquín Bernal Méndez
Curso 2011-2012
Departamento de Física Aplicada III
Universidad de Sevilla
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
2/39
Introducción
Existe corriente eléctrica en situaciones
donde aparece un flujo de carga a través de
una región del espacio
Flujo de carga por el interior de un hilo conductor
Flujo de electrones en un tubo de imagen
Rayos
3/39
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
4/39
Corriente eléctrica
Flujo de cargas eléctricas que por unidad de
tiempo atraviesan un área transversal
Sea ΔQ la carga total
que atraviesa A en un Δt
Q
Intensidad de corriente media
t
Q dQ
Intensidad de
I  lim

corriente instantánea
t 0 t
dt
Im 
Unidades:
amperio (A)
1 A = 1 C/s
5/39
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
6/39
Sentido de la corriente
Para indicar el sentido del flujo de carga se utiliza el signo de la
intensidad de corriente
Se asigna signo positivo al sentido de flujo de las cargas positivas
I 0
A
¿y si los portadores llevan carga negativa?
A
Equivale a:
A
I 0
Conductores metálicos: los electrones son las cargas en movimiento
y, por tanto, el sentido de la corriente es el contrario al del
movimiento de los electrones
7/39
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
8/39
Corriente en metales
En ausencia de campo eléctrico los electrones se
mueven al azar por agitación térmica con una
velocidad del orden de 106 m/s
En esta situación no hay, por tanto, corriente neta
Cuando aplicamos un campo eléctrico:
Aceleración inicial en sentido opuesto al campo
choques con los iones fijos de la red metálica
La consecuencia es una velocidad adicional
promedio en el sentido opuesto al campo
Esta velocidad adicional recibe varios nombres:
velocidad de desplazamiento ó velocidad de deriva
ó velocidad de arrastre
9/39
Relación entre I y la velocidad
de deriva
Cable metálico de sección A
Densidad numérica (n): densidad de
partículas libres cargadas por
unidad de volumen
q: carga de cada partícula libre
vd : velocidad de deriva
¿Cuántas partículas atraviesan A en un Δt?
Todas las que están a una distancia de A menor que vdΔt
Es decir, las incluidas en un volumen V= AvdΔt
Número de partículas = nV= nAvdΔt
Carga total que atraviesa en Δt : ΔQ=qnAvdΔt
Intensidad de corriente:
Si hay varios tipos de
Q
I  lim
t 0
t
 qnAvd
portadores se suman
sus aportaciones
10/39
Ejemplo numérico (I)
Se trata de ver el orden de magnitud que tiene la
velocidad de deriva en la práctica
Consideramos un cable de cobre de calibre 14 que
soporta una intensidad de 1 A
vd 
I  qnAvd
I
nqA
Donde:
q  e  1.6  1019 C
r  0.815 mm (calibre 14)
A  r 2
11/39
Ejemplo numérico (II)
n es la densidad de átomos de cobre, que se puede calcular:
n
Cu NA
M
Se obtiene:n
Entonces:
vd 
Donde:
Cu  8.93 g/cm3
M  63.5 g/mol
N A  6.02  1023 átomos/mol
 8.47  1028 átomos/m3
I
 3.54  105 m/s  0.0354 mm/s
nqA
¿Qué distancia recorre un electrón en una hora?
3.54  105
3600 s
m
 0.13 m  13 cm
 1 hora
1 hora
s
12/39
Cuestión
Tal como se muestra en el anterior ejemplo
numérico la velocidad de deriva suele ser
bastante pequeña (del orden de centímetros ó
decenas de centímetros por hora)
Entonces, ¿Cómo es posible que al accionar
el interruptor de la luz una bombilla se
encienda instantáneamente?
13/39
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
14/39
Densidad de corriente
Se define la densidad de corriente como la
intensidad por unidad de área transversal al
movimiento de los portadores
I
J   nqvd
A 
En general es una magnitud vectorial: J  nqvd

La I que atraviesa una superficie es el flujo de J :
 
I   J  dA

I  nqAvd
nˆi
J
Ai
S
Para una
 superficie plana:
 
Si J es uniforme: I  J  A
Si además son paralelos: I 
JA
15/39
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
16/39
Concepto de resistencia (I)
Hasta ahora hemos estudiado la corriente eléctrica sin
entrar a analizar en sus causas
El flujo de cargas suele venir producido por un campo
eléctrico
Ejemplo: alambre conductor recto

E
Va
Va  Vb   
Vb
a
b
A
 
E  dl  EL
Si la corriente es estacionaria se
suele cumplir que E es uniforme
L
Una situación dinámica se dice que es estacionaria
cuando no existe variación con el tiempo de las
magnitudes físicas involucradas en el fenómeno
17/39
Concepto de resistencia (II)
Sea un alambre conductor que transporta una
corriente I como respuesta a una diferencia de
potencial Va-Vb=V entre dos puntos.
Se define la resistencia eléctrica de ese hilo conductor
de la siguiente
forma:

Va
E
Vb
R
A
V
I
L
En general R=R(V)
Depende del material
Depende de la geometría (A,L)
18/39
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
19/39
Ley de Ohm
Existen materiales para los cuales, dentro de un rango
de valores del campo eléctrico aplicado, se cumple
que
R  R(V )
Se dice que dichos materiales cumplen la
Ley de Ohm: V=IR
con R constante
Se denominan materiales óhmicos
Son óhmicos la mayor parte de los metales para valores
usuales del campo eléctrico
Notas importantes:
La Ley de Ohm no es una ley física: sólo la cumplen
determinados materiales en determinadas circunstancias
La Ley de Ohm no es la ecuación V=IR, sino el hecho de que
se cumpla para un valor de R independiente del V aplicado
20/39
Ley de Ohm: interpretación
gráfica
1R
Material óhmico
Material NO óhmico
La pendiente (1/R) no cambia
21/39
Ley de Ohm: enunciado general
El enunciado de la Ley de Ohm que hemos presentado
es válido para hilos conductores
Hay otra forma más general de enunciar la Ley de
Ohm:
Se dice que un material es óhmico cuando


en todos sus puntos se cumple que J  E
Donde  = conductividad del material
Unidades de 1/(Ωm)=S/m; donde S=1/Ω es el
símbolo de siemens
La conductividad es una propiedad del material, no
depende de su forma o tamaño (geometría).
22/39
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
23/39
Resistencia de un hilo
conductor
Supongamos un hilo conductor:
Va

E
A
Vb
Va  Vb  V  EL
I  JA
L


EL

R
(Ley
de
Ohm):
J  E
EA
R
R
V EL

I
JA
L
L

A
A
=1/ es la resistividad del material
Unidades de Ωm
La conductividad (o resistividad) caracteriza al
material, mientras que la resistencia es propia del
dispositivo
24/39
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
25/39
Dependencia de la resistividad
con la temperatura
En general la resistividad de un material cambia con T
En la mayoría de los metales la relación es lineal en
un rango amplio de temperaturas:
  0 1  (T  T0 ) 
: resistividad a 20ºC
: coeficiente de temperatura
Para un hilo conductor:
R

1 
0 T
(Unidades: K-1)
L
 R  R0 1  (T  T0 ) 
A
Donde asumimos que L y A no cambian mucho con T
26/39
Ejemplo
Resistividad en función de la temperatura para el cobre
27/39
Tabla de resistividades y
coeficientes de temperatura
Material
Oro
Plata
Cobre
Hierro
Plomo
Carbono
Manganina
Silicio
Madera
0 (Ωm) 20ºC
2.44 × 10-8
1.6 × 10-8
1.7 × 10-8
10 × 10-8
22 × 10-8
3500 × 10-8
44 × 10-8
640
108 - 1014
 (K-1) 20ºC
3.4 × 10-3
3.8 × 10-3
3.9 × 10-3
5.0 × 10-3
4.3 × 10-3
-0.5 × 10-3
0.02 × 10-3
-7.5 × 10-2
28/39
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
29/39
Energía en el proceso de
conducción: efecto Joule
V

E
V
b
Cuando los portadores se desplazan a
por el interior del conductor
A
disminuye su energía potencial
Las colisiones con los iones reticulares causan que en
estado estacionario los portadores viajen con una
velocidad de deriva constante → no hay cambio de
energía cinética de los portadores
¿Dónde va entonces la energía potencial que pierden
los portadores?
Respuesta: se acumula en forma de energía interna
del material → aumento de temperatura
El aumento de temperatura que experimenta un material conductor
cuando transporta una corriente se denomina efecto Joule
30/39
Potencia disipada por
efecto Joule (I)
Consideramos un segmento de alambre
que transporta una corriente estacionaria
Q es la carga libre en un segmento L
Cuando transcurre un tiempo t la carga
se desplaza un poco hacia la derecha
Disminución de energía potencial:
equivale a que un Q se desplace del
extremo izquierdo al derecho:
U  Q(Vb  Va )  QV
Potencia perdida por la carga Q:

U Q

V  IV
t
t
Por tanto, la potencia disipada por efecto Joule es:
P  IV
31/39
Potencia disipada por
efecto Joule (II)
La potencia disipada es el producto de la disminución
de energía potencial por unidad de carga (V ) por el
flujo de carga por unidad de tiempo (I)
Esto puede aplicarse a cualquier dispositivo de un
circuito
En un conductor de resistencia R podemos utilizar
V=IR para escribir:
V2
P  IV  I R 
R
2
32/39
Índice
Introducción
Corriente eléctrica
Sentido de la corriente
Corriente en conductores: velocidad de deriva
Densidad de corriente
Resistencia eléctrica
Ley de Ohm
Resistencia de un alambre conductor
Dependencia con la temperatura
Potencia disipada por efecto Joule
FEM y baterías
33/39
FEM y baterías
Para mantener una corriente en un conductor
es necesario suministrar energía eléctrica
Fuente de fem (fuerza electromotriz). Ejemplos:
Pila: Energía química
energía eléctrica
Generador: energía mecánica
energía eléctrica
34/39
Fuente de fem (I)
Modelamos un hilo de corriente como una resistencia
Cuando la carga recorre la R su energía potencial
electrostática baja (porque pasa a un potencial menor)
Para cerrar el circuito hace falta un dispositivo que
pase la carga de Vd a Vc
Le suministra energía potencial electrostática U  QV
Vc
+
I
V  Vc  Vd
Q
t
-
Vd
35/39
Fuente de fem (II)
Fem (fuerza electromotriz) = trabajo por unidad de
carga que realiza la fuente
No es una fuerza: sus unidades son voltios (V)
Se suele usar el símbolo ε
36/39
Batería ideal
En una batería ideal el trabajo por unidad de carga
coincide con el necesario para elevar el potencial de la
carga:
W
U QV



 V
Q Q
Q
Es decir, la fem es igual a la diferencia de potencial
entre los bornes de la batería
I
V 

R
R
37/39
Batería real
Cuando se mide ∆V entre los 
bornes de una batería se
comprueba que decrece
linealmente con I:
V    Ir
Parte de la energía que suministra una batería real se
disipa en su resistencia interna (r)
  Ir  V  Ir  IR
I

Rr
38/39
Resumen
La corriente eléctrica se define como el flujo de carga que por unidad de tiempo
atraviesa la unidad de área transversal
En metales los portadores son electrones, que bajo condiciones de corriente
estacionaria, se mueven con una velocidad de deriva constante.
La velocidad de deriva toma típicamente valores del orden de centímetros ó
decenas de centímetros por hora
La densidad de corriente es un campo vectorial cuyo flujo a través de una
determinada superficie nos da la intensidad de corriente que la atraviesa
La resistencia eléctrica de un hilo conductor se define como el cociente entre la
diferencia de potencial entre sus extremos y la intensidad que lo atraviesa
La resistencia de un conductor óhmico no depende del voltaje aplicado, pero
suele variar con la temperatura de forma aproximadamente lineal
El aumento de temperatura que experimenta un material conductor cuando
transporta una corriente se denomina efecto Joule
La potencia disipada por efecto Joule es: P=IV
Una fuente de fem es el dispositivo que suministra la energía que es necesaria
para mantener una corriente estacionaria en un conductor
La fem (ε) se mide en voltios y es el trabajo por unidad de carga realizado por
la fuente de fem
39/39