Geometría Analítica
Anuncio

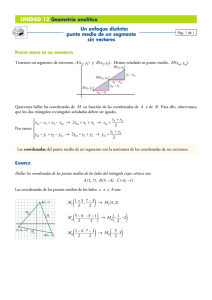
Geometría Analítica … PARA LA CLASE GEOMETRÍA ANALÍTICA La Geometría Analítica hace uso del Álgebra y la Geometría plana. Con ella expresamos y resolvemos fácilmente problemas geométricos de forma algebraica, siendo los sistemas de coordenadas cartesianas un elemento clave. DISTANCIA ENTRE DOS PUNTOS Sean las coordenadas de dos puntos cualesquiera A (x 2; y2) y B (x1; y1); la distancia entre ellos es igual a la longitud del segmento AB. Así: y2 d(A,B) x1 A (x2;y2) y2 – y1 x2 B (x1;y1) y1 x1 – x2 01. Encuentra la distancia entre cada par de puntos. A (-4; 4) y B (4; 4 ) C (3; -4) y D (3; 3) E (2; -2) y F (6; 1) G (2; 1) y H (7; 2) 8 7 5 26 02. Si la distancia del origen al punto P (3; x – 2) es 5. Calcula el valor de x. x = -2, x = 6 03. La distancia entre dos puntos de igual abscisa es 8. Si uno de los puntos tiene ordenada -3, halla la ordenada del otro punto. y = -11, y = 5 04. Uno de los extremos de un segmento rectilíneo de longitud 5 es el punto P (3;-2). Si la abscisa del otro extremo es 6, halla su ordenada. y = -6, y = 2 05. Encuentra un punto sobre el eje Y que sea equidistante de los puntos (5; -5) y (1, 1). (0; -4) 06. Los vértices de un triángulo equilátero son los puntos A (-1; 1), B (3; 1) y C (x; y). Halla las coordenadas del punto C. 1;1 2 3 07. La base de un triángulo isósceles es el segmento que une los puntos (-1; -3) y (3; 1). Si la abscisa del tercer vértice es -4 encuentra la ordenada. y=4 08. La distancia entre los puntos A (-1; n) y B (5n + 1; 7) es igual a 13. Halla el valor de n, si A pertenece al segundo cuadrante. n=2 Javier Trigoso/Freddy Liñán Página 1 Geometría Analítica 09. El punto (x; -5) se encuentra dos veces más lejos del punto (-5; 4) que del punto (10; -1). Halla el valor de x. x = 7, x = 67/4 DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA 10. Si la distancia de A (2; 2) a B (5; b) es 5 y la distancia de este Si A (x2; y2) y B (x1; y1) son los extremos de un segmento de recta, es posible encontrar las coordenadas de un punto P(x; y) que divida al AP segmento AB en una razón dada por la expresión r , así: PB último a C (c; 3) es 29 . Halla la distancia del punto A al punto C. (b < 0 y c ≠ 3) d 26 A 11. La longitud del segmento MN es 13; su origen está en el punto M (3; -2), la proyección sobre el eje de abscisas es 12. Halla las coordenadas del otro extremo del segmento, si forma con el eje de ordenadas un ángulo dado. (-9; -7) 12. Encuentra las coordenadas del centro de la circunferencia circunscrita al triángulo de vértices A (10; 2), B (9; -3) y C (-8; -10). (-3; 2) ar P B (x1;y1) y y1 x1 Javier Trigoso/Freddy Liñán y2 a x x2 Página 2 Geometría Analítica … PARA LA CLASE 01. Los extremos de un segmento son los puntos A (-2; -5) y B (7; 7). Determina un punto C que divida al segmento AB en la razón de 4 a 5. (2; 1/3) 02. Dados los puntos A (-2; 1) y B (8; 11). Halla las coordenadas de un punto P que divida al segmento AB en la razón de 2 a 3. (2; 5) 03. Si en el gráfico: AP = 2PB, calcular (x + y). A (–1; 5) 08. Determina las coordenadas de los puntos que dividen al segmento AB en tres partes iguales, sabiendo que A (-1; 7) y B (11; -8). (3; 2), (7; -3) 09. Los vértices del triángulo ABC son los puntos A (1; 0), B (5; 4) y C (-3; 5). Halla la distancia del baricentro al vértice A. 3 10. Los puntos A (2; 5), B (4, 2) y C (a; b) son los vértices de un triángulo. Halla las coordenadas del vértice C, si el baricentro del triángulo ABC es el punto G (2; 3). 11. ¿Hasta qué punto debe prolongarse el segmento que une los puntos A (1; -1) y B (4; 5), para que su longitud se triplique? (10; 17) P (x; y) B (5; –1) 04. Sobre una recta se ubican los puntos A (-4; -1), B, C y D (8; 5), BC CD tal que AB . Calcula las coordenadas de los puntos B y C. 2 3 B (-2; 0), C (2; 2) 12. El punto de intersección M, de las medianas de un triángulo ABC, se encuentra en el eje de abscisas, dos de sus vértices son los puntos A (2; -3) y B (-5; 1). El tercer vértice C está en el eje de ordenadas. Determina las coordenadas de los puntos M y C. M (-1; 0), C (0; 3) 05. Dados los puntos A (-2; a), B (b; 10) y C (0; 4). Halla a + b si se sabe AC 1 que 5 BC 2 06. Determina las coordenadas del baricentro del triángulo ABC de vértices A(5; 3), B(-4; 1) y C(2; 2). (1; 2) 07. Dos de los vértices de un triángulo son A(–4; 6) y B(–3; –6). Calcula la suma de las coordenadas del tercer vértice, sabiendo que las medianas de dicho triángulo se cortan en el punto (2; 6) 31 Javier Trigoso/Freddy Liñán Página 3 Geometría Analítica PUNTO MEDIO DE UN SEGMENTO … PARA LA CLASE Si A (x2; y2) y B (x1; y1) son los extremos de un segmento de recta, el punto medio de dicho segmento es el punto M (x; y), que divide en dos segmentos AM y MB de igual longitud. Así: 01. ¿Cuál es la suma de coordenadas del punto medio del segmento cuyos extremos son A (1; 7) y B (-3; 1). 3 A (x2;y2) 03. Halla las coordenadas del punto C, sabiendo que B (2; -2) es el punto medio de AC, A (-3; 1). (7; -5) M y2 y B (x1;y1) x 04. Determina las coordenadas del punto medio del segmento AB. A (m + 1; -3) y B (1 - m; 5) (1; 4) 05. Si el punto medio del segmento cuyos extremos son A (x – 5; y + 3) y B (x – 1; y + 1) es M (4; 5). Calcula x + y. 10 y1 x1 02. El punto medio del segmento AB es M (-7; 2). La abscisa de A es 5 y la ordenada de B es -9. Encuentra las coordenadas de los puntos A y B. (5; 13), (-19; -9) x2 06. Hasta qué punto debe prolongarse el segmento que empieza en A (5; -2) y termina en B (-3; 7) para que su longitud se duplique. (-11; 16) 07. Si los vértices de un triángulo son los puntos A (1; 4), B (3; -9) y C (-5; 2). Calcula la longitud de la mediana relativa al lado AC. 13 08. Determina la distancia del punto (a; b) al origen de coordenadas, sabiendo que (1; 2) es el punto medio del segmento formado por (a; 1) y (-2; b) 5 Javier Trigoso/Freddy Liñán Página 4 Geometría Analítica ÁNGULO DE INCLINACIÓN Y PENDIENTE DE UN SEGMENTO El ángulo de inclinación (α) de un segmento, es el ángulo que forma el segmento (o su prolongación) con el eje X, medido en sentido antihorario y considerando al eje X como lado inicial. La pendiente (m) es la tangente del ángulo de inclinación. A (x2;y2) y2 y2-y1 y1 01. Calcula la pendiente de la recta que pasa por los puntos: A (2; 1) y B (7; 2) C (3; -4) y D (3; 3) (2; -2) y F (6; 1) 1/5 ∞ 3/4 02. Los vértices de un triángulo son los puntos A (2; -2), B (-1; 4) y C (4; 5). Calcula el producto de las pendientes de los tres lados. -7/5 03. Si el punto (-3; y) es colineal con los puntos (1; 3) y (0; 2); halla el valor de y. -1 04. Si los puntos A (-5; 2), B (a; 2a) y C (7; 8) son colineales, encuentra el valor de a. 3 05. Se tiene un rectángulo ABCD cuyos vértices son A (4; 1), B (9; 1) y C (9; 5). Determina La pendiente de la recta que contiene a la diagonal BD. -4/5 B (x1;y1) α α … PARA LA CLASE x2-x1 06. Los vértices de un triángulo son los puntos (2; - 2), (- 1; 4) y (4; -5). Calcula la pendiente de cada uno de sus lados. -2; -9/5; -3/2 x1 x2 07. Tres vértices consecutivos de un paralelogramo son los puntos (1; -2), (7; 3) y (-2; 2) Encuentra el cuarto vértice. (-8; -3) 08. Dos vértices de un cuadrado ABCD son A(–1; 3)y B(–1; –3). Si el vértice C está en el cuarto cuadrante, calcula la suma de las coordenadas de los vértices C y D. 10 Javier Trigoso/Freddy Liñán Página 5 Geometría Analítica 09. En el gráfico, hallar el valor de “b”. 05. Del gráfico mostrado, calcular (a + b) Y (13; b) (2; 4) 37° X 10. En la figura, hallar m + n. Y M(3; 3) (7; –1) 06. Si los vértices de un triángulo son los puntos A (1; 1), B (–3; 7) y C (5; 5), calcular la longitud de la mediana relativa al lado BC. (0; 8) A) P (m;n) 8° (a; b) A) 2 B) 3 C) 4 D) 6 37 A) 6 3 01. ¿Cuál es la distancia entre P (–1; 2) y Q (3; 4)? B) 2 5 C) 10 D) 2 10 02. ¿Cuál es la distancia entre P (4; –1) y Q (–1; 2)? A) 17 B) 29 C) 37 D) 34 03. ¿Cuál es la suma de coordenadas del punto medio del segmento cuyos extremos son A (–1; 5) y B (7; 3)? A) 7 B) 6 C) 5 D) 4 04. ¿Cuál es la suma de coordenadas del punto medio del segmento cuyos extremos son P (7; –1) y Q (3; 7)? A) 2 B) 4 C) 6 D) 8 Javier Trigoso/Freddy Liñán C) 5 D) 6 B) 10 3 C) 8 3 D) 4 3 08. Si los vértices de un triángulo son los puntos A (–1; 1), B (3; 5) y C (5; –1), ¿cuál es la longitud del mayor lado? … PARA LA CASA 5 26 07. Si dos vértices de un triángulo equilátero son los puntos A (1; 3) y B (3; –3), ¿cuál es la superficie del triángulo? X A) B) A) 2 10 B) 4 2 C) 3 5 D) 2 5 09. Calcular las coordenadas de los puntos que trisecan al segmento cuyos extremos son: A (3; 8) y B (–3; –9). 10 10 ;1 , 3 3 5 5 3 3 A) 1; C) 2 ; , ; 3 10 7 B) 1; , 1; 3 3 5 7 D) ;1, ;2 3 3 10. Si dos vértices consecutivos de un cuadrado son los puntos A (–3; 1) y B (1; 3), ¿cuál es el perímetro del cuadrado? A) 2 5 B) 4 5 C) 8 5 D) 16 5 Página 6 Geometría Analítica 11. Calcular las coordenadas de un punto “P” que divide a un segmento AB en la razón AP/PB = 5/7, además A (–8; 4) y B (3; –3) 13 41 ; 12 12 C) 41 13 ; 12 12 D) A) B) 13 41 ; 12 12 17. Halle el área del triángulo cuyos vértices son los puntos: A (1; 1), B (3; 5) y C (7; 0) A) 11u2 B) 15 u2 C) 16 u2 D) 13 u2 41 13 ; 12 12 12. Estoy en el punto (–5; –2), avanzo a la derecha ocho unidades (paralelo al eje “x”), luego avanzo cuatro unidades hacia arriba (paralelo al eje “y”), después avanzo a la derecha siete unidades (paralelo al eje “x”) y finalmente cuatro unidades hacia arriba, ¿en qué punto me encuentro ahora? A) (4; 8) B) (10; 6) C) (6; 9) D) (6; 8) 13. Del segmento mostrado, calcular las coordenadas del punto “A”, si: AM = 4MB. A A) (13; –25) B) (5; –3) C) (–25; 13) D) (–25; –13) 16. ¿Cuál es la suma de las coordenadas del baricentro del triángulo, cuyos vértices son los puntos: A (1; 5), B (3; –1) y C (5; 5)? A) 3 B) 4 C) 5 D) 6 M (–1; 1) B (5; –2) 14. El segmento de extremos A (–7; 1) y B (15; 10), se divide en seis partes iguales, calcular la suma de las abscisas de los puntos de división. A) 14 B) 16 C) 18 D) 20 18. Un punto “P” está ubicado en el primer cuadrante, su abscisa es 12. Si la distancia del punto “P” al origen es 13 unidades, ¿cuál es la ordenada de P? A) 5 B) 5 C) 10 D) –5 19. Los puntos A (–6; –2), B (2; 4) y C (2; –2), son los vértices del triángulo ABC, ¿cuál es su perímetro? A) 24 u B) 23,6 u C) 114 u D) 48 u 20. Los puntos A (–6; –2), B (–2; 6) y C (4; –4), son los vértices del triángulo ABC, si CN es mediana del triángulo (N AB), ¿cuáles son las coordenadas del punto medio de CN? A) (–2; 4) C) (0; –1) B) (–4; 2) D) (0; 1) 15. Si en el gráfico: 3AP = 2AB, calcular (x + y). A) 6 B) 8 C) 6,5 D) 10 Javier Trigoso/Freddy Liñán B (7; 7) P (x; y) A (1; 1) Página 7