2 c) Proceso Adiabático Saturado - conveccion y microfisica de nubes

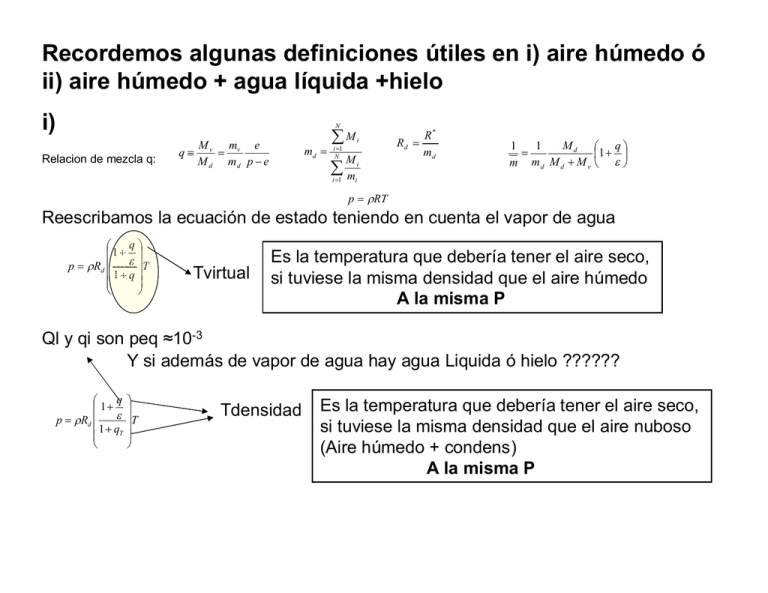
Recordemos algunas definiciones útiles en i) aire húmedo ó
ii) aire húmedo + agua líquida +hielo
i)
N
Relacion de mezcla q:
q
M
M v mv e

M d md p  e
md 
i 1
N
i
Mi
m
i 1
Rd 
R*
md
1
1
Md  q 

1  
m md M d  M v   
i
p  RT
Reescribamos la ecuación de estado teniendo en cuenta el vapor de agua
q

1 
 T
p  Rd 
1

q





Tvirtual
Es la temperatura que debería tener el aire seco,
si tuviese la misma densidad que el aire húmedo
A la misma P
Ql y qi son peq ≈10-3
Y si además de vapor de agua hay agua Liquida ó hielo ??????
q

 1

p  Rd 
 1  qT




T



Tdensidad
Es la temperatura que debería tener el aire seco,
si tuviese la misma densidad que el aire nuboso
(Aire húmedo + condens)
A la misma P
Procesos
en la
Atmosfera
Todos estos
1. Enfriamiento isobárico
procesos son
(δq≠0, dp=0, dh=δq)
2. Adiabaticos (δq =0,dp=0,dh=0)importantes en
las nubes!!!
3. Pseudoadiabáticos
Ejemplos caso (2) Procesos isoentálpicos:
1) Condens. ó Evaporización de agua en aire no saturado
Evaporación pp.
2) Mezcla horizontal de dos masas de aire.
3) Expansión Adiabática
1)
Enfriamiento Isobarico
Sistema cerrado q, w constantes, p constante , HR Varia
T↓
HR↑
y
es (T) ↓
Temperatura a la cual debe ser
Si e=es
T=Td
enfriado el aire hasta alcanzar a
saturación, con p constante.
Si la saturación se alcanza respecto al hielo la T es Tf, T de escarcha
2. Procesos Adiabaticos e Isobáricos
Sistema Cerrado, aire húmedo +agua, la ∆H=0(δq=0 y dp=0)
Escribimos la ecuación para la entalpía, para un estado inicial y final con Ti y otro Tf=Tiw
y wf=wsw
y …… …..llegamos a
Temperatura a la cual debe ser
lv
enfriado el aire por evaporación de
Tiw  T 
w ws
agua hasta que el mismo alcance
cpd
exactamente la saturación a p
constante y aislado
Y también de la misma forma estimamos


lv
Tie  T  w
cpd
Temperatura que alcanzaría el
aire húmedo si se secara
totalmente por condensacion del
vapor de agua y la misma sale del
sistema.
Presion
Liquido
Solido
Vapor
Relación entre las Temperaturas ya vistas
Td<Tiw<T<Tv<Tie
Temperaturq
2. Procesos Adiabaticos Isobaricos
Mezcla horizontal Isobárica
2 masas de aire humedo a la misma p
(T1,e1)
Si no existe condensacion,
H=m1h1+m2h2=0
Y reescribiendo y aproximando
m 1T 1  m 2 T 2
T 
m
m 1q1  m 2 q 2
q 
m
m 1 1  m 2  2
 
m
(T2,e2)
2. Procesos Adiabáticos:
Expansion Adiabática
Usamos : Teoría de la Parcela
Recordemos las Suposiciones
Realizadas
Te,P
– Parcela aislada del entorno. (ad)
– Cambios de Temperatura cumplen
Poisson.
– Equilibrio hidrostático, los
movimientos son suficientemente
lentos tal que es reversible)
Tp,P
w
Métodos para describir el proceso de
ascenso
Consideremos ahora que en esta parcela de
aire aislada los ASCENSOS puede ser de:
1) Aire seco
2) Contiene vapor de agua y cuando asciende
a) NO SATURA ó b) SATURA,
SATURA y el agua
permanece en la parcela
3) Idem 2b) pero el agua sale de la parcela y el
proceso se denomina pseudoadiabático
a)
b)
c)
d)
Proceso Adiabático Seco
Proceso Adiabatico Húmedo
Proceso Adiabático Saturado
Proceso Pseudoadiabático
2 a) Proceso Adiabático Seco
dq  c v dT  pd
dq  0
Parcela de Aire Seco
Te,P
Adiabático
Tp,P
w
c v dT  pd
Trabajo de expansión, resulta en
un cambio de T
Puedo usar ecuación de Poisson
 1000 
  T

 P 
Rd
c pd
Temperatura Potencial que se conserva
En un proceso adiabático seco
2. b) Proceso Adiabático Húmedo
• Tengamos en cuenta ahora un
proceso que sólo involucra al
vapor de agua y la parcela
permanece SUB-SATURADA.
q
mv
m
R
(m  mv )Rd  mvR v
m
2 b) Proceso Adiabático Húmedo
• Temperatura Potential para procesos de
ascenso que involucran aire húmedo que
“NO ALCANZA LA SATURACION”
 1000 

m  TI 
 PI 
(. 286 .07 q )
 1000 

 m   d 
 PI 
( .07 q )
POISSON
Se conserva para un proceso
adiabático húmedo que no
alcanza la saturación
2 c).Proceso Adiabático Saturado
• Calor Latente liberado ...
1. Calienta el aire
• Sistema Heterogéneo
– Aire Seco
– Vapor Agua
– Gotitas agua (material
condensado)
2. Parcela Realiza Trabajo
–
Calentamiento causa expansión
2 c) Proceso Adiabático Saturado
• Gotitas de agua
permanecen en la parcela.
• Calor Latente permanece
dentro de la parcela.
• Reversible
• ‘Adiabático’
• Isoentrópico
2 c.) Proceso Adiabático Saturado
• Masa del Sistema
– Air Seco (md)
• Constant
md
– Total de agua (mt)
• Vapor (mv)
• Agua Líquida (mw)
mt= mv + mw
2 c) Proceso Adiabático Saturado
• Condensación
– Vapor de Agua a Agua Líquida
dmv
Recordemos ………………
• 1) Condensación (Vapor agua a agua Líquida)
• 2) Evaporación (Agua líquida a vapor de agua)
Pierdo agua líquida y/ó vapor !!!!!
ó
Gano !!!!!!
dmw
dmv
2 c) Proceso Adiabático Saturado
lv dm v
dT
dp

 (m dc pd  m w c w )
 m dR d
T
T
p
• Ecuación para Proceso Adiabático Saturado
– Ignoramos calentamiento del Vapor de Agua
• Error es pequeñito
– Agua Líquida PERMANECE con la parcela que
asciende.
2 d.) Proceso Pseudoadiabático
• Agua líquida “cae fuera”
de la Parcela
• Calor Latente permanece
dentro de la Parcela
• Calor Latente calienta
“SOLO” el aire seco.
2 d.) Proceso Pseudoadiabático
• Irreversible
• Pseudoadiabatico
• Cambios en la Entropía
2 d.) Proceso Pseudoadiabático
• Qué hacemos en nuestra ecuación de dS?
– Tengamos en cuenta que no hay masa de agua
para calentar!
lv dm v
dT
dp

 m dc p d
 mdR d
T
T
p
 1000
 e   d 
 PI



0 . 285 (1  . 28 w )
Podemos Usar la aprox. de
Bolton para definir Θe

 3376

exp  w (1  0 . 81 w ) 
 2 . 54  
 Tlcl
 

Temperatura Potencial
equivalente (e )
• ‘es conservada’ para
– Proceso Adiabatico seco
– Proceso Pseudoadiabatico
e
constante
Energía Potencial Disponible
Convective Available Potential Energy
CAPE
pi
CAPEi= R
 Td ln p
donde
T = Tparcela  Tentorno
Pniveequi
Proceso pseudoadiabatico
Agua sale sistema!!!
q

 1

Tv  T 
 1  qT








q

 1

T  T 
 1  qT








Proceso Reversible, existen 2 efectos opuestos, carga hidrometeoros y contenido
agua:
1. Peso condensado tiende a enfriar (domina hasta trop media)
2. Cantidad aumenta el calentamiento
TVPparcelaTventorno Tpad Tventorno
Tparc .rev  Tventorno T p  a  Tventorno
Domina en niveles superiores
Domina en niveles bajos y medios
Sondeo esquemático que muestra el proceso con y
sin corrección para la Tv
SIS 20/9/03
Comparación
Reversible
Pseudo-adia
¿Cómo es ∆T?
Comparacion
Reversible
Pseudo-adia
Acá miramos ∆Tseco