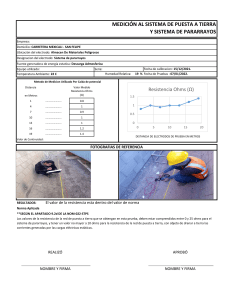
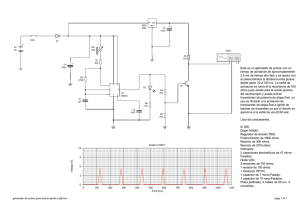
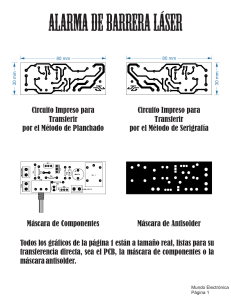
Instituto Politécnico Nacional UPIITA Segundo examen ordinario de Matemáticas I Nombre:___________________________ Boleta:

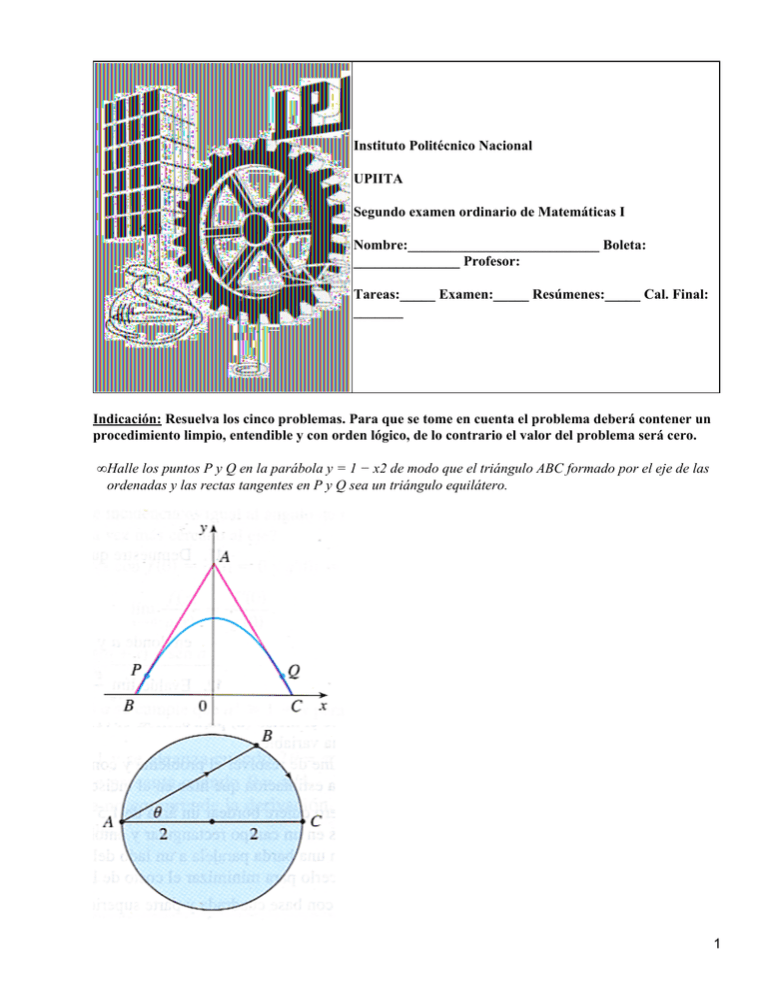
Instituto Politécnico Nacional
UPIITA
Segundo examen ordinario de Matemáticas I
Nombre:___________________________ Boleta:
_______________ Profesor:
Tareas:_____ Examen:_____ Resúmenes:_____ Cal. Final:
_______
Indicación: Resuelva los cinco problemas. Para que se tome en cuenta el problema deberá contener un
procedimiento limpio, entendible y con orden lógico, de lo contrario el valor del problema será cero.
• Halle los puntos P y Q en la parábola y = 1 − x2 de modo que el triángulo ABC formado por el eje de las
ordenadas y las rectas tangentes en P y Q sea un triángulo equilátero.
1
• Una mujer que se encuentra en un punto A sobre la playa de un lago circular con radio de 2km desea
llegar al punto C, opuesto al A sobre el otro lado del lago, en el tiempo más corto posible. Puede caminar
a razón de 4km/h y remar en un bote a 2km/h. ¿En qué ángulo en relación con el diámetro debe remar?
• (a) Halle asíntotas verticales y horizontales, (b) Intervalos de crecimiento y decrecimiento, (c) máximos y
mínimos locales, (d) intervalos de concavidad y puntos de inflexión, y (e) graficar la función:
• Un recipiente en forma de cono invertido tiene una altura de 16cm y un radio de 5cm en la parte superior.
Está parcialmente lleno con un líquido que exuda a través de los lados con una razón proporcional al área
del recipiente que está en contacto con el líquido. (El área superficial de un cono es ð r l, donde r es el
radio y l es el apotema). Si vertemos líquido en el recipiente a razón de 2cm3/min., la altura del líquido
disminuye a razón de 0.3cm/min., cuando esa altura es de 10cm. Si nuestro propósito es mantener el
líquido a una altura constante de 10cm, ¿con qué rapidez debemos verter el líquido en el recipiente?
• Calcular:
sin usar calculadora. Sin procedimiento el resultado es incorrecto.
Pag. 257−258
20, 29.
Pag. 335−336
22, 27.
PROBLEMA 20
Una alberca mide 20 pies de ancho, 40 de longitud, 3 de fondo en la parte baja y 9 pies en la parte honda.( En
la figura que sigue se ilustra una sección longitudinal.) Si se llena con un flujo de 0.8pies cubicos por
minuto¿Con que velocidad sube el nivel de agua cuando la profundidad, respecto a la parte honda, alcaza 5
pies ?
2
PROBLEMA 22
SIN ESQUEMA
Una cometa a 100 pies del suelo se mueve horizontalmente con una velocidad de 8 pies sobre segundo ¿ Con
qué velocidad cambia el angulo formado por el hilo y la horizontal, cuando se han soltado 200 pies de cuerda?
PROBLEMA 27
Si dos resistores R1 y R2 estan conectados en paralelo, como en la figura, entonces la resistencia total R,
medida en Ohms esta dada por
1/R = 1/R1 + 1/R2
Si R1 y R2 crecen a razón de 0.3 ohms por segundo y 0.2 ohms por segundo, respectivamente, ¿ con que
rapidez cambia R en el instante en que R1= 80 ohms y R2 = 100 ohms?
3
PROBLEMA 29
Una escalera de 10 pies de longitud se apoya en un muro vertical. Si su extremo inferior se desliza alejándose
de la pared con una velocidad de 2 pies por segundo ¿ Con qué velocidad cambia el àngulo formado entre la
parte superior de la escalera y el muro cuando ese ángulo mide pi/4 radianes?
SIN ESQUEMA
4