la curva normal - Bioestadistica
Anuncio

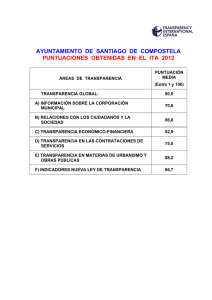
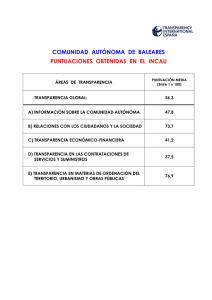
Métodos de Investigación en Educación Tema 7 TEMA 7 EL MODELO DE LA CURVA NORMAL. CONCEPTO Y APLICACIONES 1. Puntuaciones diferenciales y puntuaciones típicas Pág. 96 2. La curva normal Pág. 97 3. Cálculo de áreas bajo la curva normal Pág. 98 3.1. Caso 1: Cálculo del número de individuos que quedan por encima y por debajo de una puntuación directa Pág. 98 3.2. Caso 2: Cálculo del número de individuos comprendidos entre dos puntuaciones directas Pág. 99 3.3. Caso 3: Cálculo de una puntuación directa a partir de un área determinada Pág. 100 3.4. Caso 4: Cálculo de las puntuaciones directas que comprenden un área determinada Pág. 101 3.5. Caso 5: Cálculo del área comprendía por encima y por debajo de una puntuación directa Pág. 102 3.6. Caso 6: Cálculo de un área comprendida entre dos puntuaciones directas Pág. 102 4. Introducción a las medidas individuales: asimetría y curtosis Pág. 103 Anexo 1: Áreas bajo la curva normal Pág. 105 95 Métodos de Investigación en Educación Tema 7 Las puntuaciones obtenidas al medir una característica con el instrumento de medida adecuado e denominan puntuaciones directas. Los cálculos efectuados hasta ahora en los temas anteriores han sido realizados con estas puntuaciones. Sin embargo, en ocasiones trabajar únicamente con estas puntuaciones puede ser insuficiente. Imaginemos un estudiante que ha obtenido una puntuación de 116 puntos en una determinada prueba de hábitos de estudio. Para poder extraer conclusiones acerca de la bondad de sus hábitos de estudio hay que conocer la escala en la que está medida, las puntuaciones máxima y mínima posibles, el índice de dificultad de la prueba o la puntuación media de la población de referencia, es decir, cual es la puntuación media esperada del alumnado con los que puede comparar a este estudiantes cuyos hábitos de estudio se pretenden analizar. Si la media del colectivo de referencia es de 100 podemos afirmar que nuestro alumno está por encima, pero si la media del colectivo es de 200, la conclusión sería diferente. Esta situación se resolverá efectuando transformaciones con la puntuación directa que este estudiantes ha obtenido en la prueba. 1. Puntuaciones diferenciales y puntuaciones típicas Las puntuaciones directas son difíciles de interpretar, por ello es conveniente relacionar la desviación de un sujeto respecto de la Χ con una medida que nos diga la posición del mismo con respecto al resto de los sujetos. Es decir, se trata de relacionar la desviación de un sujeto con la desviación de todo el grupo. Para ello utilizaremos la puntuación típica o desviación “z”. Estas puntuaciones permiten expresar la diferencia que existe entre la puntuación directa y la media, tomando como unidad la desviación típica de la variable. De este modo, todas las puntuaciones son reducidas a una única unidad de medida (con media igual a cero), siendo posible comparar valores que corresponden a diferentes variables y/o colectivos. Para calcular la puntuación típica utilizaremos la siguiente fórmula: z= Χ−Χ x = s s 96 Métodos de Investigación en Educación Tema 7 El numerador de la fórmula aquí presentada se corresponde con las denominadas puntuaciones diferenciales (x), es decir, las que se obtienen al calcular la diferencia de la puntuación de cada elemento con respecto de la media del grupo de referencia. Indicará si el elemento obtiene en dicha variable una puntuación mayor, mejor o igual que la media del colectivo del que forma parte. 2. La curva normal La curva normal o campana de Gauss se concibe como un histograma donde el número de intervalos aumenta de forma indefinida, disminuyendo progresivamente su amplitud. Tiene muchas y muy importantes propiedades, como, por ejemplo: • La altura máxima la alcanza en el punto central, cuyo valor (valor máximo) se sitúa en la media de la distribución. • La curva es simétrica con respecto al eje vertical que pasa por la media. • En cualquier distribución normal, la media, la moda y la mediana tienen el mismo valor. 5 4 3 2 1 0 -3 -2 -1 0 1 2 3 Dependiendo de la media y de la desviación típica existen infinitas curvas normales pero todas ellas equivalentes. Sin embargo, la distribución con la que habitualmente se trabaja en la normal típica, es aquella que tiene de media 0 y de desviación típica 1. 97 Métodos de Investigación en Educación Tema 7 3. Cálculo de áreas bajo la curva normal La curva normal representa un histograma en el que el intervalo es infinitamente pequeño. Al igual que en el histograma, para averiguar la proporción de elementos que obtienen puntaciones inferiores o superiores a una dada, bastará con saber la proporción del área de la parte referida. Cuando utilizamos “z” hacemos comparables todas las puntuaciones. Cuando tenemos una “z” sabemos el área que ocupa expresada en porcentajes. Para ello, hay que buscar el valor de “z” en la tabla anexa (áreas bajo la curva normal). Para su cálculo, en todos los casos los casos que se ilustran a continuación, seguiremos el siguiente proceso: 1º Dibujar la curva con una distribución normal. 2º Representar los datos que tenemos en la curva normal. 3º Calcular la puntuación típica “z”. 4º Establecer el valor del porcentaje de “z”, en la tabla anexa. 3.1. Caso 1: Cálculo del número de individuos que quedan por encima y por debajo de una puntuación directa Dado un test que nos ofrece una Media de 50 y una Desviación típica de 6 y suponiendo que la muestra se distribuye normalmente, debemos averiguar las frecuencias en % por encima y por debajo del valor X1= 60. ¿Cuál es el número de individuos en % que quedan por encima y por debajo de la puntuación? 98 Métodos de Investigación en Educación Tema 7 X 1= 6 50 X = 50 1,6 Hallamos el valor Z asociado a la puntuación directa según la fórmula de cálculo: X −X z= 1 s = 6 - 6 = 1,67 Buscamos esa Z en la tabla anexa y localizamos el área: 1,67 0,4525 que en % es igual a 45,25% de los individuos. Es el número de sujetos que hay entre la Χ y la Z=1,67. (la parte rayada). Si al 45,25% de los casos le sumamos el 50% obtenemos el 95,25%, deduciendo que la puntuación obtenida por el sujeto se encuentra por encima del 95,25% de los casos y por debajo del 4,75% (100%-95,25%). 3.2. Caso 2: Cálculo del número de individuos comprendidos entre dos puntuaciones directas Teniendo en cuenta los siguientes datos: Media=50, Desviación Típica=6, X1=45, X2=35, averiguar el porcentaje de individuos que tienen puntuaciones comprendidas entre X1 y X2. X 1= 4 X 2= 35 -2.5 -0.8 X = 50 99 Métodos de Investigación en Educación Tema 7 Hallamos los valores Z asociados a cada puntuación directa según la fórmula de cálculo y buscamos las áreas asociadas en la tabla pertinente: z = X 1− X 1 s = z = X 2− X 2 s = -5 6 -15 6 = - 0. 83 29,67% = - 2. 5 49,38% Para calcular el número de sujetos entre las dos puntuaciones hay que restar los dos porcentajes obtenidos: 49,38% - 29,67% = 19, 71 % 3.3. Caso 3: Cálculo de una puntuación directa a partir de un área determinada ¿Cuál es la puntuación que deja por debajo el 75 % de los casos teniendo en cuenta los siguientes datos: Media=59, Desviación típica: 6? 75% X = 50 Como el 75% de los casos no se puede buscar en la tabla de las áreas, buscamos el 25% (dado que son valores simétricos) que, aproximadamente, es 24,86. Esto es igual a Z=0,67. Despejando: 0,67 = X 1− 5 6 100 Métodos de Investigación en Educación Tema 7 X1 - 50 = 0,67 (6) X1 - 50 = 4,02 X1= 4,02 + 50 = 54,02 3.4. Caso 4: Cálculo de las puntuaciones directas que comprenden un área determinada Averiguar las puntuaciones que hay que obtener a ambos lados de la media para que el área comprendida entre ambos puntos, contenga al 50% de los casos, sabiendo que la Media es 50 y la Desviación Típica 6. 25 % 25 % X = 50 Buscamos el 25% en la tabla de áreas bajo la curva normal que, aproximadamente, es 24,86 %, cuyo valor asociado de Z es 0,67. Despejando en la fórmula de cálculo de las puntuaciones Z obtendremos las puntuaciones directas: X1 - 50 = 0,67 (6) X1 - 50 = 4,02 X1= 4,02 + 50 = 54,02 por encima --------------------X2 - 50 = - 0,67 (6) X2 - 50 = - 4,02 X2= - 4,02 + 50 = 45,98 por debajo 101 Métodos de Investigación en Educación Tema 7 3.5. Caso 5: Cálculo del área comprendía por encima y por debajo de una puntuación directa Hallar la probabilidad en porcentaje (%) de que un valor escogido al azar sea inferior a X1= 60, conociendo los siguientes datos: Media=50, Desviación típica=6. 45,25% X 1 = 60 50 X = 50 −5 z = 60 6 = 1,67 45,25 % La probabilidad es: 50% + 45,25% = 95,25% 3.6. Caso 6: Cálculo de un área comprendida entre dos puntuaciones directas Hallar la probabilidad en porcentaje (%) de que un individuo escogido al azar obtenga una puntuación comprendida entre X1 y X2, teniendo en cuenta los siguientes datos: Media=50, Desviación típica=6, X1=39 y X2=62. - 1,83 X = 50 2 102 Métodos de Investigación en Educación Tema 7 Hallamos z: z = 39 − 50 1 s = -11 6 12 z = 62 − 50 = 2 s 6 = - 1.83 46,64% = 2 47,72% Para calcular el número de sujetos entre las dos puntuaciones hay que: 46,64% + 47,72% = 94,36 % 4. Introducción a las medidas de forma: asimetría y curtosis Además de las medidas de tendencia central y dispersión, se utilizan otros dos tipos de medidas que nos ayudarán a describir mejor las variables: la asimetría y la curtosis. El índice de asimetría representa el grado en el que los datos de una distribución de frecuencias se reparten por encima y por debajo de la tendencia central. La distribución normal es simétrica y tiene un valor de asimetría igual a 0. Una distribución que tenga una asimetría positiva significativa tiene una cola derecha larga. Una distribución que tenga una asimetría negativa significativa tiene una cola izquierda larga. Como regla aproximada, un valor de la asimetría mayor que el doble de su error típico se asume que indica una desviación de la simetría. 103 Métodos de Investigación en Educación Tema 7 El índice de curtosis representa el grado de apuntamiento de una distribución de frecuencias. Para una distribución normal, el valor del estadístico de curtosis es 0 y diremos que ésta es mesocúrtica. Una curtosis positiva indica que las observaciones se concentran más y presentan colas más largas que las de una distribución normal, así como su apuntamiento; se trata de una distribución leptocúrtica. Una curtosis negativa indica que las observaciones se agrupan menos y presentan colas más cortas, siendo la distribución platicúrtica. 104 Métodos de Investigación en Educación Tema 7 Anexo 1: Áreas bajo la curva normal 105