MOMENTO DE UA FUERZA
Anuncio

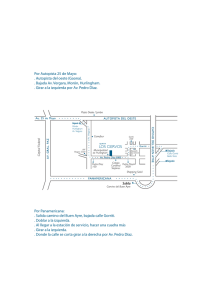
MOMENTO DE UNA FUERZA. FORMULACIÓN ESCALAR Cuando una fuerza se aplica a un cuerpo, ésta producirá una tendencia a que el cuerpo gire alrededor de un punto que no está en la línea de acción de la fuerza. Esta tendencia a girar se conoce en ocasiones como par de torsión, pero con mayor frecuencia se denomina el momento de una fuerza o simplemente el momento. Por ejemplo, considere la llave de torsión para hacer girar el tubo: La fuerza F tenderá a hacer girar el tubo alrededor del eje z La fuerza no hará girar al tubo alrededor del eje z, tiende a girarlo alrededor del eje x. Si bien no es posible girar al tubo de esa forma, de todos modos crea la tendencia a la rotación y por lo tanto se produce el momento. La fuerza aplicada no produce momento respecto a O, ya que la línea de acción de la fuerza pasa por O y por tanto no es posible la tendencia a la rotación. CUANTO MAYOR SEA LA FUERZA O LA DISTANCIA TANTO MAYOR SERÁ EL EFECTO 1 El momento Mo con respecto al punto O ó con respecto a un eje que pase por O y sea perpendicular al plano es una cantidad vectorial puesto que tiene magnitud, dirección y sentido específicas Mgnitud : MO = F d Donde d es la distancia perpendicular desde el eje en el punto O hasta la línea de acción de la fuerza. La dirección está definida por su eje de momento, el cual es perpendicular al plano que contiene la fuerza F y por su brazo de momento d. Para establecer el sentido de dirección se utiliza la regla de la mano derecha. Momento resultante. Puede determinarse al encontrar la suma algebraica de los momentos causados por todas las fuerzas en el sistema Como convención, se considera de manera general los momentos positivos en sentido antihorario y negativos en sentido horario. 2