Descargar

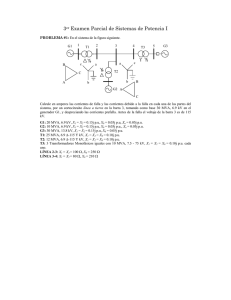
Facultad de Ingeniería (U.N.M.D.P.) - Dpto. de Ingeniería Eléctrica - Area Electrotecnia - Electrotecnia 3
GUÍA DE PROBLEMAS Nº 1
Tema: El método por unidad
PROBLEMA Nº 1: En un sistema eléctrico se tienen las siguiente tensiones: 108, 120 y 126
KV. Si se adopta como tensión base Ub =120 [kV]. ¿Cuál es el valor por unidad [p.u] de las
tensiones dadas?
Rta: Valores pu: 0,9; 1; 1,05
PROBLEMA Nº 2: Ídem al PROBLEMA Nº 1, pero para los tres valores de potencia: 250
MVA, 2 MVA y 4 MVA, adoptando como valor base Sb = 2 MVA.
Rta: Valores p.u.: 125; 1; 2
PROBLEMA Nº 3: Para los siguientes casos, calcular los valores correspondientes a la
corriente e impedancia base: a) Sb= 2 MVA; Ub= 138 kV; b) Sb= 5 MVA, 220 kV.
Rta: a) 14,5 A y 9,52  ; b) 22,73 A y 9,7 
PROBLEMA Nº 4: Tomando como impedancia base “Zb” los valores calculados en el
PROBLEMA Nº3, determinar el valor en Ohms de las siguientes impedancias, cuyos valores
por unidad son: Za= 0,25, Zb= 0,85 y Zc= 1,1.
Rta: a) Con Zb = 9,52 k: Za = 2.380  , Zb = 8.092  , ZC = 10.472 
b) Con Zb = 9,7 k: Za = 2.425  , Zb = 8.245  , ZC = 10.670 
PROBLEMA Nº 5: La reactancia X” de un generador es 0,20 por unidad basada en la placa
del generador de 13,2 kV y 30.000 kVA. La base para los cálculos es 13,8 kV y 50.000 kVA.
Encuentre X” en esta nueva base.
Rta: X” = 0,306 pu
PROBLEMA Nº 6: Un transformador monofásico se especifica como 110/ 440 V y 2,5 kVA.
La reactancia de pérdidas medida desde el lado de baja tensión es 0,06. Determinar la
reactancia de pérdidas por unidad. ¿Que conclusión extrae?
(Téngase en cuenta que la relación de transformación se define como r = U1/U2 y que se
cumple que U1.I1 = U2. I2)
Rta: XT pu = 0,0124.
PROBLEMA Nº 7: Para el sistema de potencia de la figura compuesto de dos
transformadores T1 y T2 unidos por una línea inductiva, se desea determinar la impedancia
en por unidad del conjunto. Despreciar las resistencias de los elementos constitutivos del
sistema.
Rta: XTOTAL = 0,176 pu
1
Facultad de Ingeniería (U.N.M.D.P.) - Dpto. de Ingeniería Eléctrica - Area Electrotecnia - Electrotecnia 3
PROBLEMA Nº 8: Para el sistema de potencia de la figura, compuesto por dos
transformadores en paralelo, una línea y un transformador, según la figura, calcular la
impedancia en por unidad de cada elemento y la total, siendo que la tensión en el punto M
es la nominal más 2,5%.
Rta: Tomando Sb = 10 MVA y UpuntoM = 133,25 kV: XT1= 0,0952; XT21= 0,156; XT22 = 0,104;
XL = 0,106; Xtotal = 0,2636 pu
PROBLEMA Nº 9: Hallar el circuito
equivalente en valores por unidad del circuito
trifásico dado en la figura, tomando como base
la potencia y tensión en el generador. Datos:
Generador: 30 MVA ; 13,8 kV ; Xg = 20%
Transformadores: 35 MVA ; 13,2 / 115 kV ; ucc
= 10 %
Línea: XL = 80 
Motores: M1: 20 MVA ; 12,5 kV ; Xm1 = 20 %; M2: 10 MVA ; 12,5 kV ; Xm1 = 20 %
Rta: El diagrama de reactancias estará constituido por las siguientes reactancias en
pu referidas a los valores base del generador: XG = 0,20; XT1= 0,078; XT2= 0,078; XL =
0,167; XM1 = 0,246; XM1 = 0,492.
PROBLEMA Nº 10: Un transformador de 50 MVA y 34,5/161 kV, con una reactancia de
dispersión del 10% está conectado a un sistema de potencia donde todas las impedancias
están tomadas sobre los valores base 100 MVA y 34,5 kV o 161 kV. Obtenga el valor en por
unidad del transformador para las bases del sistema.
Rta: XT = 0,20
PROBLEMA Nº 11: Un generador y un banco de
transformadores conectados como indica la figura.
Encontrar el valor de la impedancia del conjunto,
en por unidad, adoptando como bases 100 MVA y
110 kV. El banco de transformadores está
operando a una tensión nominal de 3,9 kV del lado
de baja tensión.
Rta: XTotal = 1,5143
PROBLEMA Nº 12: Un
generador trifásico de 30.000
kVA y 13,8 kV tiene una
reactancia subtransitoria del
15%. El generador alimenta
a dos motores a través de
una línea de transporte, con
transformadores en ambos
extremos, tal como se representa en el diagrama unifilar de la figura. Los motores tienen
como entradas nominales 20.000 y 10.000 kVA, ambos a 12,5 kV, con X”m= 20%.
2
Facultad de Ingeniería (U.N.M.D.P.) - Dpto. de Ingeniería Eléctrica - Area Electrotecnia - Electrotecnia 3
El transformador trifásico T1 tiene como valores nominales 35.000 kVA – 13,2 () – 115 ()
kV, con reactancia de dispersión del 10%. El transformador T2 está compuesto de tres
transformadores monofásicos, cada uno especificado como 10.000 kVA, 12,5 – 67 kV, con
reactancia de dispersión del 10%. La reactancia en serie de la línea de transmisión es 80 .
Dibuje el diagrama de reactancias con todas las reactancias indicadas por unidad. Elija la
especificación del generador como valores base.
Rta: Las reactancias en pu, referidos a Sb = 30 MVA y UB = 13,8 kV, valen:
XG1 = j 0,15 ; XT1= j 0,0784; XT2= j 0,094; Xlinea = j 0,167; Xm1 = j 0,282; Xm1 = j 0,563
PROBLEMA Nº 13: Si los motores del problema anterior tienen entradas de 16.000 y 8.000
kW, respectivamente, a 12,5 kV y ambos operan con un factor de potencia unitario,
encuentre la tensión en los terminales del generador.
Rta: Vgenerador = 1,009 16,1º pu, Vgenerador = 13,92 kV (tensión de línea)
PROBLEMA Nº 14: Dado el sistema de transmisión de la figura, determinar utilizando
valores por unidad las corrientes y tensiones en los distintos puntos del sistema cuando la
tensión en la barra “C” es de 6,6 kV y la carga tomada por el motor asincrónico es de 10
MVA, con factor de potencia igual a 1.
Datos:
GENERADOR [G1]
Sg = 10 MVA; Ug = 6,6 kV; Xd = 100 %
TRANSFORMADORES:
[T1]: 10 MVA; 6,6 / 13,2 kV; Xt = 5 %
[T2]: 30 MVA; 13,2 / 115 kV; Xt = 7 %
[T3]: 25 MVA; 110 / 6,9 kV; Xt = 8 %
LINEAS:
[L1]: r= 0,08 / km; xl= 0,51 / km; long= 10 km.
[L1]: r= 0,15 / km; xl= 0,64 / km; long= 50 km.
MOTOR:
30 MVA; 6,6 kV; xM = 75%
CARGA:
10 MVA; fp = 0,7 (L)
T2
L2
T3
Ba
B0
G1
L1
B1
B2
Carga C
T1
Bb
M
Bc
B = barras de referencia
Rta: El diagrama de reactancias estará constituido por las siguientes reactancias en
pu, referidos a Sb = 20 MVA y UBarra C = 6,6 kV
XG1 = j 2,42 ; XT1= j 0,121; XT2= j 0,057; XT3 = j 0,07; XL1 = j 0,71; RL1 = 0,11; XL2 = j 0,058 ;
RL2 = 0,014. Las corrientes serán: Icarga = 0,5 -45º, Imotor = 0,5 0º, Itotal = 0,92 -22,4º.
Las tensiones valdrán: UC = 1 0º , Ubarra B2 = 1,027  3,35º, Ubarra B = 1,088  8,08º,
Ubarra Ba = 1,58  27,15º, Ubarra B0 = 1,67  29,63º. La corriente I = 0,92 - 22,4º
PROBLEMA Nº 15: Dado el circuito trifásico de la figura, hallar su equivalente en v.p.u.
Calcular en por unidad y en magnitudes eléctricas, las potencias, tensiones y corrientes en
todas las barras y elementos.
Datos: P + j Q = 2 + j 2,67 [MVA]; j QC = - j 1,17 [MVAr]
T2 = transformador real: S = 3 MVA, 132/13,2 kV, uCC = 5 %
T1 = transformador real: S = 4 MVA, 132/13,2 kV, uCC = 6 %
L1 = linea monofásica; l = 100 km; r = 0,2 /km ; x = 0,39 /km
3
Facultad de Ingeniería (U.N.M.D.P.) - Dpto. de Ingeniería Eléctrica - Area Electrotecnia - Electrotecnia 3
L2 = linea monofásica; l = 120 km; r = 0,1 /km ; x = 0,40 /km
U4 = 13,2 0º [kV]
Rta: Las tensiones en pu valen: U4 = 1  0º, U3 = 1,0255  1,87º, U2 = 1,0286  1,97º, U1
= 1,0525  3,54º. La corriente I = 0,25 - 36,87º
PROBLEMA Nº 16: Establecer el circuito
equivalente monofásico en v.p.u. del sistema
dado en la figura, referido a una base de potencia
de 100 MVA y a una base de tensión de 385 kV,
siendo ambos valores trifásicos.
Representar a la línea como un circuito serie de
resistencia y reactancia.
Datos:
G1 = G2 = generadores de 170 MVA; Tensión de generación Ug = 13,8 kV
T1 = T2 = transformadores trifásicos 390/13,2 kV; 180 MVA; uCC = 10 %
L1 = línea de transmisión de 380 kV, longitud l = 320 km; r = 0,0298 /km; X = 0,338 /km.
Si la carga trifásica conectada al final de la línea es de S = 290 + j 99 MVA y la tensión al
final de la línea es de 380 kV, calcular:
a) La tensión al neutro y la corriente en por unidad al principio de la línea.
b) La tensión al neutro, la corriente y la potencia compleja por fase en por unidad, del
lado de baja tensión de cada transformador.
c) La tensión entre conductores, la potencia compleja trifásica de cada transformador.
Rta: a) Uprincipio línea = 1,099  10,91º , Ilinea = 3,105  - 18,85º
b)UBT trafo1 = 1,146 14,81º , IBT trafo1 = 1,5525  - 18,85º , Strafo1 = 1,78  33,66º
c)Ulinea BT trafo1 = 14,9 KV , Strafo1 = 178 MVA
PROBLEMA Nº 17: El
sistema trifásico de la figura
consta de los siguientes
elementos:
Generador G1: 100 MVA, 15
kV, Xsg1= 0,15 p.u
Generador G2: 80 MVA, 15
kV, Xsg2= 0,15 p.u
Línea L1 y L3 impedancia 10 + j 50 W/fase
Línea L2 y L4 impedancia 20 + j 60 W/fase
Transformador T1: 80 MVA, 15/165 kV, XCCT1=0,1 p.u
Transformador T2: 60 MVA, 165/12 kV, XCCT2=0,1 p.u
Carga M1: a potencia constante de 50 MVA a 165 kV y fdp=0,8 inductivo
Carga C2: de impedancia constante, 40 MVA a 165 kV y fdp = 0,95 capacitivo
Interruptores S1, S2, S3 y S4 de impedancia despreciable.
a) Dibujar el esquema del sistema, por fase, indicando los valores de las impedancias en
valores por unidad, tomando como base 100 MVA y 15 kV.
4
Facultad de Ingeniería (U.N.M.D.P.) - Dpto. de Ingeniería Eléctrica - Area Electrotecnia - Electrotecnia 3
b) Con los interruptores S1 y S3 cerrados y S2 y S4 abiertos, determinar la tensión y
corriente en la carga C2 y en el generador G1, en valores por unidad y valores reales, para
mantener la carga M1 a una tensión de 165 0º kV.
c) Con los interruptores S3 y S4 cerrados y S1 y S2 abiertos, determinar la tensión y la
corriente en el generador G1, en valores por unidad y valores reales, para mantener la
carga C2 a una tensión de 165  0º kV, con el generador G2 a tensión de 13 +5º kV.
Rta:
b) Uc2 = 1,023-1°pu; Uc2 = 168,9- 1°KV; UG1 = 1,103- 8,4° pu; UG1 = 16,5- 8,4° KV
c) iG1 = 0,3 69,3° pu ; iG1 = 1155 69,3° A KV ; UG1 = 1,026 5° pu ; UG1 = 15,45° KV
PROBLEMA Nº 18: En el diagrama de la figura, la tensión del generador (nudo1), se eleva
mediante dos transformadores trifásicos idénticos en paralelo, T1 y T2, a 230 kV (nudo 2),
que alimentan a una carga y a una línea de 50 km que termina en otro transformador T3 a
cuya salida se conecta un motor a 69 kV.
Las características nominales de los diversos elementos del sistema son:
Generador 100 MVA, 15 kV, Xsg= 0,1 p.u
T1 y T2 50 MVA, Y- , 15/230 kV, Xcc= 0,2 p.u
T3 70 MVA,  -Y, 230/69 kV, Xcc= 0,1 p.u
Z de línea (2-3) XL = j 6 O/fase
Carga (Z constante) 20 MW, 230 kV
Motor (P constante) 50 MVA, 69 kV, f.d.p 0,8 inductivo
Tomando como base los valores nominales del generador y suponiendo que en la situación
considerada el valor medido de la tensión en bornes del motor es de 69 kV, determinar en
módulo y argumento:
a) La corriente en el motor y la tensión, corriente y potencia en la carga.
b) La tensión, corriente y potencia desarrollada por el generador
c) La tensión y corriente en la línea del primario del transformador T3.
Rta: a) Imotor = 0,5  - 36,87°, Imotor = 418,35 - 36,87° A; Ucarga = 1,0478 3,37° , Ucarga =
241 - 26,63° KV, Icarga = 0,21  3,37°, Icarga = 52,7 - 26,63° A, Scarga = 0,22 pu; Scarga = 22
MW.
b) IG = 0,675  - 25,3º, IG = 2592  - 25,3º, UG = 1,119  9,46º, UG = 16,8 9,46º, SG =
0,755 34,76º, SG = 75,5  34,76º
c) U3 = 1,0445  3,14º, U3 = 240,2  3,14º KV; I3 = Im = 0,5  - 36,87º , Im = 125,5  36,87º A.
Glf/2015
5