La Lección de Hoy es sobre Líneas Perpendiculares y
Anuncio

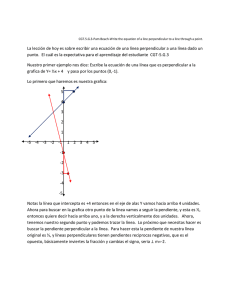
LF.3.A1.7-Tara Walker-Parallel and Perpendicular Lines- La Lección de Hoy es sobre Líneas Perpendiculares y Paralelas. El cuál es la expectativa para el aprendizaje del estudiante del estudiante LF.3.A1.7 ¿Que son las Líneas Paralelas? Son dos distintas líneas coplanarias que no interceptan. Nota, las líneas paralelas tienen las mismas pendientes. Gráficamente lo que queremos decir es, es que estas dos líneas azules notaras que están marcadas por una distancia que las separa en rojo. Y no importa donde vallan en estas líneas siempre será la misma distancia, y sus pendientes serán las mismas. Ahora que sabemos estos vamos a buscar la ecuación de la línea que contiene el punto (2,3) y esta paralela a la línea y= 2x +5, en el momento que lees este realizaras que tiene la misma pendiente. Entonces la pendiente de la línea que nos han dado la y= 2x +5 y la línea que estamos buscando tendrán la misma pendiente. Ahora para definir una ecuación de cualquiera línea necesitas un punto que ya lo tenemos es (2,3) y necesitamos la pendiente. ¿Cómo encontramos la pendiente? Mira la línea que es paralela y= 2x +5 , notas que está en la forma de forma y= mx +b o sea, la m, que es la pendiente es el coeficiente de X, que en este caso es 2. Entonces la nuestra pendiente es m =2. Recuerda, m es la pendiente de la línea. Ahora tenemos un punto, y pendiente, vamos a escribir la ecuación. La ecuación que siempre usamos es y-y1 = m(x-x1). Ahora, x1 – y1 es nuestro orden de pares, o sea nuestro punto. Recuerda en el orden de pares “ x” es primero, “Y” es segundo, y “m” es nuestra pendiente. Si sustituimos nuestros valores tendremos Y-3 = 2(x-2) Ahora, en cada ecuación de una línea, usualmente resolvemos por “Y”, porque es fácil para graficar. Ahora, ¿Cómo resolveremos esta ecuación por “Y”? Para hacer esta y= ms +b vemos que la ecuación no tiene paréntesis entonces necesitamos eliminar el paréntesis. Vamos a distribuir el dos. O sea multiplicamos todo en el paréntesis. Tenemos: Y-3 = 2x -4 El próximo paso para resolver por Y, es cancelar el -3, para hacer esto tenemos que hacer lo opuesto, que es sumar tres en los dos lados. Y-3 +3 = 2x -4 +3 El -3 y el +3 se cancelan, y tenemos Y=3 , y combinamos los dos términos a la derecha Y= 2x -4 +3 que seria -1, la ecuación seria y= 2x -1 Y esta es la ecuación de la línea que es paralela. ¿Cómo podemos probar esta? Vamos a usar una grafica primero. Pero, ¿Cómo graficaremos una línea? Siempre empieza con la Y que intercepta, que es el numero al final de la ecuación que es +5, que quiere decir en la Y desde el origen, voy hacia arriba 5 unidades. Ahora para el segundo punto en la línea necesitamos seguir la pendiente, y la pendiente de la línea es 2, y para recordarte la pendiente es el aumento sobre la base, o el cambio en Y, sobre el cambio en X. Recuerda se sobre entiende que dos está sobre uno, quiere decir desde el primer punto que es (0,5) para tener un segundo punto en la línea necesitamos seguir la pendiente, ir dos unidades hacia arriba, y uno a la derecha, porque el valor es positivo. Si voy hacia arriba uno a la derecha, y dos hacia arriba tengo mi segundo punto. Ahora que tengo 2 puntos trazo una línea sobre estos dos puntos. Aquí esta nuestra línea en rojo. Ahora, haremos la segunda, esta vez usaremos verde para diferenciarlas. De nuevo, sigue los mismos pasos. Sustituye tú Y que intercepta, que es el negativo. Ahora, el negativo quiere decir desde el origen iremos hacia abajo una unidad, y seguimos la pendiente y notaras que la pendiente es la misma, 2, quiere decir que desde el -1 vas hacia arriba dos unidades y a la derecha una para tu segundo punto. Ahora, traza una línea en verde, notas algo con respecto a estas líneas. Tienen las mismas distancias que las separan. Notaras algo con respecto a estas líneas. Tienen las mismas distancias que las separan. Ahora, sabemos son líneas paralela. No tienen un punto en común. Ahora que hablamos de líneas paralelas también hablaremos de líneas perpendiculares. Las líneas perpendiculares son dos distintivas líneas coplanarias que interceptan a un Angulo de 90°. Nota, las líneas perpendiculares tienen una pendiente reciproca que es negativa. Algunos Profesores lo llamaran pendientes reciprocas opuestas. Después hablaremos de esta. Visualmente en una grafica lo que quiere decir es que tenemos dos líneas y siempre se origina en un Angulo de 90°. Una de la pendiente es positiva y la otra es negativa cada vez. Sera algo como Primeramente, ¿Qué es una Pendiente reciproca negativa? Es el resultado de invertir la fracción y cambiar el signo. Entonces, el reciproco negativo y el reciproco opuesto quiere decir lo mismo. Esto es solo para estar seguros de tener la terminología correcta antes de empezar nuestro problema. Está Bien! Ahora varemos está pendiente es – . ¿Cómo encontraremos el reciproco negativo? M= - m =? Recuerda, negativo quiere decir cambiar el signo. Entonces, si comenzamos con negativo, ahora la pendiente de la línea perpendicular será positiva. Y la pendiente es entonces, lo invertimos y tenemos , entonces cambias el signo, inviertes la fracción y será m = y esta es la pendiente de la línea perpendicular. Ahora que sabemos esto, vamos a trabajar este: Busca la ecuación de la línea que contiene el punto (-2,-1) y es perpendicular a la línea y= x +2 Para graficar o buscar la ecuación de cualquiera línea, necesitas tener un punto y pendiente. El punto aquí es (-2,-1). ¿Cómo encontraremos la pendiente? Mira la línea que nos han dado esta en la forma de y= mx +b. Entonces, la pendiente es el número que es el coeficiente enfrente de la X. En este caso es m= , esta es la pendiente de la línea perpendicular. ¿Cómo encontraremos la pendiente de nuestra línea? Nuestra pendiente es el reciproco opuesto, entonces, línea perpendicular y el será negativo por la sera invertido, entonces, seria que es -3. Entonces la pendiente es m= -3. Ahora, tenemos pendiente, punto, y buscamos la ecuación. De nuevo tenemos: y-y1 = m(x-x1) Recuerda, x1 , y1 es nuestro orden de pares, la x es primero, la y es segundo, m es nuestra pendiente. Entonces sustituiremos, tenemos: y-(-1) = -3 (x-(-2)) tenemos que simplificar, recuerda, en matemáticas cada vez que tengas dos negativo es lo mismo que escribir positivo. Es lo primero que haremos, tendremos: y+1 = -3(x+2) Vamos a tratar de escribir este en la forma y= mx +b, pero un momento tenemos que trabajar los paréntesis. ¿Cómo lo cancelamos? Necesitamos distribuir el -3, si hacemos esto tenemos: y+1 = -3x -6 Tenemos un paso más para resolver por Y. ¿Cómo cancelamos el +1? ¿Cómo lo llevamos al otro lado? Recuerda, lo opuesto de sumar uno, seria, restar uno, en los dos lados. Entonces, y+1-1 = -3x -6 -1 El menos uno y más uno a la izquierda se cancelan y tenemos Y= y combinamos las constantes a la derecha, y tendremos, Y= -3x -7 Esta es la línea perpendicular. ¿Cómo mostraremos esta gráficamente? Vamos a graficar, entonces, Y= x +2 ¿Cómo graficaremos esta? Lo mismo que hicimos al principio. Mira la Y intercepta primero es 2, y quiere decir, desde el origen voy dos unidades hacia arriba en el eje de Y. Ahora, para buscar el segundo punto, vamos a seguir la pendiente que es hacia arriba sobre uno de los lados, o sea, cambio en Y, sobre cambio en X. En este caso es , que quiere decir voy hacia arriba uno y a la derecha tres unidades desde mi línea que intercepta. Tenemos nuestro segundo punto, ahora trazaremos nuestra línea que va en estos dos puntos. Ahora vamos a graficar la línea que decimos que es perpendicular que encontramos hace un memento. En esta la hacemos en rojo, para ver la diferencia entre las líneas. La Y que intercepta es -7 que quiere decir desde el origen en el eje X, vamos hacia abajo 7 unidades para nuestro primer punto, y la pendiente es -3 , y esta sobre entendido que es no vamos a aumentar o hacia arriba, recuerda esta es negativa, quiere decir que vamos hacia abajo 3 unidades a la derecha y si hacemos esto tenemos nuestro segundo punto. Ahora traza tu línea y notaras que si hicimos esta correctamente las dos líneas interceptan en el Angulo derecho porque son perpendiculares. Ahora las líneas paralelas son las líneas con las mismas pendientes. Líneas perpendiculares son las líneas con negativas u opuestas pendientes reciprocas. Cada grupo de líneas que no tienen la misma pendiente o pendientes reciprocas opuestas no se llamarían Ninguna de estas. Esperamos que hayas aprendido con respecto a Líneas Paralelas, Líneas Perpendiculares y las que llamaríamos Ninguna de estas.


![Prueba Segundos2[1]](http://s2.studylib.es/store/data/003397536_1-3ac4e8618b6474fb10e9bb3037bc9dd2-300x300.png)