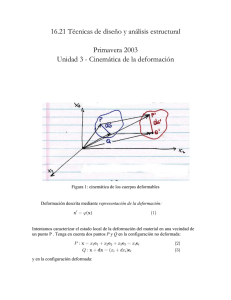
el tensor de deformación
Anuncio

Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN CAPÍTULO CAPÍTULO3: 3: EL ELTENSOR TENSORDE DEDEFORMACIÓN DEFORMACIÓN 1. Concepto de desplazamiento y deformación. 2. Deformación en el entorno de un punto. 3. Significado físico del tensor deformación y de la matriz de giro. 4. El vector deformación. Componentes intrínsecas. 5. Correlación entre el tensor de tensiones y el tensor de deformaciones. 6. Tensor esférico y tensor desviador. 7. Ecuaciones de compatibilidad. 8. Obtención del vector desplazamiento a partir del tensor de deformación 9. Tensión plana Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN CAPÍTULO CAPÍTULO3: 3: EL ELTENSOR TENSORDE DEDEFORMACIÓN DEFORMACIÓN 1. Concepto de desplazamiento y deformación. 2. Deformación en el entorno de un punto. 3. Significado físico del tensor deformación y de la matriz de giro. 4. El vector deformación. Componentes intrínsecas. 5. Correlación entre el tensor de tensiones y el tensor de deformaciones. 6. Tensor esférico y tensor desviador. 7. Ecuaciones de compatibilidad. Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN Desplazamientos en el entorno de un punto: Deformación Ya es sabido que los puntos de un sólido sometidos a unas solicitaciones sufren una variación de posición en el espacio. Q’ 2D El vector que una las posiciones inicial y final de un punto es el vector desplazamiento. Sus componentes son los desplazamientos o recorridos. r δ p = u , v, w Q(x+dx,y+dy,z+dz) δ + dδ dδ δ dr ' La deformación puede ser de dos tipos: LINEAL que representa el alargamiento lineal unitario y dr ANGULAR que representa la variación angular. dx dy = dr dz La deformación lineal es propiedad del punto y de la dirección respecto de la que se está calculando el alargamiento. La deformación angular es propiedad del punto y de las dos direcciones que forman el ángulo considerado. δ P’ P(x,y,z) Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN Desplazamientos en el entorno de un punto: Deformación P(x,y,z) P’(x+u,y+v,z+w) w v 3D Q(x+dx,y+dy,z+dz) δ + dδ u dx dr = dy dz dr Q’ w+dw v+dv dr' u+du P’ δ w P(x,y,z) v Si dos puntos P y Q de un sólido elástico están infinitamente próximos los desplazamientos de ambos serán similares. u Luego pueden desarrollarse en serie de Taylor las componentes del vector desplazamiento del punto Q en torno a P. (esto es similar a lo que se hizo con el tensor de tensiones) Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN Desplazamientos en el entorno de un punto: Deformación 3D Q P(x,y,z) P’(x+u,y+v,z+w) w Q’ Los vectores der P y rQ son:r r r desplazamiento r δ p = u p i + v p j + w p k ; δ Q = uQ i + vQ j + wQ k Por tanto, el desplazamiento de Q será: v u Que puede representarse matricialmente así: donde esta matriz puede notarse como M: que, por ser una matriz cuadrada, puede descomponerse en una matriz simétrica y otra antisimétrica: El primer sumando es el tensor de deformaciones y el segundo la matriz de giro Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN TENSOR DE DEFORMACION Análogamente se define la matriz de giro, cuya diagonal es cero y Significado físico del TENSOR DE DEFORMACION y de la MATRIZ DE GIRO dx dy x secuencia de deformación de un cuadrilátero elemental Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN significado físico y La secuencia anterior puede analizarse descomponiéndola en tres fases: 1.- Desplazamiento según OX de todo el sólido (+deformación) dx 2.- Desplazamiento según OY de todo el sólido (+deformación) dy 3.- Giro y x A C DESPLAZAMIENTO SEGÚN OX: Si el desplazamiento de A y B es u, el de C y D puede obtenerse desarrollando en serie en torno al origen, y considerando sólo la variación según X B D x Recordando la definición de ∆l deformación lineal: ε= l u u+ ∂u dx ∂x En la dirección del eje OX la deformación que se obtiene es: δu u + dx − u ∆(dx ) δu δx = = que es el término εxx del tensor de deformaciones. dx dx δx Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN significado físico y DESPLAZAMIENTO SEGÚN OY: dx Si el desplazamiento de B y D es v, el de A y C puede obtenerse desarrollando en serie en torno al origen, y considerando sólo la variación según Y. dy x y v+ Recordando la definición de ∆l deformación lineal: ε= ∂v dy ∂y (lo mismo que en el caso anterior) A C v l B D x En la dirección del eje OY la deformación que se obtiene es: ∆(dy ) = dy v+ δv dy − v δy dy = δv δy que es el término εyy del tensor de deformaciones. Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN significado físico y y dx dy x v+ ∂v ∂u (dx + dx ) = ∂x ∂x D A C v ∂v ∂u = v + 1 + dx = ∂x ∂x ∂v = v + dx ∂x B x u desp. u+ GIRO: Aquí se puede apreciar la variación del ángulo; de modo que el ángulo inicial BAC de 90º se transforma a 90º+α-β ∂u ∂v ∂u ∂v dy + dy = u + 1 + dy = ∂y ∂y ∂y ∂y =u+ ∂u dy ∂y desp. (ahora ya no hay cambio de tamaño) Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN significado físico y y dx dy β x D B v+ ∂v dx ∂x α v Puede apreciarse que α=δv//δx; como entre A y B hay una variación de la coordenada x, si se desarrolla en serie el desplazamiento en torno al punto A, para hallar el desplazamiento de C sólo influirá la variación con el eje x. El desplazamiento, según el eje y, de C será v+δv//δx, pues v es el desplazamiento de A, por tanto: tan α = v+ δv dx − v δv δx = ≅α dx δx A C x u u+ ∂u dy ∂y el mismo razonamiento sirve pata determinar que β=δu//δy esto es así porque, como las deformaciones son pequeñas, los ángulos serán pequeños, con lo que la tangente se asimila al ángulo. Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN De modo que la variación del ángulo de deformación es α+β=δv//δx+δu//δy = γ expresión que es el doble del término εxy o εyx (recuérdese que en el tensor de deformación se ha definido la deformación tangencial εxy como la mitad del ángulo girado en la deformación del sólido), de modo que se verifica esta identidad. Por este motivo, en ocasiones el tensor de deformación se escribe así: ε x SIGNIFICADO FISICO DE LAS COMPONENTES DE LA MATRIZ DE GIRO 1 γ xy 2 1 γ 2 xz y Para determinar el giro de una sección se considerará el giro de la bisectriz del ángulo que, antes de la deformación, era de 45º con la horizontal. La bisectriz, debido al efecto del ángulo α, girará α/2, y debido a β, girará β/2, con lo que el giro total de la sección será de ½(δu/δy-δv/δx), expresión que coincide con el término hyx de la matriz de giro. Por tanto las componentes de la MATRIZ DE GIRO representan el giro del prisma elemental en cada plano coordenado. Este hecho justifica su denominación. hxx [H ] = hyx hzx hxy hyy hzy hxz hyz hzz β ω δ 1 γ xy 2 εy 1 γ yz 2 1 γ xz 2 1 γ yz 2 ε z α+δ−ω= π 4 β+δ+ω= π 4 π/4 δ π/4 α x Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN CAPÍTULO CAPÍTULO3: 3: EL ELTENSOR TENSORDE DEDEFORMACIÓN DEFORMACIÓN 1. Concepto de desplazamiento y deformación. 2. Deformación en el entorno de un punto. 3. Significado físico del tensor deformación y de la matriz de giro. 4. El vector deformación. Componentes intrínsecas. 5. Correlación entre el tensor de tensiones y el tensor de deformaciones. 6. Tensor esférico y tensor desviador. 7. Ecuaciones de compatibilidad. Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN Del mismo modo que se definió un vector tensión puede definirse un vector deformación, asociado a un punto y a una dirección. SIGNIFICADO FISICO. COMPONENTES INTRINSECAS Este vector deformación puede obtenerse a partir del tensor de deformación, asociado a un punto, y de la normal al plano a partir de esta expresión: Recordando la relación entre el desplazamiento relativo de dos puntos infinitamente cercanos con el tensor de deformación y la matriz de giro, ε = [ε ]⋅ n r r r Q’ ξ 1 γ dr 2 el segundo término término, que consituye la matriz de giro, representa el giro como sólido rígido de un punto respecto a otro y el término que depende de la deformación será: r r r dδ = [ε ]⋅ dr dδ dδ donde dr es el vector de posición. Q dr' dr' r 1 + ε n dr dr dr Esa variación puede descomponerse en una variación de longitud (componente normal) y en una variación angular (componente angular). r r δ P’ P Dividiendo por el módulo del vector de posición se obtiene la expresión inicial del vector deformación. De modo que el vector deformación expresa la variación de una dirección en el proceso de deformación. ε n = ε ⋅ n → normal 1 2 εt = ⋅γ = (εr )2 − ε n2 → angular Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN CAPÍTULO CAPÍTULO3: 3: EL ELTENSOR TENSORDE DEDEFORMACIÓN DEFORMACIÓN 1. Concepto de desplazamiento y deformación. 2. Deformación en el entorno de un punto. 3. Significado físico del tensor deformación y de la matriz de giro. 4. El vector deformación. Componentes intrínsecas. 5. Correlación entre el tensor de tensiones y el tensor de deformaciones. 6. Tensor esférico y tensor desviador. 7. Ecuaciones de compatibilidad. Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 •Tensor simétrico •Componentes intrínsecas •Tensor simétrico •Componentes intrínsecas σn , τ εn , 21 γ •Tensiones y direcciones principales σI, σII, σIII ηI, ηII, ηIII 2 2 x y z + + =1 σI2 σII2 σIII2 N Ó I S TEN •Circulos de Möhr •Invariantes I 2 = σI σII + σI σIII + σII σIII = = σ x σ y + σ x σz + σ y σz − τ2xy − τ2xz − τ2yz I3 = det(σ) % •Tensiones octaédricas σ = I1 3 τoct = I − 32 I2 2 2 9 1 •Tensor esférico y desviador σ =σ I σ% D = σ −% σoct I % % % O oct •Tensión plana •Elipsoide de Lamé x 2 y2 z2 + + =1 εI2 εII2 εIII2 •Circulos de Möhr •Invariantes I1 = σ x + σ y + σz = σI + σII + σIII oct •Deformaciones y direcciones principales εI, εII, εIII η,I , η,II, η,III •Elipsoide de Lamé 2 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN DEF N Ó I C A M OR J1 = ε x + ε y + ε z = εI + εII + εIII J2 = εIεII + εIεIII + εIIεIII = = ε x ε y + ε x ε z + ε y ε z − ε2xy − ε 2xz − ε2yz J3 = det(ε) % •Deformaciones octaédricas εoct = J1 3 1 2 τoct = 2 9 J12 − 32 J2 •Tensor esférico y desviador εO = ε oct I ε% D = ε −% εoct I % % % •Deformación plana Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN CAPÍTULO CAPÍTULO3: 3: EL ELTENSOR TENSORDE DEDEFORMACIÓN DEFORMACIÓN 1. Concepto de desplazamiento y deformación. 2. Deformación en el entorno de un punto. 3. Significado físico del tensor deformación y de la matriz de giro. 4. El vector deformación. Componentes intrínsecas. 5. Correlación entre el tensor de tensiones y el tensor de deformaciones. 6. Tensor esférico y tensor desviador. 7. Ecuaciones de compatibilidad. 8. Obtención del vector desplazamiento a partir del tensor de deformación 9. Tensión plana Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN CAPÍTULO CAPÍTULO3: 3: EL ELTENSOR TENSORDE DEDEFORMACIÓN DEFORMACIÓN 1. Concepto de desplazamiento y deformación. 2. Deformación en el entorno de un punto. 3. Significado físico del tensor deformación y de la matriz de giro. 4. El vector deformación. Componentes intrínsecas. 5. Correlación entre el tensor de tensiones y el tensor de deformaciones. 6. Tensor esférico y tensor desviador. 7. Ecuaciones de compatibilidad. Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 Un invariante de un tensor es un valor del mismo que permanece inalterable si cambia el sistema de referencia. z CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN El alargamiento que sufren las tres direcciones en el espacio será: Supóngase que el prisma de la figura se ha deformado alargándose o acortándose en cada dirección del espacio. ∆(dx) = ε x ⋅ dx ; ∆(dy) = ε y ⋅ dy ; ∆(dz) = ε z ⋅ dz Consecuentemente, el incremento de volumen del sólido será: ∆V = V final − Vinicial = (...) = Incremento unitario de volumen = (ε x + ε y + ε z + ε x ⋅ ε y + ε x ⋅ ε z + + ε y ⋅ ε z + ε x ⋅ ε y ⋅ ε x )dx ⋅ dy ⋅ dz Pero los dobles y triples productos de infinitésimos son despreciables, por lo que la expresión queda reducida a: dz (1 + εz ) ∆V = (ε x + ε y + ε z )dx ⋅ dy ⋅ dz dz dy y dx dx (1 + ε x ) x dy (1 + ε y ) En el caso de que el incremento de volumen fuese unitario el producto dxdydz=1, por lo que su valor sería igual al primer invariante del tensor de deformaciones. Por otra parte se ha enunciado que el tensor esférico dependía únicamente del primer invariante; y se acaba de ver que el primer invariante del tensor de deformaciones representa un cambio unitario de volumen, luego se demuestra que el tensor esférico se relaciona, únicamente, con un cambio de volumen del sólido. Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN CAPÍTULO CAPÍTULO3: 3: EL ELTENSOR TENSORDE DEDEFORMACIÓN DEFORMACIÓN 1. Concepto de desplazamiento y deformación. 2. Deformación en el entorno de un punto. 3. Significado físico del tensor deformación y de la matriz de giro. 4. El vector deformación. Componentes intrínsecas. 5. Correlación entre el tensor de tensiones y el tensor de deformaciones. 6. Tensor esférico y tensor desviador. 7. Ecuaciones de compatibilidad. Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 Hasta ahora se ha demostrado la existencia de un tensor de deformaciones que, a partir del campo de desplazamientos, permite conocer un campo de deformaciones mediante la aplicación de las expresiones del mismo (a la derecha del todo) εx 1 γ xy 2 1 γ 2 xz CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN 1 γ xy 2 εy 1 γ yz 2 Por tanto, el conocimiento de un campo de desplazamientos que en cada punto tome un sólo valor y continuo conduce a la determinación de un campo de deformaciones, mediante la aplicación de las expresiones anteriores; pero,… ¿cualquier tensor de deformaciones lleva asociado un campo de desplazamientos, o es necesario que se verifiquen algunas condiciones adicionales? Matemáticamente, todo campo de deformaciones debe mantener la continuidad del sólido. Y para que un sólido deformado sea continuo, ha de verificar una serie de condiciones derivadas de las expresiones escritas arriba a la derecha. De modo que, haciendo las derivadas parciales segundas de las deformaciones: 1 γ xz δu δv δw 2 εx = εy = εz = δz δx δy 1 γ yz 2 γ xy = δu + δv γ yz = δv + δw γ xz = δu + δw δy δx δz δy δz δx ε z Puede enfocarse esta cuestión suponiendo que cada punto del sólido es un paralelepípedo elemental al que se asocia un tensor de deformaciones. Si el sólido se deforma se deformarán cada uno de esos infinitos paralelepípedos; las deformaciones serán compatibles si, después de haberse efectuado, esos infinitos paralelepípedos se pueden montar como un inmenso rompecabezas, y no lo serán si tras la deformación no pueden montarse. Se observa que: Que es la ECUACION DE COMPATIBILIDAD en el plano XY Considerando los tres ejes se obtienen otras dos ecuaciones Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 El proceso de determinación del resto de ecuaciones continúa del siguiente modo: CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN De estas tres expresiones se suma la primera con la segunda, se le resta la tercera y se divide el resultado entre dos. El segundo término de la expresión obtenida se obtiene derivando εx respecto de y y de z, con lo que se obtiene la CUARTA ECUACION DE COMPATIBILIDAD: Y de modo similar se obtienen la QUINTA Y LA XEXTA: RESUMIENDO: Por tanto se ha demostrado, no sin cierta pericia matemática, que si las deformaciones llevan asociados unos desplazamientos univaluados (que en cada punto toman un solo valor) y continuos, existen unas condiciones adicionales (estas seis ecuaciones de compatibilidad) que han de verificarse necesariamente. Del mismo modo puede demostrarse que si las deformaciones cumplen las ecuaciones de compatibilidad, éstas son suficientes para obtener un campo de desplazamientos univaluado y continuo. Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN CAPÍTULO CAPÍTULO3: 3: EL ELTENSOR TENSORDE DEDEFORMACIÓN DEFORMACIÓN 1. Concepto de desplazamiento y deformación. 2. Deformación en el entorno de un punto. 3. Significado físico del tensor deformación y de la matriz de giro. 4. El vector deformación. Componentes intrínsecas. 5. Correlación entre el tensor de tensiones y el tensor de deformaciones. 6. Tensor esférico y tensor desviador. 7. Ecuaciones de compatibilidad. 8. Obtención del vector desplazamiento a partir del tensor de deformación Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 El procedimiento deductivo es similar a los anteriores; deducir lo que ocurre en un punto infinitamente próximo a otro considerado, desarrollando en serie las expresiones de partida. CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN En concreto, para este caso, se supondrá que se conoce el tensor de deformaciones compatible y se desean conocer las componentes del desplazamiento de un punto; se sabe que las componentes del desplazamiento de un punto infinitamente cercano, separado de éste un vector (dx,dy,dz), al punto (x0,y0,z0) son (se escribe sólo la primera): u ( x, y, z ) = u ( x0 , y0 , z0 ) + ε x dx + (ε xy + hxy )dy + (ε xz + hxz )dz Para conocer las componentes del vector desplazamiento de un punto cualquiera, de coordenadas (x1,y1,z1), hay que integrar la expresión anterior: δu δu δu u (x1 , y1 , z1 ) = u (x0 , y0 , z0 ) + ∫ dx + ∫ dy + ∫ dz = δx δy δz P P P P1 P1 P1 0 0 0 P1 P1 P1 P0 P0 P0 = u (x0 , y0 , z0 ) + ∫ ε x dx + ∫ (ε xy + hxy )dy + ∫ (ε xz + hxz )dz El desarrollo de la expresión exige la integración por partes de las componentes de la matriz de giro; se desprecian los infinitésimos de segundo orden, se agrupan términos, se simplifica y, finalmente, resulta la componente des desplazamiento según la coordenada x a partir del tensor de deformaciones: Análogo procedimiento permite obtener el resultado para las otras dos componentes en el espacio (v y w) P1 P1 P1 P0 P0 P0 u = u0 + ∫ ε x dx + ∫ ε xy dy + ∫ ε xz dz + hxy ]P0 ⋅ (z0 + z1 ) + 1 δε δε x δε xy δε ⋅ ( y − y1 )dx + ∫ − y + xy ⋅ ( y − y1 )dy + + ∫ − δy δx δx δy P0 P0 P1 P 1 δε xz δε xy δε δε ⋅ ( y − y1 )dz + ∫ x − xz ⋅ (z − z1 )dx + + ∫ + δy δx δz δx P0 P0 P1 P 1 δε xy δε yz δε δε ⋅ (z − z1 )dy + ∫ xz − z + ∫ − δz δx δz δx P0 P0 P1 P ⋅ (z − z1 )dz De modo que se habrán determinado tres expresiones que permiten conocer el desplazamiento de un punto cualquiera conocidos el desplazamiento en otro punto cualquiera, la matriz de giro y el tensor de deformaciones en todo el dominio. Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN CAPÍTULO CAPÍTULO3: 3: EL ELTENSOR TENSORDE DEDEFORMACIÓN DEFORMACIÓN 1. Concepto de desplazamiento y deformación. 2. Deformación en el entorno de un punto. 3. Significado físico del tensor deformación y de la matriz de giro. 4. El vector deformación. Componentes intrínsecas. 5. Correlación entre el tensor de tensiones y el tensor de deformaciones. 6. Tensor esférico y tensor desviador. 7. Ecuaciones de compatibilidad. 8. Obtención del vector desplazamiento a partir del tensor de deformación 9. Deformación plana Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga Elasticidad y resistencia de materiales. Curso 2008/2009 CAPÍTULO 3: EL TENSOR DE DEFORMACIÓN Existen determinados problemas que se pueden representar por un tensor de deformaciones de segundo orden; son los problemas de DEFORMACION PLANA. Físicamente estos problemas responden a sólidos en los que una dimensión es mucho mayor que las otras dos y las fuerzas se encuentran aplicadas según esas dos dimensiones menores. En este tipo de situaciones la deformación según la dimensión mayor es nula: suponiendo que en esa dirección se establezca el eje OZ serían nulos los términos εx, γxz y γyz, luego el tensor de deformación se puede reducir a: r εx [ε ] = 1 γ xy 2 1 γ xy 2 ε y Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga