1) Filtros de rechazo de banda. ξ

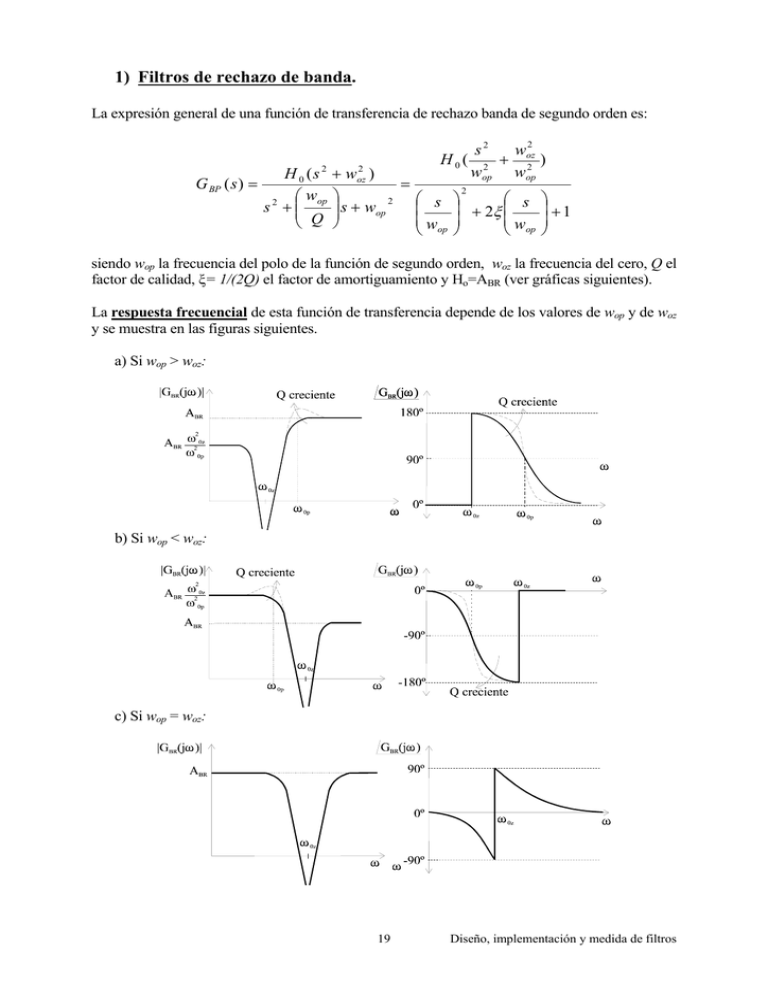
1) Filtros de rechazo de banda.
La expresión general de una función de transferencia de rechazo banda de segundo orden es:
H0(
G BP ( s ) =
woz2
s2
+
)
2
2
wop
wop
H 0 ( s 2 + woz2 )
=
2
w


op
 s + wop 2  s  + 2ξ  s
s 2 + 
w 
w
 Q 
 op 
 op

 +1


siendo wop la frecuencia del polo de la función de segundo orden, woz la frecuencia del cero, Q el
factor de calidad, ξ= 1/(2Q) el factor de amortiguamiento y Ho=ABR (ver gráficas siguientes).
La respuesta frecuencial de esta función de transferencia depende de los valores de wop y de woz
y se muestra en las figuras siguientes.
a) Si wop > woz:
b) Si wop < woz:
c) Si wop = woz:
19
Diseño, implementación y medida de filtros
Para calcular los parámetros del filtro a partir de su respuesta frecuencial, se medirá la ganancia
en alta y baja frecuencia y la frecuencia a la que la ganancia es mínima. Con esto tenemos Ho,
woz y wop. Para obtener Q, haremos dos medidas distintas dependiendo de si el filtro es simétrico
o no.
•
Si el filtro no es simétrico (woz ≠ wop), se medirá la ganancia a la frecuencia wop. Se
verifica:
G ( s) =
H o × ( woz2 − w 2 )
w − w + jw
2
op
2
wop
⇒
H o2 × ( woz2 − w 2 ) 2
G ( s) =
 wop
( w − w ) +  w
 Q
2
op
Q
2
2




2
Si w=wop, se verifica:
G ( s) = Q ×
•
2
)
H o × ( woz2 − wop
2
wop
Si el filtro es simétrico (woz = wop), se medirá el ancho de banda de -3dB y se verifica:
BW = BW H − BW L =
wop
Q
La función de transferencia de rechazo de banda se puede expresar como:
G BRF ( s ) = G LPF ( s ) + G HPF ( s ) =
H0s2
H 0 woz2
+
w 
 wop 
 s + wop 2 s 2 +  op  s + wop 2
s 2 + 
 Q 
 Q 
Por tanto, la respuesta temporal, c(t), de un filtro de rechazo de banda de segundo orden
subamortiguado (0<ξ<1) a una entrada escalón unitario, u(t), se obtiene sumando las respuestas
temporales ya conocidas del filtro paso bajo y del filtro paso alto en que se descompone.
Las ecuaciones que permiten obtener los parámetros Ho, ξ, woz y ωop a partir de la respuesta
temporal al escalón unitario de un filtro de rechazo de banda de segundo orden son distintas
dependiendo de si el filtro es simétrico o no simétrico. Se verán los dos casos por separado.
20
Diseño, implementación y medida de filtros
En la figura, se muestra gráficamente la respuesta temporal al escalón unitario de una función
de transferencia de segundo orden de tipo rechazo de banda en la que H0=2.5, ξ=0.2, woz=0.3
y wop=1.
Las ecuaciones que permiten obtener los parámetros Ho, ξ, woz y ωop a partir de la respuesta
temporal al escalón unitario de un filtro de rechazo de banda de segundo orden no simétrico
son las que se indican a continuación.
1)
El valor de Ho se obtiene midiendo la respuesta en el instante t=0:
H o = c(t = 0)
2)
Midiendo la respuesta en estado estacionario se obtiene:
H oL
3)
w
= H o  oz
w
 op
2

 = c(t → ∞)


Se puede calcular ξ de varias maneras. Una de ellas es midiendo la respuesta en
t=T/2, siendo T el periodo del transitorio de c(t), y se obtiene:
ξ=
  c(t = T / 2) − H oL
ln
H oL − H o
 
  c(t = T / 2) − H oL
π + ln
H oL − H o
 
2
4)



2



2
El parámetro ωop se obtiene con la expresión siguiente:
ω op =
2π
T 1− ξ 2
21
Diseño, implementación y medida de filtros
En la figura, se muestra gráficamente la respuesta temporal al escalón unitario de una función
de transferencia de segundo orden de tipo rechazo de banda simétrica en la que Ho = 1, ωop =
woz=1 y ξ = 0.2.
Las ecuaciones que permiten obtener los parámetros Ho, ξ, woz=ωop a partir de la respuesta
temporal al escalón unitario de un filtro de rechazo de banda de segundo orden simétrico son
las que se indican a continuación.
1) El valor de Ho se obtiene midiendo la respuesta en el instante t=0:
H o = c(t = 0)
2) Se puede calcular ξ de varias maneras. Una de ellas es midiendo la respuesta en
t=T/4 y en t=3T/4, siendo T el periodo del transitorio de c(t), y se obtiene:
ξ=
  H o − c(t = T / 4) 

ln
  c(t = 3 × T / 4) − H o 
2
  H o − c(t = T / 4) 

π + ln
  c(t = 3 × T / 4) − H o 
2
2
3) El parámetro ωop=woz se obtiene con la expresión siguiente:
ω op =
2π
T 1− ξ 2
22
Diseño, implementación y medida de filtros