Determinar si una función es par o impar

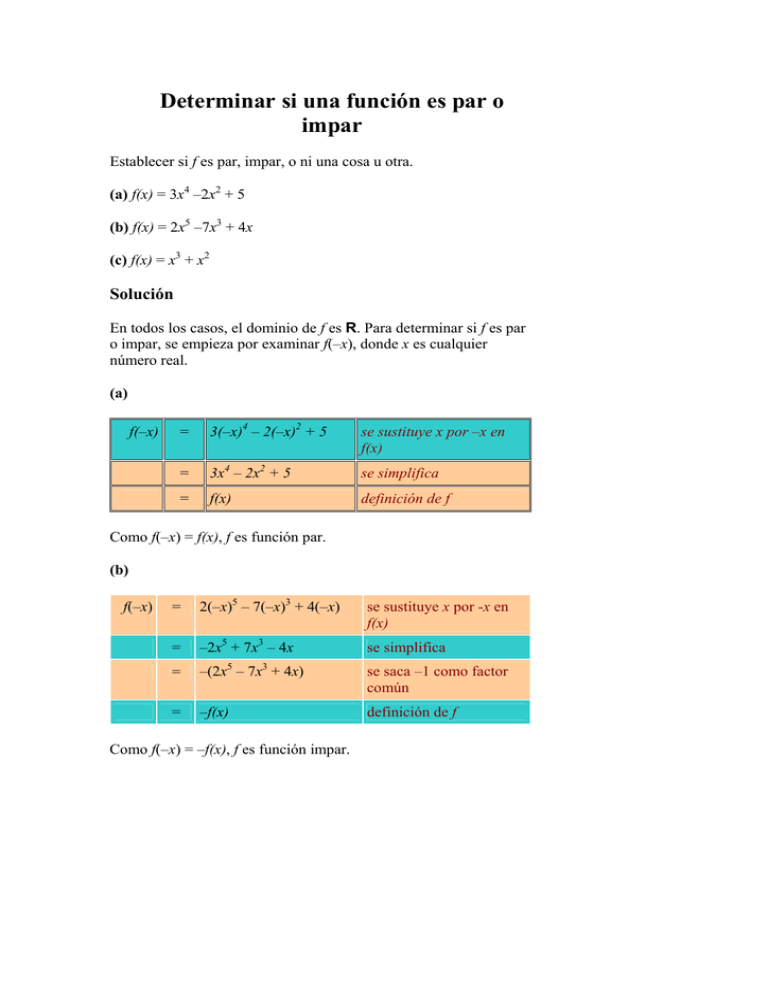
Determinar si una función es par o
impar
Establecer si f es par, impar, o ni una cosa u otra.
(a) f(x) = 3x4 –2x2 + 5
(b) f(x) = 2x5 –7x3 + 4x
(c) f(x) = x3 + x2
Solución
En todos los casos, el dominio de f es R. Para determinar si f es par
o impar, se empieza por examinar f(–x), donde x es cualquier
número real.
(a)
f(–x)
=
3(–x)4 – 2(–x)2 + 5
se sustituye x por –x en
f(x)
=
3x4 – 2x2 + 5
se simplifica
=
f(x)
definición de f
Como f(–x) = f(x), f es función par.
(b)
f(–x)
=
2(–x)5 – 7(–x)3 + 4(–x)
se sustituye x por -x en
f(x)
=
–2x5 + 7x3 – 4x
se simplifica
5
3
=
–(2x – 7x + 4x)
se saca –1 como factor
común
=
–f(x)
definición de f
Como f(–x) = –f(x), f es función impar.
(c)
f(–x)
=
(–x)3 + (–x)2
se sustituye x por -x en f(x)
=
–x3 + x2
se simplifica
Como f(–x) ≠ f(x), y f(–x) ≠ –f(x) (nótese que –f(x) = –x3 – x2), la
función f ni es par ni impar.