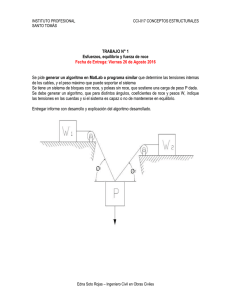
∑ ∑ ∑ ∑

Roce
Conceptos importantes acerca del Roce:
Definición: Fuerza resistente que actúa sobre un cuerpo e impide o retarda el desplazamiento de este sobre una
determinada superficie de contacto.
Actúa tangencialmente a la superficie de contacto y en sentido opuesto al movimiento.
Existen dos (2) tipos de Roce:
Roce Fluido: Las superficies de contacto están separadas por una película delgada de un fluido. También depende la
velocidad del fluido y de la resistencia de este a fuerzas de corte. Este tipo de roce se estudia en los ramos de
mecánica de fluidos
Roce seco (fricción de Coulomb): Ocurre entre superficies en contacto en ausencia de fluido lubricante. Este es el
tipo de roce que se estudiará en el presente ramo.
Teoría del Roce Seco:
La fuerza resultante de interacción de B sobre A puede descomponerse en:
1.- Una fuerza perpendicular al plano tangente de contacto llamada normal (N)
2.- Una fuerza que pertenece al plano de contacto, llamada fuerza de fricción o roce
(F)
3.- Experimentalmente se ha determinado que Fs es directamente proporcional a la
fuerza normal N. Esto puede expresarse matemáticamente como: Fs = μs · N, en
donde la constante de proporcionalidad μs es llamada coeficiente de roce estático
Ejemplos:
1.- Determine la posición de la fuerza normal. ¿Que podría pasar al aumentar la fuerza P?
Si el cuerpo está en reposo, en la superficie habrá una distribución de
fuerzas normales DNn (que equilibran el peso W) y de roce DFn (que
equilibran la fuerza P).
La línea de acción de la resultante F de la fuerza de roce pasa a través de
la superficie de contacto y la línea de acción de N pasa a una distancia
horizontal x del centro de gravedad del bloque.
Haciendo equilibrio de fuerzas se obtiene, las ecuaciones son las
siguientes:
∑F = 0 : F = P
∑F = 0 : N = W
∑ M = 0 : W · x − P ·h = 0
x
y
x=
P ·h
W
0
Si hacemos crecer P hasta que se rompe el equilibrio, podrían ocurrir dos cosas:
a) Deslizamiento horizontal en la dirección de P
∑F
y
= 0 : P = F = µs ·N, pero N = W
Por lo tanto, P = µs ·W , para que exista deslizamiento, P debe ser mayor que µs ·W .
CA/ar/jpa
Este texto fue realizado en base a los apuntes de Estática de estructuras del profesor Rodrigo Delgadillo
b) Volcamiento del bloque (rotación respecto de la esquina inferior derecha)
Si el coeficiente de roce fuera tan grande que no permitiera el deslizamiento, el bloque volcaría para un
determinado valor de P. Para este caso, la fuerza normal se desplazaría hacia la derecha hasta que quede en el
punto A, esto correspondería a que toda la masa del bloque descanse sobre
este punto. Haciendo sumatoria de momento con respecto a la esquina inferior
derecha (A), se obtiene:
∑M
A
= 0 : P ·h − W · a
2
De aquí obtenemos que el valor de la fuerza en el equilibrio es:
P=
W· a
2· h
Entonces para que ocurra volcamiento, la fuerza P deberá ser mayor que
W· a
2· h
2.- Al cilindro de peso W y radio r se la aplica un momento M. Si los coeficientes de fricción
estático μs son los mismos en los dos puntos de apoyo, determine la magnitud máxima de M
que puede ser aplicada al cilindro para que no rote.
Primero es importante realizar el diagrama de cuerpo libre. Una vez identificadas las fuerzas
que actúan sobre el cilindro, se escriben las ecuaciones de la estática.
∑M
o
= 0: FrA · r + FrB · r = M
µs · NA + µs · NB =
∑F
x
M
r
= 0: NA = FrB
NA = µs · NB
∑F
y
= 0: NB + FrA = W
µs · NA + NB = W
(1)
(2)
(3)
Reemplazando (2) en (3), obtenemos:
NB ( µs 2 + 1) = W
Y despejando resultan:
NB =
µ·W
W
y NA = s2
2
( µs + 1)
( µs + 1)
Finalmente, reemplazando NB y NA en (1), obtenemos la siguiente expresión:
µs ·
µs · W
W
M
+ µs ·
=
2
2
( µs + 1)
( µs + 1) r
µ 2 + µ 
M =  s 2 s  W ·r
 µs + 1 
CA/ar/jpa
Este texto fue realizado en base a los apuntes de Estática de estructuras del profesor Rodrigo Delgadillo
3.- Realice el siguiente ejercicio y entréguelo resuelto al comienzo
del primer certamen.
La base mostrada en la figura tiene una masa de 75 kg y se ajusta
con soportes en A y en B. El coeficiente de fricción estático entre
los soportes y el piso es de 0.3. Si una fuerza P de 500 N de
magnitud se aplica en la esquina C. Determine el rango de valores
de θ para los cuales la base no se moverá. (Recuerde considerar
volcamiento y deslizamiento).
CA/ar/jpa
Este texto fue realizado en base a los apuntes de Estática de estructuras del profesor Rodrigo Delgadillo