147 CAPÍTULO X: REACCIONES QUE INVOLUCRAN GASES 10.1
Anuncio

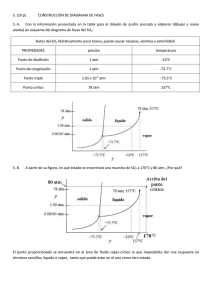
Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X CAPÍTULO X: REACCIONES QUE INVOLUCRAN GASES 10.1. INTRODUCCIÓN En el capítulo VIII se vio que la ausencia de fuerzas interatómicas entre los átomos de los gases ideales provoca que el calor de mezcla de estos gases sea cero. Esta situación representa un extremo en el rango de las posibles situaciones. En el otro extremo de este rango está la situación en la cual los gases a mezclar presentan una elevada afinidad química. Por ejemplo, una considerable cantidad de calor es liberada cuando hidrógeno y oxígeno gaseosos se mezclan en presencia de un catalizador. La termodinámica de este sistema puede ser tratado de dos maneras. 1- La mezcla puede considerarse no ideal y su estado de equilibrio a T y P (total) puede describirse en término de la fugacidad de los componentes. 2- Los dos componentes reaccionan y dan lugar a la aparición de un producto. Si la presión del sistema es suficientemente baja, el estado de equilibrio a T puede ser descrito en términos de las presiones parciales. Aunque ambos tratamientos son termodinámicamente equivalentes, el 2º por su correspondencia con la realidad física es más conveniente y práctico. Como en cualquier sistema a temperatura y presión constantes, el estado de equilibrio es aquel en el cuan la energía libre de Gibbs del sistema es la mínima. Si los gases, presentes inicialmente en el sistema, reaccionan para formar distintas especies, el cambio total en la energía libre del sistema comprende las contribuciones provenientes de la reacción química y de la mezcla de los productos con los reactivos remanentes. El conocimiento de la variación de este cambio de energía libre con la composición (la que varía desde los gases reactivos puros sin mezclar hasta los productos puros sin mezclar) permite la determinación del estado de equilibrio en cualquier sistema de gases reactivos. Esta determinación se ve facilitada por la introducción de la constante de equilibrio de la reacción y puede ser verse que la relación entre al constante de equilibrio y el cambio en la energía libre estándar de la reacción es una de las relaciones más importante en el equilibrio termodinámico de una reacción. Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 147 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X 10.2. EQUILIBRIO EN UNA REACCIÓN DE MEZCLA DE GASES Y LA CONSTANTE DE EQUILIBRIO. Consideremos la reacción A(g) + B(g) = 2C(g) que ocurre a temperatura T y presión P constantes. En cualquier instante de la reacción la energía libre de Gibbs del sistema es G’ = nA G A + nB GB + nC GC (10.1) donde nA, nB y nC son los números de moles de A, B y C presentes en el sistema de reacción en ese instante y G A , GB y GC son las energías libres parciales molares de A, B y C en la mezcla de gases que ocurre a ese instante. El problema es determinar los valores de nA, nB y nC que minimizan el valor de G’ en la ecuación 10.1 y ese será el estado de equilibrio de ese sistema a P y T dadas. Esto es, la reacción química entre A y B procederá hasta que la energía libre del sistema sea minimizada y ahí se detendrá. La estequiometría de la reacción permite que el número de moles de todas las especies presentes en un instante sean expresados en términos de una de las especies. Comenzando con un mol de A y un mol de B, como 1 átomo de A reacciona con 1 átomo de B para producir 2 moléculas de C, luego, en cualquier instante de la reacción: nA = nB, y nC = 2 - nA - nB = 2 (1 – nA) La ecuación 10.1 puede ahora ser escrita como G’ = nA G A + nA GB + 2 (1 – nA) GC la XC = 2 (1 − n A ) = (1 − n A ) , substituyendo da 2 ( ecuación 7.15 Gi = G iº + RT ln x i + RT ln P De y n XA = A , 2 n XB = B , 2 ) n º º + 2 GC + 2 R T ln P + 2 R T n A ln A + (1 − n A )ln (1 − n A ) o G′ = n A G ºA + GBº − 2 G C 2 n º G′ − 2 G C = n A (− ∆Gº ) + 2 R T ln P + 2 R T n A ln A + (1 − n A )ln (1 − n A ) 2 (10.2) º − G ºA − GBº es el cambio en energía libre estándar para la reacción química a donde ∆Gº = 2 G C la temperatura T. El cambio en la energía estándar para cualquier reacción es la diferencia entre la suma de las energías libres de los productos y la suma de las energías libres de los reactivos, ambos en sus estados estándar. En el presente caso ∆Gº es la diferencia entre la energía libre de 2 moles de C a 1 atm de presión y una temperatura T y 1 mol de A y 1 mol de Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 148 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X B, cada uno a 1 atm de presión y la temperatura T. Si la presión total del sistema es 1 atm, la ecuación 10.2 se simplifica n º G′ − 2 G C = n A (− ∆Gº ) + 2 R T n A ln A + (1 − n A )ln (1 − n A ) 2 (10.3) El lado izquierdo de la ecuación 10.3, que es la diferencia entre la energía libre de Gibbs de un sistema de 2 moles cuando nA = nA y la energía libre de Gibbs del sistema cuando este consiste en 2 moles de C, está determinado por dos factores: 1. El cambio en energía libre debido a la reacción química, o sea la desaparición de reactivos producto de la aparición de productos de reacción, dado por el primer término en el lado derecho de la ecuación 10.3. 2. La disminución de energía libre causada por la mezcla de los gases, dado por el segundo término en le lado derecho de la ecuación 10.3. La figura 10.1 es el gráfico para la reacción A(g) + B(g) = 2C(g) a 500K y 1atm de presión. Figura 10.1 º º ∆G 500 para la reacción es -5 kJ. Si arbitrariamente se elige (G ºA + GBº ) = 0, luego 2 G C = -5kJ. En la figura 10.1 la ordenada ∆G’ está dibujada como la diferencia entre la energía libre del Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 149 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X sistema conteniendo nA moles de A y la energía libre del sistema con un mol de A y un mol de B antes de que ocurra la mezcla de A y B. Luego el punto L (nA=1 y nB=1, antes de la mezcla) está ubicado a ∆G’=0, y el punto Q (nC=2) está ubicado a ∆G’=-5kJ. El punto M representa la disminución en energía libre de Gibbs debida a la mezcla de 1 mol de A y 1 mol de B antes de que la reacción química entre los dos ocurra, de la ecuación 7.20 ∆G (L → M) = p p p ∑ niRT ln Pii = R T n A ln PAA + nB ln PBB i Pero nA = nB = 1 y PA = PB = Pmezcla = 1 en cuyo caso pA = pB = ½ . Luego ∆G (L → M) = 8.3144 (J/mol K) x 500 K x 2 x ln 0.5 = -5763 J = -5,763 kJ o G’+5 kJ=1x5 kJ-5,763 kJ y por lo tanto G’=-5,763 kJ y también ∆G’=G’- (G ºA + GBº ) =-5,763 kJ. La curva I que representa la variación de G’ con nA se obtiene como la suma de la línea II (dada por el 1º término del lado derecho de la ecuación10.3 – la disminución en energía libre de Gibbs debida a la reacción química) y la curva III (dada por el 2º término de la ecuación 10.3 – la disminución en energía libre debido a la mezcla de los gases). Como se puede apreciar, la magnitud de la contribución de la reacción química a la disminución de la energía libre del sistema aumenta linealmente con el aumento de nC, pero la magnitud de la contribución al cambio en la energía libre de Gibbs debido a la mezcla de los gases pasa por un máximo en la composición R, que es la composición que permite que la mezcla de gases tenga una mayor configuración al azar. Futuras reacciones químicas, que saquen a la composición del sistema del punto R, decrecen la magnitud de la contribución de la mezcla de gases ya que incrementos en nC, a expensas de nA y nB, disminuyen el ordenamiento al azar del sistema. Eventualmente se alcanza la composición S y en ese estado la suma de las dos contribuciones a la disminución de la energía libre es máxima. Si la reacción continúa después de S, como la disminución de la línea II es menor que le incremento en la curva III, la energía libre total del sistema incrementaría. La composición S es por lo tanto aquella para la cual la energía libre del sistema tiene su valor mínimo y por lo tanto es el estado de equilibrio. La posición del mínimo en la curva I está fijado por el criterio que en el mínimo ∂G′ ∂n A =0 T, P ∂G′ = GA + GB − 2 GC = 0 (recordar + y como G’ = nA G A + nA GB + 2 (1 – nA) GC luego ∂n A T, P que n A d GA + nB d GB + n C d GC = 0 por la ecuación de Gibbs-Duhem) Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 150 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez el criterio de equilibrio para la reacción es GA + GB = 2 GC CAPÍTULO X (10.4) La ecuación 10.4 puede escribirse como º + 2 R T ln p C G ºA + R T ln p A + GBº + R T ln p B = 2 G C (10.5) donde pA, pB y pC son las presiones parciales de A, B y C en el equilibrio. Reordenando la ecuación 10.5 da º 2 GC − G ºA − GBº = − R T ln p2 o ∆Gº = − R T ln C p A pB p A pB 2 pC (10.6) El cociente de las presiones parciales de los reactantes y productos se denomina constante de equilibrio de la reacción Kp. p2 C p p A B =K p eq (10.7) y por lo tanto ∆Gº = − R T ln K p (10.8) Como ∆Gº es función sólo de la temperatura, Kp también será sólo función de la temperatura. Para el ejemplo usado en la figura 10.1 ln K p = − ∆Gº 5 000 J = = 1,203 por lo tanto Kp= 3,329. R T 8.3144 J / mol K × 500 K Ahora K p = 2 pC p A pB = 2 2 XC P X A P XB P = 2 XC X A XB = (1 − n A )2 n 2A / 4 = 3,329 y por lo tanto nA=0,523 (la otra solución nA=11.4 no es posible). Esto indica que el equilibrio de la reacción se logra con nA=nB=0,523 y nC=0,954 o cunado la reacción química A + B = 2C ha avanzado un 47.7%. El mínimo en la curva I en la figura 10.1 ocurre a nA=0,523. Si la temperatura T es tal que ∆Gº para la reacción es cero, no habrá contribución de la reacción química a ∆G’, y la variación de ∆G’ con nA estará dado por la curva III de la figura 10.1, el criterio para el equilibrio de la reacción será la maximización del ordenamiento al azar del sistema, que ocurre a la composición R. De la ecuación 10.8 si ∆Gº=0, luego Kp= 1 y por lo tanto 1= 4 (1 − n A )2 n 2A y nA = 2 3 El mínimo en la curva III ocurre a nA = nB= nC = 2/3 y por lo tanto la máxima configuración al azar en el sistema ocurre cuando las tres especies se encuentran en la misma cantidad. Es Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 151 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X importante notar que el mínimo en la curva I de la figura 10.1, que representa el estado de equilibrio del sistema a P=1 atm y 500 K, es el único punto de la curva I que tiene algún significado desde el punto de vista de la termodinámica clásica. El punto S es el único estado en la curva I que cae en la superficie de equilibrio en el espacio P-T-composición para valores fijos de P=1 atm y T=500 K. Cualquier cambio en P y/o T mueve la composición de equilibrio sobre la superficie de equilibrio P-T-composición. 10.3. EL EFECTO DE LA TEMPERATURA EN LA CONSTANTE DE EQUILIBRIO La posición del mínimo en la curva I está determinado por la diferencia entre las longitudes de LM y NQ. La longitud de LM es la disminución en la energía libre de Gibbs causada por la mezcla de gases antes de que la reacción comience, y la longitud NQ es el cambio en la energía libre estándar, ∆Gº, para la reacción. Las longitudes de esas dos líneas son dependientes de la temperatura, LM = 2 R T ln 0,5 y NQ = ∆Gº. El efecto de la temperatura en la composición a la cual el mínimo ocurre en la curva I (y por lo tanto en el valor de Kp) depende de los efectos relativos de la temperatura en las longitudes de LM y NQ. Para unos reactivos dados, la longitud de LM aumenta linealmente con la temperatura, y la variación de la longitud NQ con la temperatura está determinada por el signo y magnitud del cambio en la entropía estándar para la reacción de acuerdo con ∂∆Gº = −∆Sº ∂T P Si ∆Sº es negativo, un aumento de temperatura aumenta la longitud de LM y disminuye la de NQ. Por lo tanto la posición del mínimo en la curva se desplaza hacia la izquierda, lo cual indica que Kp disminuye con el aumento de temperatura. La variación exacta de Kp con la temperatura se obtiene considerando la ecuación de GibbsHelmholzt (4.37a) ∆Hº ∂ (∆Gº / T ) como ∆Gº= -R T ln Kp luego =− ∂T P T2 ∂ ln K p ∂T = ∆Hº RT 2 (10.9) o ∂ ln K p 1 ∂ T =− ∆Hº R (10.10) La ecuación (10.10) se conoce como la ecuación de van’t Hoff, muestra que el efecto de la temperatura sobre Kp está determinado por el signo y magnitud de ∆Hº para la reacción. Si ∆Hº es positivo, o sea reacción endotérmica, Kp aumenta con el aumento de temperatura, Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 152 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X inversamente si ∆Hº es negativo, o sea reacción exotérmica, Kp disminuye con el aumento de temperatura. La integración de la ecuación (10.10) requiere el conocimiento de la dependencia de ∆Hº con la temperatura, la cual depende del valor de ∆cp para la reacción. La dirección de la variación de Kp con la temperatura puede obtenerse del de la aplicación del principio de Le Chatelier. Si se añade calor a un sistema en equilibrio de reacción, el equilibrio se desplazará en la dirección que involucre absorción de calor. Consideremos la simple reacción gaseosa Cl2 = 2 Cl. Esta reacción es endotérmica y por lo tanto tiene un valor positivo 2 de ∆Hº, por lo tanto la constante de equilibrio Kp= p Cl p Cl2 , aumenta con el aumento de temperatura y el equilibrio se desplaza en la dirección que involucre absorción de calor. Si la 2 reacción se escribe como 2 Cl = Cl2, como la reacción tiene un ∆Hº negativo, K p = p Cl2 p Cl disminuye con el aumento de temperatura y el equilibrio se desplaza en la dirección que involucre absorción de calor. En ambos casos un aumento de temperatura incrementa pCl y disminuye p Cl2 . La ecuación (10.10) muestra que si ∆Hº es independiente de la temperatura, luego Kp varía linealmente con 1/T. 10.4. EL EFECTO DE LA PRESIÓN EN LA CONSTANTE DE EQUILIBRIO La constante de equilibrio, Kp, definida por la ecuación (10.7) es independiente de la presión. Esto es una consecuencia del hecho que ∆Gº, siendo la diferencia entre las energías libres de los productos puros ( cada uno a presión unitaria) y las energías libres de los reactantes puros (cada uno a presión unitaria), es por definición independiente de la presión. Sin embargo, el equilibrio de reacción expresado en términos del número de moles de las especies presentes es dependiente de la presión total si la reacción involucra un cambio en el número total de moles presentes. Consideremos otra vez la reacción Cl2 = 2 Cl, la reacción completa causa que se doble el número de moles presentes y el efecto de un cambio en la presión puede obtenerse nuevamente por la aplicación del principio de Le Chatelier. Si la presión ejercida sobre un sistema en el equilibrio de reacción se aumenta, el equilibrio se desplazará en la dirección que tienda a disminuir la presión ejercida en el sistema, o sea en la dirección que signifique disminuir el número de moles presentes. Por lo tanto, si la presión ejercida en el sistema Cl-Cl2 es aumentada, el equilibrio irá hacia el lado de Cl2, ya que el número total de moles presentes debe disminuir para acomodar el incremento de presión. Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 153 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X Específicamente, el efecto de la presión en el equilibrio de reacción expresado en términos del número de moles presentes (o en términos de la fracción molar) puede verse como sigue: Kp = 2 p Cl p Cl2 la cual es independiente de la presión es = 2 X Cl P2 X Cl2 P = 2 X Cl P X Cl2 = Kx P donde KX es la constante de equilibrio expresada en términos de las fracciones molares. Por lo tanto si la presión aumenta, KX debe disminuir de manera de mantener Kp constante, y la disminución de KX se alcanza moviendo el equilibrio e la reacción hacia el lado Cl2 de modo tal que X Cl disminuye y X Cl2 aumenta. En el caso de la reacción A + b = 2C, el sistema todo el tiempo tiene dos moles de gas, y por lo tanto el equilibrio de reacción, expresado en términos de fracciones molares es independiente de la presión. Kp = 2 pC p A pB = 2 2 XC P X A P XB P = 2 XC X A XB = KX Esto también puede ser visto en la ecuación (10.2), si P≠1, luego el efecto de que el término 2 R T ln P no sea cero, es la subida o bajada de la curva I en la figura 10.1, sin que se afecte la posición del mínimo con respecto al eje de composición. La magnitud del efecto del cambio de presión en el valor de KX depende del cambio en el número de moles presentes en el sistema, que ocurre como resultado de la reacción química. Para la reacción general aA + bB = cC + dD d p cC p D d X cC X D PcP d = = K X P (c + d − a − b ) lo que muestra que KX es independiente de la Kp = a b a b a b p A pB X A X B P P presión total sólo si c + d – a – b = 0. 10.5. EQUILIBRIO DE REACCIÓN COMO UN COMPROMISO ENTRE ENTALPÍA Y ENTROPÍA. La energía libre de Gibbs de un sistema se ha definido como G = H – T S y por lo tanto bajos valores de G se obtienen con bajos valores de H y grandes valores de S. Se vio, en la discusión de sistemas de un componente, que el equilibrio ocurre como el resultado de un compromiso entre consideraciones entálpicas y entrópicas. Discusiones similares se pueden hacer con respecto al equilibrio en reacciones químicas. Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 154 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X Consideremos otra vez la reacción Cl2 = 2 Cl. Esta reacción tiene un valor positivo de ∆Hº (∆Hº es la energía térmica requerida para romper el número de Avogadro de enlaces Cl-Cl) y un valor positivo de ∆Sº (2 moles de Cl son producidos por un mol de Cl2). Por lo tanto el sistema con Cl atómico tiene un alto valor de H y un alto valor de S y el sistema con Cl2 molecular tiene un bajo valor de H y un bajo valor de S. El mínimo valor de G estará en algún lugar entre los dos estados extremos. Este compromiso entre entalpía y entropía es análogo al compromiso entre la contribución de la reacción química y la mezcla de gases que produce el descenso de energía libre mostrado en la Figura 10.1. Para la reacción A + B = 2C, la ecuación (10.3) puede escribirse como n º = n A (− ∆Hº ) + n A (T∆Sº ) + 2 R T n A ln A + (1 − n A )ln (1 − n A ) G′ − 2 G C 2 = [n A (− ∆Hº )] + T n A ∆Sº +2 R nA + (1 − n A )ln (1 − n A ) n A ln 2 (10.11) El término en el primer corchete es la contribución de la entalpía al cambio en energía libre de Gibbs, y el segundo término en el lado derecho de la ecuación es la contribución de la entropía, siendo nA ∆Sº el cambio de entropía causado por la reacción química y n 2 R n A ln A + (1 − n A )ln (1 − n A ) el cambio de entropía causado por la mezcla de los gases. 2 En el ejemplo anterior ∆Gº= -5000 J a 500 K, si ∆Hº = -2500 J y ∆Sº = 5 J/K la figura 10.2 se puede dibujar apartir de la figura 10.1 En la figura 10.2 la línea ∆H’ es el primer término del lado derecho de la ecuación 10.11 y la º curva T∆S’ es el segundo término. La suma de esos dos da G’ – 2 G C , la escala de la cual está dada en el lado izquierdo de la figura 10.2. La escala en el lado derecho de la figura es ∆G’, donde como antes la referencia cero para la energía libre de Gibbs es elegida como º (G ºA + GBº ) =0, de modo tal que ∆G’ = G’ y por eso la escala está desplazada en 2 G C = -5000 J. En esta escala la curva ∆G’ en la figura 10.2 es idéntica a la curva I de la figura 10.1. Como se puede apreciar, el mínimo en la curva ∆G’ es determinado como un compromiso entre el mínimo valor de H’ a nA=0 y el máximo valor de T∆S’ a nA= = 0.597 (punto M en la figura 10.1). Si la temperatura se incrementa, el término T∆S’ se vuelve más importante, y, por lo tanto, el valor de nA de equilibrio aumenta (el mínimo en la curva de ∆G’ se desplaza hacia la izquierda. Por lo tanto, Kp disminuye con el aumento de la temperatura de acuerdo con la ecuación 10.9 ya que ∆Hº es negativo. Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 155 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X Figura 10.2 El efecto de la temperatura en la curva ∆G’ está ilustrado en la figura 10.3, en la cual las curvas para la reacción A + B = 2 C están dibujadas para 500, 1000 y 1500 K. Figura 10.3: Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 156 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X Se asume que ∆cp para esta reacción es cero, en ese caso ∆Hº y ∆Sº son independientes de la temperatura. Como ∆Gº = ∆Hº - T ∆Sº, luego º ∆G 500 = -2500 – (500 x 5) = -5000 J Kp, 500 = 3.329 º ∆G1000 = -2500 – (1000 x 5) = -7500 J Kp, 1000= 2.465 º ∆G1500 = -2500 – (1500 x 5) = -10000 J Kp, 1500= 2.229 Los valores de equilibrio de nA a 500, 1000 y 1500 son 0.523, 0.560 y 0.572, respectivamente. A pesar que Kp es constante a temperatura constante, un infinito número de presiones parciales de los reactantes y productos corresponden al valor fijado de Kp. Si la reacción involucra tres especies, la elección arbitraria de las presiones parciales de dos de ellas fijará inevitablemente la presión parcial de equilibrio de la tercera. 10.6. EQUILIBRIO DE REACCIÓN EN EL SISTEMA SO2(g)-SO3(g)-O2(g) Consideremos el equilibrio SO2(g)+ 1 O2(g)= SO3(g) 2 El cambio en energía libre estándar para esta reacción es ∆Gº = -94600 + 89,37 T (J) º =-5230 J Por lo tanto a 1000K ∆G1000 ln K p = − 5 230 J ∆Gº = = 0,629 R T 8.3144 J / mol K × 1000 K y K p = 1,876 = p SO3 1 p SO2 p O2 2 Consideremos la reacción entre 1 mol de SO2 gaseoso a 1 atm de presión y ½ mol de O2 gaseoso a 1 atm de presión para formar una mezcla en equilibrio de SO2(g), SO3(g) y O2(g) a 1 atm de presión y 1000 K. De la estequiometría de la reacción química dada por la ecuación 10.12, x moles de SO3 son formados de la reacción de x moles de SO2 y ½ x moles de O2, y cualquier mezcla reactante contendrá x moles de SO3, (1-x) moles de SO2 y ½ (1-x) moles de O2. SO 2 inicialmen te 1 durante la reacción 1− x + 1 O 2 → SO 3 2 1 0 2 1 1 − x x 2 2 El número total de moles en el sistema nT es Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 157 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez nT = 1 − x + p SO2 = n 1 1 1 − x + x = (3 − x ) y como p i = i P luego 2 2 2 nT 2 (1 − x ) P , (3 − x ) Por lo tanto CAPÍTULO X K p2 = p O2 = 2 p SO 3 2 p SO p O2 2 (1 − x ) P , (3 − x ) = p SO3 = 2 xP (3 − x ) (3 − x ) x 2 (1 − x ) 3 P o (1 − P K p2 ) x 3 + (3 P K p2 − 3) x 2 − 3 P K p2 x + P K p2 = 0 (10.13) lo que con P=1 atm y Kp=1.876 da x = 0.463. Por lo tanto, en el equilibrio hay 0.537 moles de SO2, 0.269 moles de O2 y 0.463 moles de SO3, de modo que 2 (1 − 0.463 ) = 0.423 atm (3 − 0.463 ) (1 − 0.463 ) = 0.212 atm p O2 = (3 − 0.463 ) 2 • 0.463 = 0.365 atm p SO3 = (3 − 0.463 ) p SO2 = Para comprobar K p = 0.365 0.423 • 0.212 1 2 = 1.874 La composición de equilibrio es por lo tanto 42.3 % SO2, 21.2 % O2 y 36.5 % SO3. Efecto de la temperatura Como ∆Hº para la reacción dada en al ecuación 10.12 es negativo (-94600 J), y el principio de Le Chatelier indica que una disminución en la temperatura a presión constante desplaza el equilibrio en una dirección que involucre evolución de calor, una disminución de la temperatura a presión constante causará que el equilibrio se desplace hacia el lado del SO3. A 900 K º ∆G 900 = -14167 J ln K p = 14167 = 1,893 y por lo tanto Kp= 6.64, sustituyendo Kp= 6.64 y P= 1 atm en la 8.3144 × 900 ecuación 10.13 da x = 0.704 y entonces p SO2 = 0.258 atm, p O2 = 0.129 atm, Para comprobar K p = 0.613 0.258 • 0.129 1 2 p SO3 = 0.613 atm = 6.64 Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 158 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X La composición de equilibrio es por lo tanto 25.8 % SO2 (42.3 % a 1000 K), 12.9 % O2 (21.2 % a 1000 K) y 61.3 % SO3 (36.5 % a 1000 K). Efecto de la presión A pesar que Kp es independiente de la presión, el principio de Le Chatelier establece que un incremento en la presión total del sistema a temperatura constante desplaza el equilibrio en la dirección que involucra un descenso en el número de moles del sistema, en este caso hacia el lado del SO3. Consideremos la mezcla en equilibrio a P = 10 atm y T = 1000 K, sustituyendo P = 10 atm y Kp = 1.876 en la ecuación 10.13 da x = 0.686 en cuyo caso 2 (1 − 0.686 ) 10 = 2.714 atm (3 − 0.686 ) (1 − 0.686 ) 10 = 1.357 atm p O2 = (3 − 0.686 ) 2 • 0.686 • 10 = 5.929 atm p SO3 = (3 − 0.686 ) p SO2 = Para comprobar K p = 5.929 2.714 • 1.357 1 2 = 1.875 La composición de equilibrio es por lo tanto 27.1 % SO2 (42.3 % a 1 atm), 1.75 % O2 (21.2 % a 1 atm) y 59.29 % SO3 (36.5 % a 1 atm). Efectos de cambios en temperatura y presión Para variar simultáneamente temperatura y presión de manera ta que el número demoles de las tres especies gaseosas permanezca constante, la ecuación 10.13 indica que esta variación debe ser tal que el término P K p2 permanezca constante donde K p = e 94600 8.3144 T x − 89.37 e 8.3144 . Podemos ver que mezclando SO2 y SO3, se puede producir una mezcla de equilibrio con una presión parcial de O2 conocida. Por ejemplo, consideremos que se requiere tener una mezcla SO2(g)-SO3(g)-O2(g) a 1 atm de presión total en la cual p O2 = 0.1 atm . Para obtener esta mezcla de gases, SO3 y SO2 ambos a 1 atm de presión deben ser mezclados en la relación molar SO2/SO3= a y alcanzar el equilibrio. Si a moles de SO2 y 1 mol de SO3 se mezclan, luego de la estequiometría de la ecuación 10.12, x moles de SO3 deberán descomponerse para formar x Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 159 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X moles de SO2 y ½ x moles de O2 de modo tal que en el equilibrio, el número de moles presentes será inicialmen te a durante la reacción con n T = a + x + 1 O2 2 0 + SO 2 → SO 3 1 1 x 2 a+x 1− x 1 1 x + 1 − x = ( 2a + 2 + x ) 2 2 p O2 = En la mezcla de gases a = 4.5 x – 1. También K p2 = 2 p SO n O2 nT 3 2 p SO p O2 = P= x P lo cual para P=1 y p O2 = 0.1 atm , da 2a + 2 + x (1 − x ) 2 (2a + 2 + x ) 2 (a + x ) 2 x P A 1000K, Kp= 1.876, luego sustituyendo a en función de x y tomando K p2 =3.519 da 96.45 x3-18.709 x2 – 6.481 x = 0 o como x ≠ 0 96.45 x2-18.709 x – 6.481 = 0 de donde x = 0.374 a = (4.5 x 0.374) – 1 = 0.683 xP 0.374 = = 0.1 atm 2a + 2 + x ( 2x0.683 ) + 2 + 0.374 2 (a + x ) 2 (0.683 + 0.374 ) = = 0.565 atm p SO2 = 2a + 2 + x (2x0.683 ) + 2 + 0.374 2 (1 − x ) 2 (1 − 0.374 ) = = 0.335 atm p SO3 = 2a + 2 + x (2x0.683 ) + 2 + 0.374 p O2 = En la mezcla de equilibrio p SO2 / p SO3 = 1.7 , mientras que en la inicial p SO2 / p SO3 = a = 0.683 . Para comprobar K p = Si se hubiese 0.355 0.565 • 0.1 requerido 1 2 = 1.875 tener una p O2 = 0.212 atm , la solución de condiciones estequiométricas habría tenido a = 0, lo cual indica que SO3 puro a 1000 K y una 1 atm de presión se descompone a la misma mezcla de gases de equilibrio que la formada a partir de la mezcla inicial de 1 mol de SO2 + ½ mol de O2 a 1 atm. Por lo tanto, 0.212 atm es el máximo valor de p O2 que puede ser producido en una mezcla SO2 – SO3 a 1000 K y 1 atm de presión total. Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 160 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CAPÍTULO X 10.7. EQUILIBRIO EN MEZCLAS H2O-H2 Y CO2-CO. Estas mezclas se usan cuando se requiere fijar la presión parcial de oxígeno en valores muy bajos. Por ejemplo, si se requiere tener una atmósfera gaseosa que contenga una presión parcial de oxígeno de 10-10 atm, eso puede ser obtenido relativamente fácil estableciendo el equilibrio H2 + 1 O 2 = H2 O 2 con ∆Gº = -247500+55.85 T J De la ecuación 10.8 ln K p = 247500 55.85 − 8.3144 T 8.3144 si se requiere tener una atmósfera que contenga p O2 =10-10 atm a T= 2000K, luego a esta temperatura ln K p = 247500 55.85 − = 8.167 8.3144 x 2000 8.3144 Por lo tanto pH2O pH2 K P = 3.521 x 10 3 = p H2O 1 2 p H2 p O y con p O2 =10-10 atm 2 = 3.521 x 103 x 10 −5 = 3.521 x 10 − 2 Luego si en la mezcla de gases H2-H2O, p H2 =1 atm, la p H2O =0.0352 atm que es la presión de vapor saturada de l agua líquida a 27 ºC, y por lo tanto la mezcla de gases requerida puede producirse haciendo burbujear hidrógeno a 1 atm a través de agua líquida a 27 ºC para saturarla con su vapor. El establecimiento del equilibrio de la reacción a 2000 K da p O2 =10-10 atm en el gas. Similarmente la presión parcial de oxígeno en una atmósfera gaseosa puede ser determinada mediante la reacción CO + 1 O 2 = CO 2 2 El cambio en energía libre estándar para la reacción CO ( g) + 1 O 2( g) = C ( g) es ∆Gº = 2 111700+87.65 T J y para la reacción C ( s) + O 2( g) = CO 2( g) es ∆Gº = -394100-0.84 T J. Sumando los cambios en energía libre estándar da ∆Gº = -282400 + 86.81 T J para la reacción Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 161 Introducción a la Termodinámica de Materiales – Dra. Stella Ordoñez CO ( g) + 1 O 2( g) = CO 2( g) . Luego 2 ln K p = p O2 =10-20 atm a 1000 K, luego ln K p = Por lo tanto, K P = 1.646 x 1010 = CAPÍTULO X 282400 86.81 − , si la presión requerida es 8.3144 T 8.3144 282400 86.81 − = 23.52 8.3144 x1000 8.3144 p CO2 1 p CO p O2 2 = p CO2 p CO x 10 −10 y entonces p CO2 p CO = 1.646 Si la presión total es P = 1 atm, luego como, p CO2 + p CO =1, p CO2 = 1.646 (1 − p CO2 ) =0.622 atm y pCO= 0.378. La mezcla requerida es producida mezclando CO2 y CO en una fracción en volumen de 1.561/1, por ejemplo, 62.2 % volumen CO2 y 37.8 % volumen CO. En ambos casos la presión de oxígeno en el gas en equilibrio es tan pequeña, que las diferencias entre p CO2 p CO pH2O pH2 y en la mezcla en equilibrio y en la mezcla inicial son despreciables. La igualdad entre la fracción en volumen y la relación de presiones parciales en un gas puede demostrarse de la siguiente manera. Consideremos a cm3 de un gas A a 1 atm de presión y b cm3 de un gas B a 1 atm de presión que son mezclados a presión constante (y por lo tanto a volumen constante a+b). El número de moles de A = nA = (1xa)/R T = a/R T y el número de moles de B = nB = (1xb)/R T =b/R T. Por lo tanto en la mezcla n R T nA R T n R T nB R T = y pB = B = pA = A V (a + b ) V (a + b ) p A n A a % vol A = = = pB nB b % vol B Universidad de Santiago de Chile – Departamento de Ingeniería Metalúrgica 162