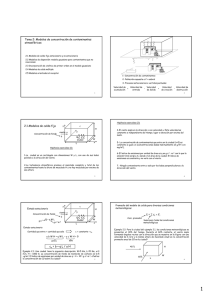
Tema 2: Modelos de concentración de contaminantes atmosféricos
Anuncio

2.1 Introducción a los modelos de concentración y tipos principales
Tema 2: Modelos de concentración de
contaminantes atmosféricos
Son protocolos matemáticos que proporcionan estimaciones
de concentración de contaminante en función de una serie de
parámetros meteorológicos, químicos, topográficos y de
cantidad y velocidad de emisión.
2.1 Introducción a los modelos de concentración y tipos principales
2.2 Estabilidad y turbulencia atmosférica: fundamentos
2.3 Modelos de celda fija estacionaria y no estacionaria
2.4 Modelos de dispersión: modelo gaussiano para contaminantes que no
reaccionan
2.5 Modelos sofisticados
2.5.1 Refinamientos del modelo gaussiano
2.5.2 Incorporación de cinética de reacción
PARÁMETROS DE
ENTRADA:
2.5.3. Modelos de celda múltiple
• Cantidad de contaminante emitida por unidad de
tiempo. Posición y altura de emisión.
• Velocidad y dirección de los vientos dominantes.
Estabilidad atmosférica. Altura de mezclado.
1
• Comportamiento químico del contaminante:
posibles reacciones, vida media.
Tipos principales
2
Fundamento básico
MODELOS DE CELDA
FIJA
Todos los modelos de concentración están basados en balances de
materia en el interior de un determinado volumen de aire:
(vertidos homogéneos)
MODELOS
GAUSSIANOS DE
DISPERSIÓN
(vertidos puntuales)
z
Velocidad de
Velocidad de
Velocidad
=
acumulación
entrada
de Salida
MODELOS
COMBINADOS
(celda múltiple, etc..)
x
y
3
2.1 Estabilidad y turbulencia atmosférica: fundamentos
+
Velocidad
Velocidad de
de creación
destrucción
Variación (derivada) de concentración de
contaminante con respecto al tiempo
4
Gradiente adiabático:
ascenso de una masa de aire seco en ausencia de transferencias de calor
Gradientes de temperatura
con el aire circundante.
Esquema simple:
• Es un proceso isoentrópico (no
hay transferencia de calor, ds = 0)
Termodinámica: dH = n CpdT = TdS + Vdp
1.
El aire caliente es menos denso y tiende a ascender.
2.
Un ascenso de aire caliente produce una expansión del gas,
porque la presión disminuye con la altura.
3.
La expansión del gas se hace a costa de su energía interna: el
aire se enfría:
n Cp dT = V dP
(proceso adiabático)
dP=ρgdz
Gradiente adiabático del aire: λ = d T / d z = g M / Cp
“entalpía” perdida: d H = n Cp dT
Ejercicio. Estimar el gradiente adiabático de aire seco.
Datos: M (Masa molecular promedio del aire) = 29 g/mol,
Calor específico molar a presión constante
Cp (calor específico a presión constante del aire) = 7/2 R
5
6
1
Inversiones térmicas
Estabilidad atmosférica
Representan la situación de máxima estabilidad, en la que el gradiente real de
temperaturas es positivo (la temperatura aumenta con la altura)
La existencia o no de corrientes verticales (atmósfera estable o
inestable) se deduce de la comparación entre el gradiente adiabático
(variación de temperatura de una masa ascendente de aire) y el
gradiente real de temperatura (aire circundante)
z
z
z
adiabático
real
adiabático
real
T
• Inversión de subsidencia: zona de altas presiones
T
T
ATMÓSFERA ESTABLE
ATMÓSFERA INESTABLE
El aire ascendente está a menos
temperatura que el circundante:
vuelve a bajar
TIPOS:
El aire ascendente está a más
temperatura que el circundante:
sigue subiendo
• Inversión por irradiación: durante la noche el aire cercano
al suelo es más frío.
• Inversión marina: cuando llega a la costa aire frío en
contacto con el agua
• Inversión topográfica: el aire frío “rellena” los valles
7
8
Clases de atmósfera según su estabilidad
Inversiones térmicas y altura de mezclado
La existencia de una zona de inversión equivale a la existencia de una
“barrera” que impide la dispersión de los contaminantes por encima de una
determinada altura. Dicha barrera determina la “altura de mezclado” (H)
Gradiente en altitud de temperaturas:
z
D
estable
inestable
z
F
Isoterma
E
C
Aire caliente
Inversión
B
Aire frío
H
A
contaminante
T
T
9
Clases de atmósfera según su estabilidad (II)
2.3 Modelos de celda fija estacionaria y no estacionaria
La clase de atmósfera viene determinada por la cantidad de insolación
(por la noche es cuando más tendencia existe a que aparezcan
inversiones). Así mismo un fuerte viento produce estabilidad vertical
Se utilizan para obtener estimaciones de concentración de
contaminante para emisiones difusas, diseminadas a lo largo de una
determinada superficie, como es el caso de una ciudad
Tabla 2.1: Clases de atmósfera según su estabilidad (Turner)
día
Viento de superficie
Radiación solar
( a 10 m) / m s-1
Fuerte moderada débil
Concentración en el interior de la ciudad
Noche, o nublado
0-2
A
2-3
3-5
5-6
C
C-D
D
D
D
≥6
C
D
D
D
D
A-B
B
A-B
B
C
E
F
B
B-C
C
D
E
Concentración de
fondo, b
-
viento: u
(concentraciones dadas
habitualmente en unidades de
masa/volumen)
11
c
z
nubes ≥ 4/8 nubes < 3/8
-
10
H
y
Q
Ciudad
L
W
x
12
2
Hipótesis esenciales del modelo de celda fija (2):
Hipótesis esenciales del modelo de celda fija (1):
1- La ciudad es un rectángulo con dimensiones W y L, con uno de sus lados
paralelo a la dirección del viento. Normalmente L se refiere a las dimensiones
de la ciudad en la dirección del viento
2- La turbulencia atmosférica produce el mezclado completo y total de los
contaminantes hasta la altura de mezclado H y no hay mezclado por encima de
esa altura. El resultado es que se puede asumir que existe una concentración
homogénea c, que es igual en todo el volumen de aire sobre la ciudad.
4- La concentración de contaminantes que entra en la ciudad (x=0) es
constante e igual a b, la llamada concentración de fondo
5- El índice de emisiones por unidad de área es q ( por ejemplo, en g s-1 ·
m-2) con lo que la emisión total es Q=q A, siendo A=WL el área de la
ciudad. El índice de emisiones es constante y no varía con el viento.
6.- Ningún contaminante entra o sale por los lados perpendiculares a la
dirección del viento.
c
z
3- El viento sopla en la dirección x con velocidad u. Esta velocidad es
constante e independiente del tiempo, lugar o elevación por encima del
suelo.
H
y
viento: u
Q
Ciudad
W
x
L
Celda fija estacionaria
Índice de emisiones:
masa por unidad
de tiempo (g s-1)
13
z
14
Celda fija estacionaria (2)
c
H
Q=qWL
El balance de materia se reduce a:
y
masa por unidad de
tiempo y unidad de
superficie (g s-1 m-2)
Q
Ciudad
ubWH+qWL–ucWH=0
W
entra
c=b+qL/uH
En el estado estacionario (la concentración no varía con el tiempo):
Velocidad de
Velocidad de
Velocidad
=
acumulación
entrada
de Salida
0
+
sale
x
L
Velocidad
Velocidad de
de creación
destrucción
0
0
Importante: la concentración es tanto más alta cuanto más larga sea
la ciudad en la dirección del viento, y además, ésta es independiente
de la anchura.
Cantidad que entra = cantidad que sale
15
Uso del modelo de celda para calcular reducción de
emisiones
Promedio sobre diversas condiciones meteorológicas
c = Σi ci × fi
16
Frecuencia en la que
se produce cada
condición
meteorológica
Conc. promedio
Problema práctico: Si para unas condiciones dadas un determinado nivel de
emisión conduce a una concentración fija de equilibrio, ¿cuál ha de ser el nivel
de emisión para conseguir una concentración dada?
q1
c1
q1 = (c1-b) u H / L
¿q2?
c2
q2 = (c2-b) u H / L
Suma para todas las condiciones
meteorológicas
q2 = q1 (c2-b)/(c1-b)
17
18
3
c
z
Modelo de celda no estacionaria
Modelo de celda no estacionaria (2)
H
y
viento: u
L/u dc/dt = b + q L / (H u) - c
Concentración de
fondo, b
Q
Ciudad
W
L/u dc/dt = ce - c
x
L
(Ecuación diferencial de 1er orden)
En el estado no estacionario la
concentración puede variar con el tiempo:
Solución:
Cantidad que entra - cantidad que sale = cantidad que se acumula por
unidad de tiempo
( ce- c(t) ) / ( ce - b) = e-u/L t
u b W H + q W L - c u W H = W H L dc/dt
entra
sale
se acumula
19
20
Formación de “penachos”
2.4 Modelos de dispersión: Modelo gaussiano
para contaminantes que no reaccionan
La combinación de la “fuerza” de emisión, la velocidad del viento y la
turbulencia atmosférica da lugar a la formación de una estructura
característica, que se denomina “penacho” (“plume” en inglés)
Son los que se utilizan para estimar la concentración de
contaminante producida por una fuente puntual, por ejemplo, la
chimenea de una fábrica, o el escape de un depósito
Dirección del viento
Momento inicial
+
flotación
Objetivo: ¿cuál es la concentración a cierta distancia de la fuente?
21
Penachos según estabilidad atmosférica
22
Penachos según estabilidad atmosférica (2)
Atmósfera neutra
Capa superior neutra,
capa inferior estable
Atmósfera inestable
(la turbulencia vertical deforma el
flujo de humo)
Capa superior estable,
capa inferior neutra
Atmósfera estable
(el flujo de humo no se dispersa)
23
24
4
Sea en un caso u en otro, el modelo gaussiano corresponde a un promedio
Nomenclatura del modelo gaussiano:
sobre cierto intervalo de tiempo:
z
Instantáneo (unos segundos)
aire contaminado
Promedio (1/2 - 1 h)
Objetivo del modelo:
∆h
y
¿ Cuál es la
concentración en un
un punto (x,y,z)?
H
h
x
dirección del viento
Además, estos son útiles para distancias de hasta 20 Km. No sirven para
problemas como la lluvia ácida, que implican cientos de Km.
25
26
Deducción del modelo gaussiano:
Fundamento del modelo gaussiano:
Para separar adecuadamente la influencia de ambos factores (viento y
turbulencia), consideraremos una caja de volumen ∆x ∆y ∆z que se mueve
con el viento:
El modelo considera que el transporte del contaminante se
produce por dos causas en principio independientes:
C
Por el viento
∆z
viento: u
Por la turbulencia atmosférica
∆y
∆x
(de esta forma todos los flujos de
SIN VIENTO
SIN TURBULENCIA
entrada y salida en la caja serán
debidos únicamente a la turbulencia)
x
Balance de materia
en la caja:
Velocidad de
=
acumulación
de
Flujos de
Σ Flujos
entrada Σ salida
Variación de masa de contaminante por unidad de tiempo (gr s-1)
27
28
Efecto de la turbulencia: teoría de la difusión
Difusión en una dimensión:
1D
El flujo viene dado por la Ley de Fick, o primera ley de la difusión:
Flujo = − K
Flujo = − K
∂c
∂x
=
masa
Balance de materia:
Área × tiempo
∂ c [( flujo )x − ( flujo )x + ∆x ]
∂ 2c
=
=K 2
∂t
∆x
∂x
“El flujo de materia a través de una pared (cantidad de masa por unidad
de superficie y unidad de tiempo) es proporcional al gradiente de
concentración, cambiado de signo, a través de la pared”
Cte de proporcionalidad
∂c
∂x
Masa depositada (t = 0)
K : constante de dispersión turbulenta
Nota: La ley de Fick fue propuesta originalmente para “difusión molecular”. En la
atmósfera la dispersión de los contaminantes se produce por turbulencia, en lugar
de por difusión, pero es una buena aproximación suponer que la forma matemática
que regula este proceso es la misma.
29
c=
M
2 (π t )
1/ 2
K
1/ 2
e
1 x2
−
4 t K
30
5
¿Por qué se llama modelo gaussiano?
M=
Normalmente, el modelo de dispersión se expresa en términos de un coeficiente
de dispersión en lugar de en la constante de dispersión turbulenta:
σ = (2Kt )1/ 2
c
c=
M
(2 π )1/ 2 σ
−
e
x2
2σ 2
σ
(concentración en masa/longitud)
X=0
31
x
32
1D
El coeficiente de
dispersión se mide en
metros y mide cuánto
se ha dispersado la
masa inicial a cada
tiempo t
2D
3D
X/metros
33
Generalización del modelo gaussiano a
tres dimensiones
∆x
Aplicaciones del modelo gaussiano al problema de la dispersión de
contaminantes en aire
∆z
∆y
∆x
∆z
34
En tres dimensiones: vertidos puntuales e instantáneos
Balance de materia aplicado en las tres
direcciones del espacio:
P. Ej. : escapes, emisiones discontinuas, etc...
∆y
Análogamente
se obtiene
En dos dimensiones: vertidos puntuales y continuados en el tiempo
∆z
∆x
∆z
∆x
P. Ej. : chimeneas en industrias, escapes continuados, etc...
∆y
∆y
c=
M
(2 π ) σ xσ yσ z
3/ 2
e
x2
−
2
2σ x
e
y2
−
2σ y2
2
− z
2σ 2
z
e
En una dimensión: vertidos puntuales y continuados en el
tiempo con mezclado total en una dirección
P. Ej. : chimeneas en industrias con baja altura de mezclado
(concentración en masa/volumen)
35
36
6
Ejemplo: desastre de Bhopal
Vertido puntual instantáneo en 3D
3 de Diciembre de 1984
C
Vertido: 45 toneladas de
Isocianato de metilo en
un segundo a una altura
de 50 metros
Se aplica al problema en el que una
determinada masa de contaminante M
es vertida súbitamente a tiempo t = 0
H
x0
El centro del vertido se mueve en
la dirección x con la velocidad
del viento u
x
Condiciones
• viento del noroeste de
fuerza 1 m/s
x0 = ut
• noche: Kx=Ky=0.45 m2s-1,
Kz=0.20 m2s-1
c=
M
(2 π ) σ xσ yσ z
3/ 2
e
( x − x0 ) 2
−
2
2σ x
e
y2
z2
−
2σ 2 − 2σ 2
y
z
(σ = (2Kt ) )
1/ 2
e
¿Concentración de
isocianato?
37
38
Ejemplo: desastre de Bhopal (2)
Vertido continuado en el tiempo: modelo en 2D
Concentración de isocianato en la estación (a 1 kilómetro en la
dirección noroeste-sureste) en función del tiempo:
Se aplica al problema en el que una cierta cantidad de contaminante es
vertida de manera constante a lo largo del eje en el que sopla el viento
0.000009
H
0.000008
0.000007
0.000006
0.000005
0.000004
0.000003
0.000002
0.000001
0
-100
-0.000001
200
500
800
1100
1400
1700
Dispersión en altura (eje z)
2000
Dispersión en la dirección perpendicular al viento (eje40y)
39
Modelo gaussiano para penacho
Vertido continuado en el tiempo: modelo en 2D (II)
¿Cuánta masa se deposita en eje x por
unidad de longitud?
(depende la
velocidad del
viento)
M = Q/u
Dispersión horizontal (eje y) y vertical (eje z)
2 DIMENSIONES:
c=
M
(2 π )σ yσ z
e
y2
−
2σ y2
2
− z
2σ 2
z
e
M=Q/u
Q: índice de emisión (masa/tiempo)
u : velocidad del viento (longitud/tiempo)
(masa depositada por
unidad de longitud)
zz-H
¿Dónde se deposita la masa?
y2
Se deposita a una altura H (altura efectiva de emisión)
c=
Reemplazo z por z – H en el modelo gaussiano
41
−
−
Q
2σ 2
e y e
2π u σ y σ z
( z − H )2
2σ z2
42
7
Coeficientes de dispersión para el
modelo gaussiano en 2D
Necesitamos un coeficiente de dispersión en el eje y y en el eje z
σ y = (2 K y t )1/ 2 = (2 K y x / u )1/ 2 = (2 K y u )1/ 2 x1/ 2
σ z = (2 K z t )1/ 2 = (2 K z x / u )1/ 2 = (2 K z u )1/ 2 x1/ 2
Los coeficientes de dispersión dependen de la distancia a
la fuente x y de las condiciones atmosféricas (K/u)
43
Determinación de los coeficientes de dispersión en
función de la distancia a la fuente (dirección y):
Condiciones
atmosféricas
A
10000
B
44
Determinación de los coeficientes de dispersión en
función de la distancia a la fuente (dirección z):
C
A
5000
D
B
C
E
F
D
1000
1000
¡ Gráfica
aproximada !
σy / m
¡ Gráfica
aproximada !
E
Consultar manuales
Consultar manuales
σz / m
100
100
10
10
F
1
3
0.1
1
10
0.1
100
X / Km
1
10
100
X / Km
45
46
Modificaciones del modelo gausiano
Z
Determinación de los coeficientes de dispersión en función de la
distancia a la fuente
Contaminante absorbido por el suelo
Ej: SO2, NOx
Fórmulas para los coeficientes de dispersión para suelos urbanos
Estabilidad
σy
σz
A-B
0.32 x ( 1 + 0.0004 x)-1/2
0.24 x ( 1 + 0.0001 x)-1/2
y2
(z− H )2
x
− 2
−
Q
2σ
c=
e y e
2 π u σ y σz
C1
Contaminante reflejado por el suelo
2 σ 2z
Z
C
0.22 x ( 1 + 0.0004 x)-1/2
D
0.16 x ( 1 + 0.0004
x)-1/2
0.11 x ( 1 + 0.0004
x)-1/2
E-F
0.20 x
0.14 x ( 1 + 0.0003
x)-1/2
0.08 x ( 1 + 0.0015
x)-1/2
Ej: CO, COVs
Generalmente:
c=
C2
σy (urbano) > σy (rural)
σz (urbano) > σz (rural)
y
( z+ H )
− 2 − ( z− H )
−
2
2
Q
2σ
e y e 2 σ z + e 2 σ z
2 π u σ y σz
2
x
47
2
2
48
8
Modelo gaussiano en 2D a ras de suelo y en el eje del viento (z = 0, y = 0):
Casos particulares del modelo gaussiano en 2D:
(Escala
logarítmica)
Contaminación a ras del suelo (z = 0):
10-3
H2
Este caso interesa por
ser donde se encuentra la
población
H=20
c u /Q m-2
y2
− 2
− 2
Q
2σ
c=
e y e 2 σz
π u σ y σz
A ras de suelo y en el eje del viento (z = 0, y = 0):
cu
1
=
e
Q π σ y σz
10-4
H=50
10-5
H=100
10-6
H2
− 2
2 σz
Este caso interesa por
ser donde se acumula la
mayor contaminación
H=300
10-7
10-8
0.1
49
1
10
100
50
X / Km
Efecto de la altura de mezclado
c
Altura L a partir de la cual no se produce más dispersión:
mezclado total en la dirección z:
Sólo se considera la
dispersión en la
dirección y
Z
σy
(Modelo gaussiano en 1D)
L
y
y=0
x
y
A partir de cierta distancia x, el contaminante
ya no se puede dispersar más en z (mezclado
total en z), y la concentración es constante a lo
largo del eje z
c=
M
(2 π ) σ y
1/ 2
El contaminante
sólo se dispersa
en la dirección y
e
y2
−
2
2σ y
Donde M = Q /(u L)
(La masa depositada M está
distribuida uniformemente
entre z=0 y z=L)
y2
−
2σ 2
Q
c=
e y
1/ 2
(2 π ) u L σ y
51
52
(Escala
logarítmica)
Efecto de la altura de mezclado (2)
Concentración
conforme al
modelo en una
dimensión
10-3
La existencia de una altura de mezcla a media altura provoca la
acumulación del contaminante y un incremento de la concentración
con respecto a la dispersión en dos dimensiones.
c u /Q m-2
H=20
Altura de mezclado
Ver siguiente
diapositiva
10-4
Altura de
mezclado
H=50
10-5
L=100
L=300
10-6
H=100
L
H=300
L=1000
10-7
contaminante
10-8
0.1
53
Líneas
obtenidas
para y=0
L=2000
1
10
X / Km
100
54
9
Resumen modelos gaussianos
Resumen modelos gaussianos
( c siempre ha de salir en unidades de masa / volumen )
( c siempre ha de salir en unidades de masa / volumen )
1 DIMENSIÓN:
c=
M
(2 π ) σ y
1/ 2
Dispersión horizontal (eje y) únicamente
e
y2
−
2σ 2
y
Dispersión horizontal (eje y) y vertical (eje z)
2 DIMENSIONES:
c=
M=Q/uL
(masa depositada por
unidad de superficie)
M
(2 π )σ yσ z
e
y2
z2
−
2 −
2
2σ y
2σ z
e
M=Q/u
(masa depositada por
unidad de longitud)
zz-H
y2
y2
−
2σ 2
Q
c=
e y
1/ 2
(2 π ) u L σ y
−
−
Q
2σ 2
c=
e y e
2π u σ y σ z
( z − H )2
2σ z2
55
56
Resumen modelos gaussianos
Ascenso de la columna de humo (ascenso vertical)
( c siempre ha de salir en unidades de masa / volumen )
Dispersión en las 3 direcciones del espacio
3 DIMENSIÓNES
M
(2 π )3/ 2 σ xσ yσ z
• momento inicial (velocidad)
• diferencia de temperatura (aire
caliente es menos denso)
h
masa depositada en un
instante dado
c=
El humo asciende debido a:
∆h
e
x2
−
2
2σ x
e
y2
−
2σ 2
y
2
− z
2σ 2
z
e
Fórmula de Holland:
∆h = Vs D / u { 1.5 + 2.68 × 10-3 P D (Ts-Ta)/Ts } (en metros)
Vs = velocidad de salida del gas en m/s
D = diámetro de la chimenea en m
Coeficientes de dispersión
que dependen de la distancia
a la fuente y la velocidad del
viento
σ = (2 K x /
u = velocidad del viento en m/s
P = presión en milibares
Ts = temperatura de la chimenea en K
u)1/2
57
Cuando la fuente
se encuentra sobre
un edificio, ésta
debe
tener
una
altura
suficiente
con
respecto
al
tejado del edificio
para
evitar
la
dispersión del humo
hacia el suelo.
2.5.1 Refinamientos del modelo gaussiano
⇒ Uso del modelo gausiano para efectos a largo plazo
Cuando se necesita una estimación a largo plazo, se realiza
un promedio sobre todas las condiciones atmosféricas,
fuentes y direcciones del viento:
∑
58
⇒ Efecto de los edificios en una columna de humo
2.5 Modelos sofisticados
c (x , y, z ) = ∑
Ta = temperatura atmosférica en K
El criterio recomendado
indica que, como mínimo,
la altura de la chimenea
ha de ser al menos una
vez y media la del edificio
∑ Frecuencia i × ci (x , y, z )
viento estabilida d fuentes
atmosféric a
59
60
10
2.5.2 Incorporación de cinética de reacción en el modelo
gaussiano
Cinética de primer order:
dC / dt = -k C → C/C0 = e-kt
En muchas ocasiones el
contaminante emitido no es
estable en aire y sufre una
reacción química que lo hace
transformarse en otra
sustancia.
Tiempo de vida media: t1/2 = ln 2 / k = 0.693 / k
Factor de destrucción/desintegración (f):
PROCEDIMIENTO
C = Cgaus * f
1.
Se calcula la concentración con el modelo gaussiano en una posición
dada.
2.
Se establece cuánto tiempo tardará la molécula en llegar hasta
dicha posición desde la fuente (velocidad del viento)
3.
Se multiplica la concentración por un factor de desintegración que
tiene en cuenta cómo decae la cantidad de contaminante con el
tiempo
f = exp(-0.693 t / t1/2) = exp(-0.693 x / u t1/2)
61
62
2.5.3 Modelos de celda múltiple
Protocolo de cálculo
Dividen el volumen total de aire
en pequeñas celdas en las que se
almacena, de manera numérica, las
concentraciones de varios
contaminantes
El modelo tiene en cuenta las
reacciones químicas sufridas por los
contaminantes (vidas medias,
constantes de velocidad) así como
los flujos de materia que pasan de
una celda a sus vecinas
63
x
y
Insolación
(intensidad de
luz, nubes)
Condiciones atmosféricas,
(vientos, humedad)
Emisiones
Concentraciones iniciales (t=0)
t = t + ∆t
Son los que se utilizan en la
práctica para estimar
concentraciones de contaminante en
regiones definidas (ciudades, por
ejemplo)
z
3- Cálculo de la dispersión
4- Cinética química
(modelos gaussianos)
(constantes de velocidad)
5- Nuevas concentraciones
64
50
0.50
HC + SOx + NOx → PM
NO
0.40
40
30
0.30
NO2
O3
20
0.20
0.10
0
24
Obtención de modelos de dispersión
Agencia de protección del medio ambiente (EPA)
http://www.epa.gov/ttn/scram
10
CO
03
Concentración de CO / ppm
Concentración de NO, NO2 y O3 / ppm
NO + HC + O2 + h ν → NO2 + O3
06
09
12
15
18
21
0
24
65
66
Hora del día
11