Comportamiento térmico de los compuestos
Anuncio

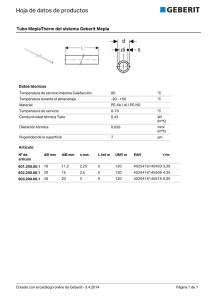
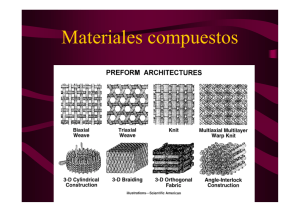
MATERIALES COMPUESTOS Capítulo 10: Comportamiento térmico de los compuestos • Tensiones térmicas y coeficientes de dilatación – – – – • Creep – – – • Tensiones y deformaciones térmicas Coeficientes de dilatación térmica Ciclado térmico de compuestos unidireccionales Ciclado térmico de compuestos laminados Bases del comportamiento de fibras y matriz Creep axial de compuestos de fibra larga Creep transversal y compuestos reforzados por fibra corta Conductividad térmica – – – Mecanismos de transmisión del calor Conductividad térmica de los compuestos Resistencia térmica de la intercara MATERIALES COMPUESTOS Tensiones térmicas y coeficientes de dilatación Tensiones y deformaciones térmicas • Proceden de la diferencia de • • poliéster vidrio 50 Tensión (MPa) • coeficientes de dilatación térmica de fibras y de matriz Lo normal será que: αf < αm en ese caso, la fibra está comprimida y la matriz traccionada Afectan a la tensión de agrietamiento de la matriz; habitualmente, reducen su valor Se relajan al incrementarse la temperatura y acercarse a la de producción Radial y circunferencial 0 Axial Circunferencial -50 Radial Axial -100 -150 0 2 4 Distancia radial (µm) 6 MATERIALES COMPUESTOS Coeficientes de dilatación térmica • El coeficiente de dilatación térmica axial se puede estimar a partir del modelo de bloques: α ax c = • 2 1 α mVm Em + α f V f E f Vm Vm Em + V f E f Vf obteniendose resultados bastante aproximados Para el coeficiente transversal, se puede utilizar la expresión propuesta por Schapery (1968): ( 1 3 αm αf Calentamiento ∆T α m ∆T Expansiones térmicas naturales ) α trc = α mVm (1 + ν m ) + α f V f 1 + ν f − α ax c ν12 c donde ν12c se obtiene a partir de la regla de mezclas de los de los componentes Compatibilidad de desplazamientos Expansion térmica real, con tensiones residuales α f ∆T εf εm σm σm αc ∆T MATERIALES COMPUESTOS Ciclado térmico de compuestos unidireccionales • Pueden aparecer tensiones importantes al variar la temperatura • Es muy importante estudiar este fenómeno, dado que tiene lugar durante el uso • del material en muchas aplicaciones y puede llevar aparejado el abandono del régimen elástico Supuesto comportamiento elástico de las fibras y que no se despegue la intercara, la deformación axial de las fibras debe coincidir con la del compuesto, luego: ( ) • σ1 f − ν f σ 2 f + σ 3 f ε1c = ε1 f = α f ∆T + Ef Como las tensiones radial y transversal serán relativamente pequeñas comparadas con la axial, se puede despreciar su efecto, con lo que la tensión en la matriz se puede obtener a partir de un equilibrio de fuerzas: • Vf E f α f ∆T − ε1c σ1 m = Si se conoce una temperatura a laVque la matriz se halla libre de tensión (vg: la de m fabricación, transición vítrea…), se puede estimar la tensión residual en la matriz y, por tanto, predecir si ésta se ha agrietado o ha fluido plásticamente ( ) MATERIALES COMPUESTOS Ciclado térmico de compuestos laminados • Los problemas asociados al ciclado térmico son aún mayores para los laminados, • • • ya que no sólo aparecen tensiones residuales entre fibra y matriz, sino también entre capas Habitualmente, el coeficiente de dilatación térmica axial es mucho menor que el transversal, con lo que las diferentes capas del laminado se constriñen mutuamente su dilatación, dando como efecto positivo una menor variación de dimensiones, a costa de mayores tensiones y la posible aparición de alabeos Para el caso de un laminado cruzado, se podrían calcular las tensiones utilizando el modelo de los bloques, como si fuera un unidireccional con la capa axial actuando como “fibras” y la transversal como “matriz”; en ese caso, tendríamos: − E1 ( α 2 − α1 ) ∆T − E1 E2 ( α 2 − α1 ) ∆T ε2 = ⇒ σ2 = E1 + E2 E1 + E2 supuesto que ambas capas tengan el mismo espesor Es muy fácil que, para diferencias térmicas relativamente pequeñas (100º C); se puedan alcanzar niveles de tensión del orden del valor de σ2u, apareciendo grietas paralelas a las fibras MATERIALES COMPUESTOS Creep Bases del comportamiento de fibras y matriz • • • • • Creep (fluencia lenta) es el término que define la deformación progresiva de un material en el tiempo, al aplicar una carga constante Puede aparecer bajo cargas reducidas (vg: 10 MPa), a temperaturas del orden del 40-50 % de la de fusión (en K) Para las resinas termoestables, unos 100º de incremento sobre la temperatura ambiente pueden provocar este fenómeno; en los termoplásticos, se puede producir, incluso, a temperatura ambiente El interés suele centarse en determinar la velocidad de deformación en el estado secundario Uno de los mayores atractivos de los compuestos, especialmente en MMC y matrices termoplásticas es, precisamente, mejorar el comportamiento frente al creep de la matriz MATERIALES COMPUESTOS Creep axial de compuestos de fibra larga • La deformación inicial, al cargar el compuesto será: ε0 = • Al fluir la matriz, las fibras van soportando cada vez más carga, con lo que, en la σc situación límite: ε = ∞ • • σc V f E f + Vm Em Vf Ef la deformación real se aproxima a este valor de forma asintótica Resulta muy interesante conocer este valor límite de la deformación bajo creep, que no será superada salvo que las fibras rompan. Además esta deformación no suele ser demasiado grande Se puede predecir la velocidad de deformación con la que el material se aproxima a la deformación límite. Si la matriz sigue una ley potencial del tipo d ε = A σ cn dt n n ε dε Aσ c 1 − ε ∞ = entonces, la velocidad de fluencia dt Vf Ef n del compuesto será (McLean, 1983): 1 + V E Vm m m MATERIALES COMPUESTOS Creep transversal y compuestos reforzados por fibra corta • • • • En el creep transversal de un compuesto de fibra larga, el comportamiento viene determinado fundamentalmente por el de la matriz Lo mismo ocurre en compuestos reforzados por particulas o fibra corta; sin embargo, en este último caso, el comportamiento del conjunto depende así mismo de la relación de longitudes de las fibras En general, los compuestos reforzados con fibras cortas presentan un comportamiento mejor que los reforzados con partículas (hasta dos ordenes de magnitud en su velocidad de deformación) En los compuestos con refuerzo de fibra corta, la intercara juega también un papel determinante en el comportamiento global MATERIALES COMPUESTOS Conductividad térmica Mecanismos de transferencia del calor • El flujo de calor en los sólidos sigue leyes del tipo: q = −K ⋅T' • • • donde K es el coeficiente de conductividad térmica (Wm-1K-1) y T’ es el gradiente de calor La conductividad térmica de los materiales depende de la temperatura; a 0 K, el coeficiente de conductividad vale 0; al aumentar la temperatura sube rapidamente, llega a un pico y después cae lentamente Los mecanismos que permiten la transferencia de calor son, fundamentalmente, dos: la vibración de los átomos (que se transmite a sus vecinos) o el intercambio de energía a través de electrones libres En los metales, se producen ambos mecanismos (por lo que sus K son más elevadas); en los no-metales, sólo se puede transmitir calor por vibración de los átomos MATERIALES COMPUESTOS Conductividad térmica de los compuestos • La conductividad térmica de un compuesto puede ser estimada a partir del modelo de bloques; las expresiones que se obtienen para el caso axial y el transversal son, respectivamente: K 1c = V f K f + V m K m V y: K = f + V m 2c K K m f • −1 1 Vm 3 Vf Isotermas la ecuación del caso axial da buenos resultados para compuestos de fibra larga; sin embargo, la transversal produce peores aproximaciones Hatta y Taya, utilizando el modelo de Eshelby, llegaron a la siguiente expresión para la conductividad transversal: K 2c = K m + 2 ( ) q1c q1f q2c Isotermas Km K f − Km Vf q2m K m + Vm K f − K m / 2 q2f ( ) que da buenos resultados en la mayoría de los casos q1c q1m q2c MATERIALES COMPUESTOS Resistencia térmica de la intercara • La intercara presenta una cierta resistencia al paso del calor; la ley que rige esta transferencia será del tipo: qi = h ⋅ ∆ T • donde h es el coeficiente de transferencia de calor de la intercara (Wm-2K-1) Esta resistencia térmica influye en la conductividad térmica transversal de los compuestos de fibra larga; Hasselman y Johnson (1987) obtuvieron la siguiente expresión analítica: K K K K f K 2c • f f f − − 1 + + +1 Vf K m rh K m rh = Km Kf Kf Kf Kf + +1 + V f 1 − + K m rh K m rh Y para compuestos con refuerzo Kp Kp Kp Kp − − 1 + +2 +2 2V f de partículas esfericas, los K rh K rh m m mismos autores obtuvieron Kc = Km Kp Kp Kp Kp la expresión: V f 1 − + +2 +2 + K m rh K m rh