Estudio mediante dinamica caótica de un contaminante primario de

XXVIII Congreso Interamericano de Ingeniería Sanitaria y Ambiental
Cancún, México, 27 al 31 de octubre, 2002
ESTUDIO MEDIANTE DINAMICA CAÓTICA DE UN CONTAMINANTE PRIMARIO DE
LA ZMCM
Victor Hugo Almanza Veloz *
UPIBI-IPN, Laboratorio de Sistemas Dinámicos
Estudiante del cuarto año de Ingeniería Ambiental, con reconocimiento al mejor promedio
del sexto semestre del plan de estudios. Reconocimiento a la excelencia académica por
parte del CECYT No. 10. Asistencia a eventos en materia de calidad del aire (INE-CENICA)
Agustín I. Cabrera Llanos
UPIBI-IPN, Laboratorio de Sistemas Dinámicos
Dirección del autor principal (*): Calle Av. Acueducto s/n, Del. Gustavo A. Madero, México D.F. –07340 – México
– Tel.57296000 ext. 57342. e-mail: mrsatanicaoss@hotmail.com
RESUMEN
Usando el método de coordenadas de retardo, se reconstruyó el atractor de una serie de tiempo de concentración del
bióxido de azufre en la ZMCM para la década 1990-2000, y se obtuvo la dimensión del mismo utilizando el
algoritmo de Grassberger y Procaccia. La serie se obtuvo de la base de datos de 15 estaciones de la Red Automática
de Monitoreo Atmosférico (RAMA), y se procesaron numéricamente en formatos: el de todos los datos registrados;
en el intervalo de las 6 a las 16 horas; y aquellos ignorando los días en que no hubo registro, con lo que se logra
establecer la reconstrucción del espacio de fase en donde se construye el atractor de las 3 estaciones más
representativas. Asimismo se obtienen características similares al mapeo de Zaslavski para los datos analizados.
Palabras Clave: atractor, dimensión, espacio de fase.
INTRODUCCION
La contaminación atmosférica es un grave problema que tiene un marcado interés tanto social como científico. A lo
largo de la historia se ha tratado de abordar el problema con el uso de herramientas como la estadística y la
modelación por citar algunas. Uno de los contaminantes primarios que forman ozono troposférico es el bióxido de
azufre, de aquí que tenga una importancia considerable en materia de calidad del aire (Compendio SEMARNAP,
2000). Las técnicas para poder analizarlo han ido evolucionando progresivamente, entre una de estas, la Teoría del
Caos no es la excepción ya que entre sus diversas aplicaciones se encuentran el área medica, económica y geofísica,
entre otras.
La mayoría de las ocasiones el uso de modelos requiere el conocimiento de las ecuaciones características que
gobiernan el fenómeno bajo estudio. Sin embargo, esto puede resultar bastante difícil cuando se quiere englobar un
mayor número de variables del fenómeno. Una alternativa de solución es el método de coordenadas de retardo, el
cual no toma en cuenta la complejidad del sistema, sino que la engloba, es decir, basta una sola variable del sistema
para la reconstrucción de la dinámica del mismo. Este método, que se basa en el uso del teorema introducido por
Takens, Ruelle y Packard (de forma independiente), establece que varias de las propiedades topológicas
fundamentales del atractor original en el espacio de estado, se conservan y pueden ser inferidas a partir del espacio
de fase reconstruido en base a las m-historias de la serie de valores observados (Ballaco, 1998) (Ott, 1993) (Packard,
1980).
Por tanto, la dinámica del sistema puede obtenerse cualitativamente calculando la dimensión del atractor a partir de
éste nuevo espacio generado empleando la dimensión de correlación.
CONTAMINACIÓN ATMOSFERICA Y EL BIOXIDO DE AZUFRE
Existen diversas definiciones de la contaminación atmosférica, una de ellas es la siguiente: ''Es la presencia en la
atmósfera exterior de uno o más contaminantes o sus combinaciones, en cantidades tales y con tal duración que sean
1
o puedan afectar la vida humana, de animales, plantas, o de la propiedad, que interfiera en el ejercicio de las
actividades''. Con esto puede aclararse el término contaminante: es polvo, vapor, niebla, líquidos, humo, otras
materias particuladas, sustancias olorosas, o cualquier combinación de las mismas. A continuación se presenta una
clasificación general de los contaminantes del aire (Warck, 1994):
1. Materia Particulada o partículas.
2. Compuestos que contienen azufre.
3. Compuestos orgánicos.
4. Compuestos que contienen nitrógeno.
5. Monóxido de carbono.
6. Compuestos halogenados.
7. Compuestos radiactivos.
De ésta lista se desprenden dos conceptos importantes: contaminante primario y contaminante secundario. El
primero es aquel que es emitido a la atmósfera por reacciones químicas entre ellos mismos y las especies químicas
usualmente encontradas en la atmósfera. Los segundos, como su nombre lo indica, proceden básicamente de los
contaminantes primarios.
Por otra parte, el bióxido de azufre (SO2) es uno de los contaminantes más habituales y representativos del aire de
nuestra ciudad. Es un gas incoloro, no flamable y no explosivo que produce una sensación gustatoria a
concentraciones de 0.3 a 1.0 ppm. A concentraciones mayores de 3 ppm, el gas tiene un olor acre e irritable.
Procede de la combustión de carbones o de aceites minerales utilizados en la producción de energía, en la industria y
en la calefacción doméstica, los cuales pueden llegar a contener azufre en una proporción de 5%. Al ser quemados
dichos combustibles, el azufre es liberado a la atmósfera en forma de dióxido de azufre o gas sulfuroso
El principal peligro que presenta el bióxido de azufre, son las reacciones químicas que bajo condiciones (humedad
ambiente), transforma el bióxido en trióxido de azufre ( SO3) ya sea por procesos fotoquímicos que por la latitud
(19º 36’ N y 19º 03’ S) recibe abundante radiación solar, o bien procesos catalíticos en la atmósfera, dando lugar al
nacimiento de aerosoles de ácido sulfúrico. Estos aerosoles son sumamente peligrosos, originando el fenómeno
conocido con el nombre de smog (término proveniente del inglés: smoke humo, y fog, niebla); y con la humedad del
aire forma ácido sulfúrico. De ahí su carácter de comportamiento primario (Warck, 1994) (Informe SEMARNAP,
2000).
De los compuestos precursores de ácidos, el SO2 en fase gaseosa es emitido en forma significativa por plantas
termoeléctricas, el cual es oxidado a SO4-2 y el radical (SO4-) al reaccionar con el peróxido de hidrógeno produce el
ácido sulfúrico influenciado por la luz solar, la humedad relativa y la presencia de nieblas y nubes. Este proceso se
describe de manera general mediante las siguientes ocho reacciones (Programa SEMARNAP, 2000).
• SO 2(g) + H 2O(l) ↔ SO 2 • H 2O
+
SO 2 • H 2O (l) ↔ H + HSO 3(l)
+
HSO3 (l) ↔ H + SO
SO
−2
3 (l)
ecuación (1)
ecuación (2)
−2
3 (l)
ecuación (3)
−
5 (l)
ecuación (4)
+ O 2 (g) → •SO
2 • SO5−(l) → •SO4−(l) + H 3O+ + •CO−3
ecuación (5)
• SO4−(l) + HCO−3 → SO4−(l)2 + H 3O + + •CO−3
ecuación (6)
• SO4−(l) + H 2O 2 → HSO4−2 + •HO2
ecuación (7)
• SO
−
4 (l)
−
−2
4
+ Cl → SO + Cl
ecuación (8)
Esto puede dar origen a la formación de lluvia ácida, la cual daña materiales de una forma drástica. Asimismo el
bióxido de azufre tiene efectos sobre la visibilidad y los materiales, y se sabe que las partículas en suspensión en la
atmósfera reducen el alcance visual al dispersar y absorber la luz.
2
METODOS DE LA TEORIA DEL CAOS
Es sabido que una serie de tiempo, es de gran ayuda cuando se persigue determinar la dinámica del sistema; por lo
que de aquí en adelante establecemos aquellas series con un tiempo discreto.
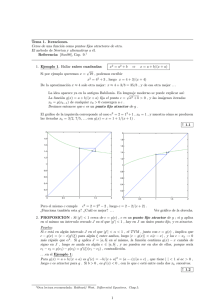
Un sistema dinámico está dado por su espacio de estado X y por su mapeo de evolución ϕ : X → X . Para un estado
inicial x 0 ∈ X en el tiempo 0, los estados sucesivos en el tiempo 1, 2, etc., están dados por x1 = ϕ ( x 0 ) ,
x 2 = ϕ 2 ( x 0 ) , etc. Con el objeto de hacer notar el concepto de serie de tiempo, Takens (1985) y Takens (1993),
propone que existe una función f : X → ℜ , que asigna a cada estado x ∈ X el valor f (x) ∈ ℜ y que puede ser
registrado o medido cuando el sistema está en el estado x . Así, para el estado inicial x 0 se obtiene la serie de
tiempo {y n = f (ϕ n (x 0 ))} (Takens, 1993). La secuencia de estados sucesivos {ϕ n (x 0 )} se conoce como la evolución del
sistema dinámico. Los diferentes tipos de evolución se mencionan a continuación: evoluciones estacionarias,
evoluciones periódicas, evoluciones cuasiperiódicas y evoluciones caóticas (en donde los atractores extraños son
distintivos de éste caso). Generalmente, el tipo de evolución es el mismo que corresponde a la serie de tiempo. Esto
es consecuencia de un resultado más general, a menudo referido como el teorema de reconstrucción (Packard, 1980)
(Sauer, 1991) (Sauer, 1993) (Takens, 1985) (Takens, 1993).
Retomando lo anterior, puede decirse que para un sistema dinámico en un espacio de estado X , el cual se asume
que sea un espacio vectorial de dimensión finita, dado por un operador en al evolución ϕ : X → X y una función
se
definen
los
mapas
de
reconstrucción
por
f : X → ℜ;
Mrk : X → ℜ k
(
(
))
Mrk (x ) = f (x ), f (ϕ ( x )), L , f ϕ k −1 (x ) ∈ ℜ k . Además, el teorema establece que pares genéricos (ϕ , f ) , Mrk define
una inserción de X en ℜ en donde k > 2 ⋅ dim( X ) . Esto significa que para una k el estado x se determina
completamente por Mrk (Sauer, 1993). Entonces, esto nos ayuda a inferir la información del espacio de estado
k
original.
Ruelle también consideró de forma similar el método propuesto por Takens (Roux, 1981) (Sauer, 1993). El asume
que una cantidad x del proceso puede ser medida en tiempos igualmente espaciados, arrojando en consecuencia
una serie de tiempo escalar x t . La sugerencia que plantea es representar el espacio desconocido E en el tiempo t
[
]
por el vector de coordenadas de retardo: b = x t , x t −τ , K , x t − (m −1)τ ; y que posee la misma característica que el
anterior: encontrar la dinámica del sistema estudiando el atractor reconstruido. Él propone lo siguiente: si m es la
dimensión de inserción y n la dimensión del atractor reconstruido, entonces m ≥2n+1. Así sobre la base del vector
de retardo, pueden formarse los vectores del espacio de fase del atractor reconstruido:
x(t) = [x(t), x(t − τ), x(t − (m − 1)τ ]
ecuación (9)
donde m es la dimensión de inserción y τ es el tiempo de retardo. Es de sobra decir, que la selección de los mismos
es de capital importancia para los resultados obtenidos. Aquí m equivale a k en la sintaxis matemática anterior, y
significa el número de ejes ortogonales en los cuales se graficará el espacio de fase a partir de la variable observada,
que en éste caso es la concentración en aire del bióxido de azufre.
Por otra parte, el cálculo de la dimensión es de fundamental interés, debido a que nos indica de una forma cualitativa
si la dinámica del sistema bajo estudio obedece a un comportamiento caótico; en donde lo anterior se justifica si la
dimensión obtenida es fraccionaria. Existen métodos para estimar aquella tales como la dimensión de Haussdorf, la
dimensión de información, o la dimensión de Lyapunov entre otros (Grassberger y Procaccia, 1983). Sin embargo,
existe un método relativamente sencillo conocido como el algoritmo de Grassberger y Procaccia.
Este último se obtiene de la correlación entre puntos aleatorios del atractor, los cuales pueden obtenerse de una serie
de tiempo. Se establece que debido a la divergencia exponencial de trayectorias, muchos pares de puntos xi , x j
(
)
con i ≠ j , serán dinámicamente pares de puntos aleatorios no correlacionados. Los puntos recaen en el atractor, sin
embargo son espacialmente correlacionados, y ésta propiedad puede medirse con la siguiente expresión:
1
C (r ) = lim 2 × número de pares (i, j ) cuya dis tan cia xi − x j es menor que r
N →∞ N
{
}
3
la cual corresponde a la integral de correlación y que se relaciona con la función de correlación
l
1
N
c(l ) = lim 2 ∑i , j =1δ F (xi − x j − l ) ∀i ≠ j , por C (r ) = ∫ d F lc(l ) . Para efecto de éste escrito se considerará la
N →∞ N
0
expresión que resulta de simplificar las anteriores, debido a que el análisis matemático es extenso y rebasa el
propósito de éste artículo. Así, se tiene (Grassberger y Procaccia, 1983) (Kantz, 1997):
(
)
N
N
ecuación (10)
2
Θ r − xi − x j
∑
∑
N(N − 1) i =1 j=i +1
donde Θ es la función paso de Heaviside: Θ(x)=0 si x es menor o igual a cero y Θ(x)=1 si x es mayor que cero
C(r) =
OBJETIVOS
i.
ii.
iii.
Definir un área de estudio para obtener una serie de tiempo de concentración representativa usando la base
de datos de la Red Automática de Monitoreo Atmosférico.
Reconstruir el atractor para la serie de tiempo representativa por el método de coordenadas de retardo.
Calcular la dimensión del atractor por el algoritmo de Grassberger y Procaccia.
METODOLOGÍA
Los datos se obtuvieron de la base de datos de 15 estaciones de la Red Automática de Monitoreo Atmosférico
(RAMA), y se procesaron numéricamente en formatos usando el software MATLAB: el de todos los datos
registrados; en el intervalo de las 6 a las 16 horas; y aquellos ignorando los días en que no hubo registro, con lo que
se logra establecer la reconstrucción del espacio de fase en donde se obtiene el atractor de las 3 estaciones más
representativas que conforman el área de estudio aplicando el método de coordenadas de retardo. El algoritmo de
Grassberger y Procaccia se empleó para estimar la dimensión del atractor de la serie de tiempo de concentración del
bióxido de azufre en la ZMCM para la década 1990-2000.
ACTIVIDADES
Las estaciones consideradas para éste artículo fueron: Vallejo, Tacuba, ENEP-Acatlán, Azcapotzalco, Tlalnepantla,
Los Laureles, La Presa, La Villa, San Agustín, Xalostoc, Merced, Hangares, Santa Ursula, Pedregal y Cerro de la
Estrella. Las estaciones I.M.P, Cuitlahuac, Chapingo, Insurgentes, Cuajimalpa y Tlalpan no registran datos de
bióxido de azufre, Compendio SEMARNAP (2000), y las estaciones restantes no tuvieron registro por varios años.
Los datos para el intervalo de las 6-16 horas se tomaron debido a que son las horas con mayor actividad del
contaminante, Informe SEMARNAP (2000), y los datos sin tomar en cuenta los días sin registro se obtuvieron con
la elaboración de un programa numérico. Es conveniente aclarar que un dato sin registro aparece como cero en los
registros de la RAMA, y de aquí en adelante se continuará considerándolo de ese modo. Proponemos el empleo de 3
estaciones de monitoreo para definir un área de estudio; las cuales deben poseer una similitud entre la media
aritmética de la serie de tiempo, para suponer que es la concentración representativa de esa área, y por lo tanto
obtener una serie de tiempo representativa de las tres estaciones.
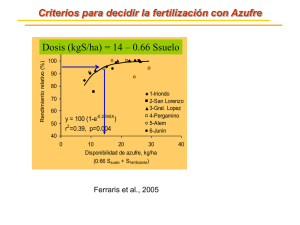
RESULTADOS
Se elaboraron los programas computacionales y se aplicaron a series de tiempo de sistemas característicos: el de
Lorenz y Rossler, Peitgen (2000), con el objeto de obtener resultados que nos aseguren la confiabilidad de los
algoritmos y poder aplicarlos a la serie de tiempo del bióxido de azufre. La siguiente figura ilustra éstos resultados:
4
a)
b)
c)
d)
Figura 1: a) y b) Atractor de Lorenz con τ = 0.05 y 0.5; c) y d) Atractor de Rossler con τ = 0.5 y 0.1
Estos resultados son satisfactorios, puesto que se observó el stretching (los puntos tienden a quedar en una
diagonal) y el folding (los puntos degeneran en una estructura doblada en si misma) del atractor para valores de τ
muy pequeños y muy grandes, comprobándose lo establecido por Grassberger (1983) y Lorenz (1963), acerca de
éstos comportamientos característicos de sistemas caóticos: la sensibilidad a las condiciones iniciales.
Después se obtuvo el área de estudio de acuerdo a las tres formas planteadas desde un principio. Respecto a la serie
de datos excluyendo los días sin registro, tuvieron que usarse solamente 74478 datos de los 96432 datos originales,
esto implica ignorar 21954 datos. Este número de datos fue el número obtenido para la estación Los Laureles. En la
tabla 1 se presentan los resultados de las tres alternativas mediante programas computacionales para las estaciones
de la RAMA.
TABLA 1. Estaciones que presentaron concentración semejante
DATOS ORIGINALES
Vallejo
0.0223
ENEP-Acatlán
0.0192
Vallejo
0.0250
La Presa
0.0202
Vallejo
0.0263
Vallejo
0.0263
Los Laureles
0.0201
Tacuba
0.0235
Azcapotzalco
Tlalnepantla
0.0225
0.0231
Hangares
Santa Ursula
0.02
0.019
DATOS DE 6-16 hrs
Azcapotzalco
Tlalnepantla
0.0243
0.0248
Hangares
Santa Ursula
0.0210
0.0206
DATOS EXCLUYENDO LOS DIAS SIN REGISTRO
Tlalnepantla
0.0264
Azcapotzalco
0.0271
Pedregal
0.0203
Hangares
0.0241
La Villa
0.0272
Tlalnepantla
0.0264
Cerro de la Estrella
0.02
Santa Ursula
0.0224
Diferencia
0.0008
0.001
Diferencia
0.0007
0.0008
Diferencia
0.0009
0.0008
0.0003
0.0017
5
En base a lo anterior se eligieron las estaciones: Los Laureles, Pedregal y Cerro de la Estrella, para representar el
área de estudio. Se efectuó un promedio para las tres, para poder obtener la serie promedio de concentración del
bióxido de azufre. Se uso la serie en cuestión para reconstruir el atractor usando (9) eligiendo un retardo de ¾ y una
dimensión de inserción de 3; así como el uso de (10) para obtener la dimensión del atractor que resultó ser
1.48±0.07. En La figura 2 se muestra el atractor reconstruido para la serie de tiempo empleada, la figura 3 es un
acercamiento del espacio de fase con el objeto de discernir un comportamiento no visible a primera instancia y la
figura 4 muestra el mapeo de Zaslavski.
Figura 2: Atractor reconstruido de la serie de tiempo promedio
Figura 3: Acercamiento del atractor
Figura 4 : Mapeo de Zaslavski
Se puede observar de éstas figuras la similitud con el mapeo de Zaslavski: las líneas que indican el comportamiento
caótico, (Grassberger, 1983) (Zaslavski, 1978). No obstante, el mapeo anterior se obtuvo con las ecuaciones que lo
describen. Por razones obligatorias, se reconstruyó el mismo a partir de una serie de tiempo generada con otro
programa computacional. Esto se muestra a continuación:
a)
b)
Figura 5: Reconstrucción del mapeo de Zaslavski, a) con τ = 0.02 y b) con τ = 3/4
Se aprecia una dinámica aceptable con parámetros similares a los experimentales. Sin embargo, como se estableció
en líneas anteriores, la dimensión del atractor nos permite establecer de una manera más certera “lo caótico de un
atractor”. Las gráficas de la figura 6 ilustran los resultados del algoritmo:
6
a)
b)
c)
d)
Figura 6: a), b) y c) Dimensión para las estaciones Laureles, Pedregal y C. Estrella; d) Dimensión promedio
En las primeras se calculó la dimensión para cada estación del área de estudio, en donde los resultados difieren de la
obtenida para el área como conjunto: Para la estación Los Laureles y Pedregal, se obtuvieron dimensiones similares:
1.6966 y 1.6982 respectivamente, y para cerro de la Estrella 1.8703. Lo anterior puede ser un indicio de un
resultado aún más interesante: que el comportamiento del bióxido de azufre tenga características de multifractalidad.
Lo anterior requiere de análisis tales como el concerniente a los exponentes de Higuchi, pero por cuestiones
contextuales no se ahondará en el mismo. Sin embargo, el resultado para la serie promedio, no implica que se haya
errado, ya que el algoritmo de Grassberger arroja resultados globales, en donde el que se obtuvo es aceptable y
confiable debido a que el mismo se aplicó a las series de sistemas anteriormente expuestos para obtener dimensiones
confiables.
CONCLUSIONES Y RECOMENDACIONES
Un enfoque dinámico ha sido efectuado en éste artículo para la serie de tiempo del bióxido de azufre en la ZMCM
para el período en cuestión. Las tres estaciones elegidas representan un área considerable, debido a que engloba la
zona noreste, sureste y suroeste, respectivamente, de la ZMCM. La reconstrucción del atractor per se muestra un
comportamiento dinámico con una densidad de puntos mayor en valores de concentración reducidos. Este hecho
coincide con estudios estadísticos para éste contaminante, Informe SEMARNAP (2000), en donde se reporta una
tendencia decayente para el mismo. Sin embargo debe aclararse que éste es un enfoque dinámico y no estadístico,
aunque se apoye en métodos de ese estilo. La coordenada de retardo se eligió de ¾, por ser la que mejor
representaba el comportamiento, puesto que se probaron los valores en el intervalo 1/100-1/12. Se decidió hacer un
acercamiento para una serie de puntos en la zona de mayor densidad de los mismos, arrojando un resultado curioso:
se asemeja bastante al mapeo de Zaslavski reportado en literatura, lo que nos hace pensar que la serie de tiempo es
caótica; pero no solamente éste hecho, sino también el concerniente a la elección de la coordenada de retardo, ya
que el fenómeno de stretching exhibe dependencia en las condiciones iniciales, una característica de sistemas
caóticos. Esto último se corrobora al obtener la dimensión del atractor mediante la pendiente de los puntos con
tendencia más lineal, la cual es fraccionaria, o fractal como también se le conoce, arrojando un valor de 1.48, que es
bastante similar al reportado para el mapeo de Zaslavski: 1.53. Lo anterior nos muestra la gran similitud entre el
mapeo de Zaslavski y el atractor reconstruido que obtuvimos, y obliga a formularse la siguiente pregunta: ¿ Podría
obtenerse una relación entre éstos resultados y el mapeo de Zaslavski ?; porque de ser así, nos mostraría un
panorama totalmente distinto: tal vez la dinámica de la concentración del bióxido de azufre en éste período no sea
tan complicada y pueda representarse mediante un mapeo sencillo. Esto implicaría obtener un modelo significativo y
relativamente sencillo de elaborar, es decir, la capacidad de cómputo requerida sea la que está al alcance de la
mayoría de las personas. Además podría complementar a estudios de dispersión al momento de elaborar inventarios
7
de emisiones. Finalmente, estudios de exponentes de Lyapunov y de Higuchi, ayudarían en una mejor
caracterización del comportamiento, y poder establecer con base en ellos, métodos de predicción e incluso
complementarlos con métodos de Redes Neurales, Lógica Difusa, Algoritmos Genéticos o combinaciones de ellos.
REFERENCIAS BIBLIOGRAFICAS
Baker G. (1998) Chaotic Dynamics: an introduction, Cambridge University Press, UK, 375 pp.
Balacco H. (1998) Señal de caos en series de tiempo financieras, en FCE, Argentina.
Compendio Estadístico de la Calidad del Aire 1986-1999. (2000) Secretaría del Medio Ambiente, México.
Grassberger P., Procaccia I. (1983) Measuring the strangeness of strange attractors; Physica, vol. 9D, 189-208.
Informe Anual de la Calidad del Aire en el Valle de México.(2000) Secretaría del Medio Ambiente, México.
Kantz H. (1997) Nonlinear time series analysis, Cambridge University Press, UK, 304 pp.
Lorenz E. (1963) Deterministic non-periodic flow; J. Atmos. Sci., vol. 20, 130-141.
Ott, E. (1993) Chaos in Dynamical Systems, Cambridge University Press, UK, 457 pp.
Packard, E. (1980) Geometry from a Time Series, Phys. Rev. Lett, vol. 45, 712-716.
Peitgen H., Jürgens H. (1992) Chaos and fractals: New Frontiers of Science, Springer-Verlag, NY, 965 pp.
Programa de Precipitación ácida en la ZMCM (2000). Secretaría del Medio Ambiente, México.
Roux J. (1981) Observation Of A Strange Attractor Phys. Rev. Lett.
Sauer T. (1993) How Many Delay Coordinates Do You Need, IJBC, vol. 3, 737.
Sauer T. (1991) Embedology, J. Stat. Phys, vol. 65, 579.
Takens F. (1985) Dynamical Systems and Bifurcations Lecture Notes in Math. Vol. 1125, Springer, Heidelberg.
Takens F.(1993) Detecting Nonlinearities in Stationary time Series, IJBC, vol. 3, 3.
Warck H. (1994) Contaminación Del Aire. Limusa. México.
Zaslavski G. (1978) The simplest case of a strange attractor Phys. Lett, vol. 69A, 145-147.
8