JUNTURA P - N - Universidad Nacional de Tucumán
Anuncio
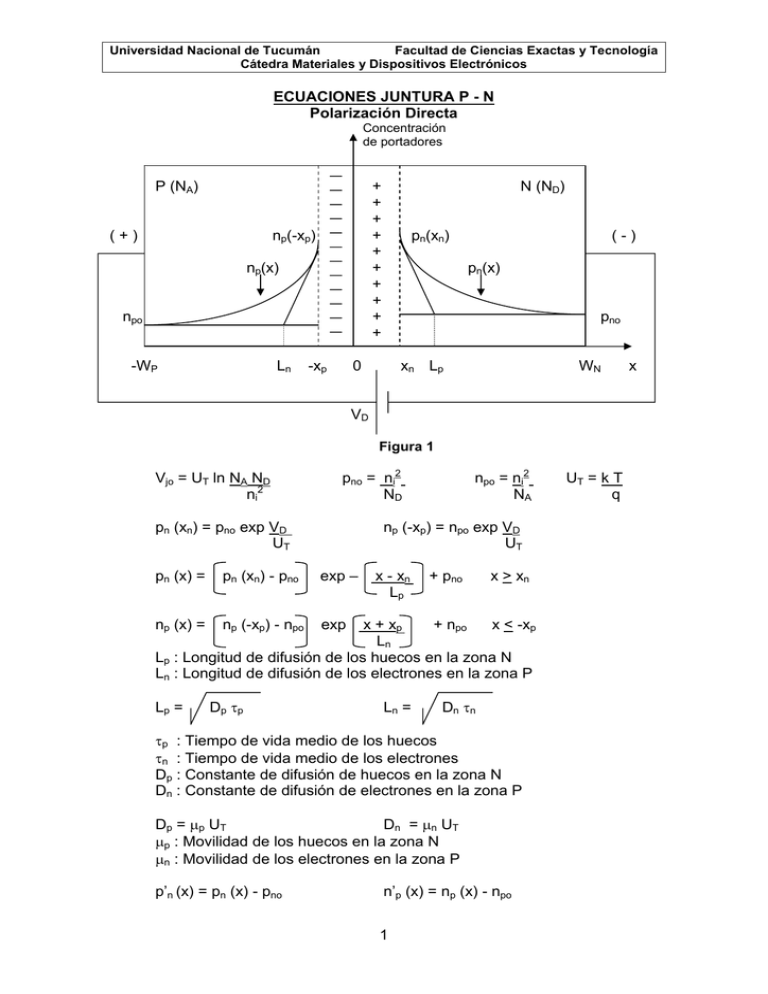
Universidad Nacional de Tucumán Facultad de Ciencias Exactas y Tecnología Cátedra Materiales y Dispositivos Electrónicos ECUACIONES JUNTURA P - N Polarización Directa Concentración de portadores P (NA) + + + + + + + + + + np(-xp) (+) np(x) npo -WP Ln -xp N (ND) pn(xn) (-) pn(x) pno 0 xn Lp WN VD Figura 1 Vjo = UT ln NA ND ni2 pno = ni2 ND pn (xn) = pno exp VD UT npo = ni2 NA np (-xp) = npo exp VD UT pn (x) = pn (xn) - pno exp – np (x) = np (-xp) - npo exp x - xn Lp + pno x > xn x + xp + npo x < -xp Ln Lp : Longitud de difusión de los huecos en la zona N Ln : Longitud de difusión de los electrones en la zona P Lp = Dp τp Ln = Dn τn τp : Tiempo de vida medio de los huecos τn : Tiempo de vida medio de los electrones Dp : Constante de difusión de huecos en la zona N Dn : Constante de difusión de electrones en la zona P Dp = μp UT Dn = μn UT μp : Movilidad de los huecos en la zona N μn : Movilidad de los electrones en la zona P p’n (x) = pn (x) - pno n’p (x) = np (x) - npo 1 UT = k T q x Universidad Nacional de Tucumán Facultad de Ciencias Exactas y Tecnología Cátedra Materiales y Dispositivos Electrónicos I (Corrientes) IT P (NA) IEp(x) IEn(x) N (ND) (+) (-) IT IDn(x) -WP IDp(x) Ln -xp 0 xn Lp WN VD Figura 2 IDp (x) = -q AE Dp dp’n(x) dx AE : Area transversal de la juntura IDp (x) = q AE Dp (pn(xn) Lp - pn0) IDn(x) = q AE Dn dn’p(x) dx exp – IDn(x) = q AE Dn (np(-xp) - np0) exp Ln x - xn Lp x + xp Ln x > xn x < -xp IT = Cte. ( No depende de x ) IT = IEn(x) + IDp(x) x > xn IT = IEp(x) + IDn(x) x < -xp IT = IEn(WN) = IEp(-WP) IEp (-xp) = IDp(xn) e IEn(xn) = IDn(-xp) si no hay recombianción entre –xp < x < xn IT en x = 0 son corrientes por difusión IT = I Dp(xn) + I Dn(-xp) IDp(xn) = q AE Dp dp’n(x) dx x = xn IDn (-xp) = -q AE Dn dn’p(x) dx x = -xp IDp (xn) = q AE Dp (pn(xn)- pn0) = q AE Dp pn0 Lp Lp IDn(-xp) = q AE Dn (np(-xp) - np0) = q AE Dn np0 Ln Ln IT =q AE Dp pn0 + Dn np0 Lp Ln exp 2 VD UT -1 exp exp VD UT VD UT -1 -1 Universidad Nacional de Tucumán Facultad de Ciencias Exactas y Tecnología Cátedra Materiales y Dispositivos Electrónicos Ecuacion del diodo ideal I = IS exp VD UT -1 IS = q AE Dp pn0 + Dn np0 Lp Ln = q AE ni2 Dp + Dn Lp ND Ln NA Juntura asimetrica Juntura P+N cuando NA >> ND IS = q AE ni2 Dp Lp ND Juntura N+P cuando ND >> NA IS = q AE ni2 Dn Ln NA En cada caso el parametro IS esta determinado por la concentracion de impurezas de la zona menos contaminada. En una juntura P+N polarizada directa, la corriente a traves de la zona de deplexion es casi exclusivamente de huecos de la zona P a la N, en la juntura N+P es casi exclusivamente de electrones que cruzan de la zona N a la P. Diodo Corto: Si WN << Lp y WP << Ln Concentración de portadores P (NA) - + - + - + - + - + N (ND) pn(xn) np(-xp) np(x) pn(x) IT pno npo -WP -xp + 0 xn VD Figura 3 3 WN x Universidad Nacional de Tucumán Facultad de Ciencias Exactas y Tecnología Cátedra Materiales y Dispositivos Electrónicos IDp(xn) = q AE Dp dp’n(x) dx IDn (-xp) = -q AE Dn dn’p(x) dx x = -xp x = xn dp’n(x) = pn(xn) - pno = cte. dx WN IDp (xn) = q AE Dp pn0 WN dn’p(x) = np(-xp) - npo = cte. dx WP exp IDn(-xp) = q AE Dn np0 WP exp IT =q AE Dp pn0 + Dn np0 WN WP IS = q AE Dp pn0 + Dn np0 WN WP VD UT -1 = IDp (x) = cte. VD UT -1 = IDn(x) = cte. exp VD UT = q AE ni2 -1 = IS exp VD UT -1 Dp + Dn WN ND WP NA Capacidad de Difusión a ) Juntura Corta - Carga almacenada en las zonas neutras con polarización directa QpN: Carga de huecos en la zona N = Area bajo pn(x) de la figura 3 QpN = ½ q AE WN p’n(x) = q AE WN pn0 2 exp VD UT -1 QnP: Carga de electrones en la zona P = Area bajo np(x) de la figura 3 QnP = ½ q AE WP n’p(x) = q AE WP npo 2 - Suponiendo una Juntura P+N I = q AE Dp pn0 exp WN VD UT -1 4 exp VD - 1 UT QnP << QpN Universidad Nacional de Tucumán Facultad de Ciencias Exactas y Tecnología Cátedra Materiales y Dispositivos Electrónicos - Tiempo de transito (TT) = QpN = W2N I 2 Dp - Q = TT I - Capacidad = dQ = TT dI = TT I dV dV UT CD = Capacidad de difusión = TT I ( Juntura corta ) UT b ) Juntura Larga P+N - Carga almacenada en las zona N con polarización directa QpN Carga de huecos en la zona N = Area bajo pn(x) de la figura 1 WN QpN = q AE WN p’n(x) dx = q AE xn ( pn(xn) – pno ) exp – ( x – xn ) dx Lp xn QpN = q AE Lp ( pn(xn) – pno ) exp – (WN – xn ) _ exp – (xn – xn ) Lp Lp exp – (WN – xn ) = 0 Lp exp – (xn – xn ) = 1 Lp QpN = q AE Lp ( pn(xn) – pno ) = q AE Lp pn0 I = q AE Dp pn0 exp VD UT Lp QpN I = exp VD UT -1 L2p = τp ( tiempo de vida medio de los huecos ) Dp Q = τp I Capacidad = dQ dV = τp dI dV = τp I UT CD = Capacidad de difusión = τp I ( Juntura larga ) UT 5 -1 Universidad Nacional de Tucumán Facultad de Ciencias Exactas y Tecnología Cátedra Materiales y Dispositivos Electrónicos JUNTURA en Polarización Inversa P N xmo -xpo xno X Polarizacion cero P N xm -xp xn X VD Polarizacion directa P N (-) xm (+) -xp xn VR Polarizacion inversa 6 X Universidad Nacional de Tucumán Facultad de Ciencias Exactas y Tecnología Cátedra Materiales y Dispositivos Electrónicos xm = xp + xn xm < xmo para polarizacion directa VD > 0 xm > xmo para polarizacion inversa VD < 0 Cj = ε AE Capacidad de juntura xm xm f(VD) Cj f(VD) xmo ε = 1,04 10 –12 F cm xm para VD = 0 Buscamos la función xm (VD ) para encontrar Cj (VD) ρ (Densidad de carga) q ND -xp xn x -q NA E (Campo Electrico) -xp xn x V (Potencial) V2 Vjo + VR V1 -xp xn xp NA = xn ND 7 x Universidad Nacional de Tucumán Facultad de Ciencias Exactas y Tecnología Cátedra Materiales y Dispositivos Electrónicos d2V = - ρ dx2 ε Ecuacion de Poisson para una dimensión d2V = - ρ = q NA dx2 ε ε para -xp < x < 0 Integrando d2V respecto a x obtengo: dx2 dV = q NA x + C1 dx ε Condicion de borde dV = 0 C1 = q NA xp dx x = -xp ε dV = q NA (x+ xp ) dx ε para -xp < x < 0 E (x) = - dV = -q NA (x+ xp ) para -xp < x < 0 dx ε |Emax| = | E ( 0 ) | = q NA xp ε Integrando dV respecto de x obtengo: dx V (x) = q NA ( x2 + x xp ) + C2 para -xp < x < 0 ε 2 Condición de borde para calcular C2: V (-xp ) = 0 V (x) = q NA ( x+ xp )2 2ε C2 = q NA x2p 2ε para -xp < x < 0 |Emax| = E ( 0 ) = q NA xp = q ND xn ε ε 2 V1 =V( x ) = q NA x p X=0 2ε Haciendo el mismo analisis para 0< x < xn V2 =V( x ) q ND x2n X= xn 2ε = V1 + V2 = Vjo + VR = Vjo – VD Vjo + VR = q ( ND x2n + NA x2p ) = q x2p NA ( NA + 1 ) = q x2n ND ( ND + 1 ) 2ε 2ε ND 2ε NA x2p = 2 ε ( Vjo + VR) q NA ( NA + 1 ) ND x2n 8 = 2ε ( Vjo + VR ) q ND ( ND + 1 ) NA Universidad Nacional de Tucumán Facultad de Ciencias Exactas y Tecnología Cátedra Materiales y Dispositivos Electrónicos Para junturas asimetricas: ½ P+N xm = xn = 2ε ( Vjo + VR ) ½ q ND ½ + NP xm = xp = 2ε ( Vjo + VR ) ½ q NA ½ |Emax| = 2q ND NA (Vjo + VR ) ε ( ND + NA ) Cj = ε AE Capacidad de juntura xm ε = 1,04 10 –12 F cm Para calcular Cj supongo una juntura asimetrica P+N xm = xn ½ Cj = ε AE 2ε q ND ½ AE 2 2 ε q ND Cj = Cjo = AE 2 2 ε q ND 1 ( Vjo + VR ) ½ = 1 ( 1+ VR ) ½ Vjo Vjo ½ Para VR = 0 p/ juntura P+N Vjo ½ Para VR = 0 Cj = Cj = Cjo = AE 2 Cjo ( 1+ VR ) ½ Vjo 9 2 ε q NA Vjo p/ juntura N+P








