caracterización actualizada de la cámara reverberante del
Anuncio

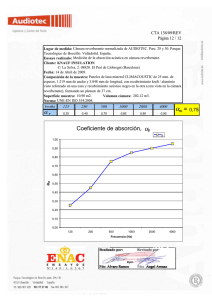
CARACTERIZACIÓN ACTUALIZADA DE LA CÁMARA REVERBERANTE DEL INSTITUTO DE ACUSTICA REFERENCIAS PACS: 43.55.Br, 43.55.Cs De la Colina, C; Rodríguez, R.M.; Simón, F.; Pfretzschner, J.; Moreno, A. Instituto de Acústica del CSIC Serrano144 28006 Madrid. España Tel: 34 915 618 806 Fax: 34 914 117 651 ABSTRACT In 1965 A. Lara et al. described, in a short publication, the main acoustic characteristics of the reverberant room of the Instituto de Acústica. Since that time some changes have significantly improved its features. In parallel, international standards dealing with precision methods on measuring sound absorption and sound power have experienced a noteworthy progress and contains new requirements to fulfil by reverberant room facilities. In this work some recent characterisations of the above mentioned reverberant room are described. Reverberation time as a function of frequency is analysed regarding UNE EN 20354 (ISO 354) standard. Normal modes and spectral densities particularly in the low frequency range are described and compared to classical polynomial approaches. Analysis of diffusion covers most recent theories and proposed metrics, by using prospections along closed trajectories and fixed points. Practical conclusions are given of interest in sound power measurements and random vibration techniques in solids excited by airborne sound. RESUMEN Aparte del interés teórico que pueda tener un campo difuso, la utilidad práctica de disponer de una buena cámara reverberante se deriva de la sencillez experimental en la medición de la absorción sonora de materiales y objetos, de la potencia acústica de fuentes sonoras y de la exploración de vibraciones aleatorias en sólidos excitados por vía aérea. Es fundamental por consiguiente alcanzar grados suficientes de aproximación a la situación ideal de difusión. Las normas internacionales de medición tratan de establecer condiciones mínimas de aproximación y se han investigado y desarrollado magnitudes de razonable fácil determinación que garanticen un adecuado cumplimiento. Lara et al. presentaron en el Congreso Internacional de Acústica, celebrado en Lieja en 1965, las características y propiedades de la cámara reverberante del Instituto de Acústica del CSIC. Desde entonces se han realizado nuevos tratamientos que han producido indudables mejoras en su comportamiento. Paralelamente las normas de medición de las distintas magnitudes medibles en estos recintos han progresado notablemente tanto en la definición como en los niveles de exigencias de las prestaciones exigibles a estos recintos. La teoría de campos acústicos difusos también ha experimentado un gran progreso y se han desarrollado y propuesto nuevas y mas fundamentadas métricas para la medida del grado de difusión de un recinto concreto. Página 1 de 7 Parece pues un buen momento para difundir las propiedades actuales de la citada cámara reverberante del IA-CSIC, a la luz del grado actual de progreso teórico y normativo. Este es el objetivo del presente trabajo. PRINCIPALES CARACTERÍSTICAS CONSTRUCTIVAS La instalación se compone de dos partes, la cámara propiamente dicha y un laboratorio de control ambos dentro de un cerramiento general de protección del ruido exterior que favorece bajos niveles de ruido de fondo. Dos de las paredes, verticales, opuestas forman un ángulo de 10º y las otras dos de 5º, con solo un diedro de 90º1). Una pared está dotada de un rectángulo retráctil, de 3.65x3 m2, realizado en palastro de acero de 15mm de espesor trasdosado con una capa de cemento de 50 mm de espesor. Figura 1. Esquema constructivo de la cámara reverberante El techo está constituido por un forjado con inclinación de 10º, a base de viguetas unidireccionales, y bovedillas de bloques de hormigón. Datos numéricos de geometrías: Base trapezoidal: 5.7 - 7.35 - 6.25 - 6.3 m Altura : 4.90 m en media (inclinación de 10º) Superficie. 210 m2 Volumen: 200 m3 El acceso se realiza a través de dos puertas enfrentadas, una en el cerramiento exterior y otra en el interior, con absorbentes de banda ancha en el contorno de la cavidad entre ambas. Complementando la geometría irregular de la cámara, se han dispuesto ocho difusores planos de metacrilato de 20 mm de espesor, con formas trapezoidales diversas y longitudes entre 1.75 m y 2 m y anchos entre 0.6 m y 1.30 m. El número, la distribución y orientación se ha conseguido siguiendo las reglas del arte usuales: estabilidad de los valores del coeficiente de absorción en las frecuencia de 100 Hz a 10 KHz, con una muestra patrón de la que somos depositarios, usada en el ASTM Sound Absorption Round Robin Test, Task Group E33.05J en la década 1970-1980. Página 2 de 7 La temperatura oscila entre unos 24ºC en verano y 15ºC en invierno. La humedad relativa varía entre 45/50 % en verano y 65/70 los periodos lluviosos, generalmente otoño y fin de invierno. TIEMPO DE REVERBERACIÓN Hay pequeñas variaciones del tiempo de reverberación de la cámara vacía, dependiendo sobre todo de la temperatura y de la humedad relativa. En la figura siguiente aparece un valor representativo para las condiciones hr = 59 %, T = 16 ºC. También aparece el valor límite inferior exigido para estas cámaras en la norma UNE EN 20354 (ISO 354). Camara Reverberante Instituto de Acústica 20 10 Tr s 5 2 1 125 250 500 1000 2000 4000 Frecuencia Hz Figura 3. Tiempos de reverberación de la cámara reverberante y tiempos exigidos por la norma UNE EN 20354 FRECUENCIAS PROPIAS Se han determinado mediante dos técnicas diferentes: barridos de tonos puros y señales impulsivas. A partir de su conocimiento se ha establecido la frecuencia de Schroeder, que limita inferiormente el rango en que se puede considerar el campo acústico difuso. Así mismo, se ha estimado el factor de solapamiento que proporciona un valor cuantitativo de la Camara Reverberante posición relativa de los modos propios del recinto. Nexp En la figura 4 se muestra el numero de frecuencias propias por debajo del valor de la frecuencia indicada en el eje de abscisas. La línea quebrada corresponde a los resultados experimentales, mientras que el trazo suave corresponde al polinomio: 4πV ⎛ f ⎞ πA ⎛ f ⎞ L f ⎜ ⎟ + ⎜ ⎟ + 3 ⎝c⎠ 4 ⎝c⎠ 8 c 3 N= N Nteor. Se han limitado los puntos de recepción a la zona en donde se colocan las muestras en estudio, lo que debe producir una disminución del numero de frecuencias propias detectado, respecto al correcto. Las excitaciones se han realizado en dos puntos. 45 40 35 30 25 20 15 10 5 0 0 50 100 150 f (Hz) 2 (1) Página 3 de 7 Figura 4. Número de frecuencias propias, teórico y experimental sustituidos los valores V (volumen), A (superficie) y L (longitud) de la cámara, indicados anteriormente. En este tipo de determinaciones directas, el solapamiento modal o cociente entre el ancho de una resonancia (Δf para las frecuencias con nivel 3 dB por debajo del máximo) y la separación media entre resonancias consecutivas, impone un límite teórico al poder de discriminación. El solapamiento crece con la frecuencia y para la cámara reverberante considerada, a la frecuencia de 100Hz se obtiene el valor 0.7, lo que indica que a esta frecuencia empiezan a distinguirse mal frecuencias de resonancia diferenciadas. De hecho, además de otras Camara Reverberante causas, este efecto es ya patente en la gráfica dNexp dNteor anterior a partir de 70/80 Hz. 12 Otra magnitud de interés es la densidad de frecuencias propias. En la figura 5 aparece una aproximación a esta magnitud tomando como intervalo diferencial de frecuencias el valor 12.5 Hz. Se compara con el valor teórico esperable para la cámara. 10 dN 8 6 4 2 La frecuencia de Schroeder, para esta cámara se sitúa en 450 Hz, a partir de la cual 0 podría considerarse que posee muy buenas 0 50 100 condiciones de difusión, y el cálculo da 14 f (Hz) frecuencias propias por Hz, en esta Figura 5. Densidad de frecuencias propias, frecuencia. Hacemos notar, no obstante, que valores teóricos y experimentales la norma EN 23741:1991 señala que la frecuencia mínima a la que se puede usar una cámara de 200 m3 es 100 Hz, lo que significa una exigencia menor que el indicado por la frecuencia de Schroeder, más próximo a condiciones ideales de difusión. CONDICIONES DE DIFUSIÓN Lo referido en el apartado anterior son aspectos parciales de la verdadera característica específica de una cámara reverberante que es el grado de difusión. Aunque el concepto de difusión es bastante claro no se han propuesto métricas adecuadas para su valoración. Una de las magnitudes más usadas ha sido la homogeneidad del nivel de presión sonora. Aunque es una condición primaria, y en sí misma no garantizaría la difusión, al introducir la teoría modal de recintos en el cálculo se ponen en juego propiedades de direccionalidad muy importantes. R. H. Lyon2) obtiene para la varianza temporal normalizada de la presión cuadrática media, en una banda de frecuencia con un número suficientemente elevado de modos propios, la expresión σ p2 m 2 2 p2 = ψ N4 x Δ2N N 2 + C NM N ,M (2) donde Ψ es la forma modal de amplitud, ΔN = C NM = PN2 t − PN2 2 N t ,N P PN PM 2 N t ,N P t t ,N es la varianza de las amplitudes es la correlación entre las amplitudes modales Página 4 de 7 (3) (4) P t es la esperanza matemática de P para el subíndice t. El propio Lyon, comparando los sistemas acústicos multirresonantes con las condiciones de máxima aleatoriedad de sistemas de partículas propone para el campo difuso ideal en una banda de frecuencia las tres condiciones siguientes: a) todos los modos propios son igualmente energéticos, b) el potencial de velocidades y la presión acústica de cada modo son independientes estadísticamente y c) la propiedad anterior se mantiene al comparar dos modos propios cualesquiera. A partir de estas definiciones propone la métrica siguiente, que denomina de regularidad del recinto R = α Δ2N N 2 + β C NM (5) N ,M en donde se ve la analogía formal con la ecuación anterior. Otro de los métodos para valorar el grado de difusión de un recinto está basado en técnicas de correlación cruzada. Muchos autores desde Dämmig3) han encontrado para la correlación cruzada entre las presiones acústicas, en campos idealmente difusos, captadas en dos puntos r y r +Δr, la expresión: C ( r , r + Δr ) = sin( kΔr ) kΔr (6) siendo Δr, la distancia entre los dos puntos Lubman4) propone la exploración del campo acústico por medio de un micrófono que describe, con velocidad angular constante, una trayectoria circular dentro del recinto, siendo la señal de excitación un tono puro. En estas condiciones se puede hacer el cambio de la variable tiempo, por la distancia, relacionadas mediante la velocidad. En general, la presión sonora varía, tanto en amplitud como en frecuencia, siendo la señal resultante un tono puro modulado en amplitud. Según el teorema de Wiener-Khintchine, la transformada de Fourier de la función de autocorrelación es la densidad espectral de potencia de la señal temporal. Como ya se ha indicado, teóricamente, en un campo acústico “perfectamente difuso”, la función de correlación espacial de la presión sonora entre dos puntos del mismo, o simplemente, la función de correlación, se define por la expresión (6). Al tratarse de un recorrido circular, con variaciones de presión con la distancia, la función de autocorrelación de la señal temporal captada puede representarse por: C (t ) = sin(k0Vt ) ⋅ cos(ω 0t ) (k0Vt ) 6a 6b 2Vf0/c Figura 6a. Señal temporal captada en la cámara reverberante, con excitación de tono puro de 500 Hz. Figura 6b. Transformada de Fourier de la señal temporal anterior. Página 5 de 7 (7) siendo V el módulo de la velocidad de giro, y t el tiempo de registro. El término cos(ωot) aparece4) como consecuencia de que a pesar de que se emite un tono puro, la cámara responde con una banda estrecha de frecuencias a su alrededor, debida a la modulación de amplitud que introduce la respuesta de la propia cámara. Si el campo fuera perfectamente difuso, el espectro de la señal sería rectangular. Las desviaciones de la forma rectangular que aparecen en medidas experimentales, son prueba de que la difusión no es del todo perfecta. La figura 6a) representa la señal temporal obtenida en la experimentación al excitar la cámara con un tono puro de 500 Hz. En ella se aprecia la variación de la presión sonora instantánea con la posición del micrófono a lo largo de la trayectoria semicircular considerada, cuyo radio fue de 1,2 metros y el tiempo empleado por el micrófono en recorrerla 8 segundos. En la figura 6b) aparece el correspondiente espectro en frecuencia de la señal temporal captada por el micrófono. Se aprecia como el módulo de la transformada de Fourier no es solamente el tono puro que se empleó para excitar la fuente sonora, sino que se incluye una banda de frecuencias muy estrecha 2Vf 0 c , centrada en la señal de excitación, f0 (500 Hz), y que corresponde a la respuesta del recinto. En la figura 7a) se muestra la función de autocorrelación de la señal temporal representada en 6a, mostrando una gran similitud con la ecuación 2 que corresponde a uno de los criterios fundamentales admitido actualmente para confirmar la buena difusión del campo acústico en un recinto. Las pequeñas discrepancias son perfectamente achacables a los errores experimentales y de cálculo. La figura 7b) representa el módulo de la transformada de Fourier de la función de autocorrelación de la señal temporal, mostrando una gran analogía con el espectro obtenido directamente de la señal temporal, lo cual permite confirmar la validez del procedimiento seguido. Autocorrelación C [t ] = 7a sin(k 0Vt ) ⋅ cos(ω 0 t ) (k 0Vt ) 7b Figura 7a. Autocorrelación de la señal temporal (-) y la función teórica sinc(koVt)cos(ωot) (-). Figura 7b. Densidad espectral de potencia. Adicionalmente se ha repetido la experiencia para otras frecuencias encontrándose resultados análogos, empeorando la condición de buena difusión del campo acústico a medida que disminuye la frecuencia de excitación. Como comprobación complementaria se han hecho mediciones precisas de niveles sonoros en diferentes posiciones de la misma cámara, tanto con micrófonos móviles como fijos, excitando en esta ocasión la fuente con ruido aleatorio de banda ancha, encontrándose una desviación de los niveles obtenidos de ±1.5 dB en el peor de los casos, siempre en bajas frecuencias. En consecuencia, la cámara analizada puede considerarse como una buena aproximación a las condiciones ideales de campo acústico difuso en todo el rango de frecuencias de interés en acústica de la edificación, fin a que está destinada principalmente. Para otros fines con exigencias de mayor grado de difusión, el límite se sitúa a frecuencia superior, pudiendo en todo caso afirmar que a partir de la frecuencia de 450 Hz (frecuencia de Schroeder), la cámara satisface las mayores exigencias de difusión BIBLIOGRAFÍA 1. Diffusivity characteristics of the acoustic field in the reverberant room at the C.I.F. “L. Torres Quevedo”. A. Pérez-López. 5e Congress International d’Acoustique. Liège 1965. 2. Needed: a new definition of diffusion. R.H.Lyon. J.Acoust. Soc. Am., Vol 56, No 4, p. 13001302, October 1974. 3. Zur Messung der Diffusität von Schallfeldern durch Korrelation. P. Dämmig. 1957 Acustica 7, 387-398. Página 6 de 7 4. Traversing microphone spectroscopy as a means for assessing diffusion. David Lubman. J. Acoust. Soc. Am., Vol. 56, No. 4, p. 1302-1304, October 1974. AGRADECIMIENTOS El presente trabajo ha contado con la financiación del Plan Nacional de I+D nº AMB 981029-C04-01 y con la del contrato de investigación “Respuesta dinámica vibratoria de estructuras aerospaciales sometidas a excitaciones acústicas de alta intensidad, por vía aérea” entre CASA y el Instituto de Acústica. Página 7 de 7