Modelos en pequeña señal de los dispositivos electrónicos básicos

TEMA 2: MODELOS EN PEQUEÑA SEÑAL DE LOS
DISPOSITIVOS ELECTRÓNICOS BÁSICOS
d
Francisco J. Franco Peláez, Germán González Díaz e Ignacio Mártil de la Plaza
d
ri
Apuntes para uso en la asignatura Electrónica Analógica, impartida en la Ingeniería Superior
p
.u
c
m
m
o
w
:/
/
w
w
id
e
rs
tt
p
h
U
n
iv
Pa
ra
u
so
de
C
alu
m
a
d
n
os
de
la
lu
.e
te
s
n
se
d
e
M
a
Electrónica en la Facultad de Físicas de la Universidad Complutense de Madrid.
1
Modelos en pequeña señal
Tema 2
Índice
1. Modelos en pequeña señal
3
2. El diodo
4
2.1.
Modelo esencial en pequeña señal . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.2.
Extensión del modelo en pequeña señal del diodo . . . . . . . . . . . . . . . . . . .
5
3. El transistor BJT
7
Consideraciones generales sobre el modelo en pequeña señal de los transistores
3.2.
Popularidad de los modelos h
3.3.
Rotaciones entre modelos
12
3.3.2.
Rotaciones entre modelos similares con distinto nodo en común . . . . . . .
13
o de Giacoletto
15
Modelo en pequeña señal del transistor bipolar a partir del modelo SPICE . . . . . .
17
3.5.1.
Modelo de conductancias en emisor común . . . . . . . . . . . . . . . . . .
17
3.5.2.
Modelo híbrido en emisor común
. . . . . . . . . . . . . . . . . . . . . . .
18
3.5.3.
Modelos híbridos en base y colector común . . . . . . . . . . . . . . . . . .
18
3.5.4.
Modelos de Giacoletto . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
Extensión del modelo en pequeña señal . . . . . . . . . . . . . . . . . . . . . . . .
20
p
os
de
la
lu
.e
te
s
n
se
d
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e
Π
M
a
12
. . . . . . . . . . . . . . . . . . . . . . .
20
3.6.2.
Capacidades parásitas
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
o
m
Inclusión de resistencias parásitas
alu
m
a
d
n
3.6.1.
. . . . . . . . . . . . . . . . . . .
22
24
.u
c
m
de
C
Frecuencia de transición de un transistor bipolar
Parásitos en un transistor MOS. Capacidades parásitas.
. . . . . . . . . . . . . . .
27
Frecuencia de transición . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
/
w
w
id
e
rs
iv
tt
p
:/
30
h
U
n
5. El transistor JFET
w
25
so
Modelo básico a bajas frecuencias . . . . . . . . . . . . . . . . . . . . . . . . . . .
Pa
ra
u
4.3.
d
ri
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4. El transistor MOSFET
4.2.
10
. . . . . . . . . . . . . .
3.5.
4.1.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Rotaciones entre modelos con mismo nodo común
Modelo en
3.7.
7
3.3.1.
3.4.
3.6.
. . .
d
3.1.
Electrónica Analógica
Ingeniería Superior en Electrónica
2
Modelos en pequeña señal
Tema 2
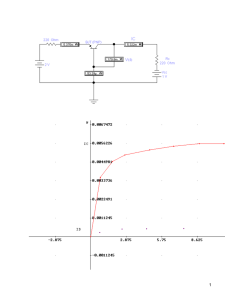
Figura 1: Ejemplo de diodo como dispositivo no lineal. Una fuente de corriente constante,
punto de operación. Las pequeñas variaciones de la corriente,
respecto del punto de operación.
d
ri
Modelos en pequeña señal
M
a
1.
VOU T ,
IQ , ja el
provocarán un cambio (no lineal)
d
en la tensión del diodo,
∆i,
En electrónica analógica, tiene interés tanto el punto de operación del circuito como el comportamiento de dicho punto de operación ante las perturbaciones. Estas perturbaciones, variables en
d
e
el tiempo, se incorporan a los circuitos en un nodo determinado y se transmiten a otros puntos de
manera inmediata. Este es el fundamento de la amplicación pues, en el fondo, la amplicación no
lu
.e
te
s
n
se
es sino la respuesta magnicada en un nodo privilegidado de un circuito, llamado salida, ante una
la
perturbación en otro, llamado entrada.
de
Existen dos modos de estudiar el efecto de las perturbaciones en la salida de un circuito. En
primer lugar, podría obtenerse la relación que existe entre el nudo de salida y el de entrada, que es
p
m
alu
m
a
d
n
os
donde hemos introducido la perturbación. En general, esta función puede ser no lineal por lo que
se debe recurrir a una simplicación a través del uso de diferenciales. Realizando un desarrollo de
C
c
m
o
Taylor en torno al punto de operación:
.u
w
no es sino
w
w
VOU T (VIN,Q )
e
rs
Pa
ra
u
Recordemos que
id
so
de
∂ 2 VOU T ∂VOU T ·∆VIN + 2
· (∆VIN )2 + . . .
VOU T (VIN,Q + ∆VIN ) = VOU T (VIN,Q ) +
∂VIN Q
∂ VIN Q
VOU T,Q ,
(1)
o tensión de salida en el punto de operación.
Pongamos un ejemplo extremadamente sencillo. Sea el circuito de Fig. 1. Suponiendo el diodo
/
:/
U
n
iv
prácticamente ideal, es fácil ver que:
VOU T
∼
− 1 = IS · exp
N ·VT
h
tt
p
IQ + ∆i = IS · exp
VOU T
N ·VT
Por lo que:
VOU T = N ·VT · ln
IQ + ∆i
IS
(2)
Operemos con esta ecuación para hacerla más apropiada:
VOU T = N ·VT · ln
Electrónica Analógica
IQ + ∆i
IS
= N ·VT · ln
IQ
IS
∆i
+ N ·VT · ln 1 +
IQ
Ingeniería Superior en Electrónica
(3)
3
Modelos en pequeña señal
Tema 2
El primer término no es sino el valor de la tensión de salida en el punto de operación, si no hubiera
ninguna perturbación o pequeña señal. ¾Qué ocurre con el segundo término? Recordemos que, de
acuerdo con la teoría de diferenciales,
ln (1 + x) =
∞
X
(−1)k+1
k=1
x2 x3
xk
=x−
+
− ...
k
2
3
así que la expresión anterior se transformaría en:
∆i
IQ
2
N ·VT
·
+
3
∆i
IQ
3
− ...
N ·VT
N ·VT
N ·VT
·∆i −
· (∆i)2 +
· (∆i)3 − . . .
2
IQ
2·IQ
3·IQ3
(4)
M
a
VOU T = VOU T,Q +
N ·VT
−
·
2
d
ri
VOU T = VOU T,Q + N ·VT ·
∆i
IQ
d
Esta ecuación es muy ilustrativa. El término constante, como se dijo antes, es la tensión en el punto
d
e
de operación. A continuación, aparece un término lineal con la perturbación. Como veremos más
adelante, este término, que es la primera derivada en el punto de operación, equivale al modelo en
lu
.e
te
s
n
se
pequeña señal del diodo. Finalmente, aparecen términos adicionales en potencias superiores.
la
En electrónica suele bastar con el cálculo de los dos primeros términos. Salvo en circunstancias
de
especiales, como al calcular la distorsión en la salida, nos basta la parte constante y la lineal de la
os
salida del circuito. La primera puede calcularse con las técnicas mostradas en el Tema 1. La segunda
p
m
alu
m
a
d
n
componente de la salida puede calcularse de dos modos: En primer lugar, resolver las ecuaciones
o
no lineales y calcular la derivada o, segundo, linealizar los componentes y resolver el circuito. Ésta
c
m
C
es la técnica que vamos a utilizar, llamada modelado en pequeña señal. Consiste en reemplazar
de
cada componente por un equivalente lineal que modele la respuesta a pequeñas perturbaciones tras
1
.u
eliminar todas las fuentes constantes del circuito
y resolver el circuito. La señal nal, sea cual sea el
w
id
so
nudo o rama estudiada, será la suma de la componente DC del punto de operación y la perturbación,
w
w
tt
p
U
Modelo esencial en pequeña señal
h
2.1.
:/
El diodo
n
2.
/
e
rs
iv
Pa
ra
u
proporcional a la señal variable de entrada.
Un diodo es un típico ejemplo de dispositivo no lineal con solo dos entradas o puertos. En este
dispositivo, la corriente que lo atraviesa,
ID ,
es función de la tensión entre ambos puertos,
VD .
Suponiendo el diodo ideal, puede usarse la ecuación de Shockley:
ID = IS · exp
VD
N ·VT
−1
(5)
1 Recuérdese que, en electronica, eliminar una fuente es darle valor nulo. Las fuentes de tensión son cortocircuitos
y las de corriente, abiertos.
Electrónica Analógica
Ingeniería Superior en Electrónica
4
Modelos en pequeña señal
Tema 2
Figura 2: Equivalente de un diodo en pequeña señal.
Normalmente, el diodo se suele estudiar en zona directa por lo que la expresión anterior se reduce a:
(6)
Calculemos ahora el equivalente en pequeña señal. Denominaremos
iD = ∆ID
M
a
que:
d
ri
d
ID = IS · exp
VD
N ·VT
y
con lo
(7)
e
∂ID 1
ID
VD
iD =
·
·vD =
·vD
·vD = IS · exp
∂VD Q
N ·VT
N ·VT
N ·VT
vD = ∆VD
d
Es decir, hay una relación lineal entre la corriente y la tensión. Esto no es sino la ecuación que
N ·VT
.
ID
lu
.e
te
s
n
se
gobernaría una resistencia de valor
la
rD =
(8)
de
Por tanto, en primera aproximación, un diodo puede aproximarse en pequeña señal como una re-
m
o
c
m
Extensión del modelo en pequeña señal del diodo
C
2.2.
alu
m
a
d
n
rD = 0.
p
os
sistencia cuyo valor se calculará con Eq. 8 (Fig. 2). En inversa, podemos suponer directamente que
.u
de
Ocurre que el modelo descrito en el apartado anterior podría tomarse como punto de partida
e
rs
podrían incorporarse los
w
Pa
ra
u
siguientes elementos:
rD
w
w
id
so
al que añadir nuevos fenómenos si fuera necesario. Así, a la resistencia
iv
Resistencia de fuga por generación-recombinación: Si polarizamos un diodo en inversa,
/
:/
n
gran parte de la corriente de fuga se produce por fenómenos de generación-recombinación y no
tt
p
U
por difusión. Puede demostrarse que estas corrientes son proporcionales al valor de la anchura
de la zona de vaciamiento,
W.
Asimismo, este parámetro crece con el valor absoluto de la
h
tensión de polarización inversa. Por tanto, debe producirse un incremento de la corriente de
fuga al aumentar la tensión inversa de polarización. Esto se modela como una resistencia de
nombre
rL ,
muy elevada, situada en paralelo con
rD .
Capacidades de unión y difusión: En toda unión PN aparecen dos capacidades parásitas:
Una, de gran importancia en directa, es la capacidad de difusión cuyo valor es proporcional a
la corriente que atraviesa el diodo:
CD =
Electrónica Analógica
ID
·τT = rD ·τT
N ·VT
Ingeniería Superior en Electrónica
5
Modelos en pequeña señal
Tema 2
Figura 3: Equivalente completo de un diodo en pequeña señal, incluyendo todos los parámetros del
d
ri
τT
el tiempo medio de tránsito, que es la media entre los tiempos de vida media de
M
a
siendo
d
Apartado 2.2.
los portadores minoritarios en cada una de las dos zonas. Evidentemente, esta capacidad está
y es despreciable en polarización inversa. Por otra parte, en todo diodo
e
rD
en paralelo con
d
aparece una capacidad de unión de valor
1+
VD
VBI
m
es la capacidad de unión con tensión nula,
VBI
el potencial de contacto de la unión
p
m un parámetro dependiente del tipo de unión, cuyo valor estará entre 1/3 y 1/2. A diferencia
os
y
CJ0
CJ0
lu
.e
te
s
n
se
donde
de
la
CJ = c
m
m
C
los parámetros anteriores.
o
alu
m
a
d
n
de la anterior, esta capacidad solo tiene importancia en inversa y está en paralelo con todos
.u
de
Resistencia serie: Dentro de un diodo, se producen caídas de tensión entre los contactos
y la zona de unión. Este hecho se modela fácilmente añadiendo una resistencia parásita,
rS .
w
id
Pa
ra
u
so
Esta resistencia tiene gran importancia tanto en DC como en pequeña señal y está en serie
w
w
e
rs
con el paralelo formado por todos los dispositivos anteriores.
/
iv
En consecuencia, todo diodo puede modelarse en pequeña señal tal y como se muestra en Fig. 3.
:/
C D , rD
y
CJ
ni
rS .
h
tt
p
y en inversa, donde puede prescindirse de
U
rL ,
n
Este modelo puede simplicarse si el diodo está en directa, pues no tendrían importancia ni
Electrónica Analógica
Ingeniería Superior en Electrónica
6
Modelos en pequeña señal
Tema 2
(a)
(b)
Figura 4: Tensiones y corrientes en un transistor BJT, NPN (a) o PNP (b).
d
ri
3.1.
d
El transistor BJT
Consideraciones generales sobre el modelo en pequeña señal de
M
a
3.
los transistores
d
e
A diferencia de los diodos, los transistores, sean bipolares o de efecto campo, son dispositivos en
2
los que intervienen varias corrientes y tensiones. En el caso de los transistores bipolares , debemos
lu
.e
te
s
n
se
hablar de las corrientes y tensiones de colector, base y emisor. En total, el estado de un transistor
la
se debe describir con seis parámetros eléctricos (IC ,
IB , IE , VC , VB
y
VE ). Sin embargo, la realidad
de
es algo más sencilla. En primer lugar, existe una relación de ligadura en las corrientes debido a que
un transistor se comporta en los circuitos como un nudo y, por tanto, la suma de las corrientes
p
m
C
o
en Fig. 4, se debe cumplir que:
IE = IB + IC
(9)
c
m
alu
m
a
d
n
os
entrantes es igual a la suma de las salientes. Así, si aceptamos el criterio de las corrientes mostrado
.u
de
independientemente del tipo de transistor. Por otra parte, en un transistor no nos interesan las
w
so
tensiones absolutas en sus nudos sino la diferencia que existe entre ellos. Por ello, podemos elegir
w
w
id
Pa
ra
u
un único nudo como nudo de referencia y expresar las tensiones de los otros dos utilizando a este
e
rs
de referencia. La elección realizada afecta a las ecuaciones que gobiernan el transistor y, por tanto,
/
iv
al modelo en pequeña señal. Por ello, existen tres grandes familias de modelos en pequeña señal:
:/
n
Colector común, base común y emisor común, dependiendo de la elección del colector, base o
tt
p
U
emisor como nudo de referencia. En cualquier caso, el número de tensiones implicadas se reduce a
2 al utilizarse un nudo como referencia.
h
En resumen, todo transistor posee cuatro parámetros eléctricos esenciales (dos corrientes y dos
tensiones) que modelan el comportamiento en DC y, como es presumible, en pequeña señal. Las
corrientes pueden expresarse en función de las tensiones entre los nodos de un transistor de esta
2 El desarrollo teórico que viene a continuación podría aplicarse sin problema a los transistores de efectos campo.
Sin embargo, como veremos más adelante, no es tan interesante al contar éstos con un terminal por el que no puede
circular corriente (puerta), que hace que un transistor de efecto campo se encuentre algo más cercano a un elemento
de dos terminales como el diodo..
Electrónica Analógica
Ingeniería Superior en Electrónica
7
Modelos en pequeña señal
Tema 2
Figura 5: Representación de un transistor como una bipuerta. El nudo común se ha dividido en dos
para facilitar la comprensión de las tensiones
modo:
vk .
y
g,
d
ri
f
que ya se esbozaron en el Tema 1.
M
a
Más adelante recordaremos cuales son estas funciones
d

 I = f (V , V )
C
BE
BC
 I = g (V , V )
E
BE
BC
Desde el punto de vista puramente matemático, podríamos operar con la expresión anterior para
fX
y
gX
tales que:
d
podríamos buscar dos nuevas funciones
e
reexpresar las dos ecuaciones cambiando los parámetros independientes y dependientes. Por ejemplo,
de
la
lu
.e
te
s
n
se

 I = f (V , I )
C
X
BE E
 V = g (V , I )
BC
X
BE E
p
os
que serían también perfectamente lícitas. ¾Adónde llegamos entonces? Simplemente a que hay cuatro
m
alu
m
a
d
n
parámetros eléctricos que denen el estado de un transistor y en los que dos pueden funcionar
e
Y2
del conjunto
X1
y
X2 .
expresarlo en función de los dos parámetros
.u
Es decir:

 Y = f (X , X )
1
1
1
2
 Y = f (X , X )
2
2
1
2
w
w
w
id
e
rs
Pa
ra
u
so
de
restantes, simbolizados como
{I1 , I2 , V1 , V2 }y
c
m
Y1
C
dos parámetros
o
como variables independientes y otros dos como dependientes. En otras palabras, se pueden escoger
(10)
/
:/
iv
¾Cuantas posibilidades hay? Haciendo un estudio rápido de combinaciones, se deduce que hay 6
U
n
posibilidades distintas, que desarrollaremos más adelante. La primera conclusión de esta idea es
tt
p
que al haber dos tensiones y dos corrientes, todo transistor debería poder modelarse como una
h
bipuerta similar a Fig. 5, habiendo dos parámetros independientes y dos dependientes. Hay que
indicar, además, que los parámetros simbolizados con el subíndice 1 se conocen como de entrada
y aquellos con el subíndice 2 como de salida. Continuando con el desarrllo, el modelo en pequeña
señal debe ser la linealización de Eq. 10. Por tanto:

 y =
1
 y =
2
Electrónica Analógica
∂f1
·x
∂X1 1
+
∂f1
·x
∂X2 2
∂f2
·x
∂X1 1
+
∂f2
·x
∂X2 2
Ingeniería Superior en Electrónica
(11)
8
Modelos en pequeña señal
Tema 2
Nombre
Símbolo
Independientes
Dependientes
Salida
a
v2 , i2
v1 , i1
Entrada
b
v1 , i1
v2 , i2
m
v1 , i2
i1 , v2
Híbrido
h
i1 , v2
v1 , i2
Impedancias
z
i1 , i2
v1 , v2
Admitancias
y
v1 , v2
i1 , i2
Ecuaciones
d
ri
d
v1 = a11 ·v2 + a12 ·i2
i1 = a21 ·v2 + a22 ·i2
v2 = b11 ·v1 + b12 ·i1
i2 = b21 ·v1 + b22 ·i1
i1 = m11 ·v1 + m12 ·i2
v2 = m21 ·v1 + m22 ·i2
v1 = h11 ·i1 + h12 ·v2
i2 = h21 ·i1 + h22 ·v2
v1 = z11 ·i1 + z12 ·i2
v2 = z21 ·i1 + z22 ·i2
i1 = y11 ·v1 + y12 ·v2
i2 = y21 ·v1 + y22 ·v2
yk ≡ ∆Yk
y
xk ≡ ∆Xk .
3
Esta expresión puede reescribirse de modo matricial :
!
·
x1
x2
!
=
a11 a12
a21 a22
lu
.e
te
s
n
se
aij =
=
∂f1
∂X2
∂f2
∂X2
∂f1
∂X1
∂f2
∂X1
!
·
x1
x2
!
(12)
∂fi 4
. Ahora es cuando tenemos que precisar qué variables serán independientes y
∂Xj
de
donde
!
la
y1
y2
d
e
donde
M
a
Cuadro 1: Distintos modelos para un transistor de acuerdo con el modelo de bipuerta.
cuales dependientes pues eso nos denirá la familia de parámetros. Las combinaciones posibles se
p
m
alu
m
a
d
n
os
muestran en el Cuadro 1. Se deben hacer varias puntualizaciones a esta tabla.
o
1. Como se verá posteriormente, el modelo de bipuerta es independiente del tipo de transistor.
c
m
de
C
En particular, da igual si el transistor BJT es NPN o PNP.
.u
2. Cada conguración de transistor (emisor, base o colector común) dispone del conjunto de
w
w
e
rs
Pa
ra
u
transistor en pequeña señal.
w
id
so
seis modelos de bipuerta mostrado en el Cuadro 1. Por tanto, hay 18 modelos posibles de un
/
iv
3. Los 18 modelos describirían al mismo transistor. Consecuentemente, cualquier sistema de
:/
n
ecuaciones de la última columna del Cuadro 1 puede transformarse en cualquier otra del
tt
p
U
cuadro, incluso suponiendo que la segunda esté en otra conguración de nudo común. Así,
los parámetros z de la conguración de emisor común podrían obtenerse de cualquiera de
h
los otros modelos. Por ejemplo, a partir del conjunto de parámetros h en base común. Estos
procedimientos matemáticos se conocen, en general, como rotaciones.
En la práctica, la inmensa mayoría de las veces los problemas de respuesta en pequeña señal de
transistores bipolares se resuelven utilizando los parámetros h en base, colector o emisor común.
El resto de familias de parámetros carece de interés práctico salvo, en ocasiones, el conjunto de
3 Desde el punto de vista matemático, la matriz no es sino la matriz diferencial o jacobiano de una función de
en
R
m
Rn
.
4 Debe tenerse en cuenta que estas derivadas parciales se realizan en torno al punto de operación del transistor
Electrónica Analógica
Ingeniería Superior en Electrónica
9
Modelos en pequeña señal
Tema 2
Nombre
Entrada
Salida
Emisor
Colector
Base
Emisor
Emisor común
Base
Colector
d
ri
Base común
Colector común
d
Figura 6: Equivalencia circuital del modelo de admitancias, y, de un transistor bipolar.
Cuadro 2: Terminales de entrada y salida convencionales asociados a los distintos modelos h de un
M
a
transistor bipolar.
d
h
Popularidad de los modelos
la
3.2.
lu
.e
te
s
n
se
describirán con más detalle en el siguiente apartado.
e
parámetros y. Este modelo es equivalente al subcircuito mostrado en Fig. 6. Los modelo h se
de
Es tanto el uso que se da a los modelos h que se ha convenido qué terminal funciona como
hij ,
acordes con su
p
os
entrada y cuál de salida y se le ha dado un nombre especíco a los parámetros
m
alu
m
a
d
n
sentido físico, datos que se suministran en el Cuadro 2. Recordemos que la entrada corresponde a la
o
parte izquierda de Fig. 5, marcada con subíndice 1 y la salida a la parte derecha, cuyos términos están
c
m
C
marcados con un subíndice 2. Por otra parte, no se suelen numerar los parámetros h como elementos
h11
w
suele estar relacionado con la impedancia de entrada del transistor bipolar en
so
Así, el parámetro
.u
de
de una matriz sino con letras, como se muestra en el Cuadro 3. Estas letras tienen signicado físico.
hiX 5 .
w
w
id
Pa
ra
u
pequeña señal por lo que se lo suele denominar
e
rs
Por ello, las ecuaciones del cuadro 1 se convierten las siguientes:
/
:/
tt
p
U
n
iv
Base común:
veb = hib ·ie + hrb ·vcb
ic = hf b ·ie + hob ·vcb
(13)
vbc = hic ·ib + hrc ·vec
ie = hf c ·ib + hoc ·vec
(14)
vbe = hie ·ib + hre ·vce
ic = hf e ·ib + hoe ·vce
(15)
h
Colector común:
Emisor común:
5 La letra i proviene de input.
Electrónica Analógica
Ingeniería Superior en Electrónica
10
Modelos en pequeña señal
Tema 2
Nombre
Base Común
Colector Común
Emisor Común
h11
h12
h21
h22
hib
hrb
hf b
hob
hic
hrc
hf c
hoc
hie
hre
hf e
hoe
M
a
d
ri
d
Cuadro 3: Notación alternativa y más popular de los parámetros de los modelos bipuerta en h.
(b)
C
o
(c)
p
(d)
c
m
m
alu
m
a
d
n
os
de
la
lu
.e
te
s
n
se
d
e
(a)
de
Figura 7: Equivalente circuital de los modelos híbridos. (a) General, (b) base común, (c) colector
.u
w
id
so
común y (d) emisor común.
w
w
e
rs
Pa
ra
u
Teniendo en cuenta que las ecuaciones del modelo híbrido general se pueden asociar al circuito
mostrado en Fig. 7a, cada una de las tres ecuaciones anteriores se puede asociar a las guras
/
:/
iv
restantes. Y aquí llegamos al objetivo de estos dos primeros apartados. A la hora de hacer el modelo
tt
p
U
n
en pequeña señal de un circuito con transistores BJT, estos deben reemplazarse por cualquiera
de esta tres subredes. Evidentemente, es necesario relacionar el valor de cada parámetro con las
h
corrientes y tensiones en el punto de operación. Sin embargo, previamente es necesario saber como
se relacionan los distintos modelos entre sí. A n de cuentas, aunque haya 18 maneras distintas
de representar un transistor en pequeña señal, todas ellas representan al mismo transistor por lo
que deben poder relacionarse entre sí. Las relaciones matemáticas que permiten obtener un modelo
a partir de otro se denominan rotaciones por similitud con otros problemas matemáticos y se
estudiarán en el siguiente apartado.
Electrónica Analógica
Ingeniería Superior en Electrónica
11
Modelos en pequeña señal
Tema 2
3.3.
Rotaciones entre modelos
Hay dos tipos de rotaciones. Puesto que todo modelo en pequeña señal tiene dos pares de
magnitudes de entrada/salida (Cuadro 1) que dependen del terminal que se haya denido como
común (Cuadro 2), las rotaciones serán:
1. Fijando el nodo común, rotaciones entre modelos.
2. Fijando el modelo, rotaciones entre ese modelo con distintos nudos comunes.
En algunos casos, es necesario realizar dos pasos. Por ejemplo, para pasar del modelo h en emisor
d
ri
d
común al modelo z en base común, habría que ir desde el primero al modelo h en base común y
desde éste al modelo z en base común. O bien, pasar del primero al modelo z en emisor común y de
M
a
éste al modelo z en base común. Fijémonos que este comportamiento es similar a las rotaciones
físicas ya que primero nos movemos en una dirección y después en otra. Claro que, a diferencia
e
de las rotaciones físicas, hay conmutatividad en los movimientos. Sea cual sea el camino seguido,
lu
.e
te
s
n
se
Rotaciones entre modelos con mismo nodo común
la
3.3.1.
d
llegamos al mismo destino.
de
Algunas de las rotaciones entre modelos son inmediatas pues basta con invertir la matriz de turno
os
para obtener la matriz con nuevas variables de entrada. Así, por ejemplo, la matriz de impedancias,
p
m
·
⇒
y11 y12
y21 y22
!−1
/
w
w
=
.u
!
w
id
z11 z12
z21 z22
!
c
m
v1
v2
C
=
!
o
y11 y12
y21 y22
e
rs
iv
Pa
ra
u
so
por lo que:
!
de
i1
i2
alu
m
a
d
n
z, puede obtenerse facilmente si se conoce la matriz de admitancias, y, ya que:
v1
v2
!
=
y11 y12
y21 y22
!−1
i1
i2
·
yji
⇒ zij = (−1)i+j · y11 y12
y21 y22
!
:/
U
n
Esta relación es perfectamente reversible. Relaciones similares existen entre los parámetros a y b y
tt
p
entre m y h. Desafortunadamente, en otros casos la relación no es tan sencilla. Centrémonos en el
h
cálculo del paso del modelo y al modelo h ya que este cambio será utilizado con posterioridad. En
caso de buscar otras relaciones, puede seguirse el mismo método o consultar la bibliografía sobre el
tema.
i2 y, en la derecha, v1 y v2 . En
derecha, i1 y v2 . Nuestro objetivo será
De acuerdo con el modelo y, en la parte izquierda aparecen
cambio, en el modelo h, en la izquierda están
v1
e i2 y, en la
i1
e
reorganizar las ecuaciones del modelo y de tal modo que se asemejen a las del h:
i1 = y11 ·v1 + y12 ·v2
i2 = y21 ·v1 + y22 ·v2
Electrónica Analógica
Ingeniería Superior en Electrónica
12
Modelos en pequeña señal
Tema 2
En primer lugar, trabajemos con la ecuación superior. Despejando
v1 =
1
·i
y11 1
−
v1
se obtiene:
y12
·v
y11 2
i2 = y21 ·v1 + y22 ·v2
En la segunda ecuación, nos interesa deshacernos de
v1
en la parte de la derecha. Lo que haremos
será, simplemente, insertar la primera ecuación en la segunda:
v1 = y111 ·i1 − yy12
·v2
11
y12
y21
1
i2 = y21 · y11 ·i1 − y11 ·v2 + y22 ·v2 = y11 ·i1 + y22 −
y21 ·y12
y11
·v2
d
ri
d
y con esto habríamos completado la transformación pues el sistema inicial se ha expresado al modo
Esta tabla es fácilmente reversible, como se muestra en el Cuadro 5.
Parámetro
h11 , hi
1
y11
h12 , hr
lu
.e
te
s
n
se
la
y21
y11
h22 , ho
− yy12
11
y22 −
y21 ·y12
y11
p
os
de
h21 , hf
valor
e
valor
d
Parámetro
M
a
de los parámetros h. En consecuencia, podemos realizar la identicación recogida en el Cuadro 4.
m
y11
w
w
id
y12
− hh12
11
h21
h11
y22
h22 −
h21 ·h12
h11
/
e
rs
1
h11
w
de
so
:/
Cuadro 5: Obtención de parámetros y a partir de los modelos en h.
tt
p
U
n
iv
Pa
ra
u
Rotaciones entre modelos similares con distinto nodo en común
h
3.3.2.
valor
c
m
valor
C
Parámetro
y21
Parámetro
.u
o
alu
m
a
d
n
Cuadro 4: Obtención de parámetros h a partir de los modelos en y.
Por comodidad, vamos a centrarnos solo en las transformaciones que se pueden realizar entre
modelos h de base, colector o emisor común. El procedimiento sería parecido al descrito en el
apartado anterior pero debe tenerse en cuenta una complicación adicional: Las tensiones y corrientes
envueltas en un modelo no aparecen en el otro. Así, por ejemplo, podemos ver que en el modelo h
en base común intervienen como corrientes ie e ic en tanto que en el modelo en emisor común ie es
reemplazada por
ib .
Por tanto, no basta con trasformar el sistema de ecuaciones sino que hay que
Electrónica Analógica
Ingeniería Superior en Electrónica
13
Modelos en pequeña señal
Tema 2
reemplazar variables. Para ello, debemos recordar que Eq. 9 se transforma en pequeña señal en:
ie = ic + ib
(16)
y que todas las diferencias de tensión están relacionadas entre sí. Deduzcamos, por ejemplo, como
se pasa del modelo en emisor común al modelo en colector común:
vbe = hie ·ib + hre ·vce
ic = hf e ·ib + hoe ·vce
d
Es necesario reexpresarla como
vce = −vec .
M
a
En primer lugar, recordemos que
d
ri
vbc = hic ·ib + hrc ·vec
ie = hf c ·ib + hoc ·vec
vbe = vbc + vce = vbc − vec con lo que así
librarse de ic para lo que utilizaremos Eq. 16:
Asimismo,
d
e
podremos eliminar esta variable. Finalmente, hay que
la
lu
.e
te
s
n
se
vbc − vec = hie ·ib − hre ·vec
ie − ib = hf e ·ib − hoe ·vec
de
Reordenando el sistema de ecuaciones:
p
m
o
alu
m
a
d
n
os
vbc = hie ·ib + (1 − hre ) ·vec
ie = (1 + hf e ) ·ib − hoe ·vec
c
m
C
Sin embargo, esta ecuación aún no se puede aplicar. El motivo es sencillo: De acuerdo con Eq. 16,
.u
de
la corriente de emisor es saliente. Sin embargo, en el modelo en colector común es entrante. ¾Cómo
podemos solucionar esto? Simplemente, redenamos la corriente de emisor del sistema anterior con
/
w
vbc = hie ·ib + (1 − hre ) ·vec
ie = − (1 + hf e ) ·ib + hoe ·vec
:/
iv
n
w
w
id
De este modo, el sistema de ecuaciones se convertiría en:
e
rs
so
ie → −ie .
Pa
ra
u
el cambio
tt
p
Parámetro
Valor
Parámetro
vValor
hic
hie
hrc
1 − hre
hf c
− (1 + hf e )
hoc
hoe
h
U
Ahora sí se puede identicar el sistema con Eq. 14 como recoge el Cuadro 6.
Cuadro 6: Obtención de parámetros h en colector común a partir de los modelos en emisor común.
Análogamente se podría realizar el cálculo de los parámetros en base común a partir de los
Electrónica Analógica
Ingeniería Superior en Electrónica
14
Modelos en pequeña señal
Tema 2
Figura 8: Modelo de Giacoletto de un transistor bipolar.
parámetros en emisor común. Sin embargo, el razonamiento matemático es tedioso y no se mostrará
Valor
Parámetro
hib
hie
1+hf e
hrb
hf b
− 1+hf ef e
h
hob
vValor
− hre
d
e
hie ·hoe
1+hf e
M
a
Parámetro
d
ri
d
aquí. Los resultados serían los recogidos en el Cuadro 7.
lu
.e
te
s
n
se
hoe
1+hf e
de
la
Cuadro 7: Obtención de parámetros h en base común a partir de los modelos en emisor común.
p
os
Lógicamente, las relaciones de los cuadros 6 y 7 son reversibles, siendo más sencillas en el primer
m
alu
m
a
d
n
caso. Por otra parte, es posible la transformación directa entre base y colector común. Sin embargo,
o
como veremos más adelante, es muy fácil obtener el modelo en emisor común y relacionarlo con
c
m
C
el punto de operación del transistor. Por ello, nos hemos centrado en obtener los otros parámetros
.u
de
a partir de esta conguración y no estudiaremos las otras posibles relaciones al no tener utilidad
Π
w
w
w
Modelo en
e
rs
3.4.
id
Pa
ra
u
so
directa en la asignatura.
o de Giacoletto
/
:/
iv
A veces, no interesa que el modelo en pequeña señal del transistor tenga dos fuentes dependientes.
U
n
Para evitarlo, existe un modelo alternativo llamado en
Π
que se caracteriza por la existencia de
tt
p
una impedancia que une la entrada con la salida. Esta estructura sería similar a la mostrada en Fig.
gµ
y
go )
y una transconductancia,
gm .
Es fácil establecer
h
8, donde existen tres conductancias (gπ ,
una relación entre estos parámetros y los modelos en admitancia e híbridos. Así, la relación que
existe entre este subcircuito y el modelo en admitancias se recoge en el Cuadro 8 en tanto que el
Cuadro 9 recoge las equivalencias con el modelo híbrido.
La obtención de estas equivalencias es relativamente sencilla. Pongamos por ejemplo la obtención
de los parámetros de Giacoletto en función de los parámetros del modelo de inductancias. Para ello,
examinemos el circuito de Fig. 8. En él, se puede demostrar que el valor de las corrientes i1 e i2 es,
Electrónica Analógica
Ingeniería Superior en Electrónica
15
Valor
Parámetro
Valor
y11
gπ + gµ
gπ
y11 + y12
y12
−gµ
gµ
−y12
y21
gm − gµ
gm
y21 − y12
y22
go + gµ
go
y22 + y12
d
ri
Parámetro
d
Modelos en pequeña señal
Tema 2
hi
1
gπ +gµ
gπ
hr
gµ
gπ +gµ
la
m
p
de
os
gm −gµ
gπ +gµ
alu
m
a
d
n
C
1−hr
hi
gµ
hr
hi
gm
hr +hf
hi
go
ho − hr ·h−1
i · (1 + hf )
.u
de
c
m
m
go + gµ · ggππ+g
+gµ
ho
o
hf
Valor
e
Parámetro
d
Valor
lu
.e
te
s
n
se
Parámetro
M
a
Cuadro 8: Equivalencia entre modelo de Giacoletto y de admitancias.
w
id
so
Cuadro 9: Equivalencia entre modelo de Giacoletto e híbrido en h.
w
w
:/
/
e
rs
i1 = gπ ·v1 + gµ · (v1 − v2 )
i2 = go ·v2 + gµ · (v2 − v1 ) + gm ·v1
tt
p
U
n
iv
Pa
ra
u
de acuerdo con la ley de las corrientes de Kircho:
h
Si reordenamos las ecuaciones, el anterior sistema de ecuaciones se convierte en:
i1 = (gπ + gµ ) ·v1 − gµ ·v2
i2 = (gm − gµ ) ·v1 + (go + gµ ) ·v2
Pero esto no es sino la expresión matemática del modelo en admitancias que conduce a las equivalencias de las dos primeras columnas del Cuadro 8. El resto de equivalencias, recogidas en este
cuadro y en el Cuadro 9, se pueden demostrar de manera trivial.
Este modelo es muy popular en los textos relacionados con la electrónica por un hecho impor-
Electrónica Analógica
Ingeniería Superior en Electrónica
16
Modelos en pequeña señal
Tema 2
tante: Es equivalente al modelo en pequeña señal de los transistores JFET y MOSFET sin efecto
gπ , gµ → 0.
sustrato haciendo, simplemente,
De este modo, los equivalentes en pequeña señal de
las distintas conguraciones pueden obtenerse para el caso bipolar y obteniendo el caso FET como
caso particular.
3.5.
Modelo en pequeña señal del transistor bipolar a partir del modelo SPICE
Modelo de conductancias en emisor común
d
3.5.1.
d
ri
Sabemos que, en DC, las ecuaciones que gobiernan un transistor bipolar NPN son:
VBE
NF VT
IC = IS · exp
1
VBC
− 1 − IS · 1 +
exp
−1
βR
NR VT
e
d
M
a
1
VBE
VBC
IE = IS · 1 +
· exp
− 1 − IS · exp
−1
βF
NF VT
NR VT
lu
.e
te
s
n
se
En general, los transistores bipolares tienen interés en diseño analógico cuando están en zona activa
la
directa. En estas circunstancias, la ecuación anterior se transforma en:
p
m
VBE
NF VT
(17)
VBE
NF VT
(18)
c
m
o
· exp
IC = IS · exp
C
alu
m
a
d
n
os
de
1
IE = IS · 1 +
βF
de
Si deseamos pasar estas ecuaciones a pequeña señal según Eq. 11, podemos ver que obtendríamos
.u
un modelo de admitancias. Asimismo, nos encontramos con dos opciones: Buscar el modelo en base
w
id
so
común o el modelo en emisor común. A favor del primero, está que las corrientes DC son las de
w
w
e
rs
Pa
ra
u
este modelo (ie , ic ). Sin embargo, si escogemos la segunda opción, veríamos que podemos añadir
sin problemas el efecto Early, que depende de
/
IE
Por ello, nos inclinaremos por esta solución.
con la tranformación
IB = IE − IC . Asimismo, multiplicaremos
:/
iv
En primer lugar, eliminaremos
VCE .
tt
p
h
U
n
la corriente de colector por el factor Early:
IS
IB =
· exp
βF
IC = IS · exp
VBE
NF VT
VBE
NF VT
VCE
· 1+
VAF
(19)
(20)
Calculemos entonces los valores del modelo de admitancias en emisor común:
y11,e
Electrónica Analógica
∂IB
IS
=
· exp
=
∂VBE
βF
VBE
NF VT
·
1
IB
=
NF ·VT
NF ·VT
Ingeniería Superior en Electrónica
(21)
17
Modelos en pequeña señal
Tema 2
∂IB
=0
∂VCE
VBE
VCE
1
IC
∂IC
= IS · exp
· 1+
·
=
=
∂VBE
NF VT
VAF
NF ·VT
NF ·VT
∂IC
VBE
1
IC
y22,e =
= IS · exp
·
'
∂VCE
NF VT
VAF
VAF
y12,e =
y21,e
Realmente, el parámetro
(22)
(23)
(24)
y12,e no es nulo debido a efectos de segundo orden no incluidos en el modelo
SPICE. Sin embargo, a efectos prácticos, se considerará así a partir de ahora.
En caso de trabajar con un PNP, se habrían obtenido resultados idénticos. En general, no hay
d
ri
d
diferencia entre los modelos en pequeña señal de los transistores PNP y NPN salvo, claro está, la
posición del emisor. Así, en general, el emisor de los NPN está a menos tensión absoluta que el
M
a
colector en tanto que, en los PNP, ocurre lo contrario. Grácamente, en un NPN el colector suele
estar arriba y el emisor abajo, y en los PNP ocurre al revés. Este hecho debe recordarse cuando se
Modelo híbrido en emisor común
lu
.e
te
s
n
se
3.5.2.
d
e
proceda a crear el modelo en pequeña señal de un circuito con transistores.
la
Eq. 21-24 nos permiten obtener los valores de los parámetros híbridos en emisor común cuando
id
hoe
− yy12
≈0
11
y22 −
y21 ·y12
y11
≈
IC
VAF
.u
IC
IB
hre
valor
w
de
=
c
m
m
NF ·VT
IB
C
y21
y11
hf e
so
=
o
alu
m
a
d
n
1
y11
hie
Parámetro
p
valor
os
Parámetro
de
se combinan con el Cuadro 4. Estos resultados se muestran en el Cuadro 10.
w
w
Pa
ra
u
Cuadro 10: Parámetros h a partir de las corrientes en el punto de operación, temperatura y carac-
/
iv
e
rs
terísticas propias del transistor.
:/
n
Deben tenerse en cuenta algunos hechos. En primer lugar, como se dijo antes, el parámetro
hre
tt
p
U
es, en general, despreciable aunque no sea exactamente nulo. Por ese motivo, el modelo híbrido en
emisor común es equivalente al subcircuito de Fig. 9. Por otro lado, el valor de
hf e
coincide con
en los transistores ideales aunque, en la realidad, puede haber alguna variación.
3.5.3.
Modelos híbridos en base y colector común
h
hF E , βF
Los resultados del Cuadro 10 nos permiten obtener los valores de los parámetros híbridos en el
resto de conguraciones. Así, para la conguración de colector común se obtendría la representación
del Cuadro 11.
Electrónica Analógica
Ingeniería Superior en Electrónica
18
Modelos en pequeña señal
Tema 2
Figura 9: Circuito simplicado equivalente al modelo híbrido en emisor común.
valor
Parámetro
valor
hic
NF ·VT
IB
hrc
≈1
≈
hoc
d
ri
IC
VAF
e
IC
IB
M
a
− 1+
hf c
d
Parámetro
lu
.e
te
s
n
se
d
Cuadro 11: Obtención de parámetros h en colector común a partir del punto de operación.
Debe resaltarse un hecho realmente importante. En emisor común, el parámetro
hre ·vce
la
ciable por lo que l.a fuente de tensión con valor
hre
es despre-
no aparece en los cálculos derivados de modo
de
que, en la entrada del transistor (base), hay una simple resistencia al nudo común. Sin embargo,
hrc
prácticamente igual a
p
os
en este modelo jamás se debe hacer esta simplicación al ser el factor
m
alu
m
a
d
n
1. El subcircuito equivalente sigue siendo el mostrado en Fig. 7c. En el modelo en base común, los
.u
w
w
e
rs
id
so
h
hrb
valor
hie ·hoe
1+hf e
− hre ≈
hoe
1+hf e
≈
− hre ≈ 0
IB
VAF
/
hob
N ·VT
VAF
:/
iv
NF ·VT
IE
− 1+hf ef e ≈ −αF
hf b
n
≈
Parámetro
w
hie
1+hf e
hib
c
m
C
valor
de
Parámetro
Pa
ra
u
o
parámetros adquieren los valores mostrados en el Cuadro 12.
tt
p
U
Cuadro 12: Obtención de parámetros h en base común a partir del punto de operación.
h
Para realizar las aproximaciones y dejar las ecuaciones de este modelo de un modo sencillo, se ha
supuesto que
inuye en la
hf e ≡ hF E ≡ βF >> 1. A semejanza del modelo en emisor común, la salida apenas
entrada pues hrb ≈ 0. Por ello, el circuito equivalente es igual al de Fig. 7b aunque
puede eliminarse la fuente de tensión dependiente.
3.5.4.
Modelos de Giacoletto
En principio, nada excluye que se pueda denir un modelo en
Π
en emisor común, base común
o colector común. Sin embargo, en la práctica, solo tiene interés el modelo de Giacoletto en emisor
Electrónica Analógica
Ingeniería Superior en Electrónica
19
Modelos en pequeña señal
Tema 2
Valor
1−hr
hi
gπ
≈
1
hie
hr
hi
gµ
hr +hf
hi
gm
≈
≈
IB
N ·VT
≈0
hf e
hie
≈
IC
N ·VT
ho − hr ·h−1
i · (1 + hf ) ≈ ho =
IC
VAF
d
ri
go
d
Parámetro
M
a
Cuadro 13: Equivalencia entre los parámetros del modelo de Giacoletto e híbrido en h en conguración de emisor común.
lu
.e
te
s
n
se
las equivalencias son las mostradas en el Cuadro 13.
d
e
común. Como es lógico, en este modelo la entrada es la base y la salida el colector. De este modo,
Podemos ver que este modelo se ha reducido a una leve modicación del modelo híbrido en
hie
por su conductancia equivalente y en el que la fuente de corriente
la
emisor común reemplazando
de
dependiente de corriente se ha sustituido por una fuente de corriente dependiente de tensión. Sin
os
embargo, como veremos más adelante, este modelo recobra todo su interés a altas frecuencias debido
p
m
c
m
Extensión del modelo en pequeña señal
C
3.6.
o
alu
m
a
d
n
a la aparición de capacidades parásitas que conectan base y colector.
.u
de
Como es bien sabido, en todo dispositivo aparecen parásitos que pueden ser incluidos en el
w
id
w
w
3.6.1.
e
rs
Pa
ra
u
so
modelo en pequeña señal. Estos parásitos son, básicamente, resistencias y capacidades parásitas.
Inclusión de resistencias parásitas
/
:/
iv
En todo transistor bipolar existen tres resistencias parásitas, cada una de ellas referida a un
tt
p
U
n
terminal. Así, el modelo híbrido en emisor común se transformaría en el mostrado en Fig. 10. Deben
tenerse en cuenta varios puntos.
h
1. La geometría del colector y emisor permite modelar correctamente la resistencia parásita como
una resistencia simple en serie. En cambio, la resistencia de base puede dividirse en varias para
6
modelar mejor el comportamiento de ésta .
2. En el caso del modelo en
Π,
la caída de tensión que controla fuente de corriente no se debe
medir entre base y emisor sino entre los extremos de
gπ .
3. En general, la resistencia de emisor es despreciable frente a las otras.
6 Consultar el modelo SPICE completo para tener más detalles
Electrónica Analógica
Ingeniería Superior en Electrónica
20
Modelos en pequeña señal
Tema 2
de
la
lu
.e
te
s
n
se
d
e
M
a
d
ri
d
Figura 10: Inclusión de resistencias parásitas en el modelo híbrido en emisor común.
p
c
m
m
Capacidades parásitas
o
3.6.2.
alu
m
a
d
n
os
Figura 11: Inclusión de capacidades parásitas en el modelo de Giacoletto en emisor común.
C
Mayor importancia que las resistencias parásitas tienen las capacidades parásitas. Recordemos
.u
de
que en toda unión PN pueden darse dos capacidades: Difusión, en directa, y unión, en inversa. Como
Cπ
y la de unión entre base y colector, denominada
Cµ .
El por
w
w
e
rs
Pa
ra
u
en la unión BE, que se denomina
w
id
so
nos estamos centrando en el BJT en activa directa, solo nos deben interesar la capacidad de difusión
qué de estos nombres surge de manera natural una vez que se incorporan al modelo de Giacoletto
n
/
le da el nombre.
:/
iv
en emisor común (Fig. 11). Como se ve, cada capacidad está en paralelo con la conductancia que
tt
p
U
Lógicamente, ambas dependen del punto de operación. Así, el valor de
gm
h
transconductancia
multiplicada por el tiempo medio de tránsito,
Cπ = τF ·gm ≈ τF ·
IC
N ·VT
τF .
Cπ
no es sino el de la
Por tanto:
(25)
en tanto que la capacidad de unión entre base y colector es:
Cµ = CJBC,Q = CJBC,0
1+
VBC.Q
VBI
M
(26)
Por otra parte, si se toma en cuenta el sustrato debe añadirse una nueva capacidad de unión
Electrónica Analógica
Ingeniería Superior en Electrónica
21
Modelos en pequeña señal
d
Tema 2
la
lu
.e
te
s
n
se
d
e
M
a
d
ri
Figura 12: Inclusión de capacidades y resistencias parásitas en el modelo híbrido en emisor común.
de
Figura 13: Inclusión de capacidades y resistencias parásitas en el modelo híbrido en base común.
En general, el sustrato estará conectado a una fuente de tensión
p
CJC,S .
os
entre colector y sustrato,
m
alu
m
a
d
n
constante dependiendo del tipo de transistor. Esto hace que, en pequeña señal, esta capacidad esté
c
m
o
conectada entre el colector y tierra como muestra Fig. 12, donde se muestra el modelo híbrido
C
en emisor común con las tres capacidades descritas. Asimismo, se han mantenido las resistencias
.u
de
parásitas. Por otra parte, jémonos en un hecho importante. Al incorporar la capacidad de difusión,
iBX
esta fracción de
iB .
hie .
Este problema no aparece en el modelo de
w
w
e
rs
Pa
ra
u
Por ello, se ha marcado como
w
id
so
no toda la corriente de base se amplica en el colector sino solo la fracción que circula por
Giacoletto al tomar diferencias de tensión como argumento.
/
iv
La incorporación de las capacidades parásitas a los modelos híbridos en base o colector común
:/
n
es inmediata. Basta con colocar una capacidad
Cπ
entre base y emisor y otra capacidad
Cµ
entre
tt
p
U
base y colector dondequiera que estén en el dibujo del subcircuito. Así, por ejemplo, en el modelo
en base común, la incorporación de los condensadores conduce al circuito de Fig. 13. Asimismo,
h
jémonos de que no toda la corriente de emisor se amplica sino solo una fracción.
3.7.
Frecuencia de transición de un transistor bipolar
La frecuencia de transición de un transistor bipolar, y en general la de cualquier transistor, nos
permite estimar cómo de bueno es su comportamiento en frecuencia. Evidentemente, un transistor no
deja de trabajar al rebasar la frecuencia de transición sino que, simplemente, empezará a comportarse
peor a medida que nos vayamos aproximando a ella. Por otra parte, la frecuencia de transición
Electrónica Analógica
Ingeniería Superior en Electrónica
22
Modelos en pequeña señal
Tema 2
d
ri
d
(a)
M
a
(b)
Figura 14: Cálculo de la frecuencia de transición. Circuito original (a) y equivalente en pequeña señal
d
e
(b).
lu
.e
te
s
n
se
caracteriza al transistor, no al circuito donde se encuentre. Así, existen conguraciones con peor
la
comportamiento en frecuencia que la estimada directamente a través de la frecuencia de transición.
de
Finalmente, hay que indicar que esta frecuencia está relacionada solamente con el comportamiento en pequeña señal. Se pueden denir otras frecuencias relacionadas, por ejemplo, con la velocidad
p
os
de conmutación de los transistores en un paso de corte a saturación o viceversa. Sin embargo, esta
m
alu
m
a
d
n
frecuencia está fuera del objetivo de esta asignatura y no se estudiarán aquí.
c
m
C
o
La frecuencia de transición se calcula del siguiente modo. Imaginemos un transistor bipolar NPN
(el caso PNP es inmediato) con emisor a tierra, colector a una fuente de alimentación sucientemente
.u
de
alta y cuya base está polarizada por una fuente de corriente entrante,
IB ,
a la que se añade en
iIN (s) (Fig.
14a). Evidentemente, aparecerá una corriente de colector que, en el punto de operación, será IOU T =
hF E · IB a la que habría que añadir una perturbación asociada a la fuente en pequeña señal. Al
pasar a pequeña señal, el colector estaría unido a tierra y la fuente de polarización, IB , desaparece.
w
/
w
w
id
e
rs
iv
Pa
ra
u
so
paralelo una fuente de corriente sinusoidal de pequeña señal y de frecuencia variable,
:/
U
n
De este modo, se obtiene el circuito de Fig. 14b.
tt
p
Nuestro objetivo es, en primer lugar, determinar la relación entre las dos corrientes en pequeña
h
señal, iout/iin . Para agilizar el cálculo, hagamos una serie de puntualizaciones:
vbe está determinada por la corriente de entrada y un paralelo de dos condensadores,
Cπ y Cµ , y una conductancia, gπ . En general, los transistores bipolares tienen una capacidad
de difusión mucho mayor que la de unión. Por ello, vamos a despreciar Cµ . En muchos textos,
1. La tensión
este paso se hace a posteriori pero, por comodidad, nosotros lo vamos a hacer ahora.
2. En el paralelo formado por
Electrónica Analógica
gπ
y
Cπ
podemos intuir que la primera será despreciable a altas
Ingeniería Superior en Electrónica
23
Modelos en pequeña señal
Tema 2
frecuencias, que es donde está la frecuencia de transición. En consecuencia,
vbe ≈
iin
Cπ ·s
(27)
go no circula corriente al estar sus extremos cortocircuitados a
tierra. Por ello, la corriente iout será, simplemente, el valor de la fuente de corriente pues
suponemos que la fuga a través de Cµ es despreciable. Por tanto:
3. A través de la conductancia
fT ,
(28)
como aquélla en la que la ganancia en corriente tiene
d
ri
Se dene la frecuencia de transición,
iin
iout
gm
⇒
=
Cπ ·s
iin
Cπ ·s
d
iout = gm ·vbe = gm ·
M
a
módulo 1. En otras palabras:
7
5 · 10−10
alu
m
a
d
n
os
torno a 3.2 GHz.
s. En consecuencia, podemos situar su máxima frecuencia de trabajo en
p
es del orden de
c
m
o
El transistor MOSFET
C
4.
(29)
es el tiempo medio de tránsito. En un transistor como el 2N2222, dicho parámetro
m
τF
de
Donde
1 gm
1 1
·
=
·
2·π Cπ
2·π τF
la
fT =
lu
.e
te
s
n
se
Aplicando Eq. 25:
d
e
gm gm gm
=
Cπ ·sT Cπ ·ωT = 1 ⇒ ωT = 2·π·fT = Cπ
.u
de
En comparación con el transistor bipolar, el transistor MOSFET es muy fácilmente describible
w
id
so
en pequeña señal. El motivo es que, a pesar de tener tres terminales, uno se comporta como un
w
w
e
rs
Pa
ra
u
abierto por lo que solo puede circular corriente entre drenador y fuente. Ciertamente, veremos que
a frecuencias elevadas hay corriente a través de la puerta pero, en primera instancia, puede obviarse
/
iv
la existencia de estas corrientes.
:/
n
Asimismo, en electrónica analógica, solo nos interesan los transistores MOSFET en saturación.
tt
p
U
Carecen de interés tanto la zona de corte como la zona óhmica. Este hecho simplica aún más las
cosas. Por otra parte, veremos que el modelo en pequeña señal es válido tanto para NMOS como
h
para PMOS recordando, claro está, que el drenador y la fuente de ambos transistores se habrán
8
intercambiado .
7 No es sino el parámetro TF del modelo SPICE.
8 Insistiendo: En un NMOS, la fuente está abajo y en un PMOS, arriba.
Electrónica Analógica
Ingeniería Superior en Electrónica
24
Modelos en pequeña señal
Tema 2
4.1.
Modelo básico a bajas frecuencias
A bajas frecuencias, y suponiendo que trabajamos con tecnologías de longitud de canal del orden
del micrómetro, podemos describir las características DC de un transistor MOS en saturación como:


IG = 0
(30)
 I = β· (V − V )2 · (1 + λ·V )
DS
GS
TH
DS
Siendo
β
un parámetro que depende de la movilidad de los portadores y de las dimensiones del
VT H ,
d
canal. Se ha supuesto que el transistor es de canal N. Esto implica que la tensión umbral,
VSB
según la expresión:
γ
y
9
son parámetros tecnológicos independientes de las tensiones aplicadas . Uti-
∆XY ≡ xY ,
se puede demostrar que:
iG = 0
∂IDS ∂IDS ∂VT H +
·vDS +
·
·vSB
∂VDS Q
∂VT H Q ∂VSB Q
la
lizando la notación típica
d
VT H,0 , φ
(31)
lu
.e
te
s
n
se
donde
p
p φ + VSB − φ
e
VT H = VT H,0 + γ·
M
a
entre sustrato y fuente,
d
ri
es positiva. Recordemos que, por efecto sustrato, esta tensión depende de la diferencia de tensión
de
∂IDS ·vGS
=
∂VGS Q
(32)
p
m
alu
m
a
d
n
os
iDS
En el último término de esta expresión, hemos aplicado la regla de la cadena para estudiar la inuencia
c
m
Asimismo, recordemos que el sujo Q indica, simplemente, que las derivadas se calculan
o
vSB .
C
de
con los valores de tensiones y corrientes del punto de operación. Estudiamos ahora la estructura de
.u
de
esta ecuación. Cada término tiene dimensiones de corriente y, en teoría de circuitos, una corriente
w
id
so
igual a la suma de varias corrientes equivale a un conjunto de elementos en paralelo. De esos tres
w
w
e
rs
Pa
ra
u
elementos en paralelo, hay uno que relaciona
vDS
con
iDS .
Esto no es sino la ley que gobierna una
resistencia (o conductancia) entre los nudos D y S. Esta conductancia se va a denominar
gO
Los
y, la segunda,
tt
p
:/
gm
gmb .
Así, Eq. 32 se transformaría en:
iDS = gm ·vGS + gO · vDS + gmb ·vSB
(33)
h
U
n
importante, se llamará
/
iv
otros dos solo pueden ser fuentes de corriente controladas por tensión. La primera, que es la más
Fig. 15 esboza como sería el equivalente circuital de un transistor MOS deducido a partir de esta
ecuación. Ahora, la pregunta pertinente es saber cuanto vale cada uno de los parámetros. Vayamos
uno a uno:
9 Consultar la descripción del modelo SPICE del MOS o la bibliografía de la asignatura para conocer sus signicados.
Electrónica Analógica
Ingeniería Superior en Electrónica
25
Modelos en pequeña señal
Tema 2
Figura 15: Equivalente básico en pequeña señal de un transisto MOS.
gO :
d
1.
donde
(34)
M
a
d
ri
∂IDS ∂ (1 + λ·VDS )
= λ·β· (VGS − VT H )2 ≈ λ·IDS,Q
gO =
= β· (VGS − VT H )2 ·
∂VDS Q
∂VDS
IDS,Q
es la corriente de drenador a fuente (o viceversa en PMOS) en el punto de
gm :
lu
.e
te
s
n
se
2.
d
e
operación.
de
la
s
p p
∂IDS IDS,Q
gm =
β· IDS,Q
=
2·β·
(V
−
V
)
·
(1
+
λ·V
)
≈
2·β·
≈
2·
GS
T
H
DS
∂VGS Q
β
(35)
p
m
:/
/
e
rs
∂VT H γ
p
=
∂VSB Q 2· φ + VSB,Q
γ
gmb = −gm · p
2· φ + VSB,Q
tt
p
U
n
Por lo que:
w
id
so
iv
Pa
ra
u
y que, por otro lado,
.u
∂IDS = −2·β· (VGS − VT H ) · (1 + λ·VDS ) ≈ −gm
∂VT H Q
de
que:
c
m
o
En este caso, la expresión es algo más compleja. En primer lugar, se puede demostrar
C
gmb :
w
w
3.
gm .
alu
m
a
d
n
sencilla de
os
En este caso, se ha despreciado el efecto de modulación del canal para obtener una expresión
(36)
h
El hecho de que este parámetro sea negativo nos obliga a redenir la tensión de referencia.
Así, podemos considerar
gmb
como un término positivo si multiplica a
vBS
en lugar de
vSB ,
como se había propuesto originalmente. Esta corrección ya se ha incorporado a Fig. 15. En
general,
gmb
vale, aproximadamente,
(0,1 − 0,3) · gm
en la mayor parte de los transistores.
Por otra parte, ocurre que, en la mayoría de los casos, el sustrato está conectado a una tensión
constante de modo que
vBS
equivale a
−vS .
Por ello, el circuito de Fig. 15 se transforma en el de
Fig. 16. Asimismo, en los transistores discretos, se rompe la simetría entre drenador y fuente pues
Electrónica Analógica
Ingeniería Superior en Electrónica
26
Modelos en pequeña señal
Tema 2
Figura 16: Equivalente básico en pequeña señal de un transisto MOS suponiendo tensión de sustrato
constante.
y no tiene
M
a
d
ri
gmb .
sentido hablar de la transconductancia
VSB = 0
d
el sustrato se cortocircuita con la fuente con lo que, a partir de ese momento
4.2.
Parásitos en un transistor MOS. Capacidades parásitas.
e
Hay tres tipos de parásitos en un transistor MOS. En primer lugar, y como suele ocurrir en
d
cualquier dispositivo electrónico, existen resistencias parásitas en serie con cada uno de los términales.
lu
.e
te
s
n
se
Evidentemente, hay que descartar la resistencia parásita de puerta por inútil ya que estaría en serie
RD
RS .
y
Estas resistencias desempeñan un papel importante cuando el transistor es
de
y fuente,
la
con un condensador. Sin embargo, sí pueden tener importancia las resistencias parásitas de drenador
os
CMOS.
p
atravesado por corrientes considerables como, por ejemplo, en las etapas de salida de los dispositivos
m
alu
m
a
d
n
Otra familia de parásitos de importancia son las uniones PN inversamente polarizadas que existen
c
m
o
entre drenador/fuente y sustrato. Su modelado es sencillo pues solo hay que conectar cada terminal
CJDB ).
gDB )
y un par de capacidades de unión,
Son equivalentes a las estudiadas en el Apartado 2.2.
.u
de
(CJSB y
C
con el paralelo de una conductancia muy pequeña (gSB y
w
id
so
Mayor importancia tienen los condensadores parásitos asociados al óxido de puerta. Así, en un
w
w
e
rs
Pa
ra
u
transistor MOS, pueden aparecer capacidades parásitas entre la puerta y la fuente (CGS ), el drenador
(CGD ) y el sustrato (CGB ). En un transistor en saturación, la capacidad con mayor importancia
:/
iv
n
CGS
es prácticamente igual a la capacidad total del óxido de puerta,
/
CGS , cuyo valor
≈ CG = COX · W · L.
es la primera,
tt
p
U
Fig. 17 muestra el modelo en pequeña señal de un transistor MOS incluyendo todos los parásitos
que se han descrito en este apartado. Por otra parte, los transistores MOS discretos carecen de
h
sustrato pues éste se encuentra cortocirtuitado a la fuente. Por ello, el modelo original en pequeña
señal se convierte en el de Fig. 18. Puede apreciarse que aparece una capacidad parásita entre
drenador y fuente que puede afectar fuertemente al comportamiento en frecuencia del dispositivo.
4.3.
Frecuencia de transición
A semejanza del transistor bipolar, puede denirse un parámetro, llamado frecuencia de transición , que determina el buen comportamiento de un transistor MOS en el dominio de la frecuencia.
Electrónica Analógica
Ingeniería Superior en Electrónica
27
Modelos en pequeña señal
d
e
M
a
d
ri
d
Tema 2
p
.u
c
m
m
o
w
:/
/
w
w
id
e
rs
tt
p
h
U
n
iv
Pa
ra
u
so
de
C
alu
m
a
d
n
os
de
la
lu
.e
te
s
n
se
Figura 17: Equivalente en pequeña señal de un transistor incluyendo parásitos.
Figura 18: Equivalente en pequeña señal de un transistor incluyendo parásitos.
Electrónica Analógica
Ingeniería Superior en Electrónica
28
Modelos en pequeña señal
Tema 2
de
la
lu
.e
te
s
n
se
d
e
M
a
d
ri
d
Figura 19: Polarización de un transistor NMOS para calcular su frecuencia de transición.
m
alu
m
a
d
n
os
transición.
p
Figura 20: Equivalente en pequeña señal de un transistor NMOS para calcular su frecuencia de
c
m
o
Para ello, debemos suponer que el transistor se encuentra polarizado en saturación y que excitamos
C
en pequeña señal con una fuente de corriente. Este estímulo provoca una variación en la corriente de
.u
de
salida (Fig. 19). Evidentemente, se plantea una dicultad intrínseca de diseño pues ¾cómo se puede
w
id
so
polarizar en DC un transistor MOS atacando la puerta con una fuente de corriente? Sin embargo,
w
w
e
rs
Pa
ra
u
recordemos que esto es un experimento mental.
En pequeña señal, ese circuito se convierte en el de Fig. 20. En esta estructura, gran parte de
/
iv
los elementos pasivos están cortocircuitados por lo que, tras eliminar estos elementos, obtendríamos
:/
tt
p
vGS =
s· (CGS
iIN
iIN
≈
+ CGB + CGD )
s·CGS
(37)
h
U
n
el circuito de Fig. 21. Operando en este circuito, se puede deducir que:
Ocurre que, en general, suele predominar
CGS
sobre las otras capacidades por lo que se ha podido
realizar esta simplicación. Por otro lado, si despreciamos la corriente que uye a través de
iO = gm ·vGS =
En la frecuencia de transición,
Electrónica Analógica
fT
gm
iO
gm 1
·iIN ⇒
=
·
s·CGS
iIN
CGS s
CGD :
(38)
el módulo de esta ganancia debe hacerse 1. Esto solo es posible
Ingeniería Superior en Electrónica
29
Modelos en pequeña señal
Tema 2
si:
√
IDS
(39)
por lo que la frecuencia de transición aumenta
e
gm ∝
M
a
gm
CGS
fT =
Dos hechos importantes. En primer lugar,
d
ri
d
Figura 21: Simplicación del circuito de Fig. 20.
d
con la corriente de polarización del dispositivo. Esto constituye una diferencia clara con el transistor
lu
.e
te
s
n
se
bipolar, en el que la frecuencia de transición dependía solo de un parámetro tecnológico. Por otra
la
parte, suponiendo constantes las tensiones de polarización de los transistores:
(40)
p
de
2·0,5·µX · W
· (VGS − VT H )
2·β· (VGS − VT H )
1
gm
L
=
=
∝ 2
CGS
CGS
W ·L·COX
L
os
fT =
m
alu
m
a
d
n
En conclusión, cuanto menor sea la longitud efectiva del canal, mayor es la frecuencia de transición.
o
Así, un progreso tecnológico que haga que reduzca a la mitad la escala de integración de un proceso
c
m
C
CMOS implica que la frecuencia de transición se cuadriplica. Asimismo, Eq. 40 también nos señala
VGS ,
mayor es la frecuencia de transición. Este
.u
de
que, cuanto mayor sea la tensión de puerta-fuente,
w
so
parámetro está de algún modo relacionado con la tensión de alimentación lo cual nos hace intuir
w
w
id
Pa
ra
u
que cuanto menores sean las tensiones de alimentación, peor comportamiento en frecuencia tienen
/
iv
:/
tt
p
n
El transistor JFET
U
5.
e
rs
los dispositivos, hecho que se observa de forma habitual.
La descripción del transistor JFET en pequeña señal es trivial una vez explicado el transistor
h
MOS. La razón de ello es que, en saturación, la ecuación que rige el comportamiento de un JFET es
similar a Eq. 30, con la salvedad de que en lugar de hablar de la tensión umbral,
a la tensión de pinch-o,
VP .
VT H ,
se menciona
Además, esta última tensión es constante para cada dispositivo pues
no hay efecto sustrato. En consecuencia, el modelo básico en pequeña señal de un JFET se reduce
a una transconductancia,
gm ,
y una conductancia,
go ,
y no hay ni rastro de
gmb .
Fig. 22 muestra en
qué se convierte un transistor JFET, sea cual sea el tipo de canal.
Electrónica Analógica
Ingeniería Superior en Electrónica
30
Modelos en pequeña señal
Tema 2
e
M
a
d
ri
d
Figura 22: Equivalente básico en pequeña señal de un transistor JFET.
lu
.e
te
s
n
se
d
Figura 23: Equivalente en pequeña señal con parásitos de un transistor JFET.
de
la
Los valores de los parámetros del modelo en pequeña señal serían:
s
p p
IDS,Q
≈ 2· β· IDS,Q
β
(41)
p
m
alu
m
a
d
n
os
gm = 2·β· (VGS − VP ) · (1 + λ·VDS ) ≈ 2·β·
c
m
C
o
gO = λ·β· (VGS − VP )2 ≈ λ·IDS,Q
(42)
Los parásitos que pueden aparecer en este circuitos son bastante sencillos (Fig. 23). En primer lugar,
.u
de
aparecerán resistencias parásitas en el drenador y la fuente (RD y
RS ).
También aparecen capaci-
w
id
so
dades parásitas entre la puerta y los terminales del canal, ambas de tipo unión PN en inversa. Ocurre
w
w
e
rs
Pa
ra
u
que, en general, se supone por simplicidad que el efecto capacitivo se distribuye equitativamente
entre ambos terminales. En otras palabras,
CJGS = CJGD = 21 CJG
donde
CJG
es la capacidad de
/
iv
unión entre puerta y canal completo.
:/
CGS
por su equiv-
Así, la frecuencia de transición sería:
tt
p
CJG 10 .
fT =
h
U
alente,
n
¾Cual es la frecuencia de transición? Podremos utilizar Eq. 39 reemplazando
gm
CJG
(43)
Los resultados cualitativos serían similares. Se puede demostrar, por ejemplo, que la frecuencia de
transición aumenta linealmente con
√
IDS
y con
L−2 ,
siendo
L
la longitud del canal del transistor.
La dependencia con la tensión de puerta-fuente es más compleja al no ser
CJG
constante. Por ello,
no se discutirá el caso.
10 O, más concretamente, hemos reemplazado
CJG
CGS + CGD + CGB
por la capacidad total de la puerta de un JFET,
en Eq. 37.
Electrónica Analógica
Ingeniería Superior en Electrónica
31